基于全體圈個數為4的LFSR 構造de Bruijn 序列的研究

周琮偉，胡斌，關杰

（信息工程大學密碼工程學院，河南 鄭州 450001）

0 引言

近幾十年來，線性反饋移位寄存器（LFSR,linear feedback shift register）序列被廣泛應用于通信編碼和密碼算法中，例如眾所周知的m序列。然而由于LFSR固有的線性制約性及輸入的多條亂源序列存在時間差，可以對其經過非線性改造產生的密鑰流的序列周期與線性復雜度進行深刻的代數刻畫[1]，并且在此基礎上提出的相關攻擊[2]、最佳仿射線性攻擊[3]與代數攻擊[4]等分析方法均有對應的算法攻擊實例，因此逐漸將研究對象從LFSR 轉向非線性反饋移位寄存器序列。其中n級de Bruijn 序列是一類重要的非線性反饋移位寄存器序列，其圈結構中圈長達到最大周期2n，同時其偽隨機性質與線性復雜度[5]均優于m序列。此外，de Bruijn 序列在衛星通信[6]、電網技術[7]和基因測序[8]中均有廣泛應用。

構造de Bruijn序列一直以來都是研究de Bruijn序列的核心問題，其構造思路主要是基于反饋移位寄存器圈結構中各圈的合并，其難點在于研究各圈上的共軛狀態分布。在20 世紀70 年代至90 年代，國際上掀起了研究構造de Bruijn 序列的熱潮，各種算法和結果層出不窮[9-17]，其中文獻[12]比較全面地介紹了de Bruijn 序列構造的經典算法。近期國內學者也給出了一些構造算法[18-19]，但快速構造密碼學性質良好和實用性強的de Bruijn 序列特征函數仍然是一個長期亟待解決的問題。

從20 世紀70 年代起，Lempel[20]引入D-同態的概念，利用n級de Bruijn 序列在D-同態下的原像是2 個n+1級的等長圈，并結合2 個等長圈上共軛狀態的分布特點，給出了一個由n級到n+1級de Bruijn 序列特征函數的遞歸構造方法，且可以進一步拓展到n+2級[21]。此類遞歸思路實際上可以看作產生n級de Bruijn 序列的非線性反饋移位寄存器級聯小級數的LFSR，Chang 等[22]利用線性方程的方法給出了較為清晰的代數表達式。

另一方面，Li 等[23-25]、Li 等[26-27]和Chang 等[28]研究了幾類級聯型LFSR的特征多項式，給出了其中幾個n級LFSR 圈結構的因子關聯圖，從而給出了其構造的算法和計數。特別地，Dong 等[29]還研究了利用仿射反饋移位寄存器構造de Bruijn 序列的方法。以上方法均建立在小級數的LFSR 級聯特征多項式為本原多項式的LFSR。同時，Dong 等[30-31]還研究了周期為的n次不可約多項式為特征多項式的LFSR 圈結構的因子關聯圖，證明了其特征多項式的鄰接矩陣（因子關聯圖的矩陣化）與本原多項式的k?鄰接矩陣相等，并利用雅可比和給出了k=3,5時其對應的k?鄰接矩陣元素的具體表達式，即從理論上給出了這類de Bruijn 序列的計數。從構造的實用性角度上分析，通過并圈方式直接構造的de Bruijn 序列特征函數基于的LFSR 圈結構中圈個數越少，效率一般越高。由于LFSR 圈結構中圈個數一定為偶數[17]，且等于2的情形為m序列中添加一個零，因此本文進一步研究基于圈個數為4的LFSR 構造de Bruijn 序列的方法。同時，為了拓寬上述研究所基于的LFSR 種類，增加構造的de Bruijn 序列數目，給出更多清晰的de Bruijn 序列特征函數形式，本文的工作延續和拓展了上述文獻中的構造方法，并結合文獻[31]的相關結論，提出了基于全體圈個數為4的LFSR 構造de Bruijn 序列的方法。

1 一類級聯型的反饋移位寄存器的圈結構

由于非奇異反饋移位寄存器產生的輸出序列都是周期的，因此可以在此基礎上定義序列的左移變換為

為Ω(f)的一個平移等價類或者一個圈。若Ω(f)有r個圈，則Ω(f)或反饋移位寄存器的圈結構可以寫作

引理1 表述了圈結構中非常重要的圈合并與圈分解的概念。

引理1[32]設ν=(v0,v1,…,vn?1)在圈[si]上，其共軛狀態=(v0⊕ 1,v1,…,vn?1)在圈[sj](j≠i)上，則可以通過交換ν和ν?這2 個狀態的后繼使這2 個圈合并為一個圈，其對應的圈合并后的特征函數為

同理，若ν和其共軛狀態都在圈[si]上，則可以通過交換ν和這2 個狀態的后繼使這一個圈分解為2 個圈，其對應的圈分解后的特征函數也如上。

級聯或者稱為反饋移位寄存器的串聯始見于文獻[33]，由定義1 描述。

定義1設n級的反饋移位寄存器在初態(a0,a1,…,an?1)下產生序列a且特征函數為f，m級的反饋移位寄存器初態為 (b0,b1,…,bm?1)且特征函數為g，則稱特征函數為f?g的反饋移位寄存器為級聯型，其輸出序列b滿足

特征函數f?g對應的m+n級的級聯型反饋移位寄存器的結構框架如圖1 所示。

圖1 特征函數f ? g對應的m +n級的級聯型反饋移位寄存器的結構框架

為了研究基于LFSR的反饋移位寄存器的級聯特征，本文首先給出LFSR 特征多項式的相關概念。設全體LFSR的特征函數形如

則存在F2上的一一映射

此時，稱ψ(x)為該LFSR的特征多項式。文獻[17]指出，若ψ(x)為F2上的n次不可約多項式，則該LFSR的圈結構Ω(ψ(x))可表示為

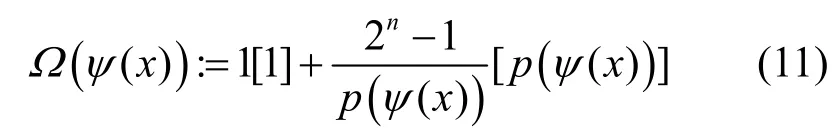
其中，? [ ?]表示圈長為?的圈有?個，p(ψ(x))表示ψ(x)在F2上的周期。因此，如果可以將F2上的任一特征多項式分解為若干不可約多項式的乘積[17]，則可以確定LFSR的圈結構。文獻[34]證明了包含LFSR的一類級聯型反饋移位寄存器的輸出序列的周期分布情況，即引理2。

引理2[34]設g(x0,x1,…,xm)是LFSR的特征函數，其特征多項式ψ(g)為F2上的m次不可約多項式，且設

其中，序列a的周期表示為p(a)。

1) 若p(ψ(g))/|p(a)，設在初 態 (a0,a1,…,an?1)加載下，特征函數為f?g的級聯型的反饋移位寄存器生成的序列集合為θ(g)?1(a)，則θ(g)?1(a)包含一條周期長度為p(a)的序列和2m? 1條周期長度為 lcm {p(a),p(ψ(g))}的序列，其中lcm{p(a),p(ψ(g))}表示p(ψ(g)),p(a)的最小公倍數。

通常，基于級聯型反饋移位寄存器構造de Bruijn序列的方法主要是將給定的特征函數依據引理2的1)中的限制條件代入級聯型的遞歸式，并直接對集合θ(g)?1(a)中的生成序列按平移等價進行分類，便可推導出其圈結構中的圈個數，即定理1，從而進一步得到這類級聯型反饋移位寄存器的圈結構Ω(f?g)。

均與B′平移等價，且僅限于取它們作為初態時所得序列。注意到，B′的周期為q=Pp(a)，因此

只有前P個兩兩不同的數組作為初值產生的序列與B′平移等價。根據上面的討論，所有平移等價的序列在同一個圈上，因此共有

個周期為q的圈，加上一個周期為p(a)的圈。證畢。

若Ω(f)中的每個圈圈長都不被p(ψ(g))整除，將Ω(f)中所有平移不等價的序列代入定理1，可以立即推出這類級聯型反饋移位寄存器的圈結構，即推論1。

推論1 設g(x0,x1,…,xm)是LFSR的特征函數，其特征多項式ψ(g)為F2上的m次不可約多項式，設

2 構造de Bruijn 序列的方法

利用f?g的特征函數結構，可以給出任意n級LFSR 與級聯型反饋移位寄存器之間的關系。

定理2任意n級LFSR 等價于唯一確定的若干LFSR 經過級聯生成的級聯型反饋移位寄存器。

證明設n級LFSR的特征函數為

代入式(29)可得h(x) ?g(x) =f(x)，即特征函數為h(x)和g(x)對應的LFSR 級聯生成的級聯型反饋移位寄存器恰為特征函數為f(x)對應的LFSR。進一步地，對于ψ(f(x))分解為一般情況時，本文可以反復迭代上述過程，又根據多項式的唯一分解定理，因此任意LFSR 均等價于唯一確定的若干LFSR經過級聯生成的級聯型反饋移位寄存器，此時其特征多項式分解的若干不可約多項式恰為級聯型反饋移位寄存器中各LFSR的特征多項式。證畢。

根據定理2 以及推論1，由于LFSR 圈結構中圈個數至少為2，則對于任意圈個數為4的n級LFSR 等價的級聯型反饋移位寄存器，級聯的LFSR個數最多為2，因此可得定理3。

定理3圈個數為4的n(n≥ 3)級LFSR 個數為

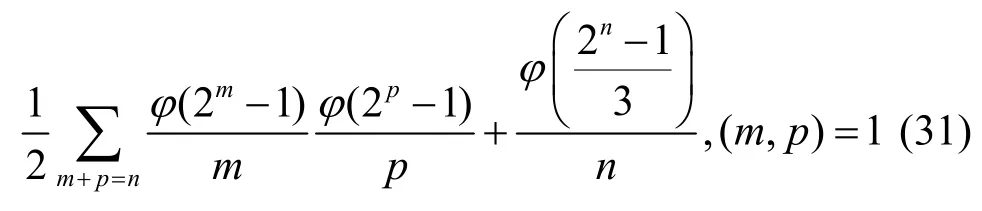
其中，φ為歐拉函數，當x不為整數時，φ(x)=0。

證明定理2 中，對于任意n級LFSR的特征函數

本文要求其為非奇異，即c0=1。當n=1時，ψ(f(x))只能取1⊕x，故其圈結構為

當n>1時，由于ψ(f(x))可以分解為若干不可約多項式的乘積，而這些不可約多項式恰好對應級聯型反饋移位寄存器中各LFSR的特征多項式，當特征多項式為不可約多項式ψ(x)時，其圈結構可表示為

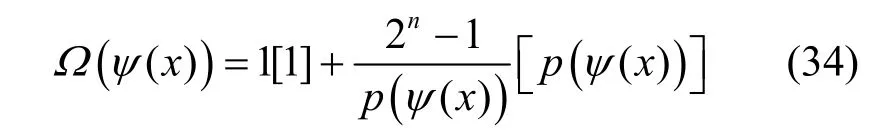
綜上，當n為任意正整數時，其分解的不可約多項式對應的LFSR 圈結構中圈個數至少為2。根據推論1，若分解的不可約多項式超過2 個，則圈個數超過4，故分解的不可約多項式至多為2 個。

當ψ(f(x))為不可約多項式時，可得

根據文獻[35]，F2上周期為l的n次不可約多項式的個數為在此情形下，其圈個數為4的LFSR 個數為

當ψ(f(x))分解為2 個不可約多項式的乘積時，分別設這2 個不可約多項式為

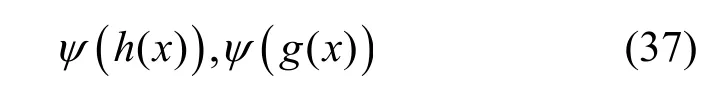
且滿足ψ(f(x))=ψ(h(x))ψ(g(x))，其級數為m,p且m+p=n，根據推論1，不可約多項式對應的LFSR 圈結構中圈個數只能為2，故此時這2 個不可約多項式即本原多項式，又根據輾轉相除法，當且僅當(m,p)=1時，有

此時，圈個數恰為4。注意到，當h和g均為線性情形時，Ω(h?g)=Ω(g?h)，在此情形下，其圈個數為4的LFSR 個數為

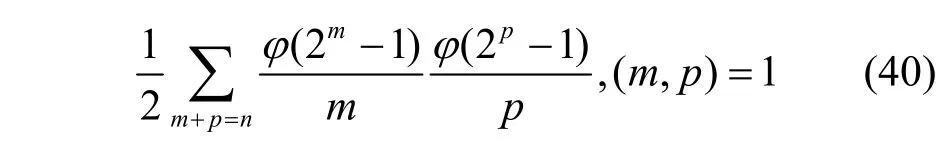
綜上，本文要求n≥ 3是因為m和p不能同時為1，當n=3時，唯一一個圈個數為4的LFSR的特征函數為x0⊕x3。2 種情形的個數加之，定理3 即證。證畢。

文獻[31]證明了定理3 中當ψ(f(x))為不可約多項式時，通過圈合并的方法可得到的de Bruijn 序列個數為

定理4設任意m級和p級LFSR的特征函數分別為的級聯型反饋移位寄存器產生de Bruijn 序列。且產生周期為2m+p的de Bruijn 序列個數為

證明根據定理3 可知，當(m,p)=1時，Ω(h?g)中的圈個數為 4，故可設對應的圈為{0,b1,b2,b1+b2}。由于a1,a2是m序列，故圈b1,b2上的狀態均不可能是共軛的。下證圈b1,b2之間只有一對共軛狀態，設 (x0,x1,…,xm+p?1)在b1上，(x0⊕ 1,x1,…,xm+p?1)在b2上，則滿足

圖2 4 個圈之間的共軛狀態分布

使這4 個圈合并的方式共有2 種。

2) 先合并圈b1,b2，然后合并b1+b2，最后合并0。

這2 種方式產生de Bruijn 序列的特征函數分別為

接下來固定h,g，判定這2 種方式產生de Bruijn 序列的個數。

針對方式1)，本文假設存在一組(k′,l′)，滿足則可得判定式

同理，針對方式2)，由于只有唯一的小項需要比較，故此方式產生的de Bruijn 序列個數為

綜上，固定h,g之后，這4 個圈合并產生de Bruijn 序列的個數為2m+p? 2。下證當h,g變化時，只針對方式1)判定是否有重復的特征函數，而方式2)顯然沒有。

設ψ(h′)和ψ(g′)分別是m′和p′次本原多項式，且有m+p=n=m′+p′，設針對方式1)產生de Bruijn 序列的特征函數為

綜上，結合這4 個圈合并產生de Bruijn 序列的個數為2m+p? 2可知，由定理4 描述的特征函數產生de Bruijn 序列的個數為

證畢。

由定理4 可知，當圈個數為4的LFSR的特征多項式分解為2 個不可約多項式的情形時，只能通過定理中描述的這幾種并圈方式構造de Bruijn 序列的特征函數。結合定理3 與文獻[31]的相關結論，本文證明了基于全體圈個數為4的n級LFSR 構造n級de Bruijn 序列的全部數目。定理4 證明過程中，只要求解出n元線性方程組的解，通過任意2 個互素的m,p(m+p=n)級本原多項式，就可以直接得到定理4 中沒有重復的且數量龐大的n級de Bruijn序列特征函數。

3 結束語

本文從圈個數的角度，基于LFSR的反饋移位寄存器的級聯特征和線性方程的思想，給出了圈個數為4的LFSR的具體數目，從而給出了基于全體圈個數為4的n級LFSR 構造n級de Bruijn 序列的并圈方法，并且得到了其全部數目。該方法可以通過任意2 個級數互素的本原多項式直接構造大級數的de Bruijn 序列特征函數，同時其分析思路也可以進一步豐富和促進LFSR 構造de Bruijn 序列的理論結果。但該方法仍然需要求解一個n元線性方程組，因此在該方法上是否有更具體的de Bruijn 序列特征函數形式，以及在圈個數上是否可以進一步推廣將是筆者下一步研究的內容。