工件分特征下的五軸數控機床關鍵幾何誤差分析與補償方法

盧成偉 錢博增 王慧敏 項四通

寧波大學機械工程與力學學院，寧波，315211

0 引言

五軸數控機床靈活性好、生產效率高，在制造業中發揮著重要作用，廣泛應用于汽車制造、航空航天等領域。幾何誤差是數控機床在制造與裝配過程中引起的不可避免的偏差，嚴重影響機床的加工精度，但具有重復性好、長時間內穩定的特點[1]，故補償幾何誤差已成為較為實用與可行的提高機床整體加工精度的方法之一。然而五軸機床的幾何誤差多達41項[2]，補償所有的幾何誤差工作量大，因此辨識并補償影響機床加工精度的關鍵幾何誤差具有重要意義。

靈敏度分析可有效地確定輸入參數變化對輸出結果影響的關鍵性[3]，該方法已成為量化幾何誤差對機床加工精度的影響和辨識關鍵誤差的有效途徑。常見的靈敏度分析方法可分為局部靈敏度分析和全局靈敏度分析兩種[4]。局部靈敏度分析亦稱“一次變化法”，此種方法僅檢驗一個參數，其他參數取中心值，評價輸出結果在該參數變化時的變化量，如偏微分運算法[5-7]。全局靈敏度分析檢驗多個參數同時變化及參數之間的相互作用對輸出結果的影響，其結果受多個輸入參數的影響，常見方法有Sobol法[8]、Morris法[9]和積分法[10]等。

近些年來，國內外學者基于靈敏度分析方法對機床幾何誤差展開了大量研究。LI等[11]考慮刀具的位置和姿態，分別使用全局和局部靈敏度對BC雙擺頭五軸機床進行了分析，研究發現幾何誤差中的角度誤差對機床加工精度的影響較大。劉奕穎等[12]以機床裝配階段中的幾何誤差為出發點，基于靈敏度分析方法對精密臥式鏜床的運動軸進行公差設計。GUO等[13]引入全局定量靈敏度分析，充分考慮機床工作空間幾何誤差的概率分布，直觀地描述了幾何誤差分量對位置和方向誤差矢量的影響，確定了各幾何誤差對機床精度的影響。FU等[14]發現不同軸對機床精度的影響因其在機床結構中的位置及其局部誤差而異，提出了機床各運動軸的幾何誤差貢獻建模和靈敏度評估方法，獲得了各軸的幾何誤差對機床加工精度的影響，并確定了機床的關鍵運動軸。ZHANG等[15]基于Sobol法與遺傳算法對三軸立式銑床的全局靈敏度進行了分析，并采用乘法降維法來簡化計算。楊赟等[16]基于靈敏度分析得出的關鍵幾何誤差，提出了一種批量化建模和補償方法，對一批相同類型的三軸立式加工中心進行了批量誤差補償，提高了機床精度。上述研究在靈敏度分析中雖然取得了一定的成果，但大多數研究主要關注幾何誤差對機床體積誤差的敏感性，而對工件形狀誤差的敏感性討論較少。

面向復雜工件的形狀誤差，學者們亦開展了靈敏度分析研究。LI等[17]使用靈敏度分析方法確定了軌跡對誤差運動的敏感性，并通過加工ISO 10791-7-M3試件及S形試件進行了驗證。XIA等[18]建立了幾何誤差與齒面位姿誤差之間的映射模型，基于全局靈敏度分析確定了影響齒廓和螺旋偏差的關鍵幾何誤差，從而簡化了誤差補償表達式并提高了齒輪加工精度。YAO等[19]建立了考慮幾何誤差的超精密金剛石車削中心的運動學誤差模型，通過靈敏度分析得出了影響加工精度的關鍵誤差，并提出了一種減小或消除相應機械系統定位誤差的對準方法，從而提高了被加工曲面的成形精度。上述研究通過靈敏度分析確定了影響工件整體加工精度的關鍵幾何誤差。然而五軸加工中，復雜工件通常由多個典型特征組成，且各特征受幾何誤差的影響程度不同，因此對工件整體進行靈敏度分析的效果不如分特征分析。

針對上述問題，本文提出了一種工件分特征下的五軸數控機床關鍵幾何誤差分析與補償方法。將工件特征分解為平面、斜面、圓柱和圓錐臺等典型特征，基于靈敏度分析分別辨識出各典型特征對應的關鍵幾何誤差。最后，通過對辨識出的關鍵幾何誤差進行補償，有效地提高了工件的加工精度。

1 誤差模型的建立

1.1 機床的體積誤差模型

圖1a為AC雙轉臺五軸機床的結構示意圖，該機床包含X/Y/Z三個平動軸以及A/C兩個旋轉軸。本文依據多體系統理論和齊次坐標變換建立了機床的體積誤差模型。該機床的運動鏈為WCAMXYZT型，具有圖1b所示的運動鏈結構與連接關系。A軸和C軸屬于工件運動鏈，X軸、Y軸和Z軸屬于刀具運動鏈，運動鏈遵循“WCS→CCS→ACS→MCS→XCS→YCS→ZCS→SCS→TCS”的傳遞順序。其中，WCS表示工件坐標系，ACS、CCS、XCS、YCS、ZCS分別表示A軸、C軸、X軸、Y軸和Z軸的坐標系，MCS表示機床坐標系，SCS表示主軸坐標系，TCS表示刀具坐標系。

(a)AC雙轉臺五軸機床結構示意圖

在該機床運動鏈鏈中，主要涉及5個運動部件——X/Y/Z/A/C軸，共有41項幾何誤差，其中有30項與位置有關的誤差(PDGEs)，11項與位置無關的誤差(PIGEs)，如表1所示。旋轉軸誤差的定義參照ISO 230-7—2006[20]。表1中，δ為線性誤差，ε為角度誤差，S為垂直度誤差。

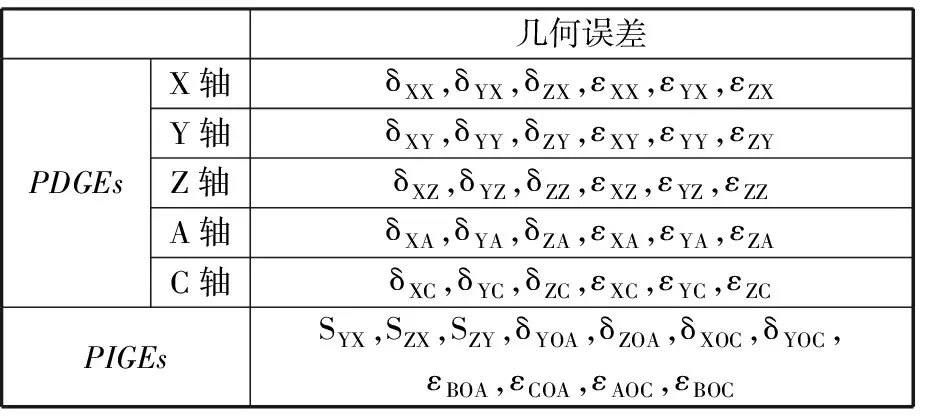
表1 AC雙轉臺五軸數控機床的幾何誤差列表

在機床實際的運動過程中，由于存在幾何誤差的影響，刀具的實際切削點相對于工件的空間位置會存在一定的偏差(即機床的體積誤差ΔE)，可由下式計算得到：

(1)

1.2 機床幾何誤差建模

本實驗中使用激光干涉儀和電子水準儀逐項測量X/Y/Z平動軸的幾何誤差，利用球桿儀間接測量A/C旋轉軸的幾何誤差，并擬合為位置的三次多項式函數。X軸的6項幾何誤差模型的表達式如下：

(2)

其中，x為機床X軸的絕對運動量，m；δXX、δYX、δZX為線性誤差，m；εXX、εYX、εZX為角度誤差，rad。同理，利用其他軸(即Y、Z、A、C軸，其對應的絕對運動量分別為y、z、a、c)的幾何誤差亦可擬合得到相應的誤差模型(各模型的表達式可掃描本文首頁OSID二維碼獲得)。

2 工件分特征下的機床關鍵幾何誤差分析

2.1 復雜工件的形狀誤差建模

圖2所示為復雜工件的三維模型，該工件由尺寸分別200 mm×200 mm×10 mm、160 mm×160 mm×10 mm的兩個長方體，長寬均為120 mm、坡度為10°的楔體，底面半徑為40 mm、圓錐角為30°、傾斜10°的圓錐臺以及底面半徑為25 mm、高度為10 mm、傾斜10°的圓柱組成。

圖2 復雜工件的三維模型

復雜工件的形狀誤差建模是形狀誤差分析的前提和基礎。如圖3所示，首先，基于復雜工件的三維模型進行特征分解，得到平面、斜面、圓柱和圓錐臺四個典型特征。然后，基于已規劃好的刀具路徑，使用UG軟件的后處理功能分別獲取五軸數控機床加工不同特征時的NC代碼。隨后，將機床各軸的理想運動量代入式(2)所示的幾何誤差模型中，即求得刀具路徑中每個切削位置上各幾何誤差的值。最后，將復雜工件的幾何誤差值代入式(1)所示的體積誤差模型中，即可得到其形狀誤差模型。

圖3 復雜工件的特征分解

2.2 工件分特征下的靈敏度分析

本文提出了一種工件分特征下的五軸數控機床關鍵幾何誤差分析與補償方法，用以分析并辨識影響機床加工精度的關鍵幾何誤差，并對其進行針對性補償，進而提高機床的整體加工精度。靈敏度系數的確定是靈敏度分析的前提條件，它對靈敏度分析結果具有決定性的影響。一般來說，一個幾何誤差的靈敏度系數值越大，說明該幾何誤差對形狀誤差的影響就越大。由此可知，進行靈敏度分析之前需定義一個靈敏度系數，各幾何誤差在不同特征下的靈敏度系數可定義為[21]

(3)

式中，Sn為幾何誤差n(n=1,2,…，41)在不同特征下的靈敏度系數；[Da,Db]表示加工不同特征時刀具運動的軌跡長度D，其中D=Db-Da；En為僅考慮單一幾何誤差n得到的形狀誤差；dL(L=x,y,z,a,c)為對刀具路徑上形狀誤差的微分。

式(3)中，僅考慮單一幾何誤差n得到的工件形狀誤差En可由下式表示：

(4)

式中，EnX、EnY、EnZ分別為幾何誤差n在X、Y、Z方向上的誤差分量。

為了便于評估各幾何誤差對總幾何誤差的相對影響程度，對每個特征中所有幾何誤差的靈敏度系數進行歸一化處理，定義了歸一化靈敏度系數Un，其表達式為

(5)

各特征的41項幾何誤差的歸一化靈敏度系數之和為1。

2.2.1圓錐臺特征的靈敏度分析

本文以圓錐臺為例，詳細闡述了靈敏度分析過程。將工件的三維模型導入到UG中，并設置加工工藝及參數，使用UG的后處理功能獲取加工圓錐臺時的NC代碼，即可得到機床五個軸的理想運動量。圓錐臺刀具路徑及五個軸的理想運動量如圖4所示。

(a)刀具路徑 (b)A軸運動量 (c)C軸運動量

將加工圓錐臺時機床各軸的理想運動量代入對應的機床幾何誤差模型中，即可求出圓錐臺各位置的幾何誤差值。最后將圓錐臺的幾何誤差值代入到機床的體積誤差模型中，即可得到圓錐臺的形狀誤差。圖5a～圖5d分別表示由幾何誤差δYZ、δZZ、δXX、δXA引起的圓錐臺形狀誤差在X/Y/Z方向上的分量。同理，其他幾何誤差引起的圓錐臺形狀誤差亦可求得。

(a)誤差δYZ

由式(3)～式(5)即可求出幾何誤差δYZ、δZZ、δXX、δXA在圓錐臺特征中的歸一化靈敏度系數。同理，亦可求出其他幾何誤差在圓錐臺特征中的歸一化靈敏度系數。圓錐臺特征的靈敏度分析結果如圖6所示，可以看出，δYZ、δZZ、δXX、δXA這四項幾何誤差的歸一化靈敏度系數之和為0.6。其中，幾何誤差δYZ的歸一化靈敏度系數為0.262，遠大于其他幾何誤差對圓錐臺形狀誤差的影響，因此在后續的補償過程中，對幾何誤差δYZ的補償是需要重點考慮的。

圖6 圓錐臺特征的靈敏度分析結果

2.2.2圓柱特征的靈敏度分析

同理，按照上述靈敏度分析方法，可得到各幾何誤差在圓柱特征中的歸一化靈敏度系數，分析結果如圖7所示，可以看出，δYZ、δZZ、δXX這三項幾何誤差的歸一化靈敏度系數之和為0.54。其中幾何誤差δYZ的歸一化靈敏度系數為0.295，遠大于其他幾何誤差對圓柱形狀誤差的影響，因此在后續的補償過程中，對幾何誤差δYZ的補償是需要重點考慮的。

圖7 圓柱特征的靈敏度分析結果

對比圖6和圖7可得，圓柱和圓錐臺特征中，歸一化靈敏度系數大小排在前三的幾何誤差均相同，依次為δYZ、δZZ、δXX，但其他幾何誤差的影響卻是不同的，并且圓柱和圓錐臺特征中相同幾何誤差的歸一化靈敏度系數值亦不相同。由此可知，對于有典型特征的工件，分特征地進行靈敏度分析可有效地辨識幾何誤差之間的差異，為后續補償提供更加準確的數據支撐。

本文定義歸一化靈敏度系數大于0.03的幾何誤差為關鍵幾何誤差，從圖6和圖7中可得到影響圓柱和圓錐臺的關鍵幾何誤差，結果如表2所示。從表2中可知，對于圓柱特征，共有12項關鍵幾何誤差，其中線性誤差有11項；對于圓錐臺特征，共有11項關鍵幾何誤差，其中線性誤差有9項。由此可認為線性誤差是影響圓柱和圓錐臺形狀誤差的重要因素。

表2 影響圓柱和圓錐臺關鍵幾何誤差

2.2.3平面與斜面特征的靈敏度分析

由于機床的PIGEs為與位置無關的幾何誤差，PDGEs為與位置有關的幾何誤差，則在本實驗中，平面和斜面的加工只需平動軸X/Y/Z運動，而旋轉軸A/C不動，因此旋轉軸的PIGEs對平面和斜面的幾何誤差有影響，而PDGEs對其無影響。

根據2.2.1節中求取圓錐臺的幾何誤差靈敏度系數的方法，同理亦可求出各幾何誤差在平面和斜面特征中的歸一化靈敏度系數，結果分別如圖8a和圖8b所示。對比圖8a和圖8b可得，平面和斜面特征中，兩者的關鍵幾何誤差較為相似，其中δZZ、δYX、δXY、δXX這四個幾何誤差的歸一化靈敏度系數之和約占總和的50%。平面和斜面特征中相同幾何誤差的歸一化靈敏度系數大小是不同的，其中關鍵幾何誤差SZY、δYY、SYX、δZX、SZX的靈敏度系數的數值大小有所差異。

(a)平面特征

在上述分析的基礎上，可得到影響平面和斜面特征的關鍵幾何誤差，如表3所示。從表3中可得，對于平面特征，共有10項關鍵幾何誤差，其中線性誤差有6項；對于斜面特征，共有11項關鍵幾何誤差，其中線性誤差有6項。由此可認為線性誤差是影響平面形狀誤差和斜面形狀誤差的重要因素。

表3 影響平面和斜面特征的關鍵幾何誤差

3 工件分特征下的機床關鍵幾何誤差補償實驗

由上述分析可得，平面、斜面、圓柱和圓錐臺四個特征的關鍵幾何誤差歸一化靈敏度系數之和占比均大于90%，分別為91.9%、92.1%、90.4%和90.8%。將上述辨識得到的四個特征的關鍵幾何誤差分別代入到機床的體積誤差模型中，計算其在總誤差中的占比，結果如表4所示。

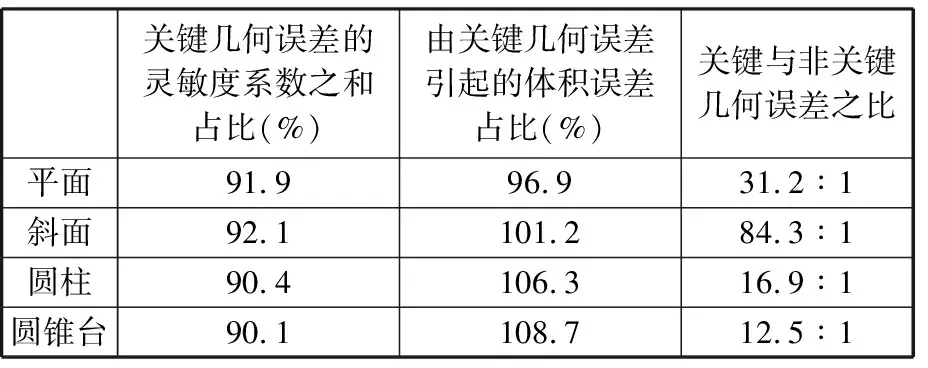
表4 關鍵幾何誤差占比分析

表4中，由關鍵幾何誤差引起的體積誤差占比在斜面、圓柱和圓錐臺特征中均大于1，表明由非關鍵幾何誤差引起的體積誤差占比分別為-1.2%、-6.3%、-8.7%，即說明關鍵幾何誤差與非關鍵幾何誤差對體積誤差中的作用效果相反。對比表4中結果可得，關鍵幾何誤差占比遠大于非關鍵幾何誤差占比，因此關鍵幾何誤差對體積誤差的影響起決定性作用，從而驗證了本方法的正確性。

本文在一臺型號為JDGR400 AC雙轉臺五軸數控機床上開展切削與補償實驗。將平面、斜面、圓柱和圓錐臺四個特征的關鍵幾何誤差分別代入式(1)所示的機床體積誤差模型中，參考文獻[22]中的方法，基于逆運動學計算補償后各軸的運動值，從而得到補償后的NC代碼。圖9所示為使用補償后的NC代碼進行切削加工的復雜工件。

圖9 補償后的復雜工件

按照圖10a所示的測點分布，在ZEISS三坐標測量機上對圖9所示的復雜工件補償前后的四個典型特征分別進行標定，如圖10b所示。補償前后的四個典型特征誤差平均值及補償率如表5所示。補償后四個特征的誤差平均值分別為8.8 μm、26.8 μm、4.9 μm和14.8 μm，其加工精度提高20%～30%，從而驗證了該方法的可行性與有效性。

(a)測點分布 (b)三坐標標定

表5 補償前后的四個典型特征誤差平均值及補償率

4 結論

(1)對于復雜工件的不同特征而言，影響工件形狀誤差的關鍵幾何誤差雖有相似之處，但同一幾何誤差的歸一化靈敏度系數在不同特征中的大小并不相同，因此在誤差補償中，對不同特征的工件應區別考慮。

(2)在分析得到的關鍵幾何誤差中，大多數幾何誤差為線性誤差，因此可認為線性誤差是影響平面、斜面、圓柱和圓錐臺這四個特征形狀誤差的重要因素。

(3)對于平面和斜面特征，其關鍵幾何誤差的歸一化靈敏度系數分布較均勻；對于圓柱和圓錐臺特征，影響較大的前三項關鍵幾何誤差δYZ、δZZ、δXX的歸一化靈敏度系數在總誤差中的占比較大，可達到50%以上。

(4)基于JDGR400 AC雙轉臺五軸數控機床的誤差補償實驗結果表明，補償后工件四個典型特征的加工精度提高了20%～30%。由此可知，本文提出的工件分特征下的靈敏度分析與補償方法能有效地提高機床的加工精度。