基于Midas Civil 的橋梁抗震安全性能驗算

韓雨

（中國市政工程中南設計研究總院有限公司，湖北 武漢 430014）

1 工程概況

本文以我國某橋梁工程為例展開分析，該項目設計橋寬為8m，跨徑為25m，采用預應力混凝土材料施工，各項技術指標如表1 所示。該橋梁的設計基準期為100年。地勘報告顯示建設地場地環境為Ⅱ類，沿線主要為旱地，地表坡度多為6°以下。該項目地處半干旱大陸性季風氣候帶，氣候表現為春季干燥且多風、夏季酷熱多雨、秋季溫暖涼爽、冬季寒冷漫長，不同季節的氣候較為分明。年平均風速約為4.1m/s，雨季主要集中在7、8 月份，雨季降水量約占到全年總降水量的65%～70%。到混凝土、鋼束的材料性質[1]，如表3 所示。

表1 項目主要技術指標

表2 端橫梁的基本尺寸參數

表3 主要材料性質表

根據設計方案建立簡支箱梁的基本模型，并采用SPC 在有限元軟件中分別導入梁端截面，并借助軟件自動計算各截面對應的形狀特性。各截面構造圖（以B-B面為例）如圖1 所示。

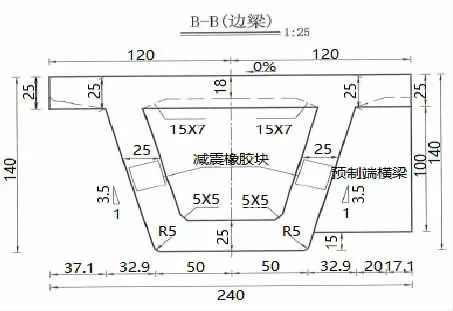
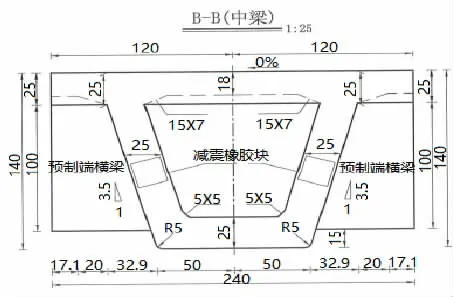
圖1 簡支箱梁的一般構造圖

箱梁之間采取剛接方式進行連接，且在箱梁的橫橋向上布置端橫梁，其基本尺寸參數如表2 所示。

2 有限元建模

定義材料及截面:

在Midas Civil 軟件內分別定義有限元建模所涉及

考慮到混凝土材料在施工、運營過程中可能發生的收縮、徐變等現象[2]，在定義材料時就需要對其特性隨時間變化做出假定，以C50 等級的混凝土為例，如表4 所示。

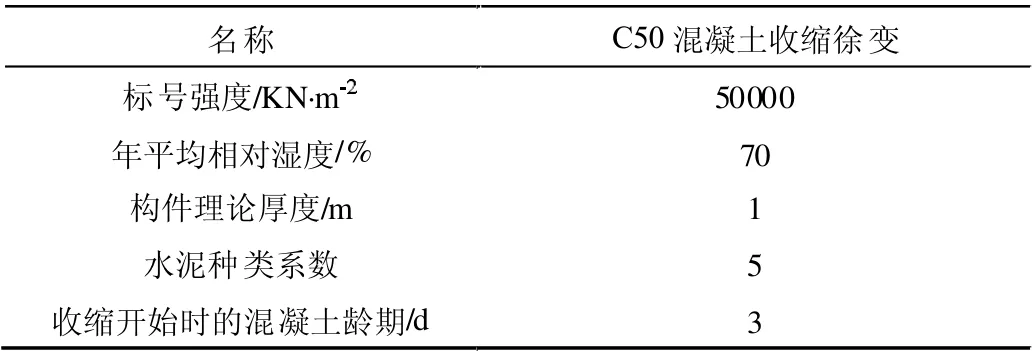
表4 C50 混凝土特性隨時間變化

3 輸入荷載

在該環節中對靜力荷載的工況條件做出定義，其中包括自重荷載、預應力荷載以及鋪裝施加的二期恒載[3]。

3.1 自重荷載

作為結構抗震計算的重要影響因素，自重荷載需要特別予以重視，在本項目中引入自重系數作為基本參數，分別定義X、Y、Z 向為0、0、-1，以此來轉化結構所受的自重荷載。

3.2 鋼束預應力荷載

在本項目中結構內共布置有96 條預應力鋼束，且均采取兩端張拉的方式施加預應力，預應力水平以1370000KN/m2為標準。

3.3 二期荷載

研究表明，鋪裝工序中所受的二期荷載對于結構剛度影響較為微弱，因此在結構分析時可忽略其對抗震性能的影響。但需要注意的是，應當充分重視其對結構體系質量矩陣的影響。基于施工所用的材料、工藝，計算相應鋪裝工程量后即可定義二期荷載。

3.4 輸入移動荷載數據

移動荷載的定義主要用于模擬橋梁上車輛荷載的作用，沿著車輛行進路線布置荷載來表示車輛行駛的全過程[4]。在這一荷載工況下求得結構內各位置所對應的最大及最小值，為結構設計、驗算提供數據支持。

按照表5 中的數據定義雙車道線，并完善各車道數據。對結構分別進行豎向基頻及特征值分析，得出結構響應的基頻為f=3.285047Hz。

表5 車道數據值

3.5 定義移動荷載工況

在定義移動荷載工況時需要將預先指定好的移動荷載按照一定條件施加到車道上完成分析，這一過程可遵照我國現行規范來確定各車道對應的折減系數。同時可借助Midas Civil 軟件基于車道數量自動定義橫向折減系數。隨后，即可定義子荷載工況條件，按照設計方案分別給出左、右車道的工況。

4 輸入反應譜數據

給定某一地震作用，可測得結構體系在該作用下的反應時程曲線，選擇反應的最大值，即可視為反應譜曲線上的一個元素點。按照我國現行《公路橋梁抗震細則》即可計算得出水平設計加速度反應譜S：

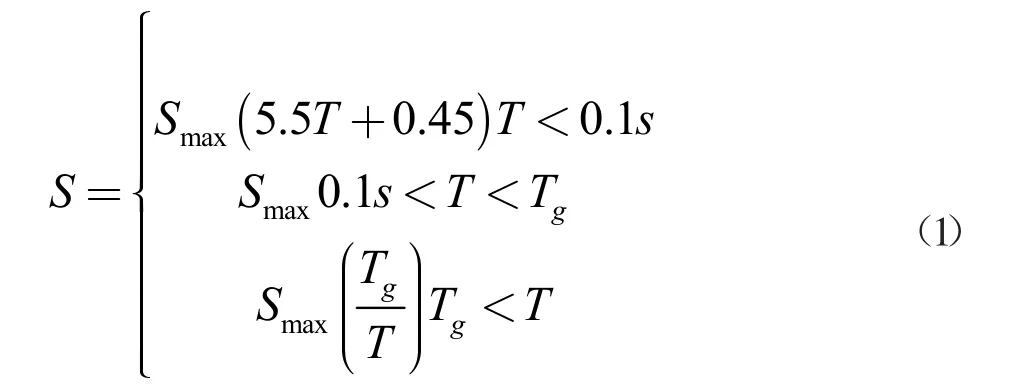
其中，Tg為特征周期，s；T 為自振周期，s；Smax為水平設計加速度反應譜最大值，按照下式求解：

Smax=2.25CiCsCdA

其中，Ci為抗震重要性系數；Cs為場地系數；Cd為阻尼調整系數；A 為水平向設計基本地震加速度峰值。

在本研究中進行抗震設計時，選用振型分解反應譜法進行計算，其在輸入荷載時所采用的基本參數如表6所示。

表6 地震荷載參數表

4.1 輸入反應譜函數

在有限元分析開始前，首先需要在模型中導入反應譜函數。對于小震作用，一般可采取振型分解反應譜法完成結構的可靠度分析。

4.2 定義特征值

在綜合采用振型分解反應譜法及振型疊加法開展結構可靠度分析時，Midas Civil 軟件給定了三種不同的分析方式：子空間迭代法、Lanczos 法以及多重Ritz 向量法。考慮到運算效率的影響，在本研究中選定多重Ritz 向量法進行分析，該方法能夠更為快速地使得參與質量系數大于90%。在Midas Civil 軟件中分別沿X、Y、Z 方向定義10 組加速度，并使其自由疊加，以此得到30 組不同的荷載工況。

4.3 定義反應譜荷載工況

一般而言，在路橋工程設計中僅需考慮水平向地震作用的影響，在本研究中也僅考慮X 向及Y 向的作用，因此在Midas Civil 軟件中分別定義順橋向、橫橋向的荷載工況。在組合振型時軟件提供了四種不同的方式：

4.3.1 完整二次項組合法(CQC 法)，該方法主要用于振型分布較為密集的結構體系。

4.3.3 ABS 法

ABS 法對不同振型作用下所產生的效應幅值進行疊加求和，考慮到結構各振型的最大值并非同時出現，所以該方法相對保守。

4.3.4 線性法

線性法對不同振型作用下所產生的效應進行疊加求和，同樣該法也具有保守的特點。

綜合考慮上述各方法的適用范圍及特點，最終選用CQC 法進行分析。

5 反應譜分析

5.1 振型及頻率

通過Midas Civil 軟件分析即可得出結構在地震作用下各模態的振型及頻率。借助利茲向量法即可求得結構在地震作用響應的前30 階振型如表8 所示，其中X、Y、Z 三個方向上振型的參與質量分別為99.35%、99.11%及96.75%，均達到了我國現行規范所要求的90%限值。根據振型分解結果可以發現：振型1、振型2、振型3 及振型4 分別為順橋向第一階振型、橫橋向第一階振型、豎向扭轉振型及橫向扭轉振型。

5.2 抗震驗算

由于簡支梁橋具有結構簡單、分布對稱的特點，因此在地震作用下結構往往能夠保有較好的完整性，即梁體破壞較少，破壞大部分為支座脫落、落梁等。下面主要以橋墩為對象進行抗震設計。

5.2.1 彈性驗算

遵照我國現行規范要求，驗算地震作用下橋墩結構的抗剪強度、位移是否滿足要求。反應譜的驗算主要可分為兩個不同的階段，其一為檢驗橋墩結構在地震作用下是否始終處于彈性狀態，因此首先應當按照彈性狀態做出驗算。

Midas Civil 軟件分析發現橋墩結構中有部分位置已經超過了彈性極限，進入塑性狀態，難以達到預期承載能力要求。因此，還應當對其塑性狀態進行驗算。修正參數，使其滿足彈塑性分析要求。

5.2.2 彈塑性驗算

在彈塑性狀態下的有限元分析中，可不對橋墩的強度進行驗算。這主要是因為此時橋墩已經超越彈性極限進入到塑性，需要控制的因素為結構變形量，因此只要結構的變形量滿足要求即可。在這一階段中主要以橋墩的抗剪強度、墩頂位移作為分析參數。

通過軟件分析，即可得到在地震作用下考慮彈塑性狀態橋墩的變形情況，如表7、表8 及表9 所示。

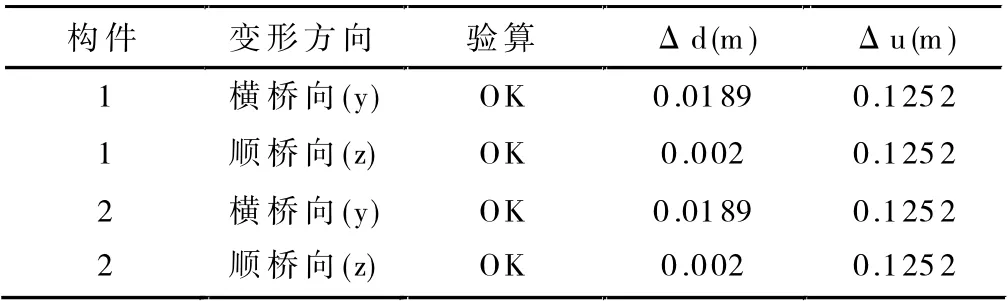
表7 1#墩頂位移驗算結果

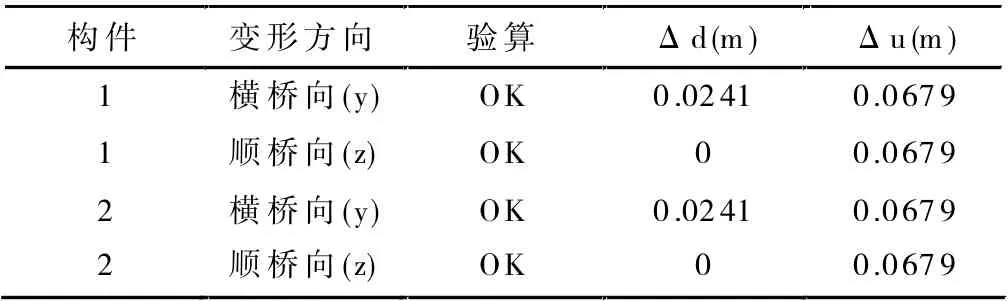
表8 2#墩頂位移驗算結果

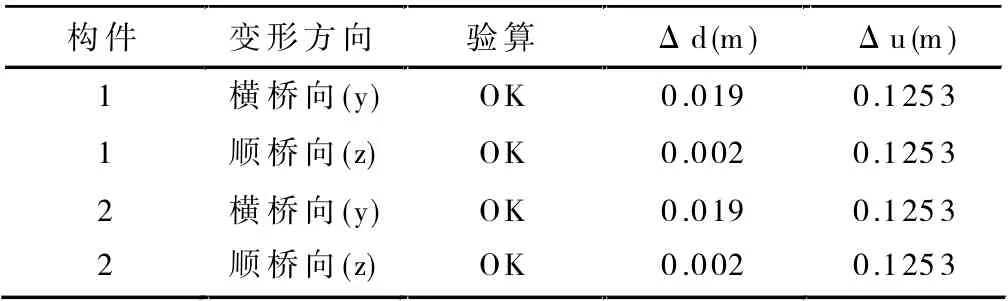
表9 3#墩頂位移驗算結果

其中，Δd 為地震作用下考慮彈塑性狀態墩頂的位移（m)；Δu 為地震作用下考慮彈塑性狀態墩柱的容許位移。根據上表中的數據可以發現，1#、2#、3# 橋墩在地震作用下的位移均能滿足預期要求。通過Midas Civil 軟件的后處理模塊查看塑性鉸區的抗剪強度，發現在地震作用下1#、2#、3# 橋墩的塑性鉸區抗剪強度均滿足預期要求。

6 結論

本文以我國某橋梁工程實例為基礎展開分析，借助Midas Civil 有限元分析軟件計算了在給定地震作用下結構的抗震性能。研究結果表明，在地震作用下橋墩結構部分位置達到塑性階段，在承受彎矩時首次屈服產生有限的局部變形，且伴隨承載能力的下降，未出現破壞現象，結構整體基本完整。各橋墩的變形量也處于允許范圍內，橋墩所受剪切強度小于容許值，滿足基本承載要求，不會出現倒塌、破壞的情況，滿足我國現行規范要求。