層狀各向異性介質海洋可控源電磁場靈敏度計算及特征分析
羅鳴, 裴建新, 葉益信
1 中國海洋大學海洋地球科學學院, 青島 266100 2 青島海洋科學與技術國家實驗室海洋礦產資源評價與探測技術功能實驗室, 青島 266100 3 東華理工大學地球物理與測控技術學院, 南昌 330013
0 引言
海洋可控源電磁法(Controlled-Source ElectroMagnetic method, CSEM)是一種有效探測海底油氣及礦產資源的海洋地球物理勘探方法(Constable,2010;柳建新等,2021).雖然海洋CSEM方法已被廣泛地應用于洋中脊和大陸邊緣地質構造研究以及海底油氣資源和天然氣水合物探測中,但該方法對各向異性地層的分辨能力依然不明確(Abubakar et al.,2010;Wirianto et al.,2010;周建美等,2017; Li et al.,2020).電磁場關于地下介質電阻率靈敏度的計算方法是求取電磁場分量對介質電阻率的導數,靈敏度分析是一種了解地電模型電磁場對探測目標分辨能力的有效方法,傳統的地球物理反演方法也需要精確計算電磁場關于地下介質電阻率的靈敏度.層狀介質的正反演是最基本且應用廣泛的數值模擬方法,同時能為二維和三維數值模擬提供參考.目前,電磁學家們已開發出了層狀介質海洋可控源電磁響應解析解的計算方法(Chave,1983;Everett and Constable,1999;Tompkins,2005;L?seth and Ursin,2007;Hunziker et al.,2015).由此,研究層狀介質靈敏度的解析計算方法是有必要且可行的.
海底地層常常呈現電阻率各向異性(Li et al., 2013;殷長春等,2014;羅鳴和李予國,2015;蔡紅柱等,2015;Yang and Qin,2020),垂直各向異性(VTI)是自然界中廣泛存在的各向異性情況,VTI反演是目前主要的電阻率各向異性反演解釋方法之一(Constable et al.,1987; Zhdanov et al., 2014;彭榮華等,2019).然而,在已有的地球物理文獻中,VTI反演存在高阻薄層橫向電阻率重構效果不佳的問題(Ramananjaona,2011;羅鳴等,2016;趙寧等,2017).對于該問題,鮮有文獻從靈敏度分析的角度討論可控源電磁對電阻率各向異性薄層的分辨能力(Constable and Weiss,2006;Christensen and Dodds,2007;Medina et al.,2010).Brown等(2012)通過分析層狀VTI模型電磁響應的有效異常討論了可控源電磁法對高阻薄層的分辨能力,然而,有效異常是關于各向同性模型電磁響應與各向異性模型電磁響應差異的參數,其本質為正演響應的特征分析,而非靈敏度分析.
目前,關于層狀介質的靈敏度解析計算的文獻并不多,Chave(1984)、Flosadóttir和Constable(1996)、Key(2009)推導了一維電阻率各向同性介質的靈敏度解析計算公式.Streich和Becken(2011)推導了垂直各向異性介質柱坐標系下x方向和z方向電偶極源的靈敏度計算公式并分析了陸地模型的靈敏度特征,但文獻中未推導y方向電偶極源的電磁場表達式和靈敏度解析公式.在模擬和解釋海洋CSEM資料時,地球物理數值模擬常在笛卡爾直角坐標系下進行,且通常假定發射源為理想的水平電偶極源.然而,在實際的海洋可控源電磁勘探作業中,由于洋流、波浪、潮汐等海水運動的影響,發射源可能會發生旋轉和傾斜等.復雜姿態的電偶極源可分解為三個相互正交方向的電偶極源,通過計算并矢量疊加三個方向發射源分量的電磁場,即可獲得復雜姿態下電偶極源產生的電磁場(羅鳴等,2017).因此,僅利用單一水平方向和垂直方向電偶源的電磁場和靈敏度計算公式并不能滿足復雜數值模擬的要求.
本文基于L?seth和Ursin(2007)提出的柱坐標系下電阻率垂直各向異性層狀介質單一水平方向電偶極源和垂直電偶極源電磁場的計算方法,推導了笛卡爾直角坐標系下三個正交方向電偶極源電磁場,并在此基礎上,詳細導出了電磁場分量關于各向異性電導率的靈敏度解析表達式.該方法適用于任意位置激發和任意位置接收的觀測系統.通過模擬電阻率各向異性海洋地電模型的電場靈敏度,分析不同方向電偶源電場對海底地層的橫向電阻率和垂向電阻率的靈敏度特征,比較不同方向電偶源對地層各向異性電阻率的分辨能力;基于模擬結果,進一步分析電場關于海底地層各向異性率的靈敏度特征,探討可行的電阻率各向異性反演策略.
1 層狀VTI介質海洋可控源電磁場表達式
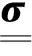
(1)
其中,σh為水平方向的電導率,σv為垂直方向的電導率.在VTI介質中,電磁場能夠分解為TE極化場和TM極化場,由此可得在第j層界面處的TE模式和TM模式反射系數r和透射系數t(圖1),其表達式如下:
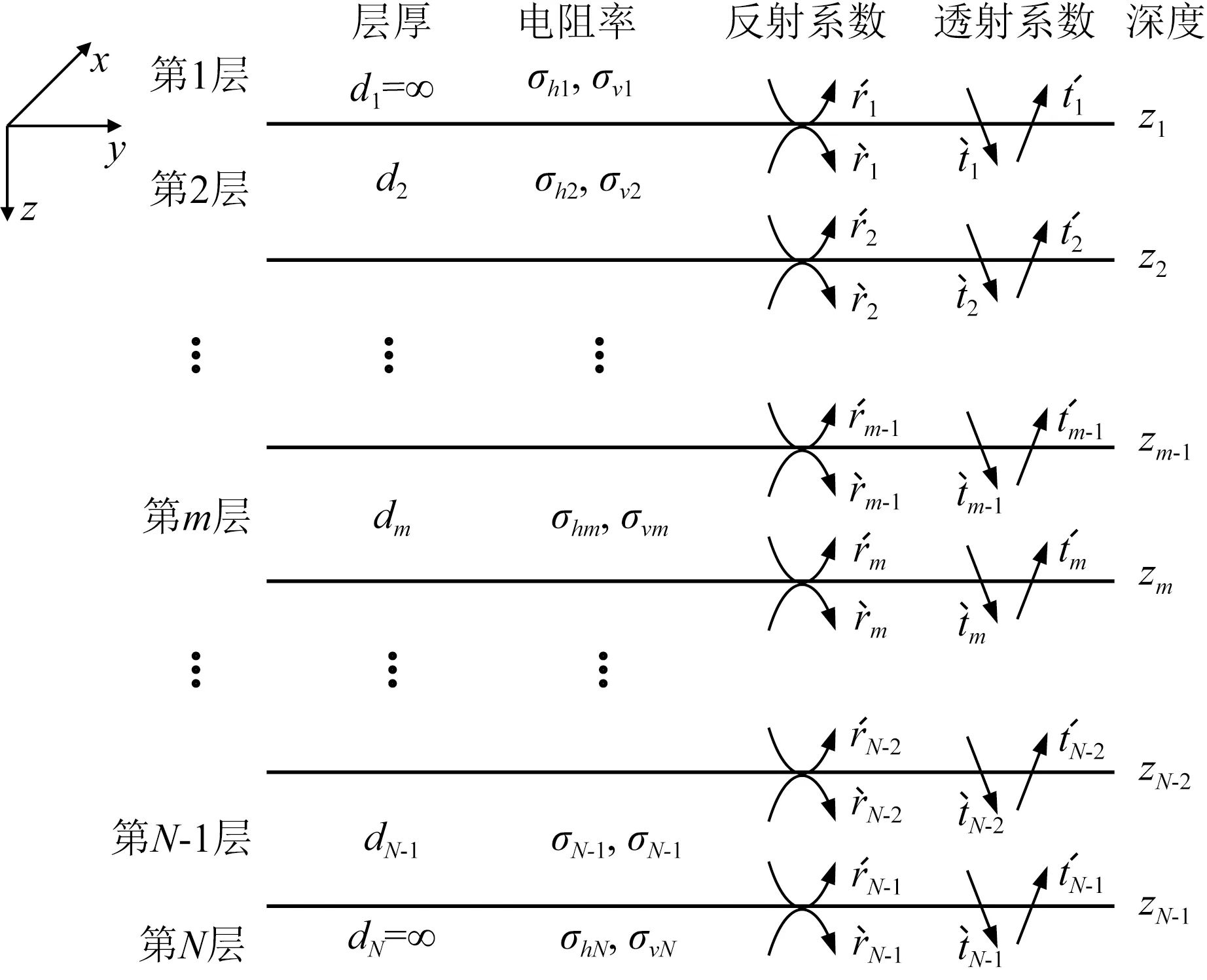
圖1 層狀VTI介質模型示意圖Fig.1 Schematic diagram of layered VTI medium model
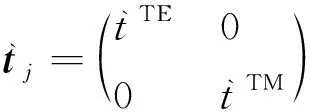
(2)
(3)
(4)
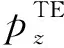
(5)
其中,μ0為真空中的磁導率,pρ=λ/ω,λ為Hankel變換濾波系數.
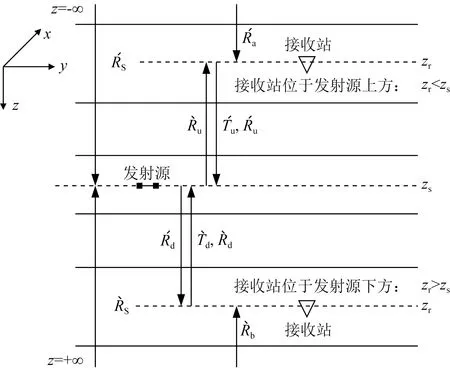
圖2 反射系數R和透射系數T遞推示意圖Fig.2 Diagram of recursion of reflection coefficient R and transmission coefficient T
(6)
(7)
復雜姿態的電偶極源可分解為三個相互正交方向的電偶極源,通過計算并矢量疊加三個方向發射源分量的電磁場,即可獲得復雜姿態下電偶極源產生的電磁場.假設發射源與接收點所在層具有電阻率各向同性或垂直各向異性(VTI),依據電磁波傳播理論遞推求得傳播矩陣,進一步可推導笛卡爾直角坐標系下x、y和z方向電偶極源任意位置激發,任意接收位置的電磁場表達式(L?seth and Ursin,2007;羅鳴和李予國,2015).
1.1 x方向水平電偶極源(xHED, Horizontal Electric Dipole)電磁場表達式
假設一個x方向發射源位于(xs,ys,zs),發射源長度為lx,發射電流為I安培,該發射源在層狀VTI介質接收站(x,y,z)處產生的電磁場為
(8)
(9)
(10)
(11)
(12)
(13)
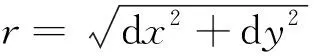
(14)
其中,當X=A,a1=1,a2=1;當X=D,a1=-1,a2=1.
②當接收站在源的下方時,即z≥zs(圖2),有
(15)

1.2 y方向水平電偶極源(yHED)電磁場表達式
假設一個y方向發射源位于(xs,ys,zs),發射源長度為ly,發射電流為I安培,該發射源在層狀VTI介質接收站(x,y,z)處產生的電磁場為
(16)
(17)
(18)
(19)
(20)
(21)
1.3 垂直電偶極源(VED, Vertical Electric Dipole)電磁場表達式
假設一個垂直方向發射源位于(xs,ys,zs),發射源長度為lz,發射電流為I安培,該發射源在層狀VTI介質接收站(x,y,z)處產生的電磁場為
(22)
(23)
(24)
(25)
×λ3J0(λr)dλ,
(26)
(2)針對實驗Ⅰ,有同學提出“Fe3+產生的原因可能是Cl-在陽極放電,生成的Cl2將Fe2+氧化”,寫出能支持這種假設的理由和相關反應的化學方程式:___。
在模擬VTI介質的空間域電磁場響應時,可通過數字濾波漢克爾變換實現由波數域到空間域的轉換(Anderson,1982).
2 偏導數的表達式
2.1 特征值的偏導數
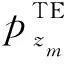
(27)
2.2 反射系數和透射系數的偏導數
①m層界面的反射、透射系數對σ{h,v}m的導數有
(28)
(29)
和
(30)
(31)
同理地,②m-1層界面的反射、透射系數對σ{h,v}m的導數有
(32)
(33)
和
(34)
(35)
2.3 遞歸反射響應和透射響應的偏導數

表1 方向向下遞歸響應的遞推范圍Table 1 Recursion parameters of downward recursive responses
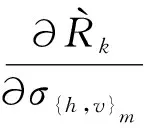
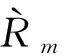
(36)

(37)
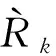
(38)
其中,Em=eiωpzmdm.
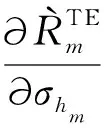
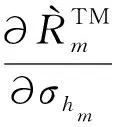
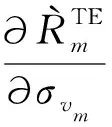
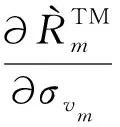
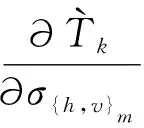
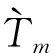
(39)
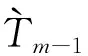
(40)
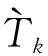
(41)

表2 方向向上遞歸響應的遞推范圍Table 2 Recursion parameters of upward recursive responses
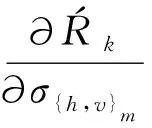
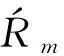
(42)
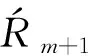
(43)
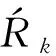
(44)
其中,Em=eiω pzmdm
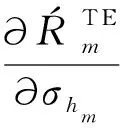
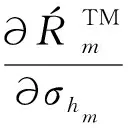
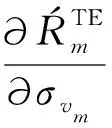
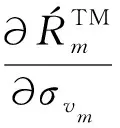
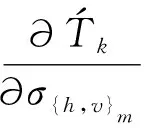
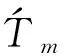
(45)
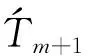
(46)
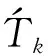
(47)
2.4 系數矩陣(RA,RD,RB,RC)的偏導數
系數矩陣R在不同發射源情況下取值不同:當發射源為HED時,電場和磁場分量的R分別取RA和RD;當發射源為VED時,電場和磁場分量的R分別取RB和RC.
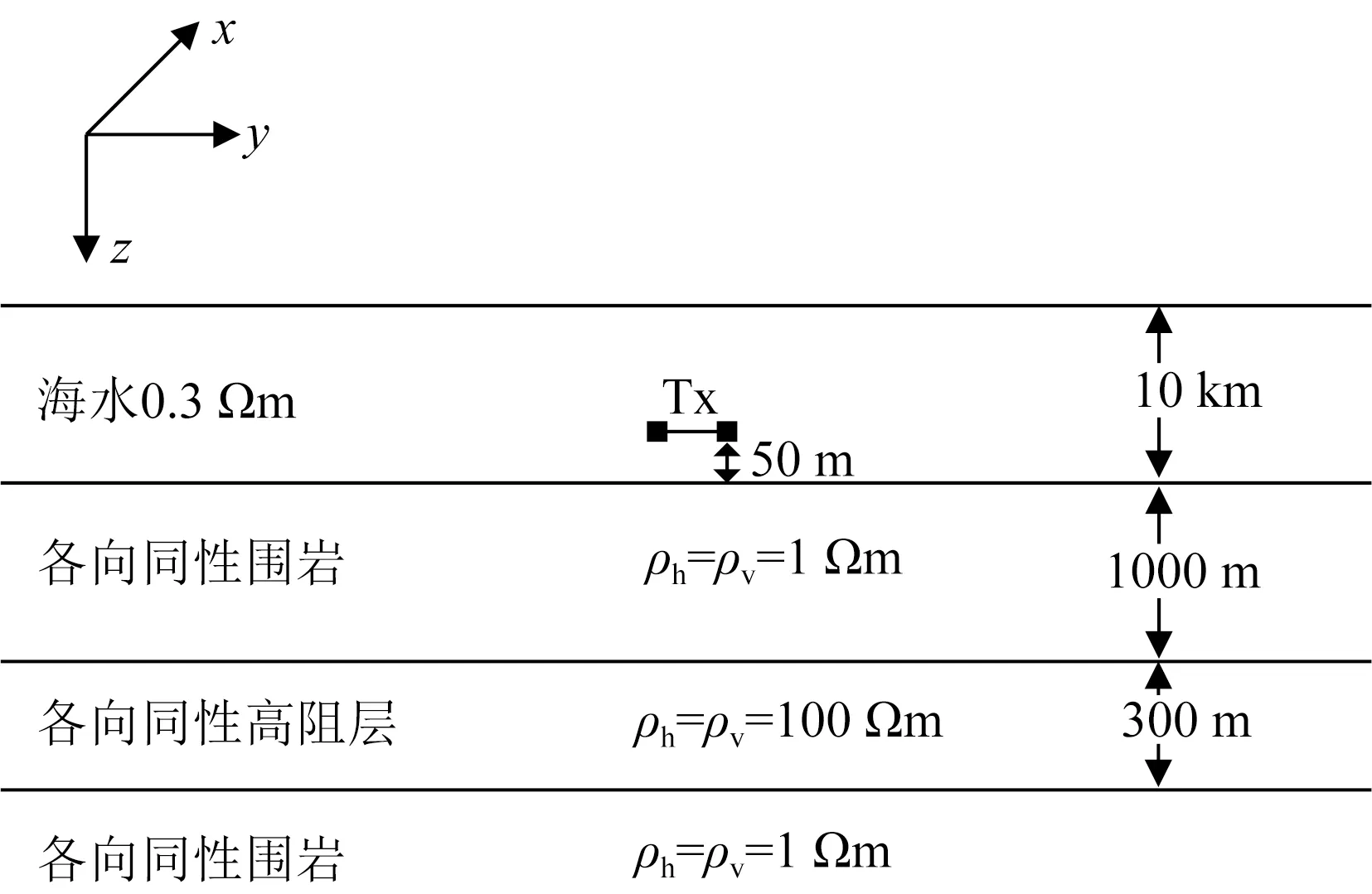
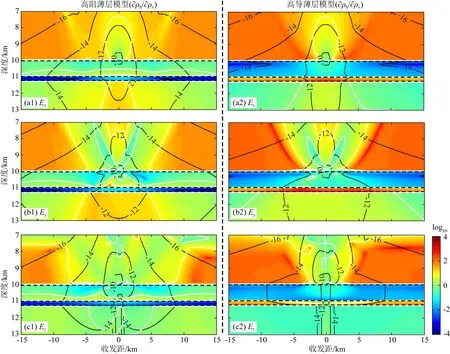
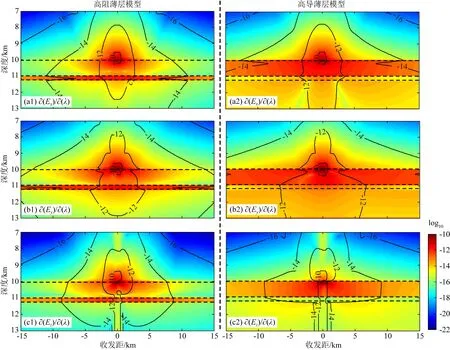
①當接收站在發射源的上方時,即z (48) 分別對系數矩陣(RA,RD,RB,RC)進行討論:當X=A,a1=1,a2=1;當X=D,a1=-1,a2=1;當X=B,a1=1,a2=-1;當X=C,a1=-1,a2=-1.其偏導數為 (49) 其中, ②當接收站在發射源的下方時,即z>zs, (50) 分別對系數矩陣(RA,RD,RB,RC)進行討論:當X=A,b1=1,b2=1;當X=D,b1=-1,b2=1;當X=B,b1=1,b2=-1;當X=C,b1=-1,b2=-1.其偏導數為 (51) 在計算偏導數時,如果遞推地層為包含多界面的復合層,反射和透射響應采用遞歸算式;如果是單一界面,則采用單一界面的反射和透射系數計算公式. x方向水平電偶極源: (52) (53) (54) (54) (56) (57) y方向水平電偶極源: (58) (59) (60) (61) (62) (63) 垂直電偶極: (64) (65) (66) (67) (68) 在海洋可控源電磁反演中,通常選擇電磁場關于地層電阻率對數的導數作為雅各比矩陣,因此,本文將靈敏度J定義為式(69)所示形式,并在后續的靈敏度驗算和分析中均使用該形式計算的靈敏度進行討論 (69) 其中,F為電磁場響應,ρh和ρv分別為橫向和垂向電阻率. 為驗證本文所提出偏導數算法的正確性,我們以圖3所示一維電阻率各向同性模型為例,將本文算法計算的結果與各向同性理論計算的結果進行對比.空氣波是海洋可控源電磁響應的主要干擾場之一,為了針對性地分析電磁場關于不同海底介質各向異性電阻率(ρh和ρv)的靈敏度,我們將海水層設為10 km以消除空氣波的影響.假設深度為10 km的海水層電阻率為0.3 Ωm,埋深為1 km、厚度為300 m高阻薄層的電阻率為100 Ωm,覆蓋層和基巖的電阻率均為1 Ωm.假設一個電偶極源布設于海底正上方50 m處,坐標為(0,0,9950),76個接收站等間距地布放于y方向測線0~15 km范圍的海底(測線位置x=0).發射頻率為0.25 Hz. 圖3 一維海洋電阻率各向同性地電模型Fig.3 1D canonical isotropic conductivity model (70) 圖4顯示了利用本文各向異性算法計算的三個正交方向電偶極源的電場靈敏度與各向同性算法計算結果的對比結果.圖中,藍線、紅線和綠線分別對應電場關于覆蓋層、高阻層和基巖的靈敏度曲線,‘+’線為各向同性算法計算的結果(Li and Li,2017).由圖可見,二者相對誤差均非常小,由此說明,本文提出的垂直各向異性介質靈敏度算法是正確的. 圖4 Ex(第一行)、Ey(第二行)和Ez(第三行)關于海底地層的橫向電阻率(第一列)、垂向電阻率(第二列)和各向同性電阻率(第三列)的靈敏度曲線;實線為本文算法的計算結果,‘+’線為各向同性算法的計算結果(Li and Li,2017),第四列為二者的相對誤差.Fig.4 Sensitivities of Ex (the 1st row), Ey (the 2nd row) and Ez (the 3rd row) to the horizontal resistivities (the 1st column), vertical resistivities (the 2nd column) and the sum of them (the 3rd column) for the sediment (blue curves), resistive reservoir (red curves) and basement (green curves) layers. The 3rd column shows the comparison between the sensitivities computed from this paper (solid lines) and the isotropic algorithm (‘+’ lines) (Li and Li, 2017) and the 4th column shows the relative error between them. 目前,海洋CSEM方法主要應用于探測數公里深度的油氣和礦產資源(Constable,2010),富含油氣的地層通常呈現出高于圍巖的電阻率值,該類模型可近似為高阻薄層鑲嵌于低阻圍巖的地電模型(簡稱為“高阻薄層模型”);而富含硫化物等礦體的地層通常呈現出低于圍巖的電阻率值(Peng et al., 2020),此類模型可近似為高導薄層鑲嵌于高阻圍巖的地電模型(簡稱為“高導薄層模型”).因此,我們分別建立高阻薄層模型和高導薄層模型,并設定空氣和海水層為電阻率各向同性,海底介質呈現電阻率各向異性.基于該兩個模型,分析不同方向電偶源和復雜姿態電偶源電場分量關于海底地層的橫向電阻率和垂向電阻率靈敏度特征.假設一個電偶源布設于海底正上方50 m處,151個接收站等間距地布放于y方向測線-15至15 km范圍的海底(測線位置x=0).發射頻率為0.25 Hz. 3.2.1 單一方向發射源的靈敏度 (1)y方向水平電偶源(yHED) 本小節分析yHED的靈敏度分布特征,此時發射源方向與測線方向相同,即為軸向觀測模式.為了更充分地對比和分析薄層對圍巖各向異性靈敏度的影響,我們首先分析海底介質為高阻各向異性半空間和高導各向異性半空間的靈敏度特征.假設高導各向異性半空間模型的下半空間橫向和垂向電阻率分別為ρh=1 Ωm和ρv=4 Ωm,高阻各向異性半空間模型的下半空間橫向和垂向電阻率分別為ρh=25 Ωm和ρv=100 Ωm.圖5為高導各向異性半空間模型(左)和高阻各向異性半空間模型(右)水平電場Ey關于橫向電阻率ρh靈敏度(a)、垂向電阻率ρv靈敏度(b),以及二者的比值(c)在yoz平面的分布圖.其中,黑線為電場log10|Ey|的等值線,圖5c中白線為水平電場Ey關于橫向電阻率ρh的靈敏度(用?ρh表示)與水平電場Ey關于垂向電阻率ρv的靈敏度(用?ρv表示)相等的等值線(即?ρh/?ρv=1).由圖5a和b可見,?ρh和?ρv均在發射源處最大,并隨著收發距和深度的增大而不斷衰減;高阻各向異性半空間模型的?ρh和?ρv具有與高導各向異性半空間模型相似的變化趨勢;在同一半空間模型中,?ρh在水平方向的衰減速度較于?ρv更快,然而在深度方向上?ρh比?ρv更慢.由圖5c可見,高阻各向異性半空間模型海底介質的?ρh/?ρv變化趨勢與高導半空間模型類似,表現為發射源下方?ρh/?ρv大于1,發射源兩側小于1,并隨著收發距增大而不斷衰減;在海底1 km的深度,高導各向異性半空間模型(圖5c1)海底介質的?ρh/?ρv在2 km收發距處出現極大值(約為7),在15 km收發距處出現極小值(約為0.01),而高阻各向異性半空間模型(圖5c2)海底介質的?ρh/?ρv在3 km收發距處出現極大值(約為10),在15 km收發距處出現極小值(約為0.1). 圖5 高導半空間模型(左)和高阻半空間模型(右)yHED水平電場Ey關于橫向電阻率ρh靈敏度(a)、垂向電阻率ρv靈敏度(b),以及二者的比值(c)在yoz平面的分布圖.需注意,(a)和(b)具有相同的色棒范圍Fig.5 The distribution of sensitivities of horizontal electric field Ey with respect to ρh (a) and ρv sensitivity (b) and their ratios (c) in yoz plane for the high conductivity half-space model (left) and the high resistivity half-space model (right). Note that (a) and (b) share the same color bar 為了說明海底分別存在高阻和高導薄層時電磁場關于地下介質的橫向電阻率和垂向電阻率的靈敏度特征,我們分別計算了高阻薄層模型和高導薄層模型的靈敏度.所選擇的高阻薄層模型在圖3所示模型基礎上,設定圍巖的橫向和垂向電阻率分別為ρh=1 Ωm和ρv=4 Ωm,薄層的橫向和垂向電阻率分別為ρh=25 Ωm和ρv=100 Ωm;而高導薄層模型則設定圍巖的橫向和垂向電阻率分別為ρh=25 Ωm和ρv=100 Ωm,薄層的橫向和垂向電阻率分別為ρh=1 Ωm和ρv=4 Ωm,其他參數不變.圖6為高阻薄層模型(左)和高導薄層模型(右)水平電場Ey關于橫向電阻率ρh靈敏度(a)、垂向電阻率ρv靈敏度(b),以及二者的比值(c)在yoz平面的分布圖.其中,黑線為電場log10|Ey|的等值線,圖6c中白線為?ρh/?ρv=1的等值線.對比圖5和圖6可見,當地下介質存在具有電性差異的薄層時,?ρh和?ρv分布都發生了改變:1)薄層模型和半空間模型的?ρh分布總體差異不大,主要是層狀模型覆蓋層靈敏度和薄層所在深度靈敏度的輕微改變;2)高阻薄層模型覆蓋層?ρv與半空間模型對應位置的?ρv(圖5a1)接近,而在薄層所在深度呈現出極大值,且薄層以下的圍巖?ρv略低于半空間模型(圖5b1)對應位置的?ρv;3)高導薄層模型覆蓋層?ρv顯著高于半空間模型(圖5a2)對應位置的?ρv,且在薄層所在深度呈現出極小值,薄層以下的圍巖?ρv略低于半空間模型(圖5b2)對應位置的?ρv;4)高阻薄層模型的?ρh/?ρv在薄層所在深度(海底以下1 km)出現了10-4量級的極小異常值,即高阻薄層的?ρh遠低于?ρv,而高導薄層模型的?ρh/?ρv在薄層所在深度(海底以下1 km)出現了103量級的極大異常值,即高阻薄層的?ρh遠高于?ρv. 圖6 高阻薄層模型(左)和高導薄層模型(右)yHED水平電場Ey關于ρh靈敏度(a)、ρv靈敏度(b),以及二者的比值(c)在yoz平面的分布圖.需注意,(a)和(b)具有相同的色棒范圍Fig.6 The distribution of sensitivities of Ey with respect to ρh (a) and ρv (b) and their ratios (c) in yoz plane for resistive thin layer model (left) and conductive thin model (right). Note that (a) and (b) share the same color bar 綜合以上算例結果可知,當海底僅存在一種介質時,無論是高導介質還是高阻介質,電場關于海底介質的橫向電阻率靈敏度?ρh和垂向電阻率靈敏度?ρv差異不大,且?ρh/?ρv沒有突變.當地下介質存在具有電性差異的薄層時,薄層將影響圍巖電阻率靈敏度分布,且在薄層所在深度出現?ρh/?ρv突變,具體表現為:高阻薄層對低阻圍巖的靈敏度分布影響較小,高阻薄層?ρh/?ρv呈現出低值異常;高導薄層對高阻覆蓋層?ρv影響劇烈,導致高阻覆蓋層?ρv明顯高于半空間?ρv,且高導薄層?ρh/?ρv呈現出高值異常. (2)x方向水平電偶源(xHED) 當發射源取向為x方向,此時發射源方向與測線方向垂直,即為赤道觀測模式.圖7為高阻薄層模型(左)和高導薄層模型(右)水平電場Ex關于橫向電阻率ρh靈敏度(a)、垂向電阻率ρv靈敏度(b),以及二者的比值(c)在yoz平面的分布圖.其中,黑線為電場log10|Ex|的等值線,圖7c中白線為?ρh/?ρv=1的等值線.對比圖6和圖7可見:1)赤道觀測模式的電場分量較于軸向觀測模式電場分量衰減更慢(對比電場等值線);2)赤道觀測模式的?ρh、?ρv和?ρh/?ρv的變化趨勢和幅值與軸向觀測模式都非常相近,即赤道觀測模式和軸向觀測模式對海底地層的各向異性電阻率分辨能力相近. 圖7 高阻薄層模型(左)和高導薄層模型(右)xHED水平電場Ex關于ρh靈敏度(a)、ρv靈敏度(b),以及二者的比值(c)在yoz平面的分布圖.需注意,(a)和(b)具有相同的色棒范圍Fig.7 The distribution of sensitivities of Ey with respect to ρh (a) and ρv (b) and their ratios (c) in yoz plane for resistive thin layer model (left) and conductive thin model (right). Note that (a) and (b) share the same color bar (3)垂直方向水平電偶源(VED) 圖8為高阻薄層模型(左)和高導薄層模型(右)垂直電場Ez關于橫向電阻率ρh靈敏度(a)、垂向電阻率ρv靈敏度(b),以及二者的比值(c)在yoz平面的分布圖.其中,黑線為電場log10|Ez|的等值線,圖8c中白線為?ρh/?ρv=1的等值線.對比圖6、圖7和圖8可見:1)垂直方向電偶源電場分量Ez在水平方向衰減速度均快于赤道觀測模式和軸向觀測模式電場分量(對比電場等值線);2)垂直方向電偶源的?ρh、?ρv和?ρh/?ρv的變化趨勢與軸向和赤道觀測模式相近,但靈敏度隨著收發距的增大而衰減更快.需注意的是,對于海底各向異性地層,垂直方向電偶源?ρh/?ρv較于軸向和赤道觀測模式更加接近于1,即垂直電偶源電場關于海底地層的橫向電阻率和垂向電阻率靈敏度的差異較于水平電偶源更小,由此說明,垂直電偶源對海底地層各向異性電阻率的分辨能力高于水平電偶源. 圖8 高阻薄層模型(左)和高導薄層模型(右)VED垂直電場Ez關于ρh靈敏度(a)、ρv靈敏度(b),以及二者的比值(c)在yoz平面的分布圖.需注意,(a)和(b)具有相同的色棒范圍Fig.8 The sensitivities distribution of Ey with respect to ρh (a) and ρv (b) and their ratios (c) in yoz plane for resistive thin layer model (left column) and conductive thin model (right column). Note that (a) and (b) share the same color bar 3.2.2 復雜姿態電偶極源的靈敏度 復雜姿態的電偶極源可通過計算并矢量疊加三個正交方向發射源分量的電磁場以獲得總電磁場,其對應的靈敏度也可通過三個正交方向的電偶源所激發電磁場的靈敏度疊加得到: J=JxHED+JyHED+JVED, 式中,J表示復雜姿態電偶極源的電磁場靈敏度,JVED表示垂直電偶極源(VED)的電磁場靈敏度,JxHED和JyHED分別表示沿x軸和y軸取向水平電偶極源的電磁場靈敏度. 假設一個y方向水平偶極源受到海流等綜合因素的影響,其姿態出現了旋轉和傾斜,假設其方位旋轉了30°(z軸不動,xoy平面順時針旋轉),并發生30°傾斜(x軸不動,yoz平面順時針旋轉).圖9為高阻薄層模型(左)和高導薄層模型(右)復雜姿態電偶極源Ex分量(a)、Ey分量(b)和Ez分量(c)關于ρh靈敏度與ρv靈敏度的比值在yoz平面的分布圖,其中黑線為電場等值線,白線為?ρh/?ρv=1的等值線.由圖9可見,由于電偶源姿態變化,Ey和Ez電場等值線和靈敏度均呈現非對稱分布;對比圖9a、b和c發現,Ex分量的?ρh/?ρv與Ey分量的?ρh/?ρv幅值非常接近,而Ez分量的?ρh/?ρv較于Ex和Ey分量都更加接近于1.從本算例結果發現,當電偶源發生姿態變化時,不同方向電場分量具備相應方向電偶源電場的特征;較于水平電場分量,垂直電場分量關于海底地層的橫向和垂向電阻率靈敏度差異最小,這種現象在薄層中更為明顯. 圖9 高阻薄層模型(左)和高導薄層模型(右)復雜姿態電偶極源Ex分量(a)、Ey分量(b)和Ez分量(c)關于ρh靈敏度與ρv靈敏度的比值在yoz平面的分布圖.需注意,a和b具有相同的色棒范圍Fig.9 The distribution of ratios of ? ρh and ? ρv for Ex (a), Ey (b) and Ez (c) in yoz plane for resistive thin layer model (left) and conductive thin model (right). Note that all subgraph share the same color bar 3.2.3 電磁場關于各向異性率λ的靈敏度 從以上算例發現,薄層的橫向電阻率靈敏度(?ρh)和垂向電阻率靈敏度(?ρv)差異明顯高于圍巖的?ρh和?ρv差異,且表現為高阻薄層?ρh遠小于?ρv,而高導薄層?ρh遠大于?ρv.?ρh和?ρv的巨大差異可能導致反演很難重構出靈敏度較低的電阻率值.假設反演能夠較為準確地重構海底地層的橫向電阻率ρh或垂向電阻率ρv,此時若能夠恢復較為準確的各向異性率λ,則可通過二者的關系λ重構出靈敏度較低的電阻率值.因此,我們進一步分析電場關于各向異性率λ的靈敏度特征. 電磁場關于各向異性率λ的靈敏度存在以下關系: (71) 采用上圖9所示算例相同的電偶源,即yHED方位旋轉30°,并傾斜30°.圖10為高阻薄層模型(左)和高導薄層模型(右)復雜姿態電偶極源Ex分量(a)、Ey分量(b)和Ez分量(c)關于各向異性率λ靈敏度在yoz平面的分布圖,其中黑線為電場等值線.對比圖10a、b和c發現,高阻薄層模型三分量電場關于各向異性率λ的靈敏度特征與ρv的靈敏度特征(圖6c1, 圖7c1, 圖8c1)非常接近,圍巖的?Ey/?λ略高于?Ex/?λ和?Ez/?λ,需注意的是,高阻薄層的三分量電場關于λ的靈敏度明顯高于ρh的靈敏度;高導薄層模型圍巖的三分量電場關于各向異性率λ的靈敏度特征與ρh的靈敏度特征(圖6c2, 圖7c2, 圖8c2)接近,但高導薄層的三分量電場關于λ的靈敏度明顯高于ρv的靈敏度.從本算例結果發現,電場分量關于λ的靈敏度綜合了橫向電阻率靈敏度?ρh和垂向電阻率靈敏度?ρv的特征;高阻薄層電場分量關于λ的靈敏度高于ρh的靈敏度,且高導薄層電場分量關于λ的靈敏度高于ρv的靈敏度,由此可知,反演中不直接重構低靈敏度的各向異性電阻率值,而通過反演各向異性率λ間接恢復低靈敏度的各向異性電阻率值將是一個可行的反演策略. 圖10 高阻薄層模型(左)和高導薄層模型(右)復雜姿態電偶極源Ex分量(a)、Ey分量(b)和Ez分量(c)關于各向異性率λ靈敏度在yoz平面的分布圖.需注意,a和b具有相同的色棒范圍Fig.10 The distribution of ratios of? ρh and ? ρv for Ex (a), Ey (b) and Ez (c) in yoz plane for resistive thin layer model (left column) and conductive thin model (right column). Note that all subgraph share the same color bar 本文推導了笛卡爾直角坐標系下,電阻率垂直各向異性介質中三個正交方向電偶極源電磁場關于各向異性電導率的靈敏度表達式.模擬了海底介質為高阻半空間模型和高導半空間模型,以及高導圍巖中存在高阻薄層模型和高阻圍巖中存在高導薄層模型的靈敏度.計算結果表明,當海底各向異性半空間存在具有電性差異的薄層時,薄層將顯著影響地下介質各向異性電阻率的靈敏度分布;高阻薄層所在深度橫向電阻率靈敏度和垂向電阻率靈敏度比值呈現低值異常;高導薄層引起高阻覆蓋層靈敏度明顯高于高阻半空間靈敏度,且高導薄層所在深度橫向電阻率靈敏度和垂向電阻率靈敏度比值呈現出高值異常;垂直電偶源對海底地層各向異性電阻率的分辨能力高于水平電偶源.對比各向異性率和各向異性電阻率靈敏度可見,電場分量關于各向異性率的靈敏度綜合了橫向電阻率靈敏度和垂向電阻率靈敏度的特征,通過反演各向異性率間接恢復低靈敏度的各向異性電阻率值是一個可行的反演策略. 致謝感謝匿名審稿人提出的寶貴意見.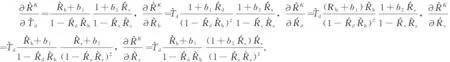
2.5 電磁場的偏導數
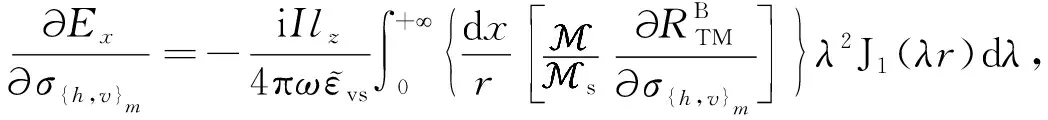

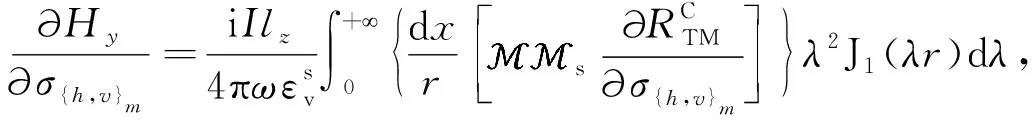
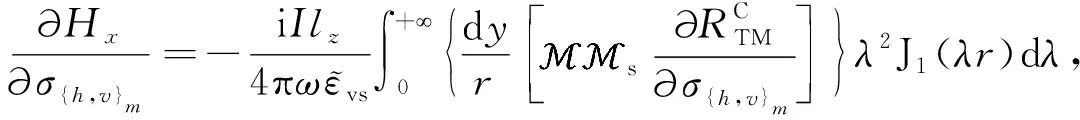
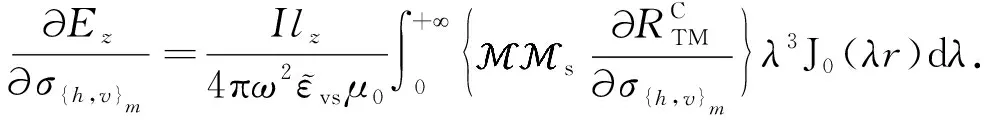

3 算例
3.1 靈敏度驗算
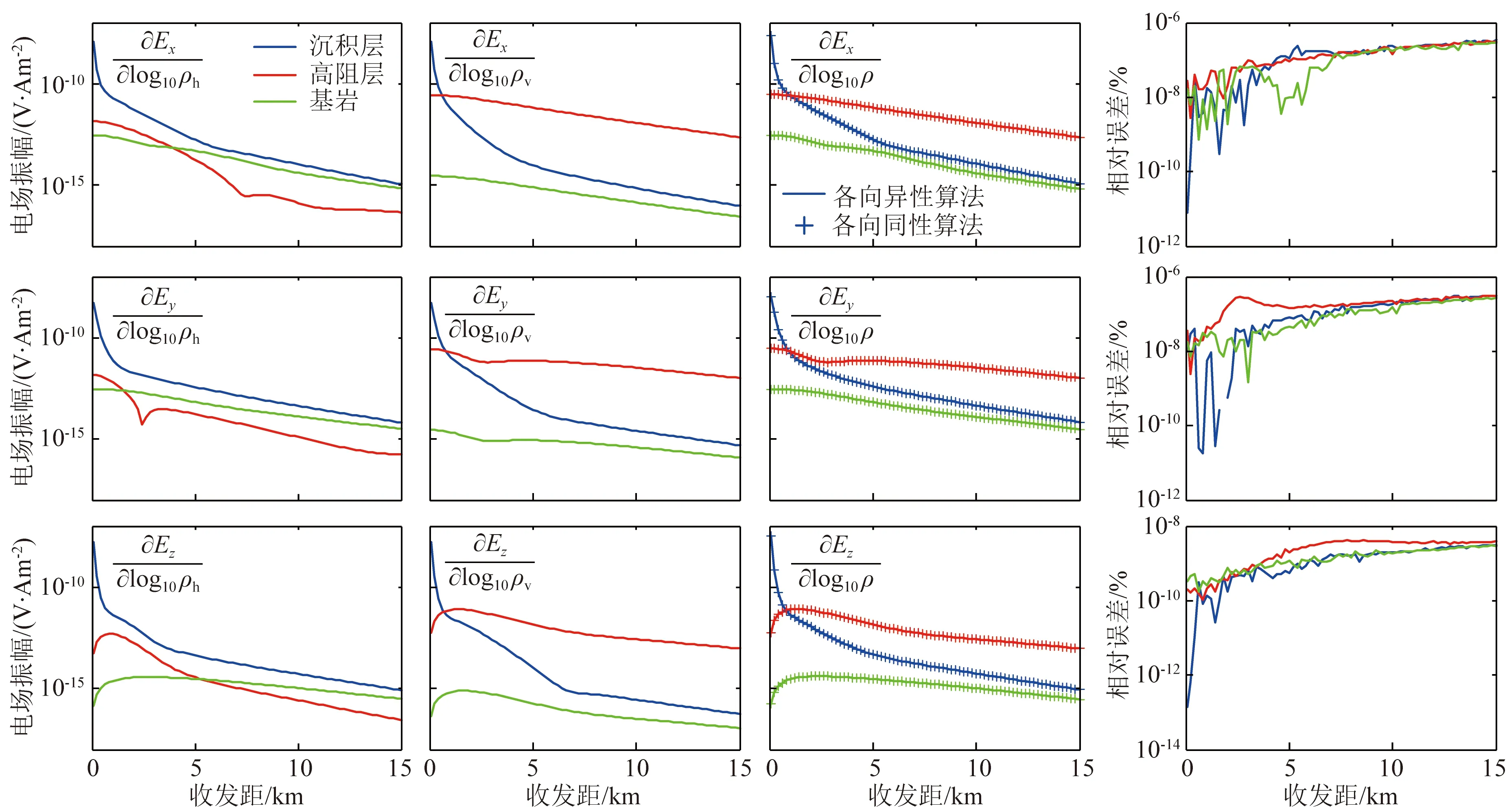
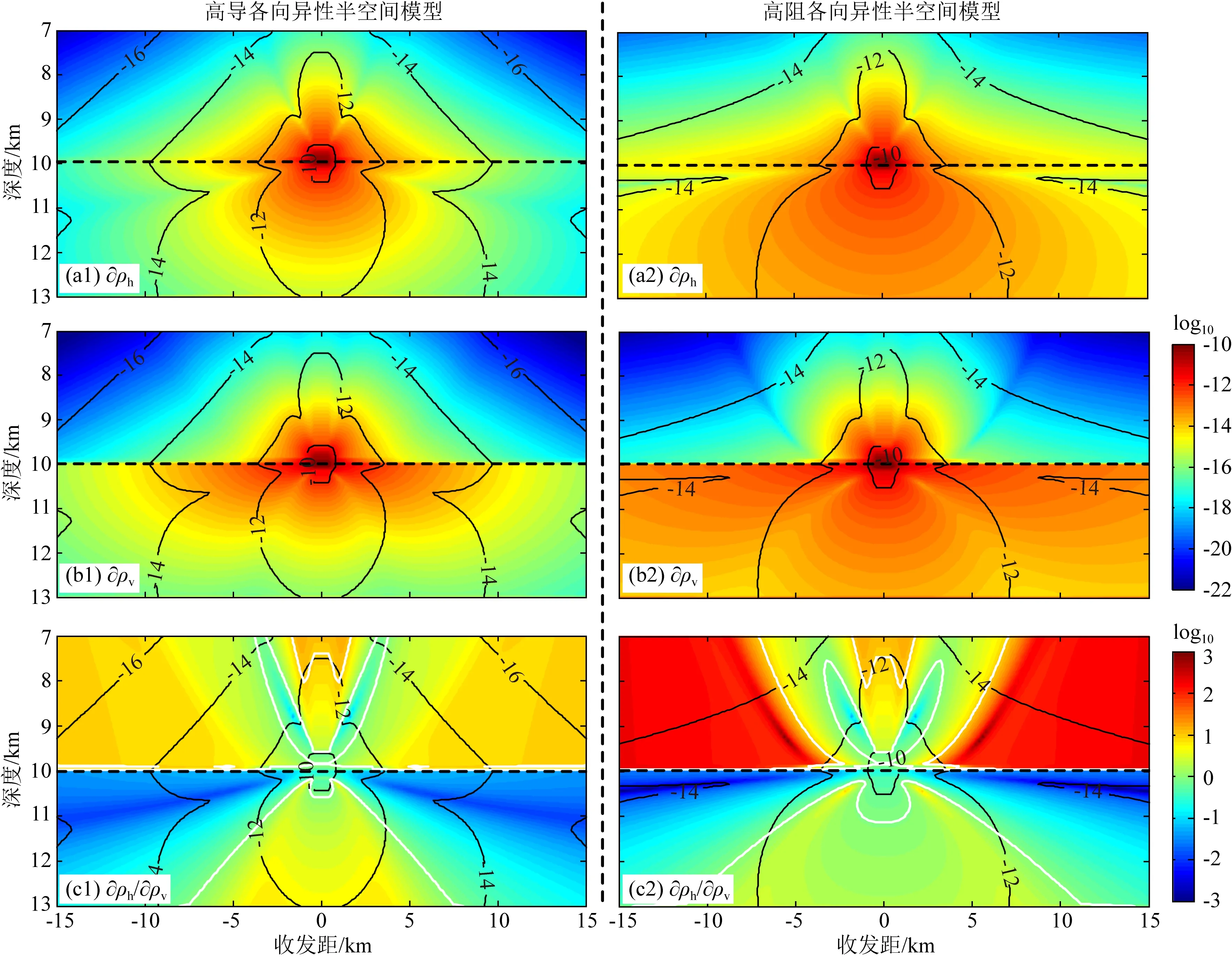
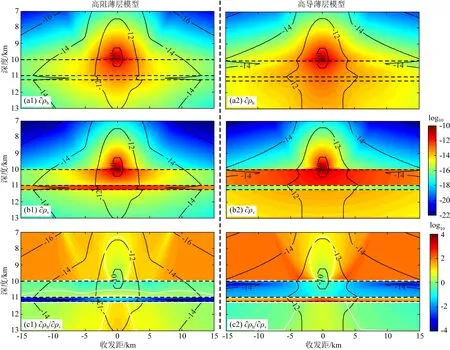
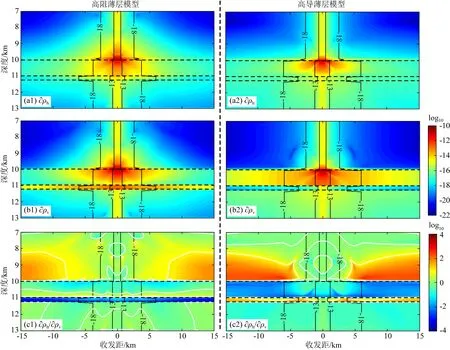
3.2 靈敏度分析

4 結論

