基于擴展方位彈性阻抗的裂縫參數及地應力參數預測方法

李林， 張廣智*

1 中國石油大學(華東)深層油氣重點實驗室， 青島 266580 2 中國石油大學(華東)地球科學與技術學院， 青島 266580

0 引言

隨著能源需求的增加和常規油氣資源的減少，非常規油氣資源(頁巖氣、致密氣和致密油儲層)成為石油行業的關鍵勘探目標.非常規儲層具有低孔低滲的特點，需要通過大規模的水力壓裂以提高油氣產量.地下裂縫能夠有效改善儲層的滲透率，地應力是控制水力壓裂的重要因素(陳志剛等，2020；王生奧等，2021)，因此利用高品質“五維”地震數據開展裂縫參數及地應力參數地震反演對于地下裂縫預測及水力壓裂具有重要意義(印興耀等，2018a，b).

早期的地應力預測模型假設地層為各向同性，將各向同性地應力預測模型應用于各向異性地層會導致地應力預測不準確，因此各向異性地應力模型更加符合非常規儲層的實際情況(趙小龍等，2020).許多學者考慮頁巖具有各向異性的微觀結構，提出了適用于垂直橫向各向同性(Vertical Transverse Isotropic, VTI)介質的地應力預測模型(Thiercelin and Plumb，1994；Higgins et al.，2008；鄧金根等，2013).張廣智等(2015)提出利用頁巖巖石物理等效模型進行地應力預測的方法.考慮到頁巖儲層中高角度裂縫較為發育的特征，Gray等(2012)推導了水平橫向各向同性(Horizontal Transverse Isotropic, HTI)介質中的水平應力預測方程，并指出將水平應力差異比(Differential Horizontal Stress Ratio，DHSR)作為衡量儲層是否能壓裂成網的指示因子.Far等(2016)研究了兩組正交的垂直裂縫嵌入VTI背景誘導的正交各向異性介質中的水平應力預測模型.馬妮等(2017，2018)推導了單組垂直裂縫嵌入VTI背景誘導的正交各向異性介質中的水平應力預測方程.

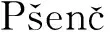
彈性阻抗(Elastic Impedance, EI)在預測彈性參數方面有著廣泛的應用前景(Connolly，1999；Whitcombe，2002；Wang et al.，2006；印興耀等，2013；Zong et al.，2013).Martins(2006)將彈性阻抗擴展到各向異性介質中，隨后許多學者研究了利用各向異性彈性阻抗提取各向異性參數的反演方法(陳懷震等，2014；Chen et al., 2018；Pan et al.，2020b；Li et al.，2020).Whitcombe等(2002)提出擴展彈性阻抗(Extended Elastic Impedance, EEI)的概念，通過擴展彈性阻抗可轉換為其他彈性參數、物性參數或地質力學參數，進而用于巖性、流體識別及地應力預測(Hafez and Castagna，2016；Aleardi，2018；Sharifi et al.，2019；Sharifi and Mirzakhanian，2019).研究表明深度、壓實趨勢、厚度和巖性等因素會影響EEI分析中的相關性趨勢(Ball et al.，2013；Thomas et al.，2013).Connolly(2019)指出彈性參數與擴展彈性阻抗的相關性取決于橫縱波速度平方比，且由于反演存在的誤差，最優的旋轉角應通過對反演結果而不是測井數據進行EEI分析得到.Russell和Hedlin(2019)基于Biot-Gassmann多孔彈性理論提出了擴展多孔彈性阻抗的概念，并指出擴展多孔彈性阻抗與彈性參數的相關性取決于干巖石的橫縱波速度平方比.

考慮單組垂直裂縫誘導的方位各向異性的影響，筆者將擴展彈性阻抗推廣到HTI介質中，提出擴展方位彈性阻抗的概念.首先推導HTI介質中的擴展方位彈性阻抗方程及其傅里葉級數展開表達式；基于推導的傅里葉系數(Fourier Coefficient，FC)方程，分析傅里葉系數與裂縫參數及DHSR之間的關系，進而提出一種基于擴展方位彈性阻抗的裂縫參數及DHSR預測方法，最后通過模型測試和實際應用驗證該方法在裂縫參數及DHSR預測方面的可靠性.

1 方法原理

1.1 HTI介質擴展方位彈性阻抗方程及傅里葉系數

HTI介質中的縱波反射系數方程為(潘新朋等，2018)：

+aδN(θ,φ)ΔδN+aδT(θ,φ)ΔδT，

(1)

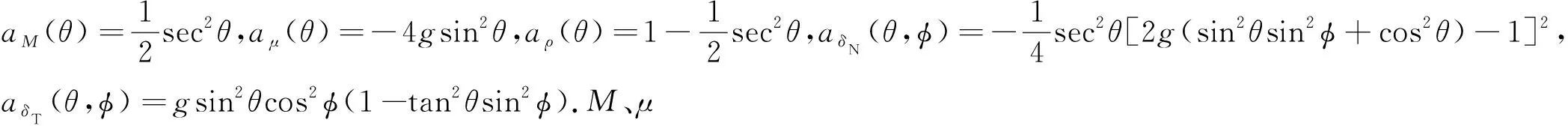
式(1)可重寫為：

RPP(θ,φ)=A+B(φ)sin2θ+C(φ)sin2θtan2θ，

(2)

式中：

(3)

(4)

(5)

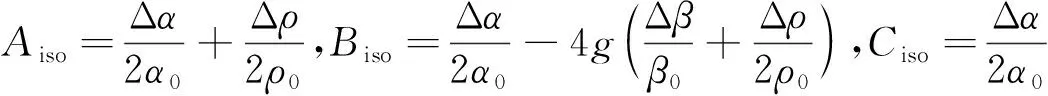
Whitcombe等(2002)推導了擴展彈性阻抗方程，通過改變單一的旋轉角即可由擴展彈性阻抗轉化為其他彈性參數.類比各向同性介質中的擴展彈性阻抗推導過程，將tan=sin2θ代入式(2)，左右兩邊同時乘以cos，得到：

Rcos=Acos+B(φ)sin

(6)

RPP(,φ)=Rcos(cos-sin)

=Ap()+B(φ)q()+C(φ)r()，

(7)

其中，p()=cos(cos-sin)，q()=sin(cos-sin)，r()=sin2.RPP(,φ)表示尺度化的方位反射系數.

彈性阻抗的定義為(Connolly, 1999)：

(8)

結合式(7)、(8)，通過推導可得到HTI介質中的擴展方位彈性阻抗方程為：

EEI(,

(9)

(10)

(11)

(12)

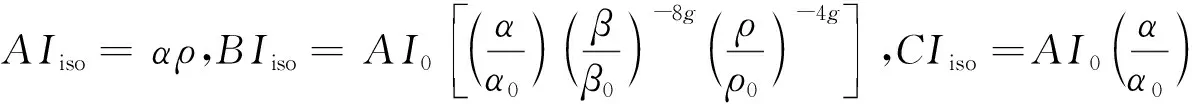
對式(9)兩邊同時取對數，得到歸一化的擴展方位彈性阻抗方程：

LEEI(,φ)=p()LAI+q()LBI(φ)+r()LCI(φ)，

(13)

其中，LEEI(,

對式(13)進行傅里葉級數展開，得到：

LE E I(,φ)=R0()+R2()cos(2φ)+R4()cos(4φ)，

(14)

R0()

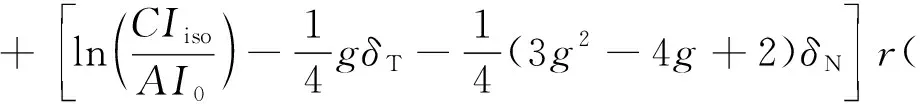
(15)

R2()=Baniq()+[g(g-1)δN]r()，

(16)

R4()，

(17)

式中，Rn(),(n=0,2,4)表示與旋轉角相關的傅里葉系數，Bani=g(δT-kδN)表示各向異性梯度.

傅里葉系數可通過式(18)計算：

Rn(,φi)cos(nφ)dφ/cos(nφsym)

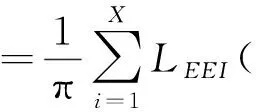
(18)

1.2 傅里葉系數與裂縫參數及DHSR的關系

Gray等(2012)推導了楊氏模量、泊松比及法向柔度表征的DHSR表達式，通過推導可得到由縱、橫波阻抗(IP和IS)及法向弱度表征的DHSR，其表達式為：

(19)

式(19)表明，DHSR僅與地層系數g和法向弱度δN有關.根據式(15)、(16)、(17)可知，零階傅里葉系數與各向同性參數及裂縫參數均有關，二階和四階傅里葉系數主要與裂縫參數有關.通過變化角，四階傅里葉系數只能轉化為而不能轉化為裂縫參數和DHSR，因此下面以某工區A井數據為例，分析零階和二階傅里葉系數與各向同性參數、裂縫參數及DHSR之間的關系.

圖1為A井中的各向同性參數及裂縫參數，包括縱、橫波速度、密度、法向及切向裂縫弱度.結合式(15)，利用井數據合成不同角情況下的零階傅里葉系數如圖2a所示，可以看出零階傅里葉系數隨著角的變化而變化.由于零階傅里葉系數與各向同性參數和裂縫參數均相關，因此分別計算零階傅里葉系數與各向同性參數、裂縫參數及DHSR的相關系數，如圖2b所示，可以看出縱、橫波速度、密度、法向弱度、切向弱度及DHSR與零階傅里葉系數的相關系數隨著角的變化而變化，縱、橫波速度、密度、法向弱度、切向弱度及DHSR與零階傅里葉系數的最大相關系數絕對值分別為0.96、0.99、0.83、0.72、0.74和0.74.可以看出法向弱度、切向弱度及DHSR與零階傅里葉系數的相關系數遠低于各向同性參數與零階傅里葉系數的相關系數.李林等(2020)研究表明，裂縫參數對零階傅里葉系數的貢獻遠小于各向同性參數的貢獻，導致零階傅里葉系數對裂縫參數的敏感性較低，因此零階傅里葉系數僅可用于估測各向同性參數，而不能用于裂縫參數和DHSR估測.

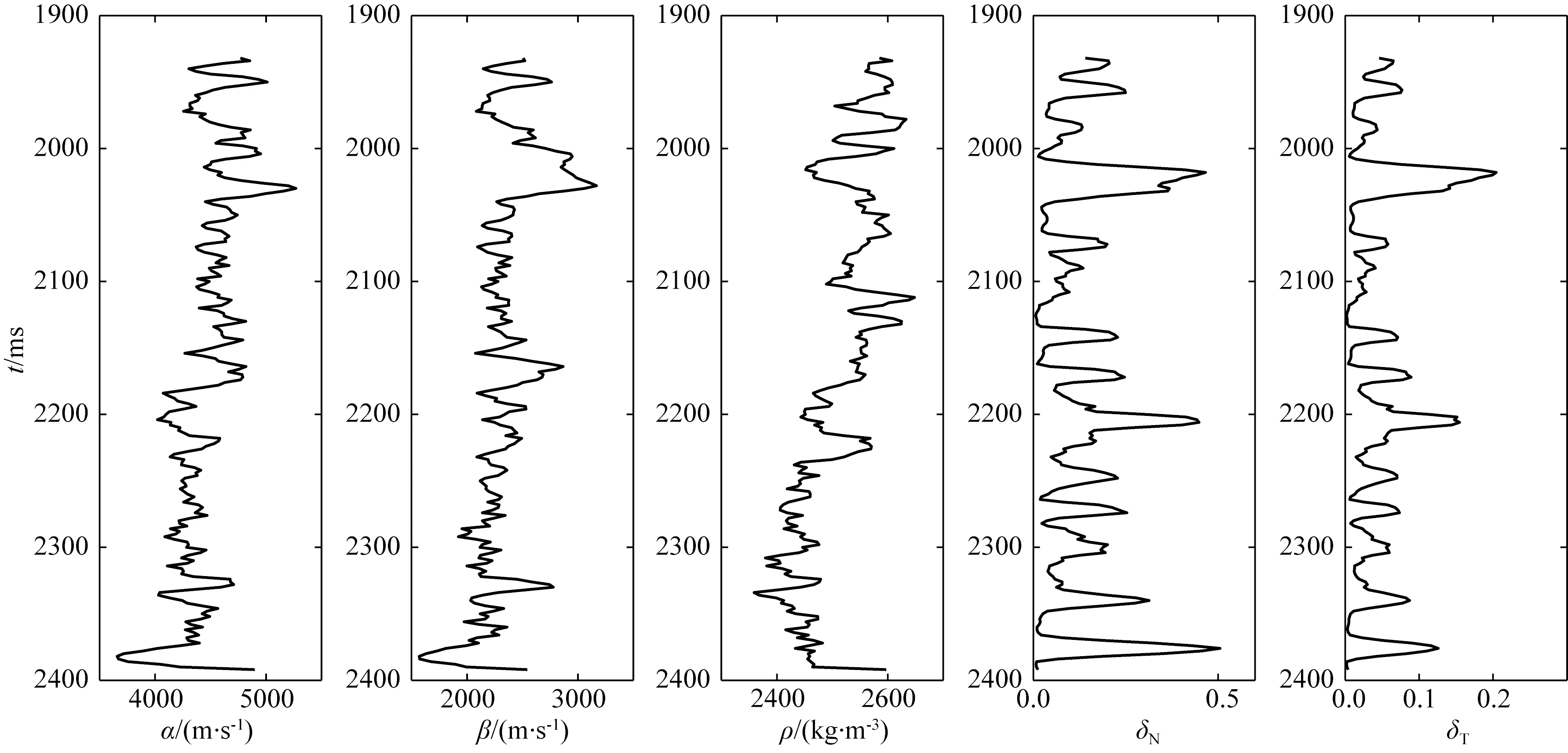
圖1 A井的各向同性參數及裂縫參數Fig.1 Isotropic parameters and fracture parameters of well A

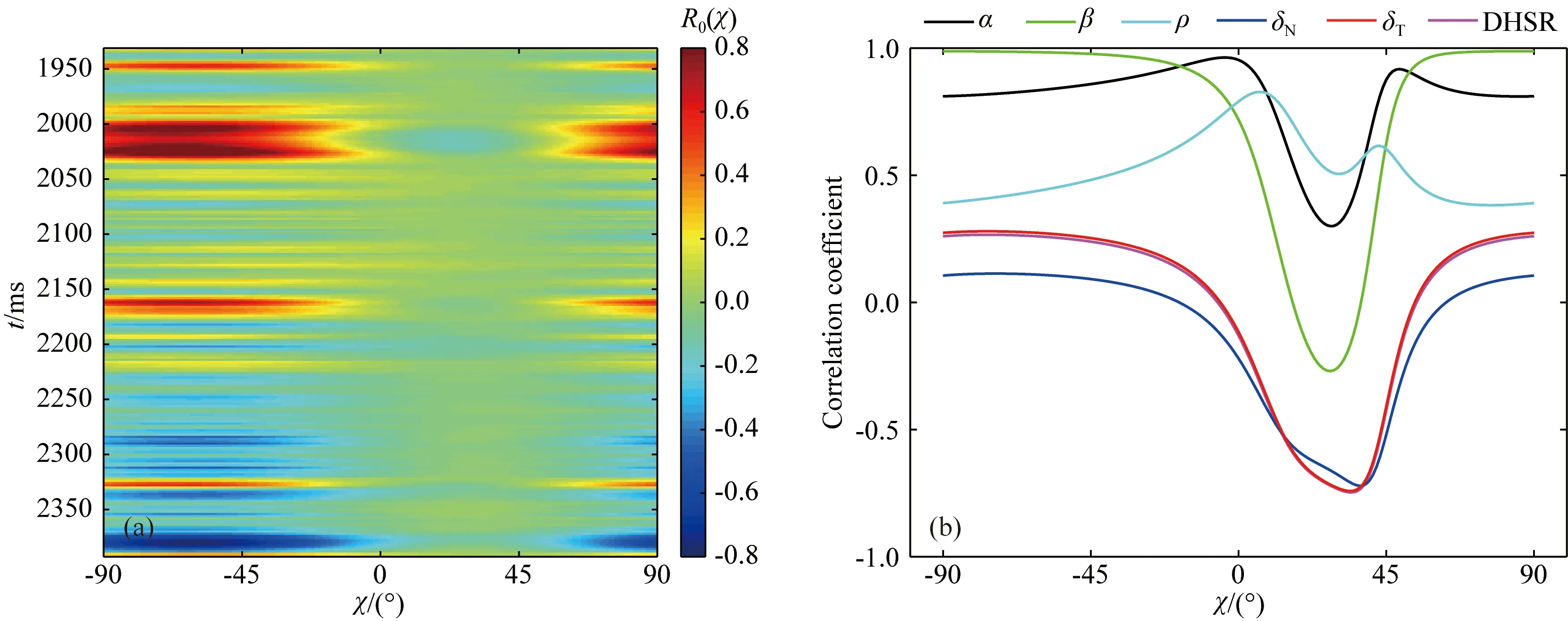
圖2 合成的(a)零階傅里葉系數，(b)零階傅里葉系數與各向同性參數、裂縫參數及DHSR的相關系數Fig.2 Synthetic (a) zeroth FC, and (b) correlation coefficients of the zeroth FC with isotropic parameters, fracture parameters and DHSR

圖3 合成的(a)二階傅里葉系數，(b)二階傅里葉系數與裂縫參數和DHSR的相關系數Fig.3 Synthetic (a) second FC, and (b) correlation coefficients of the second FC with fracture parameters and DHSR

R2(

(20)

R2(=90°)=-Bani+g(g-1)δN.

(21)

結合式(20)、(21)可得到各向異性梯度表達式：

Bani=2R2(=45°)-R2(=90°).

(22)

在疊前地震反演中，通常假設一段時窗內的地層系數g為一常數，例如假設g=0.25(Whitcombe et al.，2002；Russell and Hedlin，2019).結合各向異性梯度與裂縫參數的關系表達式，通過推導可得到：

(23)

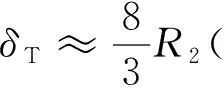
(24)

結合式(19)、(23)可得到HTI介質中的DHSR簡化表達式：

(25)

因此，當假設地層系數g為0.25時，利用式(23)、(24)、(25)即可由二階傅里葉系數分別估測HTI介質中的裂縫參數及DHSR.Connolly(2019)指出彈性參數與擴展彈性阻抗的相關性取決于地層系數g.本文研究表明，二階傅里葉系數與裂縫參數及DHSR的相關性也與地層系數g相關.由于地層系數g是隨著時間或深度變化的，因此在實際應用中應通過尋找二階傅里葉系數與裂縫參數及DHSR的最大相關系數，分別確定最優的角進行裂縫參數及DHSR預測.

1.3 分方位疊前地震貝葉斯反演

由于計算傅里葉系數要先反演得到截距阻抗、梯度阻抗及曲率阻抗，因此提出利用疊前地震三參數貝葉斯反演方法，通過分方位地震數據分別進行截距阻抗、梯度阻抗及曲率阻抗的同時反演.對于一個方位，m個入射角和n個時間采樣點情況下，式(2)可重寫為矩陣表達式：

(26)

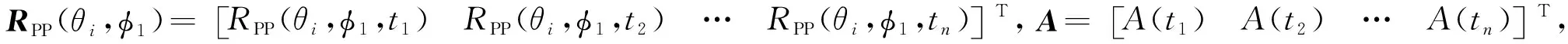
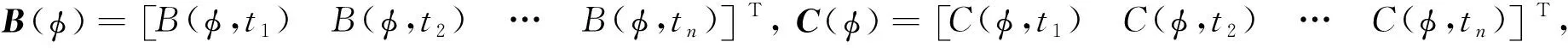
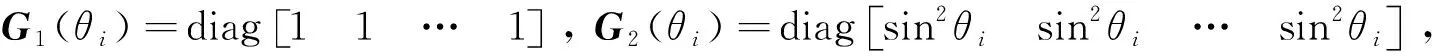
其中，上標T表示矩陣的轉置，符號diag表示對角矩陣.

考慮地震子波的影響，式(26)變為：

(27)

式中，W(θi)表示角度子波矩陣.

式(27)可進一步簡化為矩陣表達式：

d=Gm，

(28)

其中：

假設地震噪聲服從高斯分布，待反演模型參數的先驗信息服從柯西分布，則后驗概率密度函數可表示為：

(29)

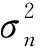
通過推導式(29)得到初始目標函數為：

(30)

其中，λQ表示柯西權重因子.由于地震數據缺乏低頻信息，引入低頻模型約束項能夠補充待反演參數的低頻信息，并提高反演的穩定性及橫向連續性(印興耀等，2013；Zong et al.，2013；潘新朋等，2018)，因此最終的目標函數為：

(31)

式中，λA、λB和λC分別為截距項、梯度項及曲率項的低頻權重因子，AI0、BI0(φ)和CI0(φ)分別為與截距阻抗、梯度阻抗及曲率阻抗相關的低頻模型，P為積分矩陣.

在求得A、B(φ)和C(φ)之后，利用道積分即可求得截距阻抗、梯度阻抗及曲率阻抗.通過調試不同的角合成擴展方位彈性阻抗，對其進行傅里葉級數展開得到傅里葉系數，計算二階傅里葉系數與井中裂縫參數及DHSR的最大相關系數，分別確定最優的角，進而實現裂縫參數及DHSR預測.

2 模型試算

利用某工區井數據開展模型測試，以驗證提出方法的有效性.將圖1中的井曲線和主頻為35 Hz的雷克子波褶積合成方位角道集，入射角范圍為5°～40°，以5°間隔，方位角分別為0°、45°、90°和135°.向合成的方位角道集中分別添加信噪比(Signal to noise ratio，S/N)為5和2的高斯噪聲以模擬觀測地震記錄.圖4展示了不同信噪比的合成方位角道集.圖5展示了不同信噪比情況下反演的歸一化的截距阻抗、梯度阻抗及曲率阻抗，圖6展示了不同信噪比情況下反演的歸一化的截距阻抗、梯度阻抗及曲率阻抗與真實值的相對誤差.可以看出截距阻抗反演結果的相對誤差最小，梯度阻抗和曲率阻抗反演結果的相對誤差相對較大.截距阻抗反演結果的總體相對誤差小于5%，而梯度阻抗和曲率阻抗反演結果的總體相對誤差小于10%，在局部區域有時接近20%，但總體而言，在信噪比為5和2時均能得到較好的截距阻抗、梯度阻抗及曲率阻抗反演結果.圖7展示了不同信噪比情況下反演的法向弱度、切向弱度及DHSR.圖8展示了不同信噪比情況下反演的法向弱度、切向弱度及DHSR與真實值的相對誤差.可以看出，隨著信噪比降低，法向弱度、切向弱度及DHSR反演結果的相對誤差均有所增加，但總體相對誤差均小于10%.分別計算不同信噪比情況下的反演結果與真實值的相關系數，信噪比為5情況下，反演的法向弱度、切向弱度及DHSR與真實值的相關系數分別為0.90、0.93和0.91；信噪比為2情況下，反演的法向弱度、切向弱度及DHSR與真實值的相關系數分別為0.83、0.84和0.84.因此，即使在信噪比為2情況下，利用提出的方法也能夠得到合理可靠的法向弱度、切向弱度及DHSR預測結果，驗證了該方法在預測裂縫參數及DHSR方面的有效性.

圖4 合成方位角道集(a) 信噪比為5； (b) 信噪比為2.Fig.4 Synthetic azimuthal angle gather(a) S/N=5； (b) S/N=2.

圖5 不同信噪比情況下的模型參數反演結果(a) 歸一化的截距阻抗； (b) 歸一化的梯度阻抗； (c) 歸一化的曲率阻抗.Fig.5 Inversion result of model parameters for different noise levels(a) Normalized intercept impedance； (b) Normalized gradient impedance； (c) Normalized curvature impedance.

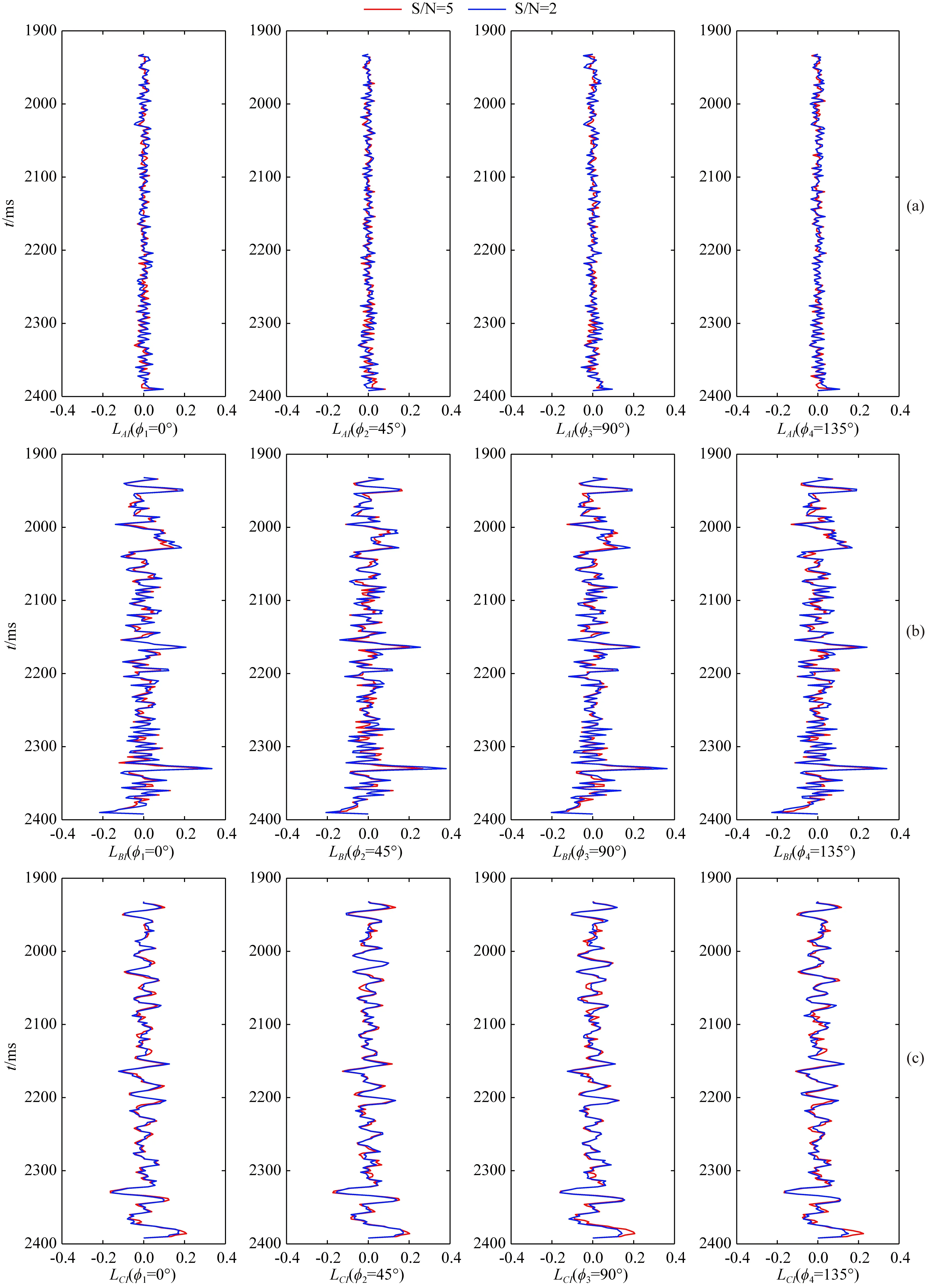
圖6 不同信噪比情況下模型參數反演結果與真實值的相對誤差(a) 歸一化的截距阻抗； (b) 歸一化的梯度阻抗； (c) 歸一化的曲率阻抗.Fig.6 Relative error between inversion result of model parameters and the true value for different noise levels(a) Normalized intercept impedance； (b) Normalized gradient impedance； (c) Normalized curvature. impedance.

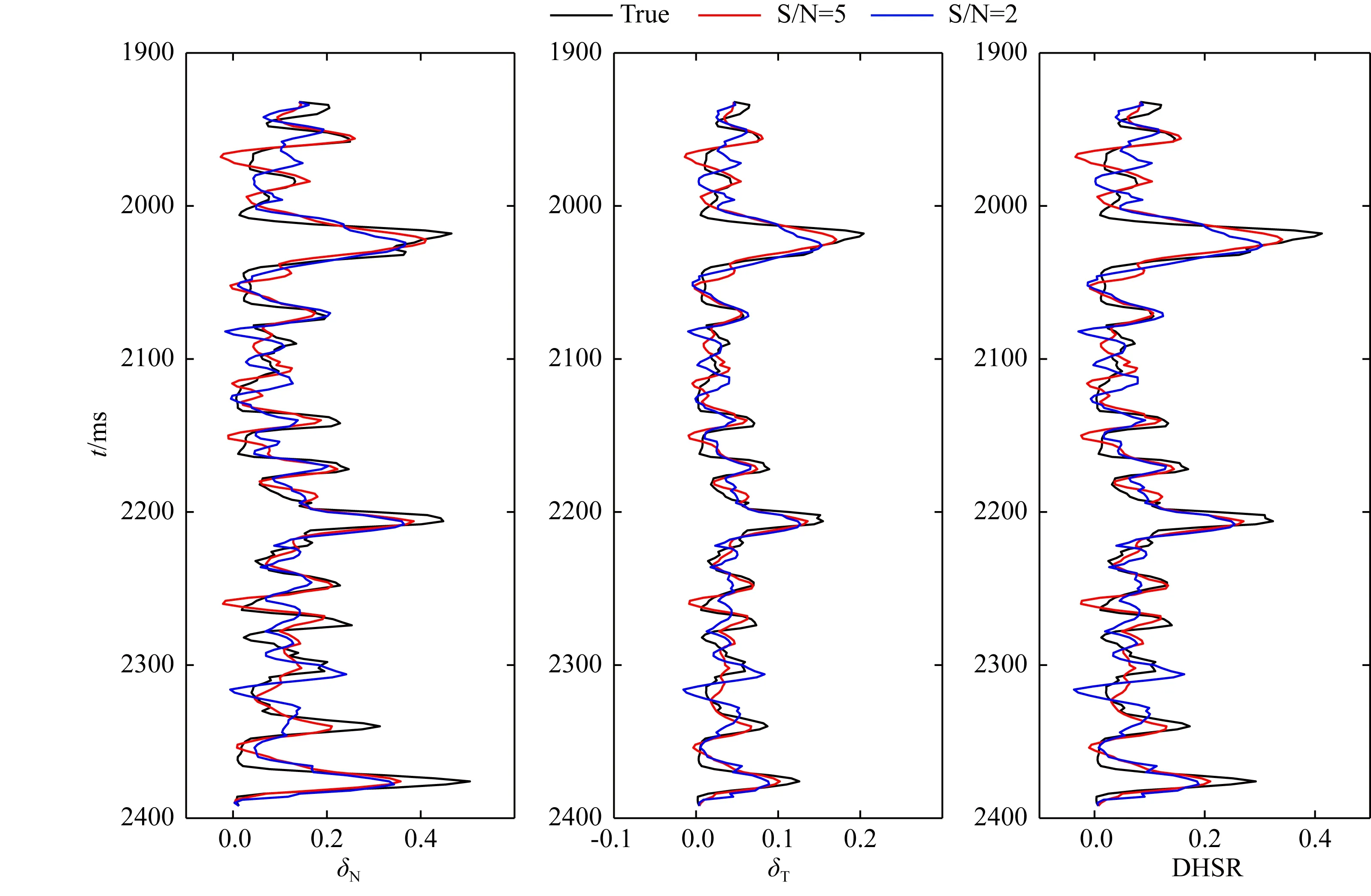
圖7 不同信噪比情況下反演的法向弱度、切向弱度及DHSRFig.7 Inverted normal weakness, tangential weakness, and DHSR for different noise levels

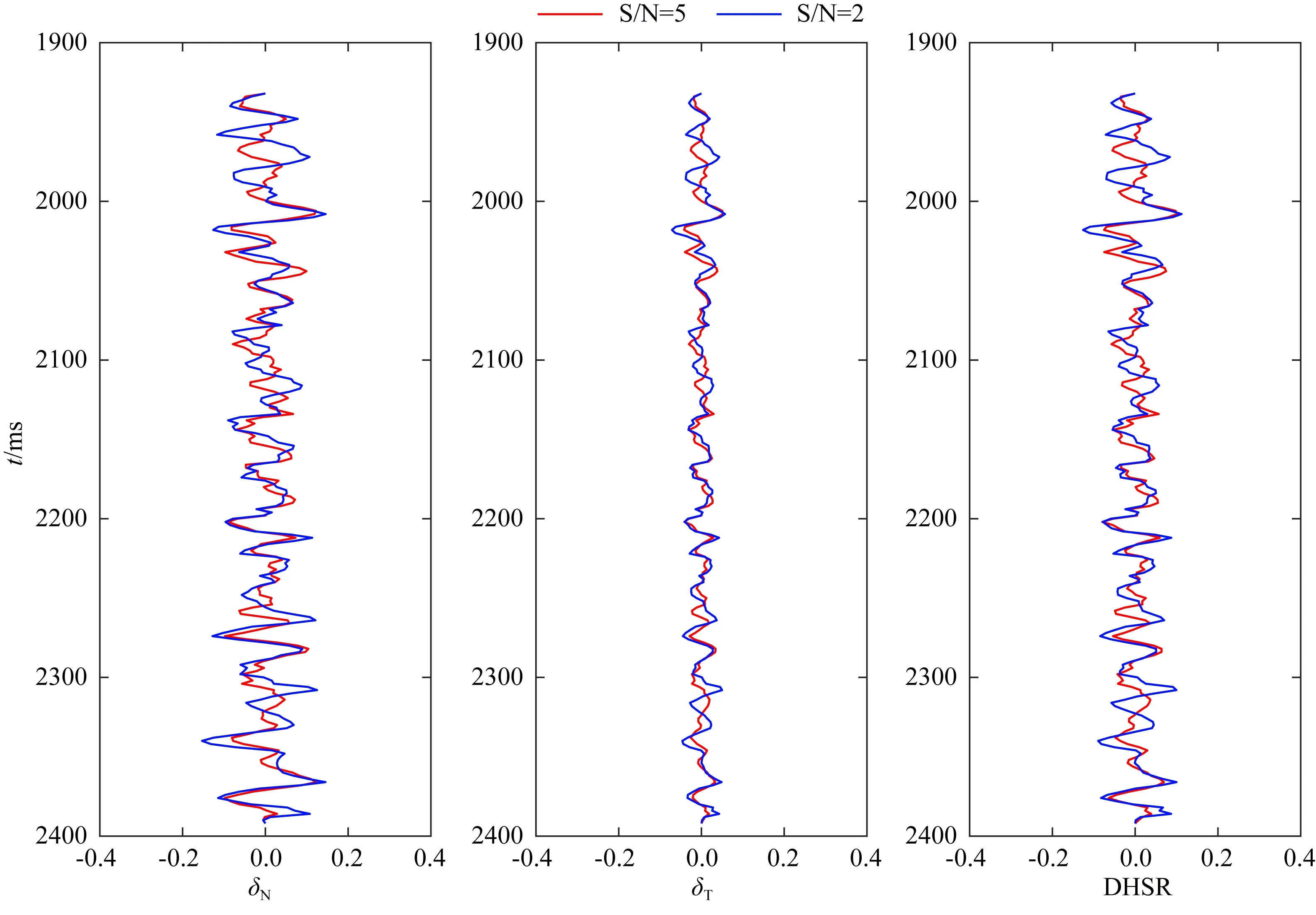
圖8 不同信噪比情況下反演的法向弱度、切向弱度及DHSR與真實值的相對誤差Fig.8 Relative error between inversion result of normal weakness, tangential weakness, DHSR and the true value for different noise levels

3 實際資料處理

研究區域位于四川盆地新場工區，該工區儲層屬超低孔、超低滲型致密砂巖儲層，構造縫較為發育，多為高角度縫和立縫，構造縫多數未充填，對產能貢獻極大，因此可將儲層等效為HTI介質.經過處理后的疊前方位角道集首先被劃分為四個方位，具體方位部分角度疊加方案為22.5°(0°～45°)、67.5°(45°～90°)、112.5°(90°～135°)和157.5°(135°～180°).對每一個方位角道集又分別進行入射角部分角度疊加，得到三個平均入射角，分別為15°(10°～19°)、22°(17°～26°)和29°(24°～33°).利用提出的分方位疊前地震貝葉斯反演方法得到的歸一化截距阻抗、梯度阻抗及曲率阻抗反演結果如圖9所示.最終預測的法向弱度、切向弱度及DHSR結果如圖10所示.提取井旁道地震反演結果與測井曲線進行對比，如圖11所示，可以看出在井旁道的反演結果與井曲線之間盡管存在一定誤差，但總體趨勢與井曲線基本一致.分別計算反演的裂縫參數及DHSR與井曲線的相關系數，反演的法向弱度、切向弱度及DHSR與井中相應曲線的相關系數分別為0.85、0.84、0.85.反演的法向弱度和切向弱度剖面在儲層位置處(黑色橢圓)均表現為相對高值，可靠地指示了儲層的裂縫發育情況；反演的DHSR剖面在儲層位置處也表現為相對高值，在壓裂時應選取DHSR數值相對較小的區域.利用提出的方法預測得到的裂縫參數及DHSR剖面具有較好的橫向連續性，有助于裂縫發育區域及有利壓裂區域的橫向識別.

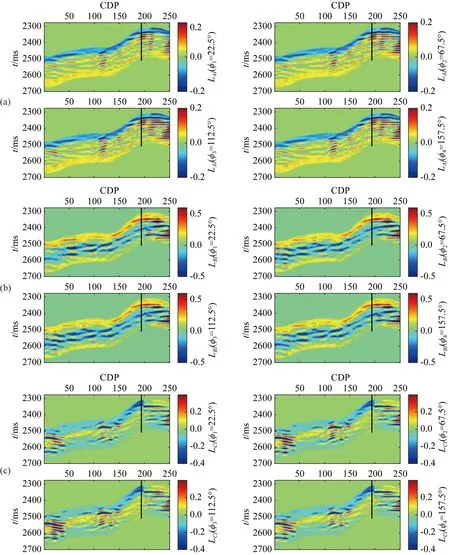
圖9 反演的(a)歸一化截距阻抗，(b)歸一化梯度阻抗及(c)歸一化曲率阻抗(黑線表示井的位置)Fig.9 Inverted (a) normalized intercept impedance, (b) normalized gradient impedance, and (c) normalized curvature impedance (the black line indicates the location of the well)

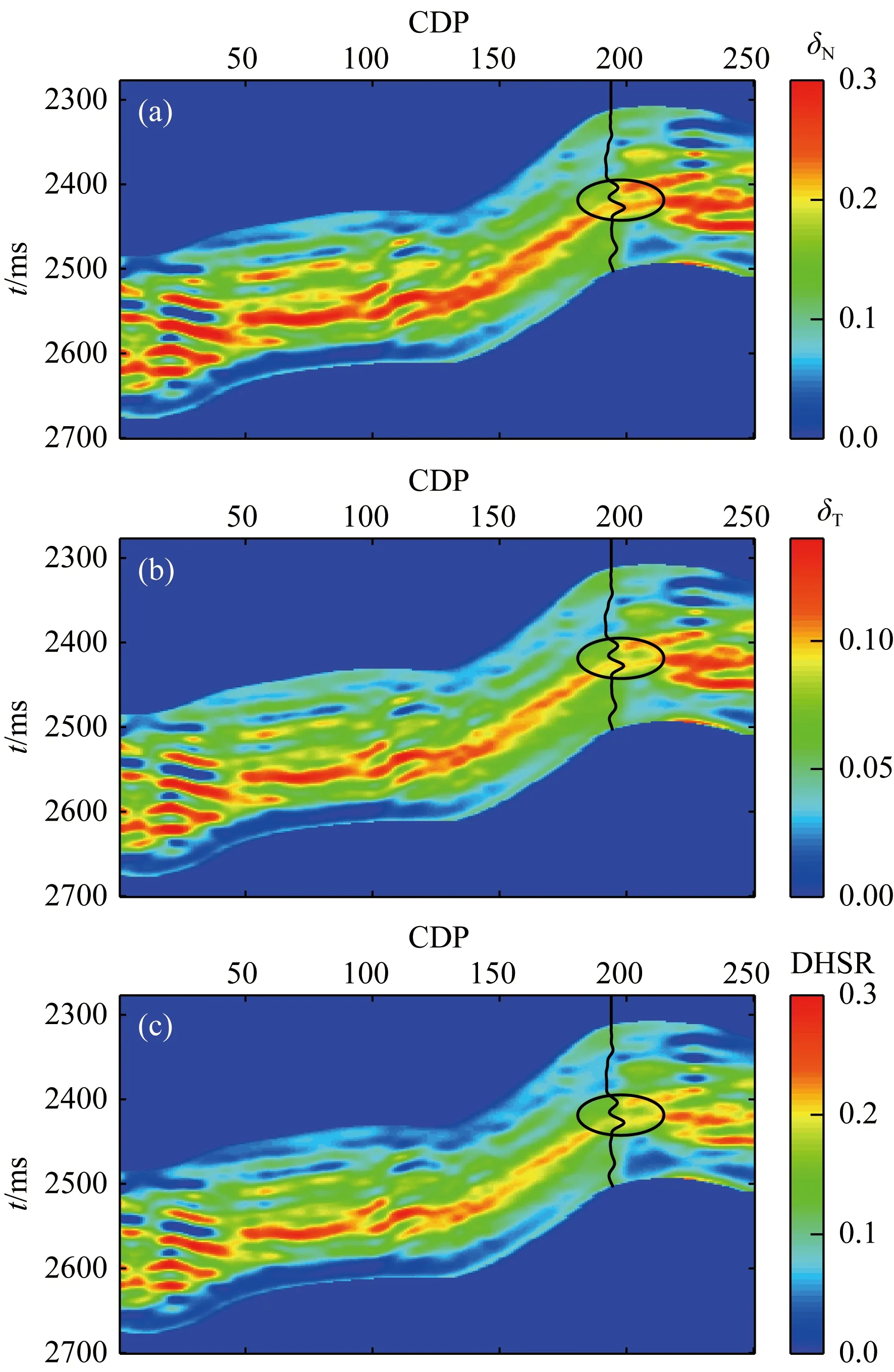
圖10 反演的(a)法向弱度，(b)切向弱度及(c)DHSRFig.10 Inverted (a) normal weakness, (b) tangential weakness, and (c) DHSR

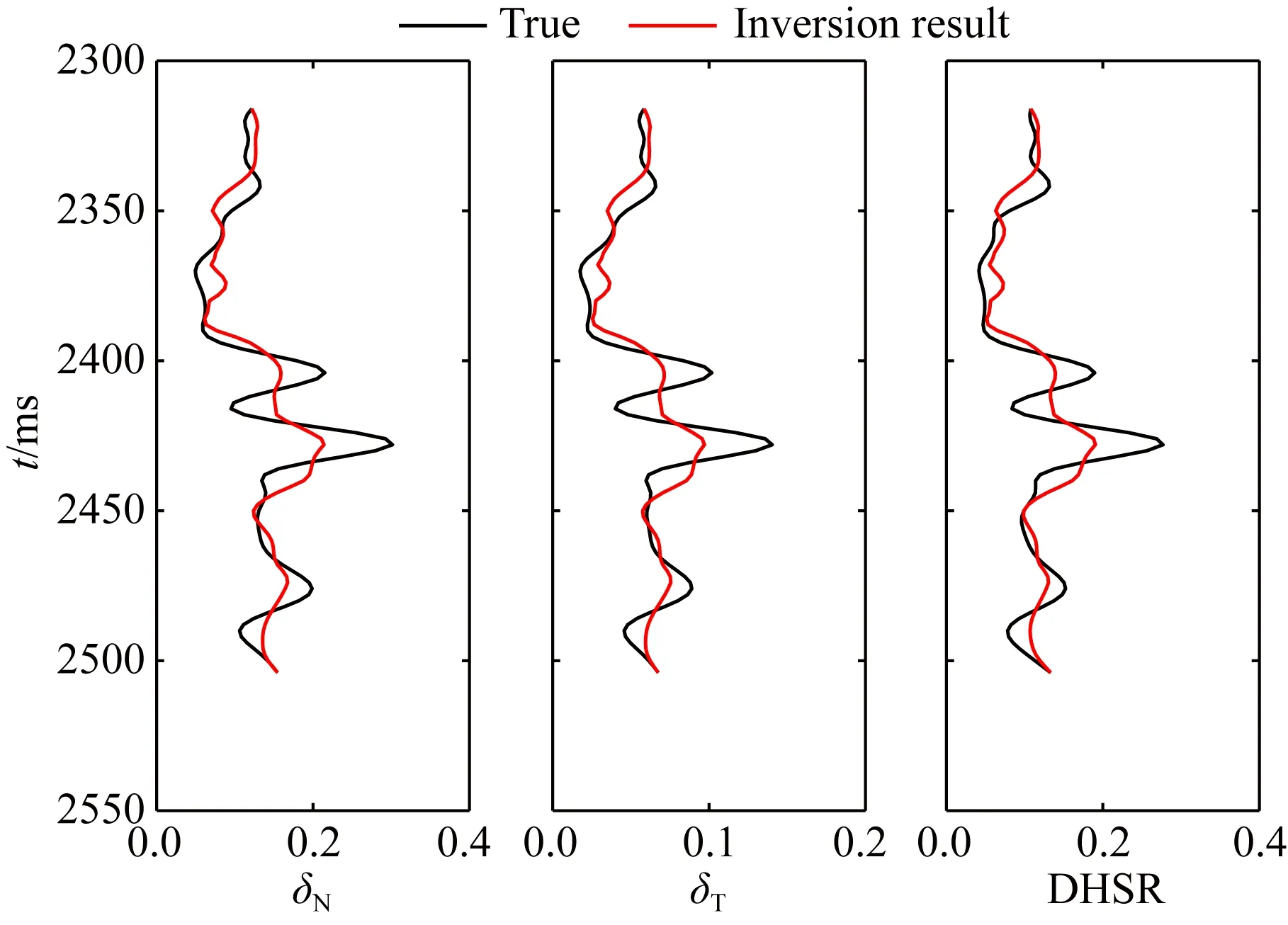
圖11 井旁道反演結果與測井曲線對比Fig.11 Comparison between nearby well inversion results and logging curves

4 結論

裂縫參數及DHSR的準確估測對于地下裂縫預測及水力壓裂具有重要意義，本文提出了一種基于擴展方位彈性阻抗的裂縫參數及DHSR預測方法.首先推導了HTI介質中的擴展方位彈性阻抗方程及傅里葉系數方程，傅里葉系數相關性分析表明，零階傅里葉系數與各向同性參數具有較好的相關性，但與裂縫參數及DHSR相關性較差；二階傅里葉系數與裂縫參數及DHSR具有較好的相關性.通過結合不同的角和分方位疊前地震貝葉斯反演得到截距阻抗、梯度阻抗及曲率阻抗，分析二階傅里葉系數與井中裂縫參數及DHSR的相關性以確定最優的角，進而利用二階傅里葉系數實現裂縫參數及DHSR預測.模型測試表明，即使在信噪比為2情況下，利用提出的方法也能夠得到合理可靠的裂縫參數及DHSR預測結果.實際應用表明，利用提出的方法預測的裂縫參數及DHSR與井中曲線較為符合，且反演剖面具有較好的橫向連續性，有助于裂縫發育區域及有利壓裂區域的橫向識別.