社區快遞智能柜選址布局研究與應用

王亞如，陳 超

（遼寧工業大學 經濟管理學院，遼寧 錦州 121001）

隨著社會經濟的疾速發展，電子商務信息技術的研討開發和推行，消費程度的不斷提高，快遞效能的末端服務成為了人們關注的焦點。末端服務的時間成本、準確度、安全性和快捷性是快遞業服務質量的關鍵因素，社區物流是末端服務中必不能少的一部分，智能柜合理的選址直接關系到客戶對快遞業服務的滿意度，決定著快遞業的發展。丁猛以網點數量最小和固定網點數量的選址模型來解決需求量與取件距離之和最短的問題，并提出大學校園智能快遞柜備選網點的選擇方法。張西莎等對YSL 社區快遞柜的網點分布不均問題，首先采用集合覆蓋模型建模，求出選擇方案，再采用層次分析法對可選方案分析建模。檀竹隔對合肥工業大學實證區域調研，建立集合覆蓋模型與層次分析法兩級優化模型，對快遞自提柜選址模型的合理性和實用性進行實證分析。黃鳳春結合生活實際需要，運用POS 算法得出了模型最優解，助力了快遞公司智能快遞柜的收益最大化目標的實現。

1 研究方法

1.1 重心法

該方法通常被應用在物流運輸領域，指的是一種設置單個倉庫和廠房的方法，其主要考慮運輸貨物量、現有的分銷倉庫等，目的將倉庫或廠房設置在離主倉較近的位置，通過縮短運輸路程來盡量降低運輸費用，從而幫助企業實現利益最大化的目標。該方法的計算公式為：

式中，X0與Y0分別代表重心位置的橫縱坐標，待確定的重心位置的坐標即為（X0，Y0），各個需求地的坐標為（xi，yi），mi代表每個需求地的需求量。

1.2 免疫優化算法

免疫優化算法常用于物流行業，具體可以用于物流倉庫的選址，從而降低運輸成本與倉儲成本。因此本文在建立智能柜選址模型后，引入免疫優化算法完成求解，驗證選址方案的合理性，并得到相應的成本預算。

2 智能柜選址模型構建

2.1 條件假設

假設一：配送網點總容量可滿足顧客需求，配送輻射范圍需求量確定。

假設二：一個需求點僅由一個智能柜中心供應。

假設三：不考慮配送點到智能柜的運輸費用。

2.2 構建模型

該選址模型需滿足距離要求，并從n 個需求點找出智能柜，迎合n 個需求點儲存物品的需求。其目標函數為：

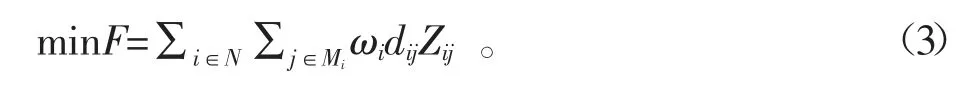
約束條件為：

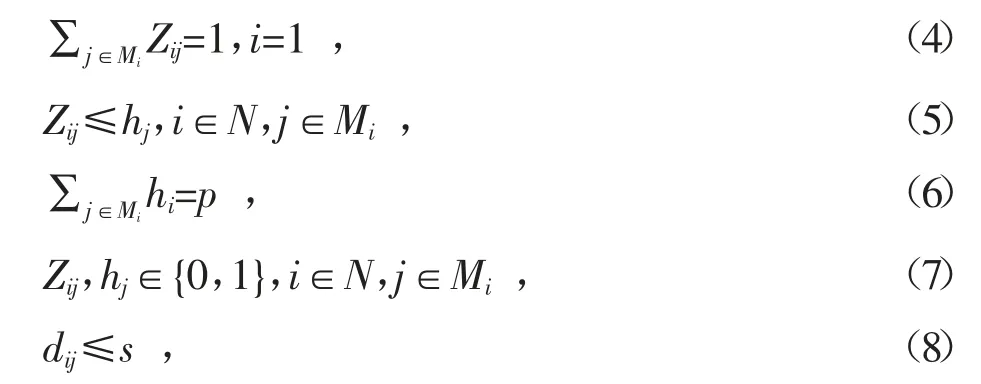
其中，N={1，2，…，n}是所有需求點的序號集合；Mi為到需求點i 的距離小于s 的備選智能柜集合，i∈N，Mi?N；ωi為需求點的需求量；dij代表從需求點i 到離它最近的智能柜j 的距離；Zij為[0，1]變量，代表物流中心與用戶之間服務需求的分配關系，當Zij=1 時，代表由智能柜j 供應滿足需求點i 的需求量；否則Zij=0；hj為[0，1]變量，當hj=1 時，表示智能柜儲存點選取j 是合理的；s代表智能柜與需求點的距離上限。

式（4）保證每個需求點只能由一個智能柜儲存點服務；式（5）確保需求點的需求量只能被設為該智能柜供應；式（6）規定了被選為智能柜的數量為p；式（7）表示變量Zij和hi是[0，1]變量；式（8）保證了需求點在智能柜儲存的范圍內。

2.3 計算步驟

第一步，抗原識別，即分析實際問題之后建立目標函數，設立約束方程。

第二步，得到初始方程解，即確定初始選址方案。

第三步，計算抗體親和度，其公式為：

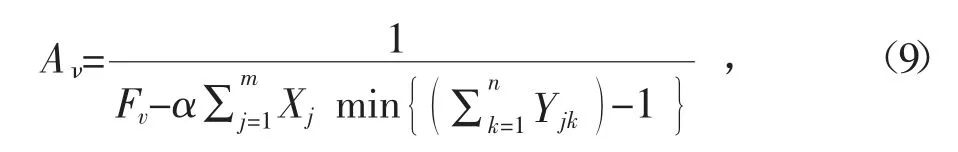
式（9）中，Aν表示親和度，Fv表示目標函數，代表基于距離的懲罰值，若得到的結果較大代表備選中心與需求點距離過大，為了保證其適用性，需要降低其被選中的概率。

第四步，判斷是否滿足終止條件，即計算結果符合終止條件或迭代次數，則可直接輸出結果，反之，需要調整變量值繼續計算。

第五步，抗體群多樣性評價，即利用該公式：

計算其抗體濃度與親和度，濃度過高則證明抗體有效，可直接消滅抗原，但并不是濃度值越大越好。

式（10）中，Cv表示抗體濃度，M 為種群中抗體總數，Xij為[0，1]變量。

式（11）表示如果抗體i 與抗體j 的相似程度大于設定的閾值T，則記Xij為1，反之為0。

繁殖概率計算公式如下：

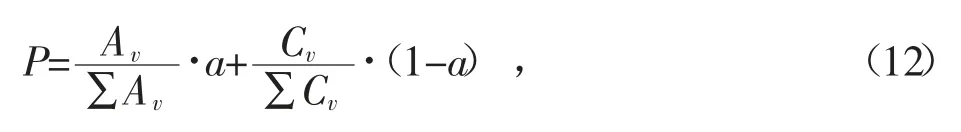
式（12）中，P 表示個體繁殖率，Av表示抗體的親和度，Cv表示抗體的濃度，a 表示多樣性評價參數。根據個體繁殖率進行排序，選取排名靠前的抗體形成父代群，更新記憶庫。

第六步，免疫操作，包括免疫的選擇、交叉、變異。

第七步，更新種群，得出結論。即保留親和度較好的個體，將個體繁殖率較低的抗體替換為經變異操作新生成的抗體。

3 實例研究

小區總占地面積5.28 萬m2，總建筑面積26.82 萬m2，住宅面積18.99 萬m2。小區共17 棟住宅8 棟小高層（包含1棟物業樓）和9 棟高層組成，具體戶型圖如圖1 所示。為了營建一個自然諧和的宜居環境，結合自然與人文的小區設有隔音屏、綠化帶，高達30%的綠化率。園區內有高檔休閑會所與780 m2大型幼兒園以及地下車庫。

圖1 社區戶型圖

通過表1 可以看出每棟樓的住戶數量，并根據統計學原理可知，每棟樓的快遞需求量大體相似，因此假設每戶在同一時間范圍內取件數量為1，則可用住戶數量代替快遞需求量。

表1 需求量與坐標基本情況

3.1 基于重心法進行初步選址

首先構建參照坐標，為了簡便起見，將該社區的地理坐標作為參照坐標，相關參數參考該小區總平面規劃圖，并作處理，社區坐標分布圖如圖2 所示。

圖2 社區坐標分布圖

利用重心法模型的計算公式，將表中的數據代入公式（1）、公式（2），得X0=121.1406，Y0=41.13065。故重心坐標為（121.1406，41.13065），如表1 中6 號樓坐標所示。

采用重心法縱然可以得到模型中的理論選址地點，但考慮實際中的經濟成本、取件空間等諸多因素，因此該坐標只能作為參考，還需在附近選取幾個備選地址。根據本研究首先將選址地點統一羅列出來作為備選，其次根據居民區實際情況運用免疫算法對備選方案進行計算與決策。經實地考察，得到3 種備選方案：分別是重心點的6 號樓，及根據三角形穩定性實地距離測量選中的11 號樓和15 號樓。

3.2 基于免疫優化算法模型求解

利用MATLAB R2015b 軟件，通過對參數的多次調試，最終設置種群規模為10，記憶庫容量為10，最大迭代次數為50，交叉概率為0.5，變異概率為0.4，多樣性評價參數為0.95，參數設定之后輸入小區中各物流節點的坐標、建設及經營成本、進出貨情況等各項數據，通過多次迭代計算后，得出的免疫算法收斂曲線如圖3 所示。

從圖3 中可以看出，在12 次迭代時抗體適應度值不再發生大范圍變化，而是趨于范圍性穩定，證明免疫優化算法在得到最優解的同時，其達到收斂的時間也比較短，能夠有效解決實際配送問題，并滿足居民需求。

圖3 免疫算法收斂曲線

為了更加直觀地看出選址情況，特將經緯度轉換為通俗易懂的大地坐標，一方面可精確計算各地址之間的距離間隔，另一方面能夠清楚地觀察到配送中心位置與配送情況。如圖4 所示為物流配送中心分布及其負責的配送服務情況，方框選定的圓點代表選擇建設物流配送中心的樓號，其負責配送的需求點以細線的形式連接起來。

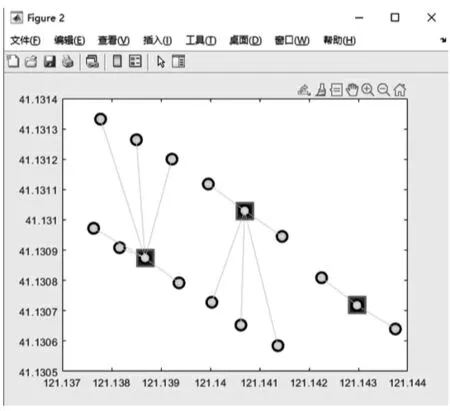
圖4 智能柜選定及其配送情況

3.3 選址結論

通過免疫優化算法計算得到的最優解為5 號樓，12 號樓，15 號樓。結合重心法，根據實地考察小區的實際空間，5 號樓和6 號樓之間是休息涼亭，其為智能柜建造提供了有利條件；11 號樓和12 號樓之間是車輛、居民出行道路，符合智能柜的選址條件；15 號樓有個小型超市并且是南門出入口，符合智能柜選址條件。

4 結束語

綜上所述，在充分考慮解決實際問題的基礎上，引入了重心法與免疫優化算法，通過結合實例最終選定了該小區的智能柜位置，對促進居民的生活便利性與提高物流配送效率均有重要意義。隨著互聯網技術的持續升級與應用，快遞業務日漸倍增，解決最后1 km 的配送問題才是突破行業瓶頸的有效途徑，精準的智能柜選址是提升居民取件便利性與企業效益的最佳選擇。