利用信息技術實現極限思想的可視化

李金良 孫梅芳

(安徽省蚌埠田家炳中學，安徽 蚌埠 233010)

1 引言

在高中物理教學中運用極限思想,主要解決變化率和積累等物理問題。就高中生對數理結合的認知能力現狀而言,還處于一種較低層次,對極限思想的理解比較模糊,借助信息技術將極限思想可視化,可幫助學生將思維形象化,有利于學生深刻理解極限思想。

2 信息技術助力可視化教學的意義

信息技術是指用于處理信息、管理信息所采納的科學技術的總稱。應用于物理教學中的信息技術是指一些軟件技術和硬件技術的綜合應用,包括電子技術、軟件技術、網絡技術、感測技術、控制技術、光刻技術、顯示技術等,是對聲音、圖像、文字、數字和各種信息進行獲取、加工、處理、儲存和使用的技術。

可視化教學體現了有效的“教”與有效的“學”的本原,即可視化教學具有兩層含義:一是讓教師看見學生的“學”,教師能清楚看到學生學習遇到的障礙等;二是讓學生看見教師的“教”,即教師的引導和幫助作用,促使學生自主學習。本文所述的可視化是指應用信息技術手段助力學生的學習，實現極限思維過程可視化,其意義在于幫助學生克服思維障礙,給予必要的技術支持,幫助學生體驗物理學情境,培養抽象思維能力,提高學習實效。

3 中學物理中的極限思想

極限思想是微積分在中學物理中的體現,是指用極限觀念分析和解決問題的一種數學思想,是近代數學和物理中的一種重要思想方法。極限思想在中學物理教學中也常稱為微元法,也就是把研究對象分為無限多個無限小的部分(微元),達到“化整為零”“化曲為直”“化變為恒”的目的,取有代表性的極小部分進行分析,進而實現從局部到整體綜合起來分析問題的科學思維方法。

中學物理用到的極限思想在高中必修教材中的主要體現如下。

(1)物理概念:瞬時速度、瞬時加速度、瞬時功率、圓周運動中的線速度和向心加速度等。如求解瞬時速度的方法是用極短時間內的平均速度代替瞬時速度，線速度的方向沿切線方向、向心加速度公式的推導等都用到了極限思想。

(2)利用圖像面積求解物理量。例如利用v-t圖像求位移x，利用F-l圖像求功W,彈性勢能的表達式推導等,這是一種“化整為零”的極限思想,也是一種“化變為恒”的極限思想。

(3)曲線運動下重力做功公式推導、向心加速度公式的推導等體現了一種“化曲為直”的極限思想。

除此之外,極限思想在選修教材中也有很多體現,比如瞬時感應電動勢、電勢能、電流元、單擺、利用i-t圖像求電荷量q、利用F-t圖像求沖量I等。可見,極限思想涉及中學物理中多個重要的知識模塊,能否理解及靈活運用極限思想處理物理問題是學好中學物理的關鍵。

4 應用Visual Basic編程制作課件，助力極限思想可視化

學生進入高中階段不久,在學習“運動的描述”中 “平均速度和瞬時速度”“打點計時器測速度”時首次接觸到極限思想,之后在第二章“勻變速直線運動的位移與時間的關系”一節中,利用v-t圖像求位移再次用到極限思想處理具體問題。由于極限思想中逐步分割的思維過程很難通過語言進行形象化表達，使學生有直觀的感受,不少學生對極限思想認識模糊,導致后續學習問題頻出。

鑒于上述原因,筆者嘗試利用計算機編寫程序制作課件,通過人機交互的動態畫面讓學生感受極限思想的過程與方法,幫助學生深度理解極限思想。本文中課件采用VB程序編寫,VB是Visual Basic的簡稱。據百度百科介紹:“Visual Basic是微軟公司開發的一種通用的基于對象的程序設計語言,為結構化的、模塊化的、面向對象的、包含協助開發環境的事件驅動為機制的可視化程序設計語言。”VB語言最大的特點就是簡單,面對一些小程序選擇用VB編寫,相對來說會更輕松、更快捷。

4.1 從割圓術走進極限思想

三國時期的數學家劉徽首創割圓術，用圓內接正多邊形的面積(或周長)去無限接近圓面積(或周長)，以此求得圓周率，體現了極限思想的精髓,圖1分別展示了圓內接正四、十、四十邊形的情況。通過上述多次分割,用圓內接正多邊形的面積(或周長)逐漸去逼近圓面積(或周長),可讓學生初步感知極限思想。

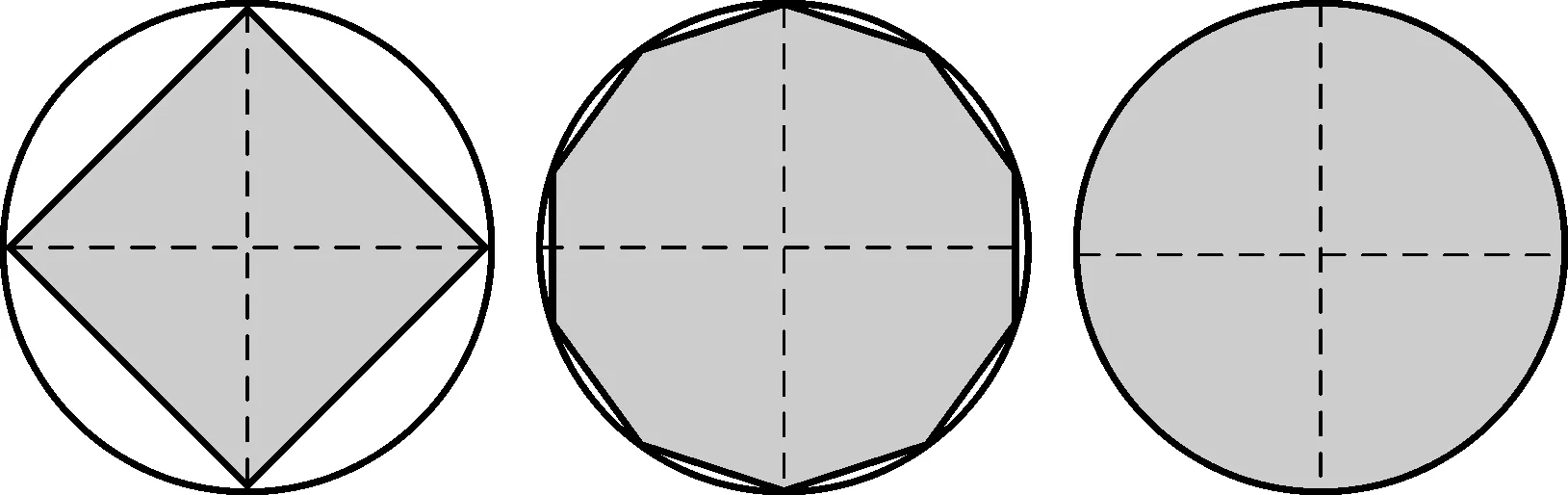
圖1

4.2 用v-t圖像求位移，再次認識極限思想

在勻變速直線運動的教學中，從v-t圖像求位移，運用了“化變為恒”的極限思想。勻變速直線運動物體的v-t圖像如圖2中斜線所示,其關系式為v=6+0.4t，若將其分割為10段,則每段的橫坐標分別為2，4，6，8……10,結合上述關系式即可算出圖線上每個分割點的縱坐標,據此就可以繪制出10個小矩形,乃至更多小矩形(圖3)。

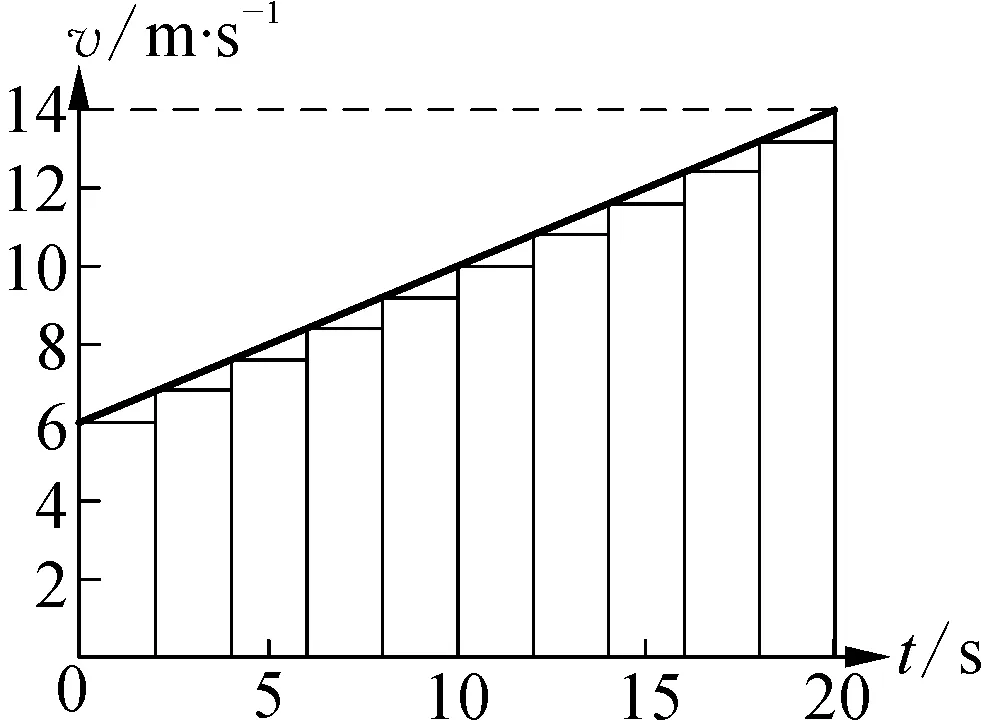
圖2

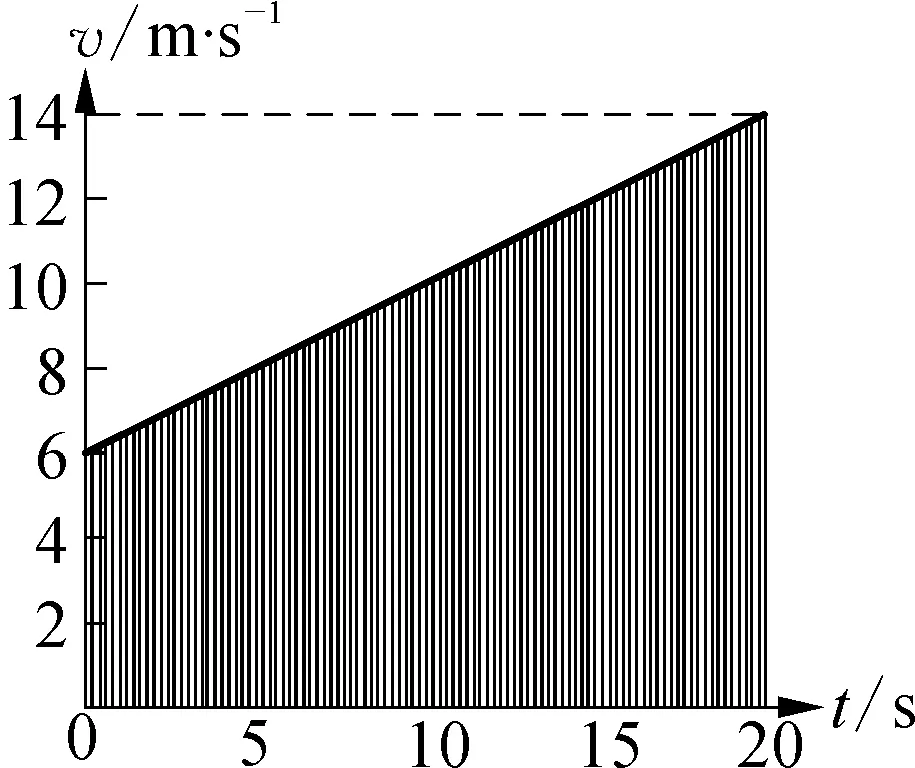
圖3

圖像無限分割的漸進顯示技術能帶給學生很好的直觀體驗,再結合數據計算來進一步說明極限思想的科學性和嚴謹性。計算小矩形面積之和的方法之一是用等差數列的求和公式,程序中就采用了該方法計算這些小矩形面積之和。在圖2中,10個小矩形的面積之和為192,與梯形面積200間的相對誤差為4%;如圖3所示，當小矩形增加到100個時,這些矩形的面積之和為199.2,與梯形面積間相對誤差為0.4%。容易看出,分割的段數越多,所有小矩形的面積之和就越接近于梯形面積,如果分割的段數為無窮多,小矩形的面積之和就等于梯形的面積,也就是整個運動的位移了。

4.3 從“平均速度到瞬時速度”深度認識極限思想

研究物理問題常常遵循由簡到繁的原則,本文以瞬時速度為例進行分析，瞬時加速度、瞬時功率、瞬時感應電動勢等與此類似。

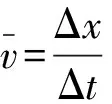
設變速直線運動位移與時間關系滿足x=8t+4t2,其0時刻的瞬時速度為8 m/s。圖4、圖5、圖6分別展示了時間間隔為1 s、0.1 s、0.01 s 內平均速度的情況。從課件截圖的數據可以看出,因為這是一個加速運動,平均速度均大于0時刻的瞬時速度,但時間間隔越短,平均速度越小,但不會無限減小,而是逐漸地趨向于8 m/s,這就是0時刻的瞬時速度。也就是說,當時間間隔足夠小時,求得的平均速度就是該點的瞬時速度。另外,圖中的細線也反映了平均速度過渡到瞬時速度的過程,當時間足夠短時,細的割線就變成了0時刻x-t圖像的切線,利用切線的斜率求出的平均速度也變成了0時刻的瞬時速度。

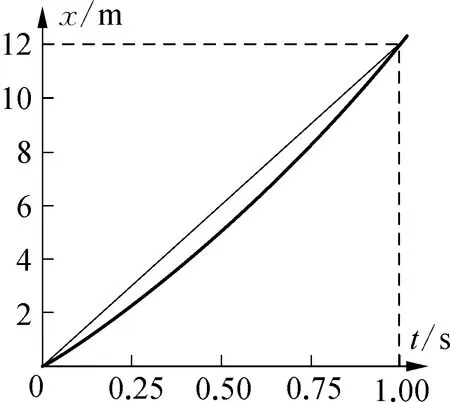
圖4

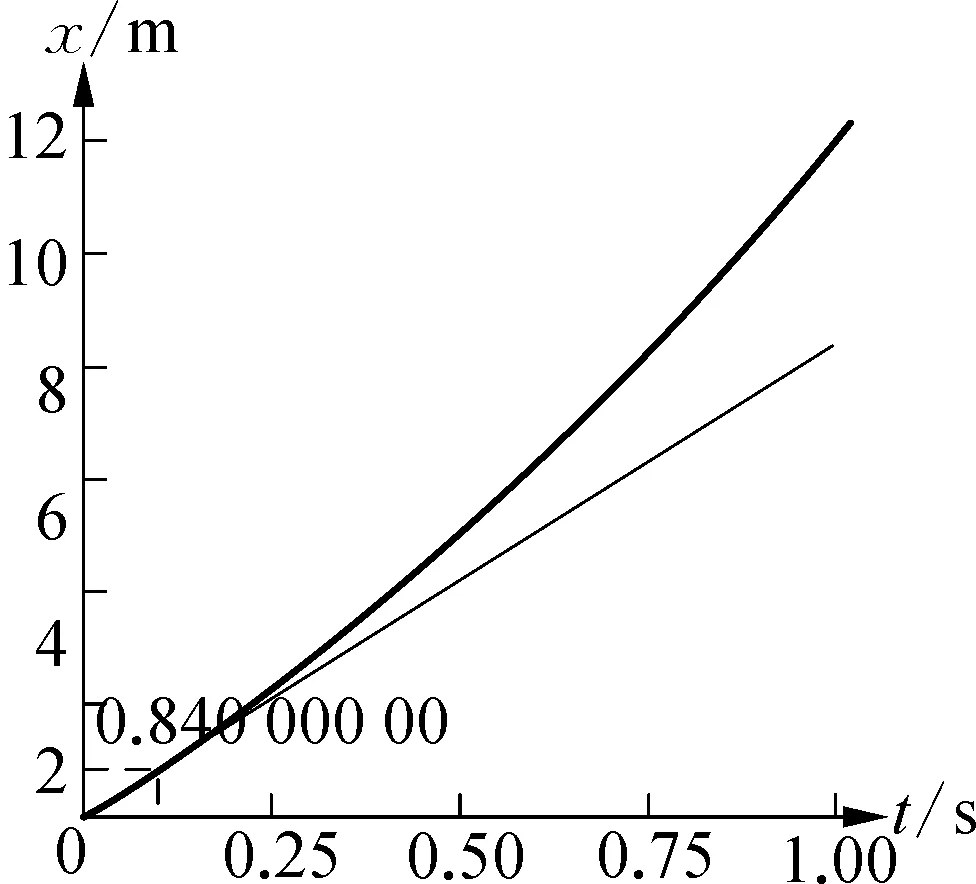
圖5

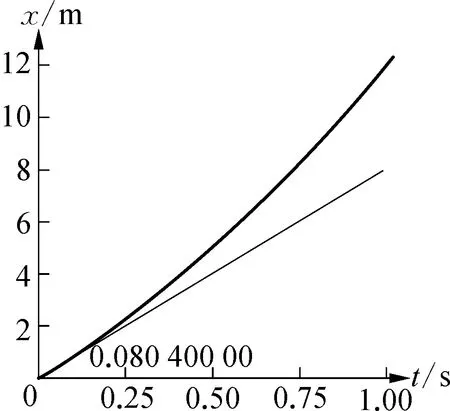
圖6

4.4 “化曲為直”強化對極限思想的認識

圖7

圖8

圖9

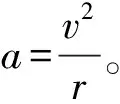
5 結語

極限思想是一種重要的科學思想,運用極限思想解決物理問題既能加深學生對物理概念、規律的理解,又能提高學生的思維能力和解決問題的能力。在物理教學中,體現極限思想方法的應用很多,教師應站在培養學生核心素養的高度，運用信息技術手段, 滲透極限思想方法，為學生形成物理觀念打下堅實基礎。