基于動態貝葉斯網絡的低慢小目標威脅評估

李輝強,王 毅,李麗亞

(華北光電技術研究所,北京 100015)

1 引 言

威脅評估是以目標的距離、速度、高度等狀態信息,敵我屬性、設備類型等屬性信息,以及我方防御部署、地形等當前態勢信息作為基礎,構建的高層次的信息融合技術。威脅評估反映了敵方目標對我方的威脅程度,是指揮控制系統中重要的一部分,是指揮員在軍事行動中進行指揮決策的一個重要環節。

低慢小目標,全稱是“低空、慢速、小型”飛行目標,在通常情況下,將符合全部或者部分如下特征的各種小型航空器和空飄物統稱為低慢小目標:1)飛行高度不高于1000米；2)飛行速度不大于200 km/h；3)雷達反射面積不大于2m2。低慢小目標具備 “低空超低空飛行,飛行速度較慢,不易被偵察發現”等特點[1]。對于重大活動的安保,由于其通常在人口和建筑物密度高的政治經濟中心舉辦,周圍均為高樓林立、電磁信號繁雜,環境十分復雜,在處理低慢小目標威脅上,總是面臨著難以探測、難以跟蹤、難以處置的“三難”境地。這對防控系統提出了巨大的挑戰。目標威脅評估作為低慢小目標防控系統在作戰流程中的一個關鍵環節,其效能的高低對于防控系統的整個能力有著十分重要的作用。因此如何提升防控系統對低慢小目標的威脅評估能力是一個重點研究方向。

目標威脅評估中經常使用的理論和方法主要有多屬性決策、模糊集、粗糙集、神經網絡[2]、貝葉斯網絡、支持向量機、排序法、基于知識推理等,或者是上述多種方法的有機結合。近幾年來以低慢小目標為對象進行威脅評估研究的文獻也越來越多。其中基于貝葉斯網絡、神經網絡、云模型理論的低慢小目標威脅評估方法逐漸成為研究的熱點[3]。

本文主要研究并提出了一種基于動態貝葉斯網絡的威脅評估模型,并對該威脅評估模型進行建模仿真分析。

2 貝葉斯網絡原理

貝葉斯網絡是貝葉斯方法的擴展,在人工智能領域,貝葉斯網絡是解決不確定問題時最常用的工具,它將概率統計用于復雜系統中的不確定性推理[4],是目前不確定知識和概率推理理論中最有效的理論模型之一[5]。

貝葉斯網絡主要由兩部分組成:一是網絡結構,通常采用有向圖來描述。在這個網絡結構中,節點用于標識某一個屬性,可以用來標識低慢小目標威脅評估模型中的某一個目標屬性；節點之間的聯系,用于標識節點之間的聯系,可以用來標識低慢小目標威脅評估模型中不同目標屬性之間的因果關系[6]。

隨著貝葉斯網絡被廣泛應用于各個領域中,進行各種各樣不確定性推理,其本身的一些缺陷也隨之逐漸暴露。尤其是在隨著時間變化的動態系統中,其許多方法無法滿足前后時刻間關聯性和互補性的需求。在此基礎上,通過將原有的貝葉斯網絡與時間要素關聯,提出了動態貝葉斯網絡(DBN),而之前的貝葉斯網絡則被稱為靜態貝葉斯網絡(SBN)。

動態貝葉斯網絡(DBN)是在靜態貝葉斯網絡(SBN)的基礎上,與時序信息相結合而構成的[7]。對于一個靜態貝葉斯網絡,以一個隨機變量集X={X1,X2,…,Xn} 來表示網絡中的各個節點,構成屬性集。假設這個屬性集里的每一個屬性都是是隨時間變化而變化,則在t時刻,可以用Xi[t] 來表示在t時刻時,網絡內某一個屬性Xi的值,那么可以定義X[t] 是隨機變量Xi[t] 的集合。為表示全過程中網絡結構變化軌跡的度,在隨機變量X[0]UX[1]U…上進行概率分布[8]。隨機變量X全過程中都符合馬爾可夫鏈要求,即:

P(X[t+1]|X[0],…,X[t])=P(X[t+1]|X[t])

除此之外,動態貝葉斯網絡還包含有另一個假設——齊次性,即在整個網絡在時間進行變化時,其轉移過程中的轉移參數不隨時間的變化而發生變化。

基于上述的幾個假設,可以將動態貝葉斯網絡簡單分為兩個部分,即先驗網絡和轉移網絡兩部分。其中先驗網絡B0,用于表示初始時態X[0] 的分布；轉移網絡BT,用于表示所有時間t上的轉移概率P(X[t+1]|X[t])。

綜上所述,動態貝葉斯網絡的結構和結構參數并不會隨著時間的推移發生變化,而是網絡所包含的樣本數量,或者說觀測數據則會隨著時間的推移而發生變化。

3 低慢小目標威脅評估模型的構建

通過上述對貝葉斯網絡、動態貝葉斯網絡的分析可知,建立基于貝葉斯網絡的低慢小目標威脅評估模型可以簡單分為兩部分——模型拓撲結構的建立和模型參數的確定。通過對低慢小目標偵測處置系統組成、作戰任務的分析,確定合理的節點、建立合理的模型拓撲結構；對低慢小目標偵測處置系統各設備的功能性能進行評估、對系統作戰流程進行分析,確定模型內各個節點之間的參數。在完成模型結構和模型參數的建立后,還需要進行結構的調整和參數的優化,使得整個威脅評估模型更加貼近真實狀態。

3.1 目標威脅屬性提取

在防控系統對低慢小目標進行威脅評估時,為了能夠確定低慢小目標的威脅等級,需要精確地掌握低慢小目標的多種屬性。為了構建針對低慢小目標的貝葉斯模型,選取合適的低慢小目標威脅屬性集,成為其中關鍵的一個步驟。為了實現這一步驟,需要對低慢小目標的威脅進行多方面的考慮,大致如下。

3.1.1 目標機動特性

目標的機動特性包含以下幾點:

1)目標距離,是指目標距離我防御區的直線距離,根據任務要求,可以將我方的重點防御區向外擴展并分為三級防御圈,根據目標的距離,將目標的距離劃分為處于我方某一級別防御圈內；

2)目標速度,目標的飛行速度越大,則進入我方防護區域更快,留給我方處置節點的窗口時間更短,目標的威脅也隨之增大；

3)目標高度,目標高度越低,越容易進入雷達的盲區、無線電偵測系統越難從復雜電磁環境中偵測到目標,目標被發現的困難也就越大,同時對于處置節點來說處置死角增加、處置難度增大。

3.1.2 作戰場景需求

從系統的作戰場景需求分析,對低慢小目標的威脅等級進行評估時主要考慮以下因素:主要目標類型,系統保護對象。以系統的作戰場景需求為對象進行分析的目的主要是,判斷防控目標能否對我方造成嚴重威脅,或者是在不同的場景下,針對所需保護目標對象的不同,防控系統的主要防控目標類型也不同。例如,在軍隊駐地、黨政要地等城市區域內常態化部署的場合下,多旋翼是低慢小目標防控系統面對的最常見也是最主要的防御目標對象；對于核電站水壩、訓練基地等野外條件下的重要場所,固定翼無人機則是低慢小目標防控系統的主要防御目標類型。同時,不同類型的目標,其飛行特性不同,我方防控系統對其的探測和處置能力也不同,例如與無人機相比,以氣球為代表的空飄物,其飛行速度較低,在低空時容易被混淆為鳥類,更難被坦誠處置。在本文,從作戰場景需求出發,主要將低慢小目標的目標類型作為威脅屬性進行考量。

3.1.3 復雜環境下我方防控系統對低慢小目標的處置能力

在以城市為背景的復雜環境下,我方防控系統對低慢小目標的探測和處置能力會受到所部署環境的影響。在不同方向上我方防控系統的探測處置能力會因為樓層遮擋、附近移動網絡基站干擾等因素而急劇下降,因此在復雜環境下對我方防控系統的處置能力要根據實際部署場景進行分析。在本文,將我方防控系統對目標的處置能力也作為一個重要的目標威脅屬性進行考慮。

在低慢小目標威脅模型中,目標的各個威脅因子的權重是不同的,因此可以采取融合處理的方式對低慢小模型中目標的威脅因素進行處理,提高系統的可靠性,盡量避免出現個別因素導致威脅評估模型結果出現重大波動。

3.2 拓撲結構的建立

首先是根據貝葉斯網絡的構建方法,建立低慢小目標的威脅評估先驗網絡模型。圖1是低慢小目標威脅等級評估的先驗模型。

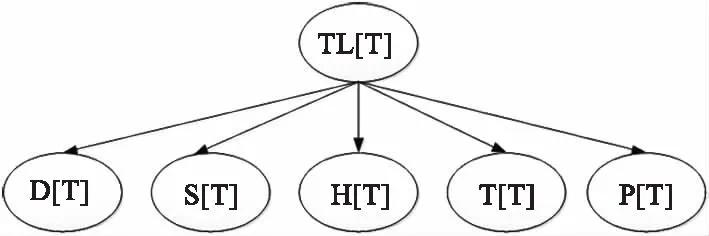
圖1 低慢小目標威脅評估的先驗模型Fig.1 Prior Model of LSS Target Threat Evaluation Based on Expert Experience

其中D為目標距離,S為目標速度,H為目標高度,T為目標類型,P則反映了防控系統對低慢小目標的處置能力。各變量的取值范圍如下。

1)目標距離(D){一級圈內(T1)、二級圈內(T2)、三級圈內(T3)、三級圈外(T4)}；

2)目標速度(S){18m/s以上(R1)、3m/s～18m/s(R2)、0～3m/s(R3)}；

3)目標高度(H){100m以上(S1)、40m～100m(S2)、40m以下(S3)}；

4)目標類型(T){多旋翼(L1),固定翼(L2),空飄物(L3)}；

5)我方處置能力(P){有效處置(P1)、無法處置(P2)}；

6)目標威脅等級(TL){高(TL1),中(TL2),低(TL3)}。

根據動態貝葉斯網絡模型的原理,低慢小目標的威脅評估動態模型是在已經建立的目標威脅評估先驗模型基礎上[9],以時間作為自變量,構建一個簡單的基于相鄰時間的關聯關系,用來表現在進行低慢小威脅評估時各評估因素之間動態的聯系以及變化規律。基于時間的低慢小目標威脅評估轉移模型如圖2所示。

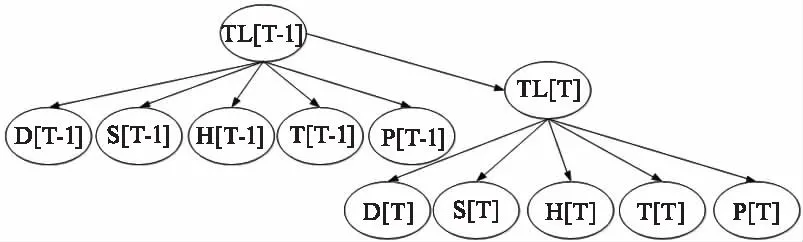
圖2 基于時序的低慢小目標威脅評估轉移模型Fig.2 Transfer Model of Threat Evaluation Bayesian Network Based on Time Series

3.3 條件概率矩陣

在低慢小目標威脅評估模型中,條件概率矩陣反映了低慢小目標防控系統中的經驗,體現出了現實中防控系統對低慢小目標威脅進行評估過程中各個因素之間的關聯。結合對現有低慢小防控系統在歷次演習和任務執行過程中積累的相關數據的分析,根據目標特性以及我方處置能力對目標微威脅等級進行推理的條件概率矩陣如表1所示。

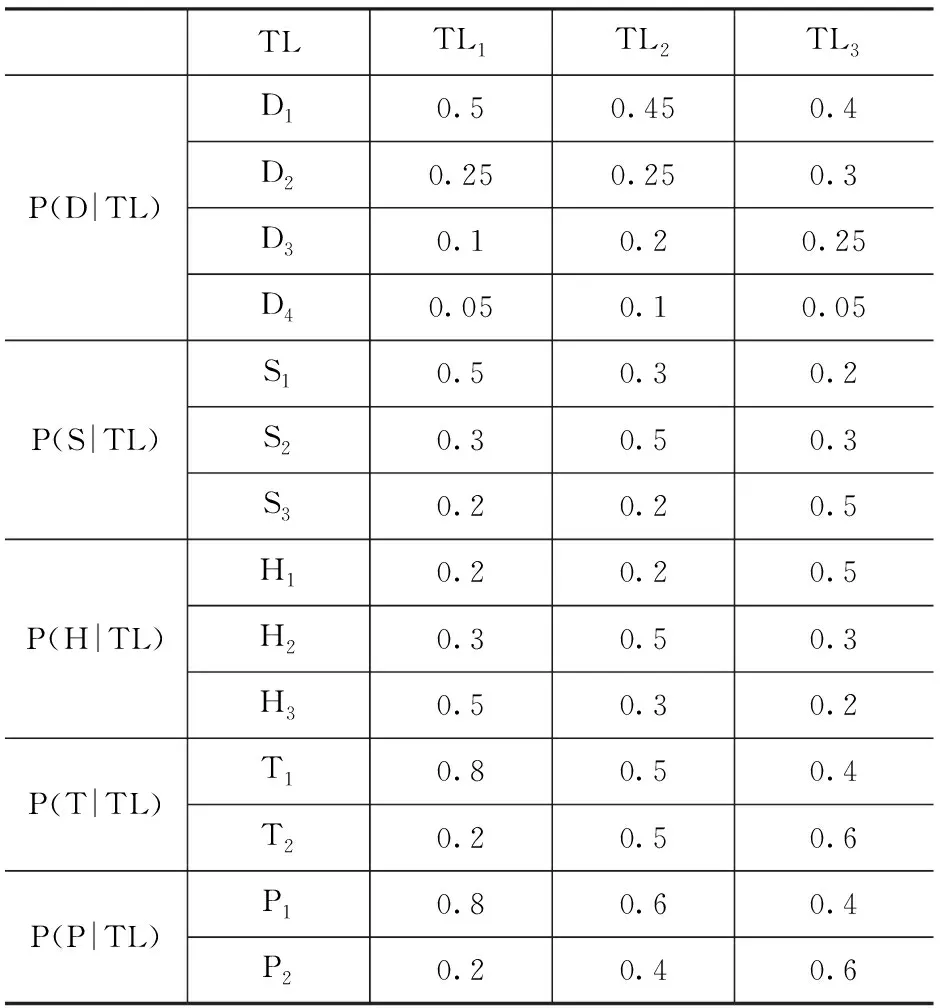
表1 條件概率矩陣Tab.1 Conditional probability matrix

由于人為的主觀因素對于條件概率矩陣的確定具有很大的影響,因此可以采用參照歷史數據和基于數理統計相結合的方法對樣本數據進行反復調試,從而提高對低慢小目標威脅等級評估的可信度。

4 仿真實驗

以上文分析的目標屬性特點、作戰場景需求等,建立一個低慢小目標威脅評估系統,且想定預先沒有關于低慢小目標的空情信息。通過對現有的低慢小防控系統在歷次演習和任務的執行過程中積累的相關數據進行分類計算和統計,可以將低慢小目標威脅等級的先驗值設定為P(TL)=(0.251,0.312,0.437)。

首先進行低慢小目標威脅評估系統結構的初始化和基本參數的初始化,完成系統的準備工作。當我方防控系統的探測設備采用主動或被動方式捕獲到低慢小目標后,系統中各個網絡節點的信息開始時刻更新,系統也開始利用數據進行推理,目標威脅度得到更新。

想定在某一次任務的執行過程中,從不同方向和高度上,先后有多個低慢小目標出現。我方雷達和光電設備發現并對其中三個目標(目標A、目標B、目標C)進行偵測,并將目標信息上報至指控中心,指控中心依據獲取到的目標信息和當前系統所轄各設備信息,對目標的威脅程度進行分析。首先是目標A,在(T-1)時刻,假設指控中心通過偵測結果判斷目標A的距離在三級圈外；到了下一時刻T,指控中心判斷到目標A的類型為固定翼；(T+1)時刻,防控系統分析到我方可以有效處置目標A；其次是目標B,在(T-1)時刻指控中心通過偵測結果分析到目標B的距離在一級圈內；下一時刻T,指控中心獲取到目標的速度為9 m/s；(T+1)時刻,指控中心分析到目標B的類型為固定翼最后是目標C,在(T-1)時刻,指控中心通過偵測結果判斷到目標C的距離在二級圈內；T時刻,獲取到目標C的速度為2.5 m/s；(T+1)時刻,獲取到目標C的飛行高度為50 m。

利用動態貝葉斯網絡模型對上述目標態勢信息進行推理計算,同時建立靜態貝葉斯模型,也利用上述的態勢信息,對三個目標的威脅程度進行分析。基于動態貝葉斯網絡的目標威脅評估流程圖,如圖3所示。

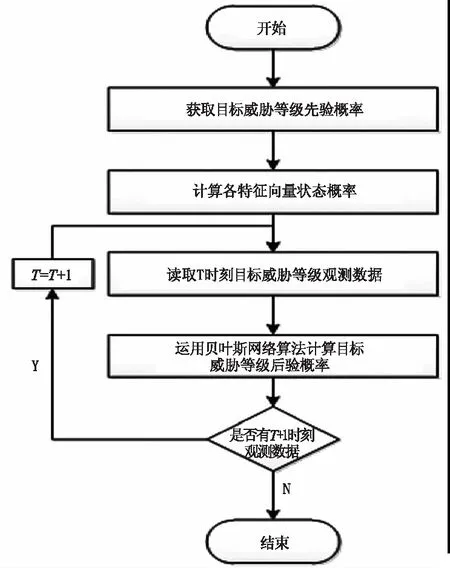
圖3 動態貝葉斯網絡威脅評估過程圖Fig.3 Threat assessment process of dynamic Bayesian network

基于靜態貝葉斯網絡的目標威脅概率分布,如表2所示。

表2 基于靜態貝葉斯網絡的目標威脅等級概率Tab.2 Threat probability deduced by SBN

在各個時刻利用動態貝葉斯網絡推理得到的威脅程度概率分布如表3所示。

表3 動態貝葉斯網絡推理的威脅程度概率Tab.3 Threat probability deduced by DBN

5 仿真結果分析

根據仿真結果可以看到,改變目標的先驗信息,可使評估系統計算得到不同的推理結果。

在靜態貝葉斯推理試驗的數據中,初始先驗信息為P(TL)=(0.251,0.312,0.437),目標各個威脅等級的概率分布比較平均,(T-1)時刻,系統對目標A的威脅等級計算結果為P(TL)=(0.229,0.294,0.477),T時刻評估結果為P(TL)=(0.172,0.313,0.515),(T+1)時刻的評估結果為P(TL)= (0.387,0.364,0.249)。在試驗過程中,模型在每一時刻的推理過程中并未利用上一時刻結果對先驗信息進行更新,每一時刻的推理過程都是相互獨立的,最終得到的目標的威脅等級的概率分布相差不大,而且概率最大的是威脅等級為高。

在動態貝葉斯推理試驗的數據中,在(T-1)時刻得到結果為P(TL)=(0.229,0.294,0.477),與基于靜態貝葉斯網絡進行目標威脅評估時,目標A的威脅等級在(T-1)時刻的結果相同；在時刻T,系統模型在進行推理時,將上一時刻的結果作為先驗信息,得到目標A的威脅等級為P(TL)= (0.042,0.261,0.697),目標威脅等級為中和高的概率降低,目標威脅等級為低的概率提升。在(T+1)時刻,利用T時刻的推理結果作為先驗信息進行推理,得到的評估結果為P(TL)=(0.071,0.348,0.581),雖然最終可以看到目標為低威脅等級目標,但是目標威脅等級中的高、中概率有了一定的提升。通過試驗可以看到,在最新時刻,模型進行目標威脅等級推理計算的結果明顯受到先前時刻目標威脅等級評估結果的影響,在整個試驗過程中,隨著試驗的進行,模型算法形成了信息積累的特點。

6 結 論

通過上述試驗可以看到,采用基于動態貝葉斯網絡的低慢小目標威脅評估算法進行試驗時,可利用上一時刻的計算結果進行學習并保存,而且隨著時間的推移,其得到的有效信息也越來越多,算法的精確性也穩步提升。因此可以認為,本文提出的一種低慢小目標威脅評估算法,可以有效地對目標威脅等級進行評估,且推算結果與專家系統評估接近,具有實用性。