基于聚類的煤礦井下鉆孔瞬變電磁異常響應邊界成像方法

范 濤，李 萍，張幼振，趙 睿，房 哲，樊依林，劉 磊，王 程，李宇騰

(1.中煤科工集團西安研究院有限公司，陜西 西安 710077；2.陜西省重點科技創新團隊(地球物理探測技術與裝備創新團隊)，陜西 西安 710077；3.煤炭行業工程研究中心(物探技術與裝備)，陜西 西安 710077)

近10 年煤礦事故總量逐年下降，但事故下降幅度趨緩。較大事故總起數、死亡人數總體呈下降趨勢，但從2013 年開始曲線斜率明顯趨平，2016 年后呈鋸齒形下降，2017 和2019 年等一些年份反彈，2020 年再度下降。重特大事故呈鋸齒形下降，同時波動幅度較大，2018 年后出現反彈，2020 年重特大事故總量與2019 年持平。事故中水害較大以上事故上升幅度大，2020 年發生較大以上水害事故3 起、死亡21 人，同比增加1 起、多死亡12 人，分別上升50%和133.3%，其中，較大水害事故2 起、死亡8 人，同比起數持平、少死亡1 人，重大事故1 起、死亡13 人，同比增加1 起、多死亡13 人，占全國煤礦較大以上事故起數和死亡人數的37.5%，經濟損失和社會影響非常嚴重[1]。而掘進工作面則是煤礦水害事故發生最多的地點[2]。因此，掘進工作面前方隱伏水害超前探測是亟待解決的技術難題。

水害隱患超前探查代表性的方法主要是瞬變電磁法、直流電法等電磁類方法[3-5]，但是，煤礦井下探測裝備功率受煤礦本安防爆限制，且井下環境的電磁干擾較大等因素的存在，致使礦井電磁類方法的探測距離短、精度偏低、多解性強[6-8]。為了解決煤礦井下掘進工作面前方的探測深度與探測精度的矛盾，許多學者逐步開始利用井下掘進工作面的鉆孔進行瞬變電磁探測工作，該方法可以在掘進前開展遠距離、高精度的隱伏水害超前預報[9-12]。

鉆孔瞬變電磁的數據處理一般采用電阻率反演成像方法，考慮到反演存在多解性，因此，反演擬合過程中為了提高精度，往往會選擇較為光滑的模型擬合實測數據，使得最終反演結果是一個電阻率連續光滑漸變的成像模型，在地質體邊界處的對比程度和變化情況較為模糊，很難清晰地反映地質異常體響應與背景值的差異，對異常體規模、形態的解釋工作常常需要經驗豐富的專家人為干預，也不利于生產中準確指導物探工作之后的鉆探和掘進工作。鑒于此，有必要研究一種提高成像結果中電阻率值聚合度，進而突出電性邊界的成像方法。

顯然，對電阻率的分區聚合屬于典型的分類問題，可以選用無監督機器學習方法進行解決。數據挖掘領域經常使用無監督機器學習算法，主要是采用它來發現大量無標簽數據的分布規律，實現對數據的區分或分類。經常使用的無監督機器學習方法主要有局部線性嵌入算法、主成分分析、局部切空間排列算法、拉普拉斯特征映射、等距映射和應用最多最廣的聚類算法[13]。

聚類算法是指基于一定的優化標準將一堆無標簽數據對象自動劃分成若干類別的方法，這個方法要求同一類別的數據具有相似的特征，不同類別的數據具有不同的特征[14]。

近年來，聚類方法已經廣泛被應用于地球物理領域的數據處理和特征挖掘中。尤其在地震勘探領域的應用較多，王偉濤等[15]通過層次聚類分析對汶川大地震的余震序列中的近似地震和重復地震進行了有效辨識；張巖等[16]采用結構聚類字典學習方法進行了地震數據隨機噪聲壓制方面的研究；S.Scitovski[17]采用基于密度的聚類方法對地震記錄進行了不同地震類型的劃分。在重磁資料的處理解釋中，張新兵等[18]基于改進的K-Means 聚類分析方法實現了重磁局部異常的自動圈定；李斐等[19]在優化不同區域的重力觀測密度方面應用了聚類分析方法；曹書錦等[20]開展了自適應模糊聚類對多異常源的精準確定工作。在電磁數據處理解釋領域，楊生等[21]在大地電磁曲線類型劃分中使用了聚類方法，對削弱地質推斷的多解性有較好的作用；SongYuchen 等[22]提出一種應用自適應密度聚類分類電測深曲線類型的方法；M.Audebert 等[23]結合了K-Means 聚類和電阻率CT 成像，提出一種多次反演解釋垃圾場滲流區的有效方法；李晉等[24]提出一種聯合聚類及遞歸的信噪比分離方法，對MT 低頻部分的數據質量有所改善。

本文參考以上資料，考慮不同的地質體存在電阻率差異，基于統計思想提出將具有相近電阻率值的成像元素劃分至一個類別，進而實現快速識別地質異常響應邊界的方法。本文討論了選用聚類方法的原則，介紹了聚類的方法原理，研究了確定最佳聚類條件的方法，最后使用三維數值模擬和井下實測數據檢驗了方法的有效性和實用性。

1 方法原理

1.1 聚類方法的選取

對電阻率進行聚類本質上是對一個一維數據體進行聚類，相當于對電阻率進行自適應層級劃分。絕大多數聚類算法都是針對二維及以上的數據，針對一維數據的聚類算法非常少，主要有K-Means 方法和Jenks Natural Breaks 方法。

K-Means 算法，也被稱為K-平均或K-均值算法，是一種廣泛使用的聚類算法。K-Means 算法以距離作為數據對象間相似性度量的標準，即數據對象間的距離越小，則它們的相似性越高，則它們越有可能在同一個類簇。之所以被稱為K-Means 是因為它可以發現K個不同的簇，且每個簇的中心采用簇中所含值的均值計算而成。

Jenks Natural Breaks 算法，也就是自然斷點分類，分類的原則就是將方差接近的放在一起，分成若干類。通過計算每類的方差和方差和，用方差和的大小來比較分類的好壞，值最小的就是最優的分類結果(但并不唯一)。

K-Means 和Jenks Natural Breaks 在處理一維數據時完全等價。它們的目標函數一樣，但是算法的步驟不完全相同。K-Means 是先設定好K個初始隨機點。而Jenks Natural Breaks 則是用遍歷的方法，一個點一個點地移動，直到達到最小值。顯然，n個數分成k類，Jenks Natural Breaks 就要從n-1 個數中找k-1 個組合。當數據量較大時，如果分類又多，計算量會顯著增加，因此，一般針對一維數組的聚類，更多選用計算量小的K-Means 算法。

1.2 K-Means 聚類算法

K-Means 算法的思想很簡單，對于給定的樣本集，按照樣本之間的距離大小，將樣本集劃分為K個簇。讓簇內的點盡量緊密地連在一起，而讓簇間的距離盡量大。

假設數據集為：

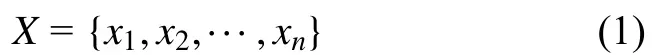
式中：n為數據個數；xi為除質心外的其他點。

劃分的簇為：

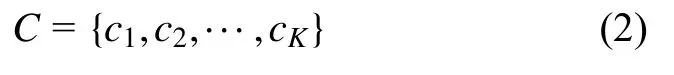
式中：K為預先設置的分類數。

此時，最小化平方誤差E即為：

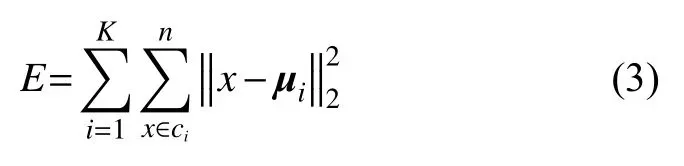
式中：μi是簇Ci的均值向量，也稱為質心，表達式為：

計算開始時，先采用隨機方式選定K個質心對所有數據進行初始分類，共分為K個初始類別，之后對所有數據計算它們與質心之間的歐氏距離，再依據這些距離的平均值更新質心和劃分類別，最后反復迭代該更新過程，直到滿足迭代的停止條件為止。

迭代的停止條件一般是質心變化率滿足下式：

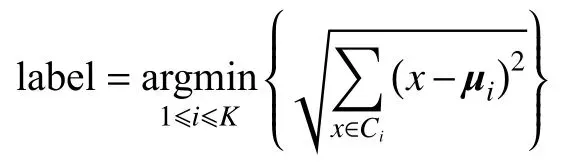
1.3 聚類中關鍵條件的確定方法

K-Means 聚類算法需要提前給出的條件主要有3 個：初始質心、聚類時的距離計算規則和聚類數目。

由于K-Means 聚類易陷入局部極小，不同的初始質心可能會導致不同的結果，本文根據聚類數目K的不同，選擇距離盡可能遠的K個點為初始質心，具體做法為：隨機選擇一個點作為第一個初始簇質心，然后選擇距離該點最遠的那個點作為第二個初始簇質心，然后再選擇距離前2 個點的最近距離最大的點作為第3 個初始簇的質心，以此類推，直至選出K個初始類質心。

考核類簇之間的相似性程度主要依靠各類簇之間的距離，較為常見的距離計算方法有歐氏距離、曼哈頓距離、夾角余弦距離和相關距離等。一般來說，歐氏距離最為簡單直觀，也更能反映數據在數值特征上的差別，因此，本文選擇使用歐氏距離。

聚類數目是K-Means 聚類算法中最重要的參數，因為不準確的聚類數目會明顯導致分類效果變差，但是目前并沒有依托數學原理的完美評價標準，本文采用基于組內平方誤差和(Sum of Squared Error，SSE)的肘部法則來確定最佳聚類數目。

組內平方誤差和(SSE)表示一個類簇內各點與該類質心的平方誤差之和，可由下式計算。

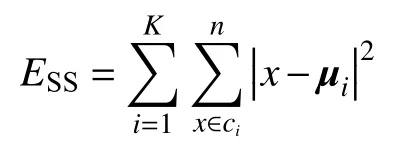
ESS越小則說明各個類簇越收斂，但顯然不是越小越好。因為考慮一種極端情況：將所有的樣本點均視作單獨類簇，此時ESS為0，而并未達到分類的目的。因此，需要在聚類數目和ESS之間尋找一個平衡點。

肘部法則就是這樣一種方法。指定一個j值，即可能的最大聚類數目。然后將聚類數目從1 開始一直遞增到j，計算出j個ESS。隨著聚類數目增多，每一個類簇中數據點數量越來越少，距離越來越近，因此，ESS值必然隨著聚類數目增多而減少。但當ESS減少得很緩慢時，可以認為進一步增大聚類數目分類效果也并不能增強，這個“肘點(拐點)”就是最佳聚類數目。

1.4 異常響應邊界成像步驟

應用K-Means 聚類方法實現對異常響應邊界成像的具體步驟如下：

(1) 對實測數據的Z分量數據進行視電阻率計算或反演成像，獲得(視)電阻率參數。

(2) 計算(視)電阻率參數不同聚類數目情況下的組內平方誤差和(ESS)，應用肘部法則尋找最佳聚類數目。

(3) 按照最佳聚類數目對(視)電阻率參數進行聚類。

(4) 將同一類中的(視)電阻率值全部更新為該類的質心值，并與原空間坐標重新對應。

(5) 對新的聚類后電性參數數據文件進行成像。

2 數值模擬效果

為驗證本文方法的成像效果，設計如圖1 所示的三維模型，采用時域有限差分方法進行了數值模擬。在鉆孔深度方向40 m 處，第一象限45°放置1 個規模為10 m×10 m×10 m 的低阻異常體，異常體中心點距離鉆孔15 m，采樣時間范圍為1×10-6～6.136×10-4s，模型其他參數見表1。

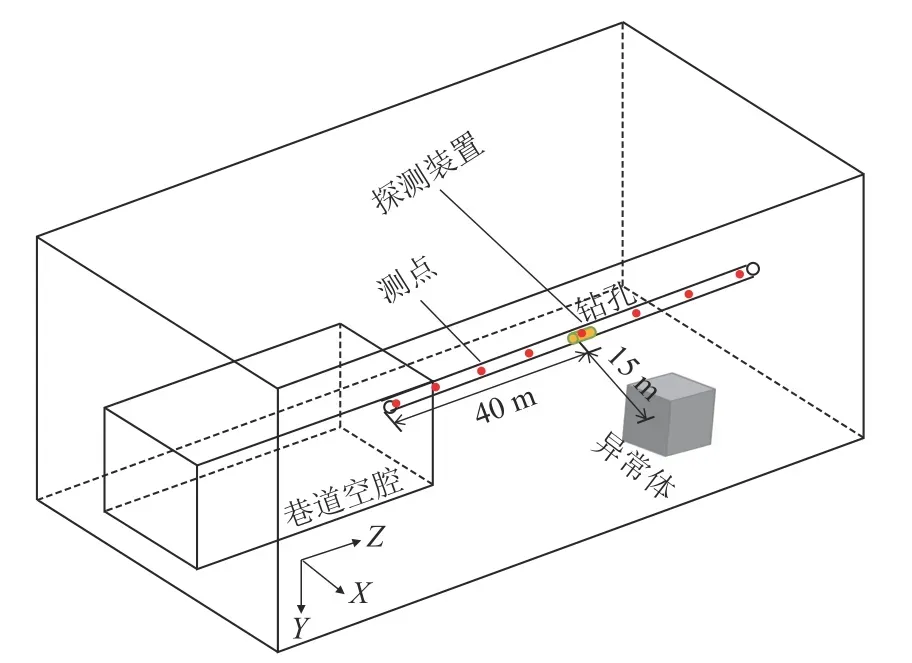
圖1 數值模型Fig.1 Schematic diagram of the numerical model

表1 模型參數Table 1 Model parameters

對26～54 m 范圍內的測點Z分量數據采用晚期視電阻率計算和層厚累加法進行視電阻率成像，可以得到如圖2 所示的沿鉆孔方向的視電阻率剖面圖，圖中橫坐標z為鉆孔深度，縱坐標r為徑向探測距離。可以較為清晰地看到在鉆孔深度40 m、鉆孔徑向15 m 位置有較為明顯的低阻異常響應(藍、綠色區域)。

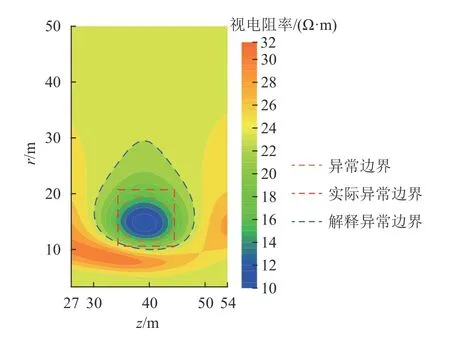
圖2 數值模型視電阻率剖面Fig.2 Resistivity profile of the numerical model

如果將藍色區域解釋為異常，則異常響應明顯小于實際異常體，二者面積比值約為0.624；如果將綠色區域解釋為異常，則異常響應明顯大于實際異常體，二者面積比值約為2.458；從圖2 中無法清晰反映異常響應的邊界，需要根據經驗人為解釋確定。

采用本文1.3 節肘部法則對模型視電阻率數據進行分析，可得到如圖3 所示的ESS曲線圖。由圖3 可知，在聚類數目為2 時曲線出現肘點，因此，選擇K=2，采用1.2 節中的K-Means 算法對模型視電阻率數據進行聚類處理，可得到圖4 所示的異常響應邊界成像結果。由圖4 可知，在鉆孔深度40 m、鉆孔徑向15 m 位置有明顯的孤立低阻異常響應(墨藍色區域)，異常響應邊界非常清晰，受晚期視電阻率計算和圖像插值算法的影響，異常響應形狀表現為直徑約10 m 的近似圓形，其與實際異常體(紅色虛線)的面積比約為0.985，整體參數與模型設置參數吻合較好。

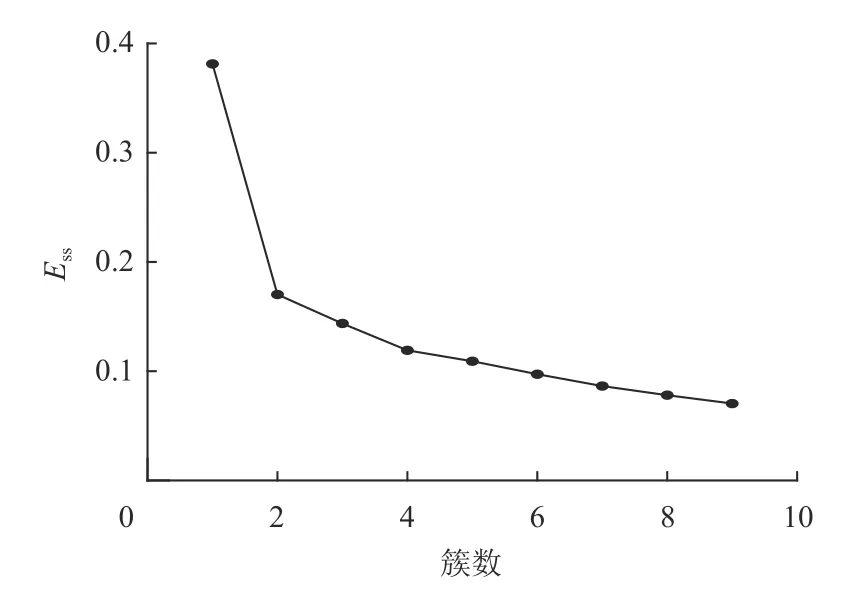
圖3 數值模型ESS 曲線Fig.3 ESS curve of the numerical model

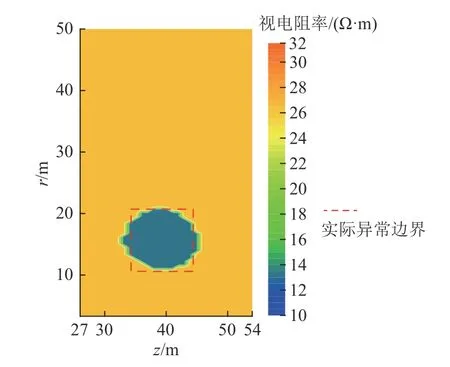
圖4 數值模型異常響應邊界成像結果Fig.4 Imaging result of anomaly response boundary of the numerical model

3 應用實例

為了驗證本文異常響應邊界成像方法對實際生產中煤礦積水采空區的實際解釋能力，在陜北某礦開展了鉆孔瞬變電磁探測試驗。該礦井屬于侏羅紀煤田，之前由于大量使用以掘代采的方式采煤，產生較多的小型采空區，且資料保留不完全，位置不明。礦區煤層上部有砂巖裂隙水，部分區段還有第四系松散層潛水，因此，這些采空區大部分為積水采空區，對該煤礦的安全生產造成了重要影響。

鉆孔瞬變電磁探測測點范圍為孔深60～128 m。對測點數據進行電阻率反演成像可以得到如圖5 所示的沿鉆孔方向的電阻率剖面圖。由圖5 可知，在鉆孔深度100 m、鉆孔徑向20 m 位置有較為明顯的低阻異常響應(藍、綠色區域)，與數值模擬結果類似，從該成果圖中無法清晰反映異常響應的邊界，需要根據經驗人為解釋確定。

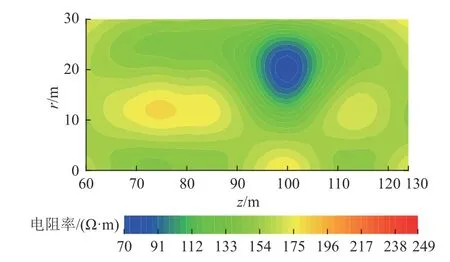
圖5 實測數據電阻率剖面Fig.5 Resistivity profile of measured data

同樣，采用本文1.3 節肘部法則對電阻率數據進行分析，可得到如圖6 所示的ESS曲線圖，由圖6 可知，在聚類數目為3 時曲線出現肘點，因此，選擇K=3。采用1.2 節中的K-Means 算法對電阻率數據進行聚類處理，可得到如圖7 所示的異常響應邊界成像結果。由圖7 可知，在鉆孔深度100 m、鉆孔徑向20 m 位置有明顯的孤立低阻異常響應(藍色區域)，異常響應邊界非常清晰，異常響應形狀表現為邊長約20 m 的三角形。礦方后期設計了上仰鉆孔對該異常進行勘查驗證，在進尺98 m 附近出現掉鉆和出水現象，最終推斷該異常為上組煤遺留的小煤窯采空區。

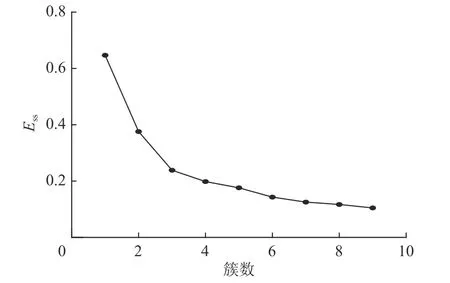
圖6 實測數據ESS 曲線Fig.6 ESS curve of the measured data

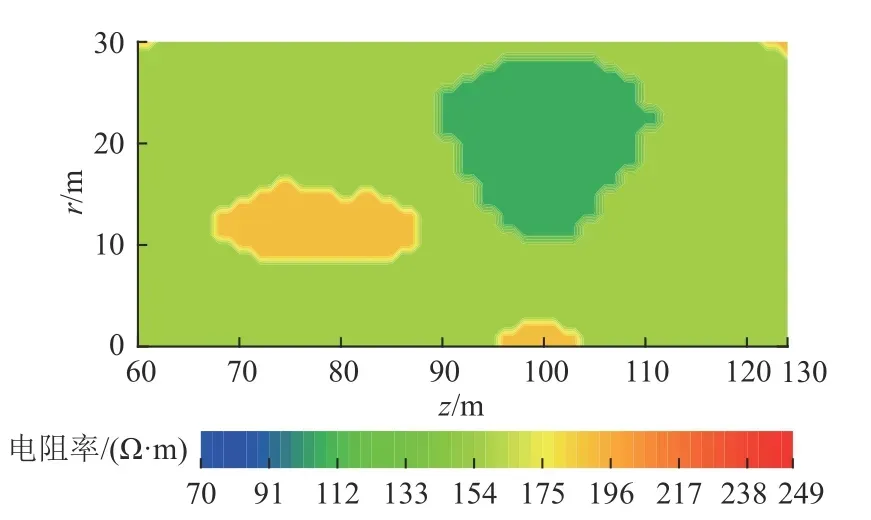
圖7 實測數據異常響應邊界成像結果Fig.7 Imaging result of anomaly response boundary of the measured data

驗證鉆孔開孔角度為上仰8°，此時鉆孔到達異常響應邊界的距離為96.89 m，與實際揭露采空區的距離相差1.11 m，誤差為1.13%。

4 結 論

a.鉆孔瞬變電磁反演結果一般為連續光滑漸變的電阻率成像模型，對背景值和異常地質體分界面的對比度表現得較為模糊，難以準確解釋異常響應的邊界。采用無監督機器學習中的聚類方法可以通過將相近電阻率值進行聚合分類實現異常響應邊界快速成像。

b.針對電阻率這一個特征值，從計算量考慮選擇K-Means 聚類算法，按照電阻率樣本之間的距離大小，對樣本進行分類。聚類計算中，基于最遠距離原則確定初始質心，距離計算方法選用歐氏距離方法，聚類數目應用基于組內平方誤差和(ESS)的肘部法則進行確定。

c.數值模擬數據的處理效果說明這種基于聚類的成像方法有效突出了異常響應邊界，清晰顯示了異常響應形狀；煤礦井下應用實例解釋的積水采空區經過實際鉆探驗證，說明了該方法在現實探查中的準確性和有效性，提高了巷道超前探測技術的精度和可靠度，為超前探測工程技術難題提供了重要的技術保障。

d.本文方法本質上是一種統計方法，并不僅僅適用于瞬變電磁法，也不僅僅適用于電阻率成像結果，對于以熱力圖形式表現的成像數據，如音頻電透視及無線電波透視成像結果、直流電法探測成果，也均可應用。