復雜配水系統的最優抽水調度

馮劉成

(新疆維吾爾自治區塔里木河流域干流管理局，新疆 阿拉爾 843300)

近年來能源價格上漲使得能源成本在灌溉供水系統(WDS)總成本中占據了相當大的比例[1]。因此，建立節能型WDS對于保證灌區的可持續發展非常重要，同時也能降低大量成本[2]。在電價結構的基礎上采取最優的抽水方案是降低能源成本的有效措施。在現代灌溉WDS中，通常修建有一些水庫，可以在低電價時將水提到水庫中，從而達到降低經濟成本的目的。向水庫中抽水的另一個優點是使泵的運行更加穩定，能在一定程度上延長抽水系統的工作壽命[3]。

最優調度問題通常都比較復雜，取決于許多變量，如電價結構、抽水能力、供水系統能力、可用蓄水量和灌溉需求模式。近年來，系統方法已被廣泛應用于解決該問題，包括單目標、多目標遺傳算法和蟻群優化算法等等[4-5]。系統方法適合于多峰復雜問題，然而，當處理例如供水管網系統這樣具有大空間的復雜系統時，由于需要對大量的場景進行評估，搜索最優值需要很長的計算時間，同時這些方法也不能保證提供最優結果，而是一個相對接近最優解的近似解。相比之下，線性規劃(LP)能確保取得最優解，并且它們運行更快、更穩定、更高效，適合解決實時控制問題。本研究開發了一種抽水計劃優化調度模型，目的是最小化系統的能源成本。管理者可以使用該模型作為決策工具，為系統選擇最優的抽水方案。

1 方法

1.1 模型

該模型的目標是在給定的電價條件下，給出能源成本最小的最優抽水計劃。采用線性規劃算法，優化變量是價格周期k(vj,k)內每個抽水系統j的抽水量。通過抽水系統在每個時段的抽水量及其抽水時間計算抽水能力。

總能源成本(C)的計算方法是用每個周期的能源價格(Pk)乘以每個泵在周期內消耗的能量(Ej,k)，如公式(1)所示：

C=∑?j∑?kPk·Ej,k

(1)

式中：C為總能源成本，元；Pk為每個周期的能源價格，元/kJ；Ej,k為每個泵在周期內消耗的能量，kJ。

在周期k消耗的能量是泵功率和工作時長的函數，即抽水量vj,k。可用公式(2)表示：

(2)

式中：γ為電機的安全余量，取1.2；Hj為水泵揚程，m；η為水泵的效率；Vj,k為周期抽水量，m3。

每個周期和抽水系統的抽水量不能超過該系統的最大抽水量，將泵送能力表示為系統流量Qj和周期Nk的函數，如公式(3)：

Vj,k≤Qj·Nk

(3)

式中：Qj為系統流量，m3/s，Nk為周期，s。

引入了最大和最小存水容量限制，防止蓄水池中的水量超過其最大容量，從而導致溢流或超過安全限制水位。

第k個周期結束時儲存水量Sk的計算方法是抽水至水庫的累積水量與累積用水量之間的差額，再加上初期儲存的水量So，如公式(4)所示，dk是第k個時段的需水量。

Sk=So+∑k(∑jVj,k-Dk)

(4)

式中：Sk為k個周期結束時儲存水量，m3；So為初期儲存的水量，m3；Dk為第k個時段的需水量，m3。

最大和最小蓄水容量(分別為SM和Sm)的限制如下：

Sm≤Sk=So+∑?k(∑?jVj,k-Dk)≤SM

(5)

式中：SM為周期最大儲存水量，m3；Sm為周期最小儲存水量，m3。

對總抽水量施加限制，從而控制水庫的最終蓄水位(SF)。如果不施加這一限制，方案會在最后一段時間清空水庫。這一限制可用公式(6)表示：

∑?k∑?jVj,k-Dk=SF-So

(6)

式中：SF為控制水庫的最終蓄水量，m3。

1.2 軟件程序

本研究開發了一套軟件程序，用于求解最優抽水計劃。該軟件有一個優化模塊，通過修正的單純形算法解決線性規劃問題。該模型需要建立關于電價、需水量和抽水系統的輸入數據庫。當選擇了特定的電價時，程序會從數據庫中讀取有關該電價的信息，由一個子程序通過特定電價生成價格向量，其維度等于研究時間范圍內的價格周期，該價格向量用于計算目標函數。另一個子程序從用水需求數據庫中讀取日用水量和日需求模式，并計算每個時段的需水量。利用該信息，程序計算包含目標函數系數的向量、包含約束系數的矩陣、包含約束的向量，信息被傳遞給優化子程序，并且將模型的運行結果導出在電子表格中，以供后續的處理。

2 案例研究

本文以新疆某灌區供水管網系統為例，該管網是一個加壓的按需管網，總管長123 km。三座調節性水庫位于同一高程，總庫容25萬m3，水通過重力作用分配到灌區各部位。灌區水源是從地下含水層中抽取的水。灌區有15口水井，分成三個區域。這些井的動態水位超過100 m，開采深井水需要很大的能源成本從這三組井中抽出的水通過管道輸送到一個泵站。來自這3個抽水站的水被注入抽水渠，并流入調節水庫。將水從抽水站提升至調節水庫需要額外的能源成本。圖1給出了WDS網絡布局及方案。

圖1 WDS網絡布局及方案

通過管理每組井的開始和停止時間來控制系統的運行。每組中的井泵通常同時運行，將抽出的水倒入每個泵站的小蓄水池。當所有的井泵一起工作時，它們在半小時內裝滿。當蓄水池裝滿后，泵站中的水泵開始運轉。在該系統中，井下泵連續運行，管理人員控制其啟動和停止時間，而泵站間歇運行，其功能由最小-最大水位控制自動控制。

抽水方案是在低能源價格時段進行抽水，特別是在該地區農作物用水需求較低的時候。在晚上和周末一般能源價格較低，而灌溉主要在早晨進行，因此抽水和用水幾乎不會同時發生。

2.1 抽水系統建模

該灌區的抽水系統由15個潛水泵和3個增壓站組成，潛水泵將水從井提升到吸水箱，3個增壓站將水注入WDS。為了降低其復雜性和便于建模，通過合理的假設，提出了一種簡化的抽水模型。

2.1.1 井的簡化方案

每組井中的潛水泵總是同時運行，向三個增壓站抽水。流量和泵送之間略有不同，將每套井簡化為由一個等效泵組成的簡化系統。該等效系統的流量Qsd和功率Pss是由每臺泵的流量和功率相加得到的。對于此等效系統，滿足以下關系式(7)：

(7)

式中：Hs、Hi為系統和每個泵的平均壓能；ηs、ηi分別為系統的平均效率和每個泵的效率；γ為水的容重。

考慮到井泵在固定的工作點工作，并且它們的特性彼此相似，故假設井泵的效率也是相似的，等效系統的平均揚程可以通過式(8)計算：

(8)

式中：Hs為等效系統的水泵揚程，m；Qi為系統的每個水泵的流量，m3。

表1給出了關于每口井的流量、揚程和功率的數據。

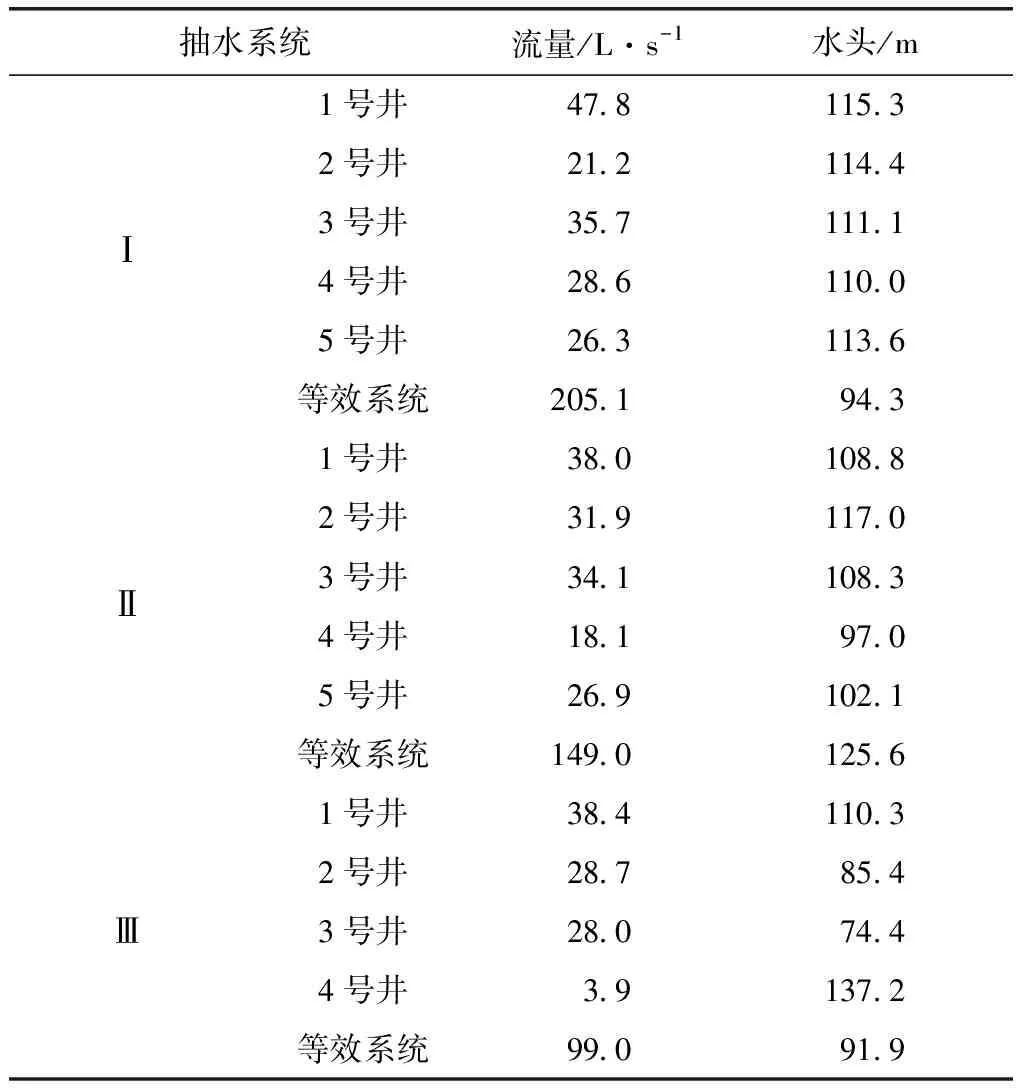
表1 三個井組的等效系統

2.1.2 增壓站的簡化方案

三個增壓站的運行是間歇性的，由蓄水池中的最大-最小水位傳感器自動控制。然而，在一段足夠長的時間內，蓄水池中的儲水總量變化是可以忽略不計的，這些站抽出的平均水量等于每組井供應流量的總和。

抽水和需求的時間不一致說明大部分的水都需要經過調節水庫；網絡規模過大，系統內部的水頭損失相對較小。由于上述原因，測壓水頭是恒定的，主要取決于調節水庫和吸力之間的高差。為了闡述這一過程，圖2給出了特定月份(2018年7月)的壓力變化情況和增壓站I整個周期內的壓力直方圖。

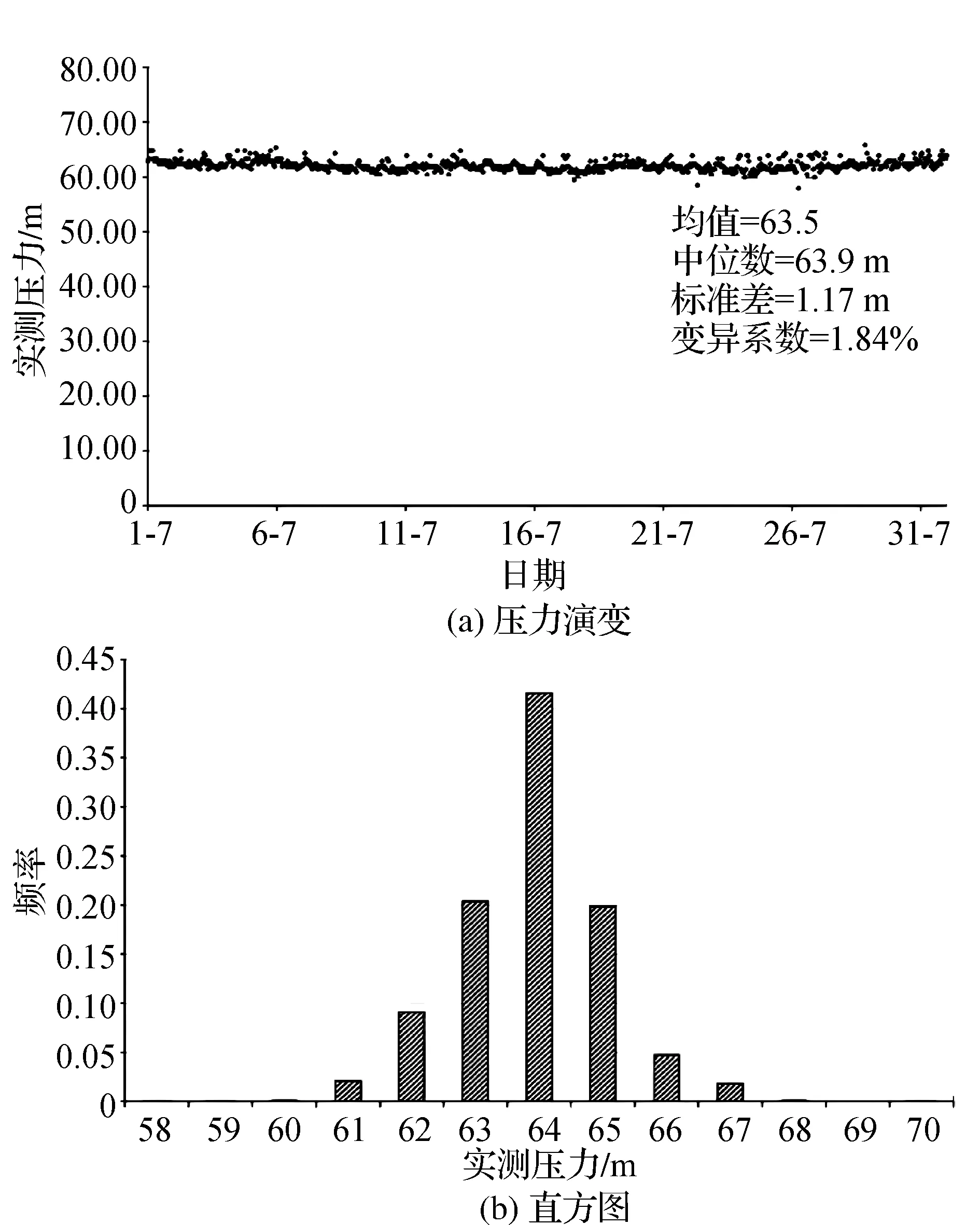
圖2 增壓站I

測壓站的平均測壓水頭是根據測得的壓力和蓄水池平均水位計算出來的。表2給了計算結果。

表2 三個增壓站的測壓壓頭

在計算和測量的基礎上，將各井組及其配套的增壓站聯合運行模擬為兩個串聯的抽水系統。在兩個泵串聯的情況下，流量相同，系統的揚程和總功率分別等于兩個泵的揚程和功率之和。使用每個抽水系統的能耗數據，通過公式(9)計算每個等效系統的整體抽水效率值。

(9)

式中：Hg為整個系統(井和增壓站)的泵頭，m；Qg為系統的流量，m3/s；Eg為整個系統的年能耗，kJ。

表3 等效泵送系統的特性

2.2 用水量分析

該網絡的遠程控制系統將每日消耗量傳輸并存儲在數據庫中。通過該數據庫可以獲得整個灌區的日用水量情況。如圖3所示。

圖3 灌區的日用水量

如圖4所示，用水需求集中在兩個高峰期。用水主要在早上和晚上。21點后的用水量微不足道，可以忽略。

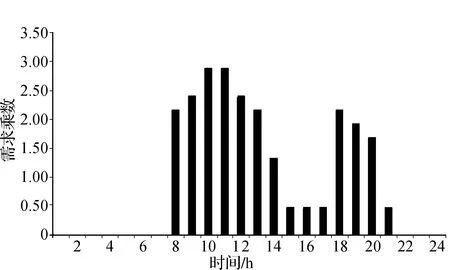
圖4 日需水量模式

3 討論

3.1 三套抽水系統同時運行

使用此方案執行了三次模型運行。每次運行都會針對不同的替代電價計算最佳抽水計劃。期初假定調節水庫半滿(125 000 m3)，期末假定蓄水量保持不變，以確保全年抽水量等于年用水量。對三種替代電價進行了比較，并計算了總能源成本。由此得出3.0 A，3.1 A和6.1 A下的最優成本分別為3 643 661元、3 417 191元和2 768 606元。可以看出在6.1A的電價下，能源成本最低。將灌區實際能源成本(3 430 800元)與模型得出的最優成本進行比較，發現優化后的方案可以顯著節省成本。

圖5給出三種情況的蓄水量變化。所獲得的最低總能源價格是通過在需求高峰期充分地利用水庫中儲存的水量，在能源成本較高的時期減少抽水達到的。

圖5 3.0A、3.1A和6.1A下的最優水庫蓄水量

3.2 三套抽水系統的獨立運行

為了評估是否有潛在的成本節約，三個抽水系統分別獨立運行。本次運行使用了之前最好的6.1 A情景。

結果表明，三個系統獨立運行比同時運行更節能，可以節省3.7%的能源成本(同時運行成本為2 768 606元，單獨運行成本為2 665 418元)。因為當泵送系統獨立工作時，該模型優先考慮效率更高的系統。圖6顯示了泵系統在獨立運行期間的最佳運行時段。在這種情況下，系統Ⅰ的運行時間占總運行時間的50.0%以上。系統Ⅱ為41.0%，而系統Ⅲ只有6.7%。系統Ⅲ運行時間短的原因是其效率低。應通過設計渠道提高其效率，以獲得較高的整體系統效率，并使三個抽水系統的運行時間更加均勻。圖6給出了獨立運行和同時運行下調節水庫全年蓄水量的變化。

圖6 同時運行和獨立運行的水庫蓄水位變化

將最優抽水方案與系統的實際運行方案進行比較，模型得出的最優能源成本(2 665 418元)低于實際成本(3 430 800元)，節約了23.9%。

4 結 論

本文通過線性規劃建立了最優抽水調度模型，并將其應用于新疆某灌區，該模型提供了最優的抽水計劃，并且將總能源成本最小化。該模型還可以比較不同的替代電價，以提供最佳方案。將最優抽水方案與系統的實際運行方案進行比較，模型得出的最優能源成本(2 665 418元)低于實際成本(3 430 800元)，節約了23.9%。證明該模型是一個有效的決策工具，可以幫助系統管理人員選擇和實施適合系統的運行模式。