非圓齒輪系齒廓曲線的優化設計計算方法研究

張秋菊，孫智甲，楊晰予，王柯翔

（河南理工大學，河南 焦作 454003）

0 引 言

非圓齒輪系液壓馬達是一種新興的、綜合性能優異的液壓馬達，能夠被廣泛應用在煤礦、建筑、船舶、航空航天等行業，具有很好的應用前景和較高的市場價值。非圓齒輪行星輪系是非圓齒輪液壓馬達的核心運動機構。在非圓齒輪系中，非圓齒輪的節曲線多采用高階橢圓曲線，類型變化多樣，沿節曲線均布的齒廓曲線每條都有不同的長度和形狀，這些特點給馬達虛擬樣機的建立以及數控加工模型的建立帶來了不小的困難。設計符合齒輪系運動關系的沿非圓形的節曲線均布的齒廓曲線，不僅是進行非圓齒輪系傳動設計的核心內容，同時也是進行非圓齒輪系的運動學、動力學相關理論研究的基礎。因此，開發一種能夠快速生成非圓齒輪系齒廓曲線的數值算法是目前亟待解決的關鍵問題。

共軛嚙合算法由于計算邏輯清晰，目前被廣泛用于非圓齒輪系的齒廓坐標的計算。根據非圓齒輪系的嚙合運動原理，共軛嚙合法計算行星輪在任意運動時刻與非圓齒輪的嚙合點的坐標，并利用多次坐標變換最終計算非圓齒輪的齒廓坐標。在理論上，計算獲得的齒廓坐標的數量越多，由齒廓坐標所擬合的齒廓曲線就越精確。盡管現有的算法通過增加齒廓點的坐標計算，能夠提高對齒廓曲線的設計計算精度，但這樣會帶來更多的數值計算量，進而提高設計計算的計算機硬件成本，尤其會降低設計計算的效率。

為了提高對非圓齒輪系的齒廓曲線的設計計算效率，基于共軛嚙合算法，本文利用預存數據插值法代替目前算法中大量的對于內齒圈極角的微分方程的求解計算，進而提出一種針對非圓齒輪系的齒廓曲線設計的優化算法。本文利用非圓齒輪系的仿真傳動試驗，在理論設計層面對算法進行了驗證；利用非圓齒輪的金屬線切割加工和實際的齒輪傳動試驗，驗證了算法的工程應用價值。

1 非圓齒輪的齒廓點坐標的數學計算模型

在非圓齒輪系的運動中，如果不考慮齒輪嚙合所發生的滑移，則非圓齒輪的齒廓點是它們與行星輪齒廓曲線的瞬時重合點，即瞬時的嚙合點。因此，本文建立如圖1所示的數學模型，該模型利用坐標變換的方法計算非圓齒輪的齒廓嚙合點的坐標，進而擬合出非圓齒輪的齒廓曲線。

圖1 非圓齒輪齒廓點坐標的數學計算模型示意圖

在內齒圈、行星輪、太陽輪的幾何中心分別建立隨之運動的極坐標系XOY、XOY、XOY，其中O和O重合。假設圖1（a）所示的為齒輪系運動的初始時刻，在此刻，三個極坐標系的Y 軸的正方向重合。當太陽輪繞O點沿順時針方向旋轉，在齒輪傳動的下一個任意時刻，如圖1（b）所示，行星輪的節圓與內齒圈、太陽輪的節曲線分別相切于圖示C 點和D 點，由三心定理證明，C、D 與O在一條直線上。圖中C 點在內齒圈的隨動坐標系XOY中所對應的極角為，D 點在太陽輪的隨動坐標系XOY中所對應的極角為。

1.1 數學模型的基本方程

依據非圓齒輪系的運動學規律，在齒輪系的嚙合運動中，內齒圈、太陽輪做同軸的自轉運動，行星輪自轉的同時繞太陽輪公轉，并且行星輪的節圓與內齒圈和太陽輪的節曲線做相切的純滾動，由此，太陽輪的節曲線是內齒圈的節曲線的共軛曲線。在坐標系XOY中，如果給定內齒圈的節曲線方程為：

其中，是的函數，其具體形式由設計確定。

由共軛嚙合算法可以推導出太陽輪的參數方程：

1.2 非圓齒輪齒廓坐標點的數學計算

以行星輪的中心為原點，建立直角坐標系XOY和XOY，要求兩個坐標系的Y 軸的正向分別為從O點指向C、D 的方向。如圖2（a）所示，Y與Y的夾角為，Y與Y的夾角為。此刻，如果行星輪齒廓上一點S 與太陽輪齒廓嚙合，假設它們的齒廓為理想曲線，那么S 點同樣是太陽輪齒廓上的一點。

圖2 齒廓點的坐標變換示意圖

根據齒輪系中各齒輪的節曲線純滾動的假設，Y與Y的夾角可以用下式計算：

與對應的是Y與Y的夾角，用下式計算：

在行星輪的傳動過程中，()和()具有唯一的對應關系。

對于使用漸開線齒廓設計的行星輪，如圖2（b）所示，在坐標系XOY中，S 點的坐標為：

其中，||和可以聯立下列方程計算：

上述方程中，r是行星輪節圓半徑，是行星輪的齒數，是分度圓壓力角，是行星輪在Y和Y的負半軸之間的輪齒數。

利用坐標系XOY和XOY之間的坐標變換，最終能夠計算出S 點在太陽輪隨動坐標XOY中的坐標，即計算出來太陽輪齒廓上一點的坐標：

其中，（，）是行星輪中心在坐標系XOY中的坐標。

采用上述的計算方法，利用XOY與XOY之間的坐標變換，同樣能夠計算獲得C點所對應的內齒圈齒廓點的坐標。

2 非圓齒輪齒廓點坐標的數值優化算法

非圓齒輪與行星輪的齒數比確定之后，需要計算的齒廓數量，即式（6）中的值的范圍是確定的。從圖2（b）可以看出，在齒輪的嚙合過程中是單調變化的。

當值確定，即當行星輪的第個輪齒與太陽輪嚙合，在該輪齒脫離嚙合之前，∈(，)，其中對應于行星輪齒根嚙合，對應于行星輪齒頂嚙合。設數組：

其中，=t，=t，=+（t-t）/(-1)，≤。值設定越大，對齒廓點的計算數量越大，對齒廓曲線的擬合精度相對越高。

當設定了，容易根據()和()的對應關系計算()對應的數組。此時，現有的計算方法會將帶入式（4），利用微分方程求解=[，，…，]。在獲得數組之后，聯立方程（5）（6）和（7）最終獲得各齒廓點的坐標(，)。在每個齒廓點坐標的計算中，上述方法都要將帶入式（4），求解一次復雜的微分方程。高精度的齒廓設計計算需要大量的齒廓點坐標，因此，上述方法會帶來大量的數值計算量。為了減少數據計算量，提高對非圓齒輪的齒廓的設計計算效率，本文提出預存數據插值法解決上述問題。

本文首先建立數組=[，，…，]，利用方程（3）和（4）獲取預存數據=[，，…，] 和=[，，…，]，則通過一次計算獲得了內齒圈節曲線的極角與行星輪嚙合轉角以及的關系。在后續的計算中，可以根據設計需要確定和的值，然后利用對預存數據的插值快速計算出它們所對應的值。本文所提方法的具體步驟，參加圖3所示的計算流程。

圖3 齒廓點坐標的數值計算流程圖

3 算法的試驗驗證與分析

3.1 行星輪齒廓與非圓齒輪齒廓的干涉驗證

基于本文所提算法，以為驅動變量，編寫內齒圈和太陽輪齒廓曲線的設計計算程序，并將每個計算位置的行星輪齒廓曲線與非圓齒輪齒廓的擬合曲線輸出在非圓齒輪的隨動坐標系中，如圖4所示。

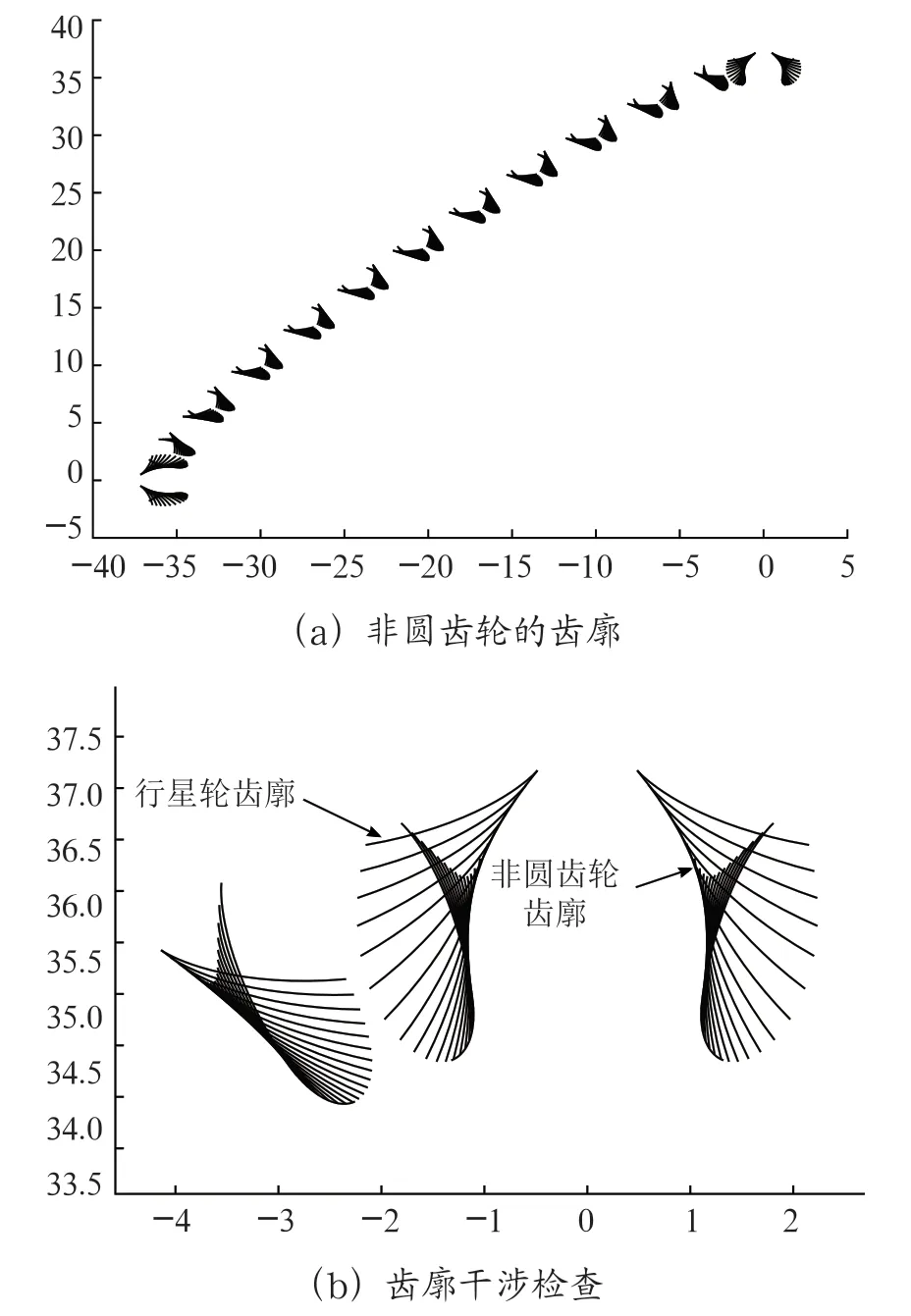
圖4 利用計算程序生成的非圓齒輪的齒廓曲線

從圖4可以看出，行星輪的齒廓在每個位置都與擬合所得非圓齒輪的齒廓曲線相切，并且沒有發生齒廓的干涉問題，由此可以證明，本文所提算法能夠正確計算非圓齒輪的齒廓點的坐標，所擬合的齒廓曲線在理論上能夠實現非圓齒輪系的運動學原理，且不會發生輪齒干涉問題。

3.2 非圓齒輪系的傳動試驗

3.2.1 數值傳動仿真試驗

利用圖4中所示的可視化界面對非圓齒輪系進行了靜態干涉檢查之后，還需要建立齒輪系的傳動仿真模型，進而驗證算法生成的齒廓在運行中是否發生“卡齒”問題。

將算法生成的齒廓導入CAD 軟件，建立非圓齒輪系的三維數字模型，然后使用Adams 軟件建立起齒輪機構的傳動仿真模型。在仿真模型中，內齒圈被施加固定約束，太陽輪被施加與內齒圈軸線重合的旋轉約束，行星輪被施加了與非圓齒輪的接觸約束。在對非圓齒輪機構的傳動仿真的過程中，太陽輪被施加勻速的定軸旋轉動力，太陽輪在定軸旋轉的同時，通過齒面接觸力推動行星輪運動，從而模擬行星輪機構的實際的嚙合運動。圖5（a）所示為行星輪的仿真運動軌跡。

除了對齒輪機構的嚙合運動進行可視化的仿真之外，傳動仿真模型還實時采集齒輪機構的運動學和動力學的仿真實驗數據，并將行星輪的仿真軌跡與理論軌跡進行對比，如圖5（b）所示。上述的傳動仿真試驗的結果表明，使用本文算法所設計的非圓齒輪系傳動結構，在運動中能夠實現行星輪的預設傳動軌跡，實現預期的嚙合傳動。本文利用非圓齒輪系的傳動仿真模不僅驗證了所提出的齒廓算法，而且獲得了齒側隙的設計范圍。研究發現如果行星輪與非圓齒輪的齒側隙如果超出了該設計范圍，無論是側隙過大，還是側隙過小，非圓齒輪機構在傳動過程中都會發生“卡齒”的問題。

圖5 非圓齒輪結構的傳動仿真模型和傳動仿真數據

3.2.2 非圓齒輪系的加工和傳動試驗

參照仿真試驗所確定的齒側隙的設計范圍，使用本文算法生成非圓齒輪的齒廓數據，將其導入金屬線切割設備中，實際加工了液壓馬達的非圓齒輪傳動機構，圖6（a）所示。

圖6 非圓齒輪的加工和傳動試驗

設計并加工專門的非圓齒輪系傳動試驗裝置，使用齒輪傳動試驗臺，進行了非圓齒輪系的傳動試驗，如圖6（b）所示。試驗結果表明，所加工的非圓齒輪系的傳動機構，在太陽輪的轉速低于800 r/min 的條件下，未出現齒輪卡死，未產生劇烈的機械振動。綜上結果表明，本文所提的算法能夠被用于非圓齒輪系的工程設計中，具有較好的工程應用價值。

圖6 HMI 顯示界面

4 結 論

（1）基于非圓齒輪系的共軛嚙合算法，本文提出了一種非圓齒輪系齒廓曲線的優化設計算法，該算法利用對預存數據的插值算法，減少傳統算法中大量的微分方程的求解計算，從而優化了算法的計算效率。

（2）本文建立了非圓齒輪系的傳動仿真模型，通過傳動仿真試驗對算法生成的齒廓曲線進行了傳動仿真驗證。仿真結果表明，使用本文算法所生成的齒廓曲線能夠實現行星輪的預設傳動軌跡，不會發生“卡齒”問題。

（3）利用算法生成的齒廓數據，本文加工了非圓齒輪，并利用所加工的齒輪完成了非圓齒輪系的齒輪傳動試驗。試驗結果表明，本文算法所設計的齒輪能夠直接用于工程實際。

綜上所述，本文提出了一種用于非圓齒輪系齒廓曲線設計的優化數值算法，該算法對于非圓齒輪系的優化設計理論的發展，以及工程應用的推廣具有一定的價值。