“康熙十四管律”的律學分析

○ 白怡寧

“康熙十四律”是一個持續較久的研究議題，迄今沒有特別清晰的結論。這部分內容主要在《御制律呂正義》（后文簡稱為《律呂正義》）的上編兩卷①筆者使用的版本是《御制律呂正義》上編卷一、卷二，載《景印文淵閣四庫全書》（第215冊），臺北：臺灣商務印書館，1986年。后文腳注中不再一一注明。中。筆者經過深讀原文和已有的解讀觀點，得出一些心得，認為十四律內部并不是完整的相生關系。

《律呂正義》認為三分損益法和隔八相生法所述內容不同，②《審定十二律五聲二變》，《御制律呂正義》上編卷一，第17頁。“言樂者皆知三分損益、隔八相生，然此二者義各有在，不可一概而論。三分損益乃制律之則也，古圣人立為算術以別十二律呂相生之度……隔八相生乃審音之法也。審音之法，必取首音與第八音，葉和同聲，以為之準。即首音八音之間，區而別之，以為五聲二變，則清濁之相應，高下之相宣，皆賴以生焉。”三分損益法視作生十二律的準則，無論什么樂器均按照此規則來定律；而隔八相生法是對高低八度音的校音審定。這里的“審音之法”是指七聲音階包含五聲二變，第八音則通過“葉和同聲”并區別清濁。而歷代文獻對“隔八相生”則解釋為“陰陽相生，自黃鐘始而左旋，八八為伍”③《漢書·卷二十一·律歷志》，北京：中華書局，1962年，第965頁。。《中國聲學史》現代解釋則是：“如果按音高順序將十二律排成行或圈，按照下生（三分損一），每生一次，其律位向音高方向（或向短律方向，又稱左旋）移動八個位置（包括起始律與終止律）。”④戴念祖：《中國聲學史》，石家莊：河北教育出版社，1994年，第174頁。所以《律呂正義》對“隔八相生”的認識與古來所論并不相同。

《律呂正義》還規定了弦、管兩種不同振動體在八度相應方面的長度比差異。原文如是：

間嘗截竹為管，詳審其音，黃鐘之半律不與黃鐘合，而合黃鐘者，為太簇之半律，則倍半相應之說，在弦音而非管音也明矣。⑤《審定十二律呂五聲二變》，《御制律呂正義》上編卷一，第18頁。

大凡弦度無論長短，其全半聲必相應。管律同徑者亦無論長短，但取其九分之四則聲相應。⑥《明管音弦音全半聲之不同》，《御制律呂正義》上編卷二，第45頁。

這兩段說得非常清楚，即弦的全半長度必為八度關系，即2∶1，以黃鐘為例，全弦為黃鐘，半弦則為半黃鐘。但從實驗來看同徑管基音與高八度音之間的長度比關系并不是2∶1而是9∶4。

“隔八相生、葉和同聲”與“管律八度9∶4”這兩點對于理解《律呂正義》十四律具有關鍵性意義。

一、《律呂正義》對“康熙十四律”的描述

《律呂正義》不認同歷史上雅樂七聲音階形態，因為律呂排列“陰陽相雜”⑦同注⑤，“而旋宮之義已失，且陽律而雜以陰呂，陰呂而雜以陽律，陰陽相雜。而取聲之原，亦未為得是。”。所以十四律重點為陽律陰呂不能相雜，黃鐘均均主是陽律，黃鐘均“五聲二變”加第八音也必為陽律，大呂均各音皆為陰呂。原文如下：

故今所定，黃鐘為首音宮聲。次太簇為二音，以商聲應。姑洗為三音，以角聲應。蕤賓為四音，以變徵聲應。夷則為五音，以徵聲應。無射為六音，以羽聲應。半黃鐘為七音，以變宮聲應。此陽律之五聲二變也。至半太簇為清宮，而與黃鐘應，則陽律旋宮之義見焉。

如定大呂為首音宮聲，則夾鐘為二音，以商聲應。仲呂為三音，以角聲應。林鐘為四音，以變徵聲應。南呂為五音，以徵聲應。應鐘為六音，以羽聲應。半大呂為七音，以變宮聲應。此陰呂之五聲二變也，至半夾鐘為清宮，而與大呂應，則陰呂旋宮之義見焉。所謂陰陽以類相從而不雜者此也。⑧同注⑤。

根據上文制成“五聲二變”兩均結構表：

從這個表格反觀前文提及的兩點，我們找到了十四律的內在理路：1.維持一均七聲加高八度音的陰陽同屬需十二律加兩律，最后兩律同陽或同陰；2.高八度音與弦律大全音高八音同，故9∶4由來于此，并非計算而得的管律數據。由此，可以對“康熙十四律”作出進一步的定義性說明，即此“十四律”是在三分損益相生十二律的基礎上，最后兩律并非連續生律而得，只是按照陰陽同類的八度添加，以黃鐘均為例，加半黃鐘、半太簇兩律，其他各均依此類推。所以這不是一種律制，而是解決“五聲二變加第八音”并“陰陽以類不雜”的權宜之為。

表1展示出兩均結構平行以及陰陽各屬其類。這個格局似乎可以與雌雄笛的實踐相聯系，比如昆曲伴奏樂器“雌笛小工調，生旦用；雄笛筒稍粗，低半音，用于老生花臉，二者吹奏技法同”⑨《中國戲曲音樂集成》編輯委員會、《中國戲曲音樂集成·江蘇卷》編輯委員會：《中國戲曲音樂集成·江蘇卷》，北京：中國ISBN中心出版社，1992年，第57頁。。黃鐘均和大呂均結構從階名表述完全一致，七聲具備。但這形成了所謂全音階樣式，與七聲音階的音樂實踐不符。

表1 “五聲二變”兩均結構表

《律呂正義》在表述“康熙十四管律”的內容時始終保持“陰陽以類相從而不雜”，各均皆需在十二律基礎上增加陰陽同屬兩律而成十四律。上編卷二《旋宮起調》篇是關于律管簫笛旋宮轉調的論述，目的在上承中古一均四調七均二十八調的傳統，十四均可得五十六調，下接當世樂工度曲七調相轉之法。原文詳細制作了管樂器十四均的旋宮圖譜，皆為從下羽開始含第八音的陰陽同屬音列結構。僅舉管樂器旋宮圖譜前兩均⑩《旋宮起調》，《御制律呂正義》上編卷二，第66–67頁。“黃鐘宮聲立宮，倍夷則下羽主調，為上字調”和“大呂清宮立宮，倍南呂清下羽主調，為高上字調”來說明，這部分內容是工尺七調皆有升高半音平行七調共十四調，依次類推，在工尺字前加前綴“高”。

上編卷二《弦音旋宮轉調》篇的弦旋宮圖譜以聲名調，一均七聲為七調，平行半音七調加前綴“清”，構成兩均十四調。?《弦音旋宮轉調》，《御制律呂正義》上編卷二，第83–90頁。

以上舉例意在說明《律呂正義》從理論上試圖將“康熙十四律”以陰陽兩均結構貫徹于管、弦音樂實踐。但是“康熙十四律”陰陽兩均是否符合音樂運動規律需要進行樂律學分析，其與七聲音階的音樂實踐不符之處主要體現在兩均的徵位和清宮位。表1中呈現“康熙十四律”規定的五聲二變音階結構與常識相悖，宮——徴之間含四全音，宮——清宮之間含七全音。因此律學分析的重點是辨析清宮位和徵位兩支管的相對音高是否符合純八度、純五度的聲學規定，進而分析“康熙十四管律”的特點。

《律呂正義》上編卷一論述了兩種律管，一種為同徑管，另一種為異徑同形管，下文分別對這兩類數據進行分析。

二、同徑管數據的律學分析

有很多文章認為十四律為不加管口校正的管律。?參見李來璋：《康熙與十四律》，《黃鐘》，1996年，第1期，第19-23頁；趙玉卿：《也論“康熙十四律”》，《黃鐘》，2008年，第4期，第187-194頁；漆明鏡：《試從〈御制律呂正義〉議“康熙十四律”》，《文化藝術研究》，2012年，第2期，第117–122頁。但是管口校正是氣鳴類樂器不可改變的物理現象，因此對《律呂正義》這組律管數據進行分析時，要將管口校正考慮進去，從理論上了解這筆數據客觀上會構成什么樣的音列。

上編卷一《定律呂之長損益相生》?詳細論述參見《定律呂之長損益相生》，《御制律呂正義》上編卷一，第11–12頁。“以古尺言之，黃鐘九寸，三分損一，得六寸為林鐘。林鐘三分益一，得八寸為太簇。太簇三分損一，得五寸三分三厘三豪三絲三忽三微三纖有奇為南呂……”《定律呂之積損益相生》?詳細論述參見《定律呂之積損益相生》，《御制律呂正義》上編卷一，第13–15頁。“黃鐘古尺之積八百一十分，三分損一得五百四十分為林鐘，林鐘三分益一得七百二十分為太簇，太簇三分損一得四百八十分為南呂……”兩篇在已知黃鐘管數據基礎上對其管長、管體積進行三分損益相生，生出其他十一支同徑律管的數據。黃鐘管數據來自上編卷一《黃鐘律分》?詳細論述參見《黃鐘律分》，《御制律呂正義》上編卷一，第8–9頁。“以橫黍之度比縱黍之度即古尺之比今尺，以古尺之十寸（即橫黍一百之度）為一率，今尺之八寸一分（即縱黍八十一之度）為二率，黃鐘古尺九寸為三率，推得四率，七寸二分九厘，即黃鐘今尺之度也”。《定黃鐘縱長體積面冪周徑》?詳細論述參見《定黃鐘縱長體積面冪周徑》，《御制律呂正義》上編卷一，第10–11頁。“正方面積以開平方，得三分三厘八豪五絲一忽，乃黃鐘古尺之徑數也。……如求面冪，則以今尺長七寸二分九厘歸之，得面冪五分九十厘四十九豪，如法求徑，得二分七厘四豪一絲九忽，是為黃鐘今尺之徑數。”兩篇，管長古尺數據為八寸一分，今尺為七寸二分九厘；管徑古尺數據為三分三厘八豪五絲一忽，今尺數據為二分七厘四豪一絲九忽。

……古今尺度雖各不同，而律之長短自不可更……?《黃鐘律分》，《御制律呂正義》上編卷一，第8頁。

……古尺之度所生律呂其分寸如彼，今尺之度所生律呂如此。古尺之度為數多，今尺之度為數少……?《定律呂之長損益相生》，《御制律呂正義》上編卷一，第12；13頁。

這兩段陳述的內容意為，雖然古今尺度長短有異，但律管的長度是不可變的。從文中申論可見這個數據上承蔡元定《律呂新書》所記，意為黃鐘律高不可變，相繼而定十二律音高也是穩定的。

《定律呂之長損益相生》一篇記載了今尺和古尺兩組不同數據，并有圖（圖略）?《定律呂之長損益相生》，《御制律呂正義》上編卷一，第12；13頁。輔助說明，筆者將原圖所示十二律的古尺、今尺長度轉錄于下表中。

文中所述“今尺”即清營造尺，一尺長32厘米?吳慧：《新編簡明中國度量衡通史》，北京：中國計量出版社，2006年，第146–147頁。“清營造尺（何工尺、部尺）長32厘米；律尺之長即為32厘米乘以0.81，即25.92厘米。”，將原文律管數據換算為現代長度，運用開管頻率公式?韓寶強：《音的歷程：現代音樂聲學導論》，北京：人民音樂出版社，2016年，第126–130頁。徐飛：《朱載堉異徑管律的物理證明》，《中國音樂》，1996年，第3期，第5–7頁。原長度數據轉換為頻率，管口校正包含其中，繼而獲得律學分析結果。

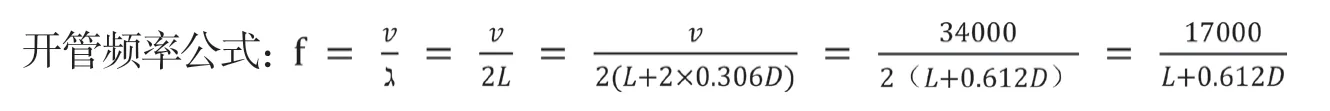
上列頻率公式中：f為頻率，v為管內聲速（取34000cm／s），?為波長，L為律管長度，D為律管內徑，開口管可取的管口校正數為0.306，此康熙律管為開口管，故乘以2（計算過程略）。表3以表2中今尺數據為基礎進行樂律學分析，包含今尺數據（單位：寸）、現代長度（單位：cm）、各音頻率數（單位：Hz）、各音相對音高（音分數，單位：cent）。

表2 十二律尺度（單位：寸）

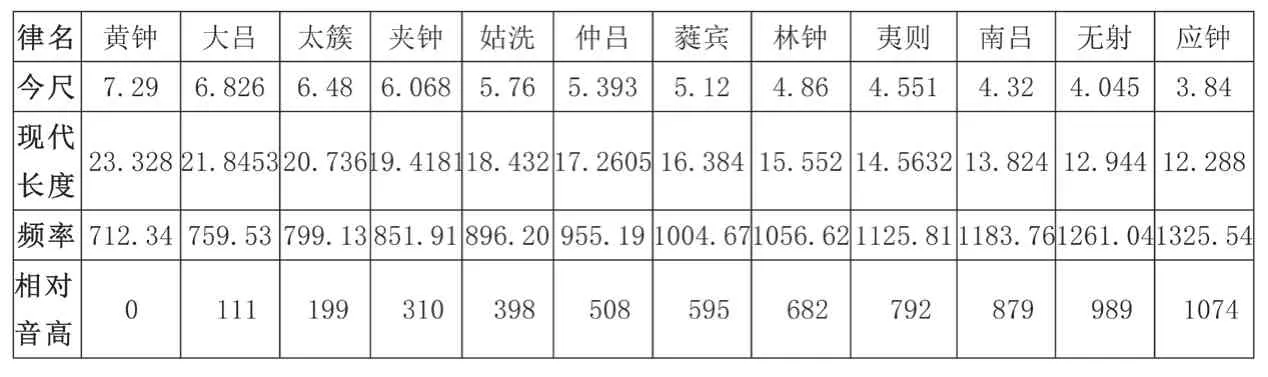
表3

繼而將表1中黃鐘均、大呂均與此數據整合。黃鐘均和大呂均兩組分別還需半黃鐘、半太簇；半大呂、半夾鐘等律的長度。

若夫正黃鐘與半黃鐘不相應者，取正黃鐘管式平分之為半黃鐘之度。其正黃鐘九寸之度，自吹口至管底九分九折，而抵一旁者值半黃鐘之四寸五分，而界于九分之四分五分之間，與界線所觸內周整分之度不合，是以其音不應。?《明管音弦音全半應聲之不同》，《御制律呂正義》上編卷二，第44；45頁。

這段話說明，《律呂正義》以管長定律名，因此半黃鐘管長是黃鐘管長的一半，古尺九寸之半為四寸五分，即今尺三寸六分四厘五毫。

又據“管律同徑者……取其九分之四則聲相應”?《明管音弦音全半應聲之不同》，《御制律呂正義》上編卷二，第44；45頁。，可知宮音長度×=清宮（半太簇）長度，7.29寸×=3.24寸。

半大呂、半夾鐘兩律的長度同此推導而出。所出長度并換算為現代長度，即如下二表，包含現代長度（單位：cm）、各音頻率數（單位：Hz）、各音相對音高（單位：cent），平均律全音遞進（單位：cent）四項數據。

前文兩均為相差一律（半音）平行關系，陰陽清濁對應，結構相同，但音高略有差異。從各自相對音高數據可見，大呂均中的變徵、徴、羽諸音比黃鐘均偏低較多，兩均中的變宮和清宮音與傳統音階的音級規定性之間差異明顯過大，所謂高八度音則高出音，可見《律呂正義》的數據與作者的主觀設想并不完全吻合。但宮——徴含四全音，宮——清宮含近七全音，與上節表1的結構一致。大呂均數據偏差略大。

“七全音說”來源于陽律全音階和陰呂全音階，但上表數據顯示出其不可聽性，而且這樣的七全音音階也全無實踐基礎。

十四律管長的產生依照三分損益法，但經過驗算，這組數據呈現出“康熙十四管律”既不是三分損益律，又以“陰陽類從”制造了一個不同于傳統七聲音階的音列。原文中以單維長度三分損益法作為同徑管律計算基礎，是“律呂三分損益上下相生之法，誠千古不易之至理也”?《黃鐘轉生律呂》，《御制律呂正義》上編卷一，第7頁。背景下的選擇，但律管發聲的振動體是圓柱型而非線型，所以單維長度的計算結果在圓柱體律管上必然不可聽。

陰陽兩均基礎結構的重點在于以與均主相隔四全音之律為徴，如黃鐘均之“夷則為五聲，以徵聲應”；與均主全、半相應者長度比為9∶4，于是“半太簇為清宮，而與黃鐘應”?同注⑤，第18頁。。這樣就形成宮、商、角、變徵是連續四個全音，按照十二律結構，蕤賓、夷則、無射、半黃鐘之間亦為連續四個全音。“康熙十四管律”規定蕤賓、夷則分別為變徴到徴，實際上已改變了七聲音階之間的全、半音規定性。十四律以單維長度定律呂，卻又將這套數據運用于圓柱體律管，必然導致林鐘管不是黃鐘管的純五度，半黃鐘管也不是黃鐘管的高八度。但十四律的黃鐘均和大呂均又要求保持與傳統七聲相同的稱謂，于是機械地填充了七聲聲名，進而產生了夷則為徵、半太簇為清宮。如此一來，定會形成一個超八度的結果。可見“康熙十四管律”將律與聲兩個不同層面的概念相混雜，一均七聲與音樂實踐不符，音亦不準。

綜上可見，如果以這一組數據制作律管，理論和實踐上都無法構成符合“康熙十四律”文字敘述所規定的音高關系，構成的音階不可聽。或許這才是雖有對《律呂正義》奉承之語，卻鮮見實踐從之的緣由。

三、異徑同形管數據的律學分析

《律呂正義》認為律管應是同徑管，見下列文字：

律呂之見于史志者，其說不一。有主同徑者，有主不同徑者。夫惟徑之同，乃得其長短之異，而聲字之清濁，賴之以辨。使徑不同而長短又異，則成同形十二律呂，皆如一黃鐘矣。故同徑之說，乃十二律呂之定論也。?《十二律同徑倍半生聲應五聲二變》，《御制律呂正義》上編卷一，第21頁。

但這段文字還提到“徑不同而長短又異”的十二律管，稱其與黃鐘管同形。“康熙十四律”的設計并非僅有同徑管。在上編卷一《黃鐘加分減分比例同形得聲應十二律呂》篇，將黃鐘管的形制按照不同倍、分比例放大縮小而得到28支律管，將這套定律器的音域放大到兩個八度。由于所得律管的管徑數據不同，其本質為異徑管。詳見原文：

凡審樂音必協之十二律呂，而制樂器則一本于黃鐘。即黃鐘一徑別其長短為十二律呂，復助以倍半而得五聲二變之全乃律呂之體。即黃鐘本積加分減分比例成同形管，而得各等黃鐘之長與徑。又每一等黃鐘本形內各具十二律呂之分，各有五聲二變之音，是為律呂之用有體以立，其本有用，以盡其變，然后器數而聲音備焉。?《黃鐘加分減分比例同形得聲應十二律呂》，《御制律呂正義》上編卷一，第27頁。

這段話是說以黃鐘律管為基礎，制作出長短有別的十二支同徑管，再增加兩支陰陽同類的半律，以備平行兩均的五聲二變之用。這個內容與“審定十二律五聲二變”相呼應。又以正黃鐘管的體積為基礎，按照一定比例加減體積制作出一系列長短有別的異徑管，稱其為同形管。每一支同形管又各自為本，制作出長短有別的十二律管，各備五聲二變。

接著，《黃鐘加分減分比例同形得聲應十二律呂》詳述“同形管”數據之變的基本模式：

今以正黃鐘之積為本，大而加分，小而減分，皆與黃鐘之長與徑相比成形，故曰同形。其大者加至八倍，則長與徑各加一倍（注略）。小者減至八分之一，而長與徑各減一半，其余諸管因用黃鐘本積加分減分之不同，故長與徑亦隨之而各異。?同注?，第24；27；24；24頁。

這段是說，比正黃鐘管低的各管以黃鐘管體積、長、徑數據為基礎而有一定比例之規地增加；比正黃鐘管高的各管以黃鐘管體積、長、徑數據為基礎而有一定比例之規地縮減。所以與上一篇《十二律同徑倍半生聲應五聲二變》集中陳述的同徑管，這里的核心是異徑。

《黃鐘加分減分比例同形得聲應十二律呂》篇后有圖（圖略）?同注?，第24；27；24；24頁。列出各同形管與十二律呂、五聲二變、工尺譜字的對應。此圖以正黃鐘之管為核心，制作兩個八度的29支異徑管，現將其內容轉錄于表格，便于分析：

《黃鐘加分減分比例同形得聲應十二律呂》篇對求徑之法、求長之法亦有詳細說明并列出所有同形管的徑、長數據：

至于求徑之法，黃鐘本積與黃鐘加分減分積數之比，即如黃鐘之徑與黃鐘加分減分徑數之比也。故以正黃鐘之積為一率，正黃鐘之徑自乘再乘為二率……以今或加分或減分之積為三率，推得四率立方開之為所求之徑……?同注?，第24；27；24；24頁。

求長之法與上述相同，只是對應維度改“徑”為“長”。

根據前文“其大者加至八倍，則長與徑各加一倍，小者減至八分之一，而長與徑各減一半”?同注?，第24；27；24；24頁。，設同形管體積倍數為N，同形管徑、管長倍數為x：

∵同形：管徑和管長同時放大或縮小相同倍數。

綜上，N倍黃鐘管為正黃鐘管體積的N倍，是正黃鐘管管徑和管長同時放大倍的結果。

將此結果帶入求徑之法、求長之法可證明原文“四率”等式成立。求徑之法、求長之法進而可簡略為所求管徑為倍黃鐘管徑，所求管長為倍黃鐘管長。帶入頻率公式，求N1倍同形管與N2倍同形管之間的頻率比：

根據原文提供的數據，將表6分為四個表格進行樂律學分析，分配方案為：加分欄陰陽二分，減分欄陰陽二分，依次如下：

徑、長已換算為現代長度（單位：cm）。表格還包括頻率（單位：Hz）、相對音高（音分數，單位：cent）數據。

表6中左右兩個單元共有29個管長數據，八倍黃鐘管、黃鐘管分別是正黃鐘管的低八度和高八度管。為了檢驗“黃鐘加分減分比例同形”原則與“十四律五聲二變”結構是否自洽，按照前述積、管長、管徑縮放公式，添加“減分同形管之大呂均”之“清宮”數據，即黃鐘倍管的高八度管黃鐘管。通過律學分析，這兩組八度的律管內部結構一致（黃鐘均表7、表9及大呂均表8、表10），因此以加分異徑同形管的黃鐘均、大呂均（表7、表8）為例，與同形管黃鐘均、大呂均（表4、表5）進行對比。

表4 同徑黃鐘均管律學分析表

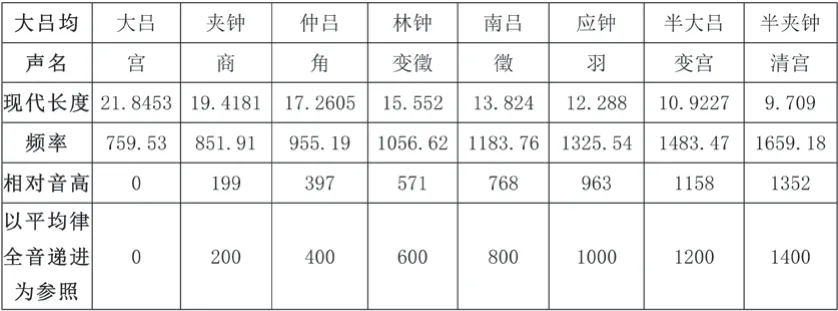
表5 同徑大呂均管律學分析表

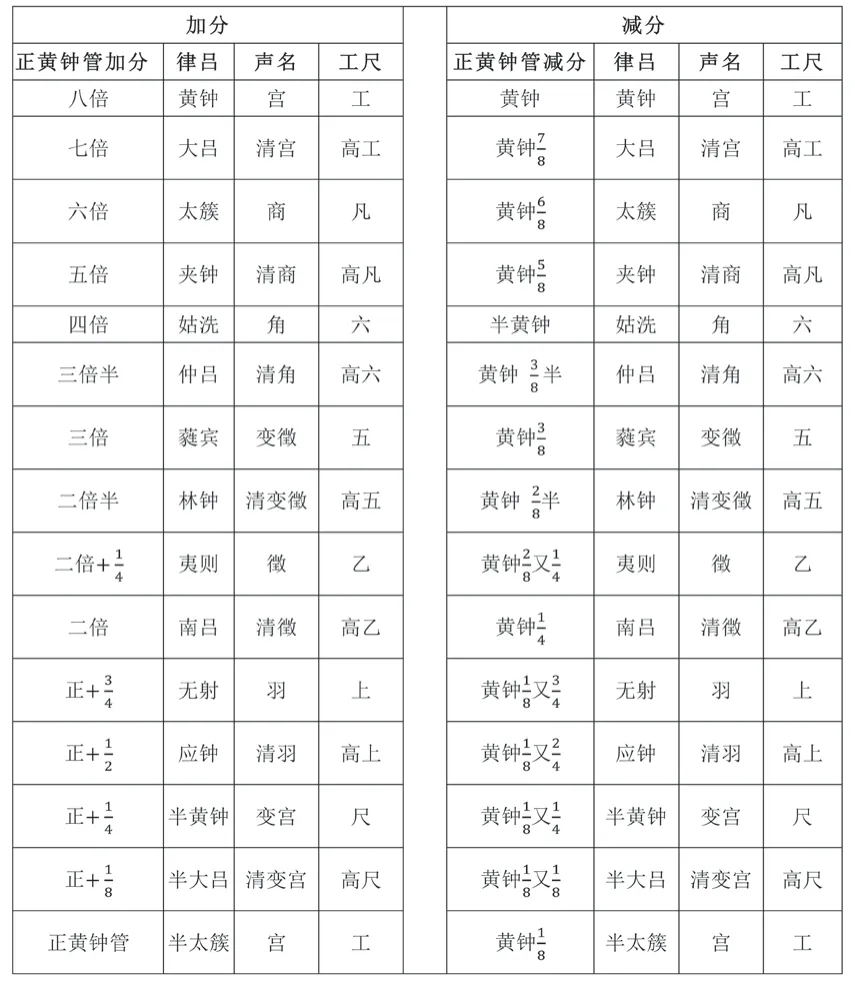
表6 黃鐘加分減分比例同形得聲應十二律呂

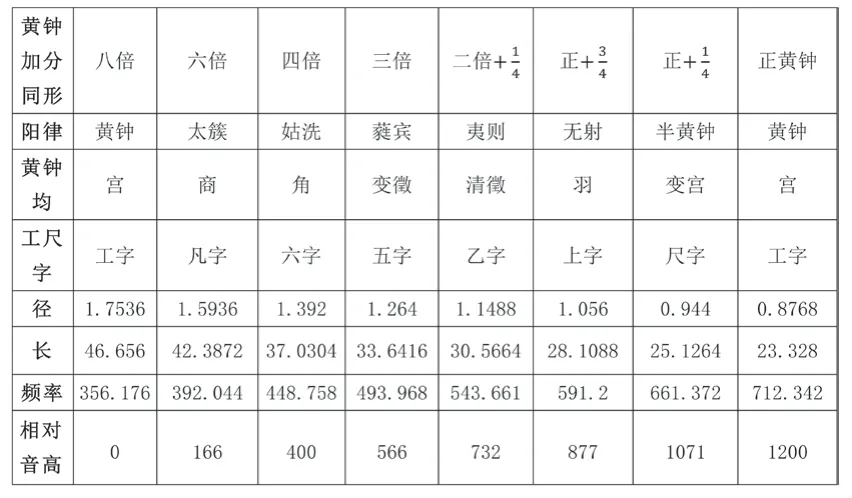
表7 加分異徑同形管之黃鐘均

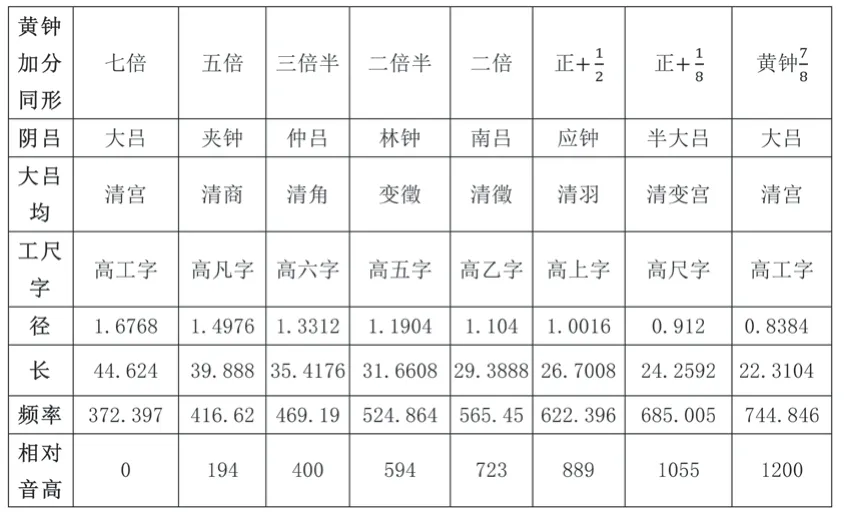
表8 加分同形管之大呂均

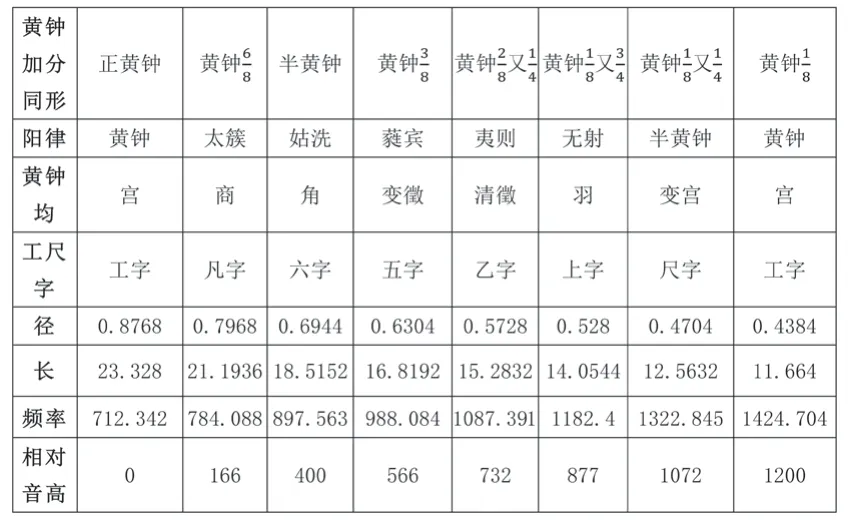
表9 減分同形管之黃鐘均

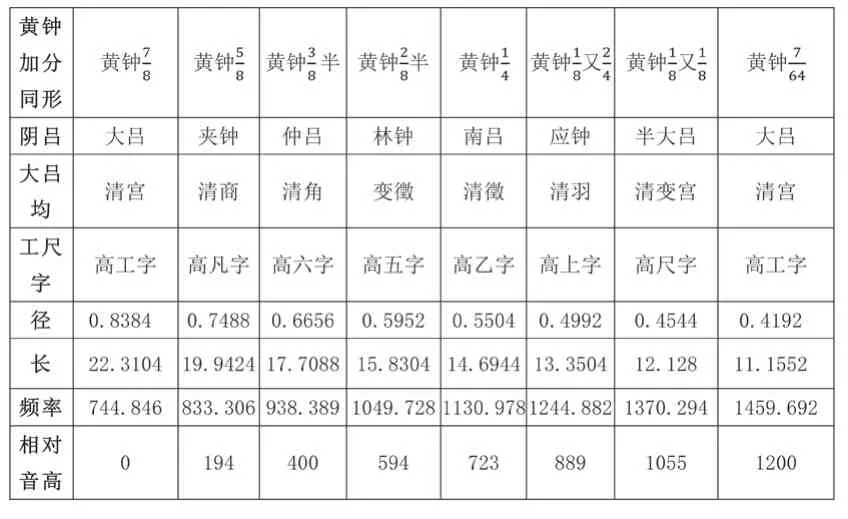
表10 減分同形管之大呂均

29支異徑同形管的數據也被制作出“同形管聲應律呂聲字表”，這是為涵蓋盡量廣闊的音域，為各式各樣管類樂器的音高設置提供依據。原文更是將體積倍數擴展大至六十四倍，小至六十四分之一倍。

今以所定正黃鐘為本，大而八倍或是更加至六十四倍，小而八分之一或更減至六十四分之一，其間同徑同形之管，凡六百九十有六，則律準律通，洞簫長笛豈能出其范圍也哉。?同注?，第27；28頁。

下舉“八倍黃鐘之管聲應黃鐘之律宮聲工字”（圖略）?同注?，第27；28頁。為例。圖中包括詳細的八倍同形管的積、徑、長以及以此為律本的十二律同徑管長度。黃鐘管從管長今尺七寸二分九厘、管徑今尺二分七厘四豪一絲九忽的圓柱體擴展為一系列異徑異長同形管。《律呂正義》在29支同形管基礎上各自生十二律同徑管，將同徑管和異徑同形管相互連接構成一個龐大的律管系統。因此比較兩種律管有利于我們認識《律呂正義》對“康熙十四管律”的全面設想。

經過律學分析比較，同徑管和異徑同形管的異同點如下：

1.相比同徑管宮——宮之間超過純八度的框架，異徑同形管的宮——宮之間則是純正的八度關系。按照構成純八度的兩管頻率比為得，即同形兩管體積倍數為8就構成純八度音程。所以異徑同形管無需以9∶4管長比值來界定純八度關系，陰陽兩均也不存在“黃鐘聲應半太簇、大呂聲應半夾鐘”。

2.異徑同形管相比同徑管還出現了平均律音程，上表宮角之間為平均律大三度，表3.1中更有數次獲得平均律音程的契機，如四倍管與八倍管之間頻率比為，七倍與三倍半管之間為。另外八倍管到二倍管、正黃鐘到黃鐘倍管之間是四全音，按照律呂標記是平均律增五度，頻率比為。平均律音程是“同形”生律過程中出現的偶然情況，《律呂正義》的作者顯然并沒有意識到這些音程關系。

3.異徑同形管和同徑管一樣，宮——徵間也不構成純五度關系。若同形管宮——徵之間為純五度，黃鐘均徵管倍數應為，而大呂均清徵管的倍數應為。異徑同形管無法產生純五度的原因與體積倍數劃分有關。

《律呂正義》在整數倍數上進一步細分異徑同形管體積倍數的思路是二分、四分、八分，原文如下：

今則高半音，而應蕤賓之律，是知管體漸小，聲音易別于三倍之積，復加正黃鐘之半積，始應仲呂之呂，于是半積之理生焉。……二倍黃鐘之管，聲應南呂之呂，而二倍半二倍之間，始應夷則之律，乃以半積復半之，是為四分之一，加于二倍之內，其分適合，于是四分之一之理生焉。……此管與正黃鐘最近，欲取合清變宮之分，則以四分之一復半之，為八分之一加于正黃鐘之分，其聲始得，于是八分之一之理生焉。?同注?，第25頁。

由于細分倍數的思路是二分、四分、八分，而非三分、九分、二十七分，所以異徑同形管無法產生純五度。

4.同徑管兩均結構為平行關系，但是異徑同形管的兩均不可能完全平行。同形管兩均除了徵位管、清宮位管，其他管與均主管的體積倍半關系不一致，比如六倍管和五倍管同為商聲，八倍管為六倍管的倍，而七倍管為五倍管的倍。這種差異導致兩均頻率比一定不同，即黃鐘均五聲二變的音階結構不同于大呂均五聲二變的音階結構。所以，同形管兩均倍數劃分決定了兩均不可能完全平行。

從以上律學分析可見，同形管產生的基礎不是三分損益法而是正黃鐘管“同形”放大縮小，因此兩種管從本質上完全不同，同形管組與同徑管組一樣無法產生純五度，但是具備純八度。《律呂正義》對倍數的選擇導致同形管組兩均無法完全一致，與“康熙十四律”陰陽兩均的文字描述相悖。

結 語

通過分析，兩種律管數據呈現的律學本質與陰陽兩均文字描述有矛盾之處。無論是同徑管還是同形管的兩均音階理論上都不具備可聽性。“康熙十四管律”核心為陰陽兩均結構，《律呂正義》的制律思路是以十二律呂為基礎，在強調樂學結構的過程中形成了十四個律位的格局。因此，“康熙十四管律”不是一種律制，而是出于“管音弦音全半聲之不同”“陰陽以類不雜”的權宜之舉。

《律呂正義》對同徑管、同形管的討論以及在此基礎上建立的理論系統呈現出完整流暢的思路。陰陽兩均貫穿始終，每支管聲名律呂譜字都以此為標準進行標識。兩種律管關系緊密，同形管由同徑管的形制以不同倍、分比例放大縮小而得，同徑管由同形管管長三分損益而得，通過律名、聲名、工尺譜字互相交織，內在理論邏輯一致。

三分損益法是兩千年來的正統之法，至明朱載堉提出“新法密率”，破三分損益法、破黃鐘九寸、破隔八相生，此學術主張在《律呂正義》的撰寫者眼中是離經叛道的。所以，作為清朝官方音樂典籍，《律呂正義》強調三分損益法是“千古不易之至理也”?同注?。。“康熙十四管律”以管長三分損益產生同徑管的方式維護三分損益法的正統地位。《律呂正義后編》在“樂問二”中指責“載堉概舍先儒而不之信，任其私智，創為新法，乃曰蓋皇帝云然”?《御制律呂正義后編》，載《景印文淵閣四庫全書》（第218冊），臺北：臺灣商務印書館，1986年，第489頁。，可見清代官方律學強調經學的傳統立場，反映出清朝統治者對“聲音之道與政通”儒家思想的繼承。

《律呂正義》對“康熙十四管律”的表述展現出強烈的理論建設意識。《律呂正義》的撰寫者以一系列的理論設定來自圓其說，將三分損益法與陰陽兩均、隔八相生、管長比“9∶4”等等內容結合起來，構建出六百九十六支律管的龐大系統來滿足新朝定律的政治需求。因此，“康熙十四管律”有其存在合理性。