基于線性譜聚類超像素分割和聯合稀疏表示的高光譜圖像分類算法
魏宏超,王永麗,丁曉云,陶菊亮
(山東科技大學 數學與系統科學學院,山東 青島 266590)
隨著遙感傳感器技術的不斷發展,高光譜圖像(hyperspectral image,HSI)以精細的光譜分辨率得到越來越廣泛的應用[1],例如環境監測[2]、礦物勘探與分析[3]、城市發展分析[4-5]等等。HSI在各大領域的廣泛應用,使得圖像分析處理也變得越來越重要。
分類作為高光譜圖像分析處理的重要手段之一,其目標是對每一個像素進行準確的類標識。目前,高光譜圖像分類主要分為有監督分類、半監督分類和無監督分類三種。稀疏表示(sparse representation,SR)算法[6]作為有監督分類的一種,以其較好的分類效果在高光譜圖像分類中得到廣泛應用[7]。考慮到在同一類別的像素應具有相似的光譜特征,SR算法采用屬于同一類別的少量訓練樣本線性表示每一個待分類的測試樣本,計算對應的稀疏系數,然后求解兩者的最小殘差,并以此確定所屬類別。
傳統的SR算法只考慮HSI的基本光譜信息,忽略了像素間的空間鄰域信息,容易導致高光譜圖像分類結果不平滑[8]。為了克服這個問題,一些學者引入HSI在空間分布上的一致特性,提出將光譜信息和空間信息相融合的分類算法。Chen等[9]利用相同訓練樣本表示領域內的所有像素,充分考慮像素間的空間鄰域信息,提出聯合稀疏表示(joint sparse representation,JSR)算法;Fang等[10]在多尺度空間上,通過自適應的稀疏矩陣實現對HSI的精準分類。然而,通常情況下,HSI地物種類非常復雜,不同種類間不一定完全排斥,導致其空間分布的一致性并非普遍存在。同時,高光譜圖像的像素間還普遍存在同類異譜和異類同譜的現象,導致分類精度降低。
同時,諸如SR這類監督分類算法通常需要大量的訓練樣本,而在實際應用中獲取大量的訓練樣本費時費力,不容易實現,影響分類精度。針對這一問題,一些學者提出無監督分類算法,該類算法的最大優點是不需要高光譜圖像的先驗信息,例如K-means算法[11]、均值漂移(mean-shift)算法[12]和基于密度的帶噪聲的空間聚類方法(density-based spatial clustering of applications with noise,DBSCAN)[13]等。相對于監督分類必須以圖像存在樣本標簽為前提,非監督分類的分類效率比較高效,但主要缺陷是精度不高,對于參數的敏感度極高,聚類效果的穩定性也很差,并且隨著高光譜圖像維度的增加分類效率會下降。
針對以上問題,本研究在文獻[14]的基礎上提出一種基于線性譜聚類(linear spectral clustering,LSC)超像素和譜聚類相融合的相關系數聯合稀疏表示算法。該算法通過LSC超像素分割從全局上考慮高光譜圖像的數據特征,在利用高光譜圖像的光譜信息和空間信息的同時,充分考慮噪聲及區域邊界對分類效果的影響,克服了由于同類異譜和異類同譜現象導致的分類精度較低的問題,減少了類間干擾。圖1為算法執行過程,是基于LSC超像素分割、譜聚類和聯合稀疏表示的高光譜圖像三級分類算法。首先,通過主成分分析(principal component analysis,PCA)降維實現對高光譜圖像的LSC超像素分割,從分割后的超像素塊中選取一小部分作為標簽樣本進行類別標注,并將剩余的超像素塊作為訓練樣本;其次,通過K-means和譜聚類算法將訓練樣本分成兩類,按規則選取其中一類作為測試樣本,并計算測試樣本與標簽樣本之間的相關系數;然后,對選出的測試樣本進行稀疏矩陣計算,進而計算出測試樣本與各類標簽樣本的最小殘差,并將其作為所有訓練樣本的最小殘差;最后,用基于表示殘差和相關系數的決策函數對像素進行分類。
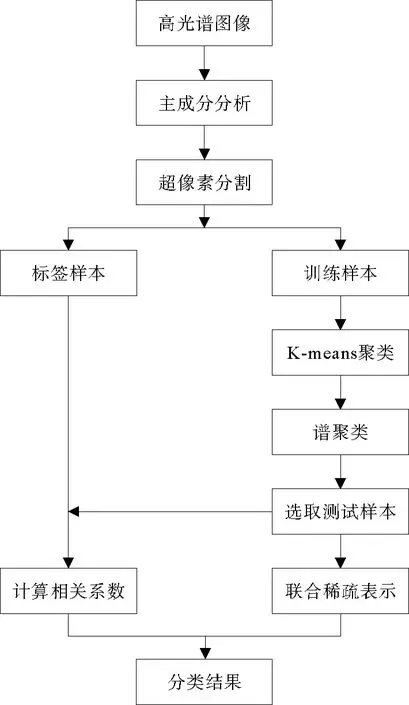
圖1 算法執行過程
1 相關工作
1.1 超像素分割技術
超像素分割是2013年提出的圖像分割技術[15],是將圖像細分割成若干統一、均勻、互不重疊的子區域,每個區域包含了一定的紋理、顏色和亮度等物理特征[16]。超像素分割利用像素之間特征的相似性,將像素進行分組并捕獲圖像的冗余信息,大大降低了后續圖像處理任務的復雜度。分割的超像素塊數越多,圖像超像素分割越細,則每個超像素包含的像素越少;反之,每個超像素包含的像素越多。圖2展示了對同一幅圖像進行不同分割數量的超像素分割結果。
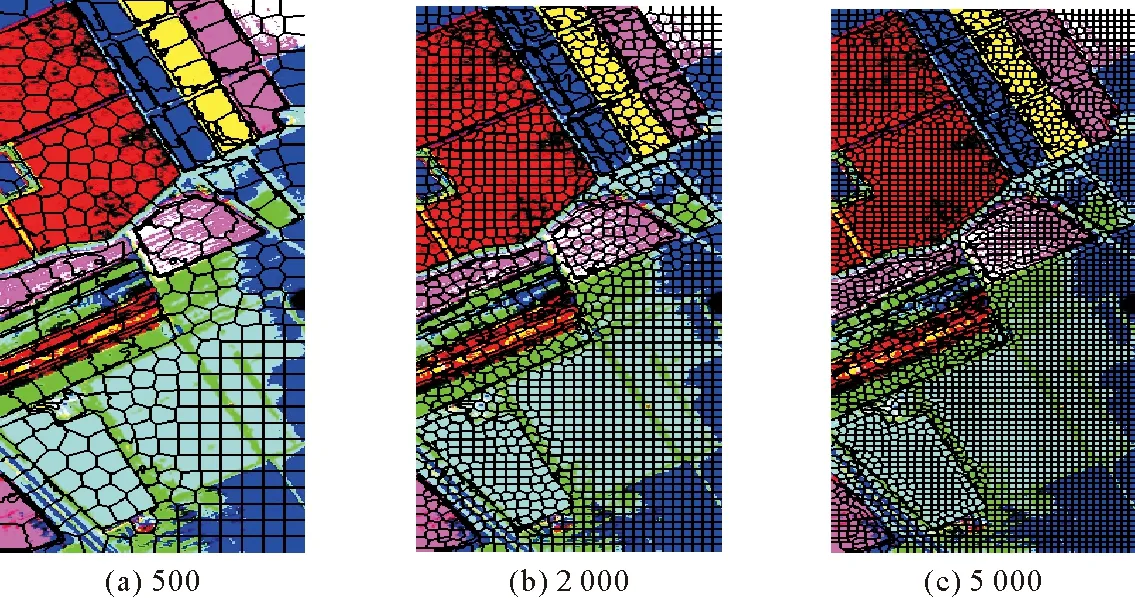
圖2 不同數量超像素分割結果
由于超像素所具備的這種同質特性,引起高光譜圖像分類研究者們的極大興趣。Fan等[17]將超像素分割集成到低秩表示中,提出一種新的去噪方法SS-LRR。Zhang等[18]為了克服利用結構信息的缺點,提出一種基于多尺度超像素的稀疏表示算法用于高光譜圖像分類。Zu等[19]提出一種基于簡單線性迭代聚類(simple linear iterative clustering,SLIC)超像素分割技術的l2,1范數魯棒主成分分析HSI分類算法。相關實驗結果表明,應用超像素分割技術進行HSI分類,不僅能解決HSI降維的問題,而且借助超像素的局部性質,可以為HSI分析提供豐富的空域結構信息。
目前,超像素分割技術主要有LSC[20]、Normalized cuts[21]、Mean shift[22]、Turbo-pixel[23]、SLIC[24]等。其中,SLIC作為一種基于局部特征的算法,以思想簡單和分割快速的優點被廣泛使用,但因其無法與全局優化信息進行有效地結合,影響了超像素分割的效果,導致超像素的邊界依附性和形狀緊湊性不理想。而LSC作為一種基于歸一化割集的圖像分割方法,利用兩種看似不同方法之間的數學等價性將像素數據顯式地映射到高維特征空間,通過橋接局部和全局的方法,有效地解決了高復雜度的全局問題[20]。與SLIC相比,LSC不僅生成的超像素能很好地適應自然圖像的紋理和結構,而且還可以捕獲全局信息,具有良好的形狀緊湊性和邊界附著力。
1.2 譜聚類算法
譜聚類[25]是一種基于圖的聚類方法,其分類思想是找到數據集中類內相似度最大而類間相似度最小的劃分。譜聚類算法可以對任意形狀的數據進行最優劃分,然而由于計算圖劃分準則的最優解是一個不確定性多項式難問題,所以對此類問題的求解通常是轉化為求解相似度矩陣的譜分解問題,利用譜分解得到合適的特征向量來描述數據的低維結構,并在低維空間中利用K-means等經典方法得到最終的聚類結果。
譜聚類算法基本思想是,首先構建樣本集的相似度矩陣W,然后通過計算W的前K個特征值與特征向量,構建特征向量空間,最后利用K-means或其他經典聚類算法對特征向量空間中的特征向量進行聚類。
由于譜聚類算法涉及降維處理,相比傳統聚類算法,譜聚類算法對高維度數據的聚類效果會更加突出。同時,譜聚類算法不需要樣本服從某種分布,在很大程度上避免了樣本空間分布假設的局限性,能夠聚類成任何樣本形狀。
1.3 聯合稀疏表示分類算法
聯合稀疏表示分類算法[26]是在假設相鄰的高光譜圖像通常由相似的物質組成,從而具有相同光譜特征的前提下提出來的,具體表述如下。
給定N個訓練樣本,設地物類別數為M,并記S={1,2,…,N},S=S1+S2+…+SM。其中,Sm為第m類訓練樣本(m=1,2,…,M)。設第i個訓練樣本的光譜向量為xi(i∈S),其字典矩陣為X=(x1,x2,…,xN),設y={y1,y2…,yt}為當前待分類像素鄰域矩陣(t為鄰域內像素總數),則關于y的聯合稀疏表示為:
(1)
式中:α=[α1,α2,…,αt],αj(j=1,2,…,t)為第j個像素的稀疏系數向量,可由α中非零元素對應的字典類型判別y在X中的歸屬;‖·‖F為F范數;‖α‖row,0是稀疏矩陣中非零行的個數,η為給定的稀疏水平。
對于式(1),采用同步正交匹配追蹤(simultanaous orthogonal matching pursuit,SOMP)算法[27]進行求解,得到稀疏矩陣α,并以此計算y被第j類字典表示的殘差
rj(y)=‖y-Xj·αj‖F。
(2)
式中:j=1,2,…,M;Xj和αj分別為X和α的第j列和第j行。則基于殘差的像素分類可以描述為:
(3)
1.4 相關系數
相關關系是一種非確定的關系,相關系數是研究兩變量間線性相關程度的有效度量。對于高光譜圖像而言,每一個像素都有n維譜段組,本研究利用簡單相關系數來計算HSI兩個像素間的相關性:
(4)
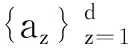
2 算法提出
2.1 LSC算法
LSC算法是在研究歸一化割集的目標函數和加權K-means關系的基礎上提出來的,是一個以五維(L,a,b,x,y)空間為基礎進行分割的超像素分割算法,其中(L,a,b)為彩色圖像轉化為CIELab顏色空間后的三維向量,(x,y)為像素坐標位置。而對高光譜圖像G∈RM×N×H,其(M,N)為像素坐標位置,H為波段數(H>3)。因此,需要對H個波段進行降維后才能用LSC算法對高光譜圖像進行超像素分割。采用PCA算法對高光譜圖像進行數據預處理,選取前3個主成分作為超像素分割的數據。
但該算法并不是在五維特征向量空間中完成的,而是利用了兩種看似不同的方法之間的數學等價性,將數據點映射到高維特征空間中以提高線性可分性。算法1給出了LSC超像素分割算法的實現步驟。其中,Vx/Vy近似等于圖像的縱橫比,t≥0.5是平衡局部緊致性和全局最優性的一個參數。在聚類合并階段,根據經驗,將小于預期超像素大小1/4的孤立小像素點與相鄰的大像素點合并。

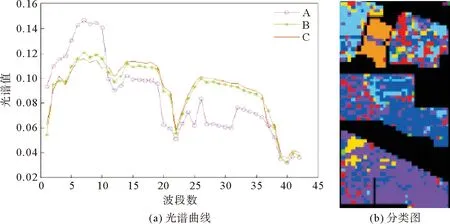
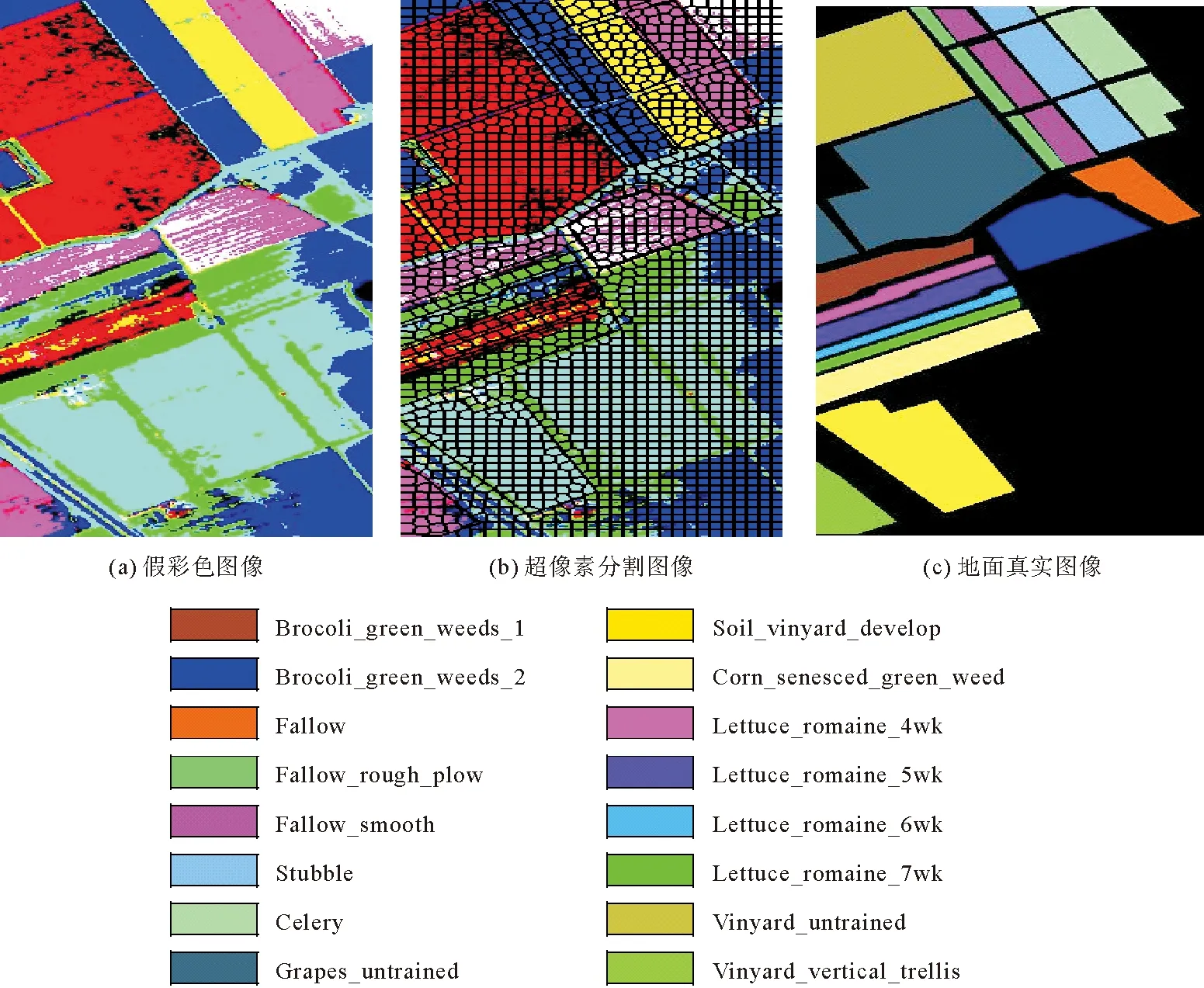
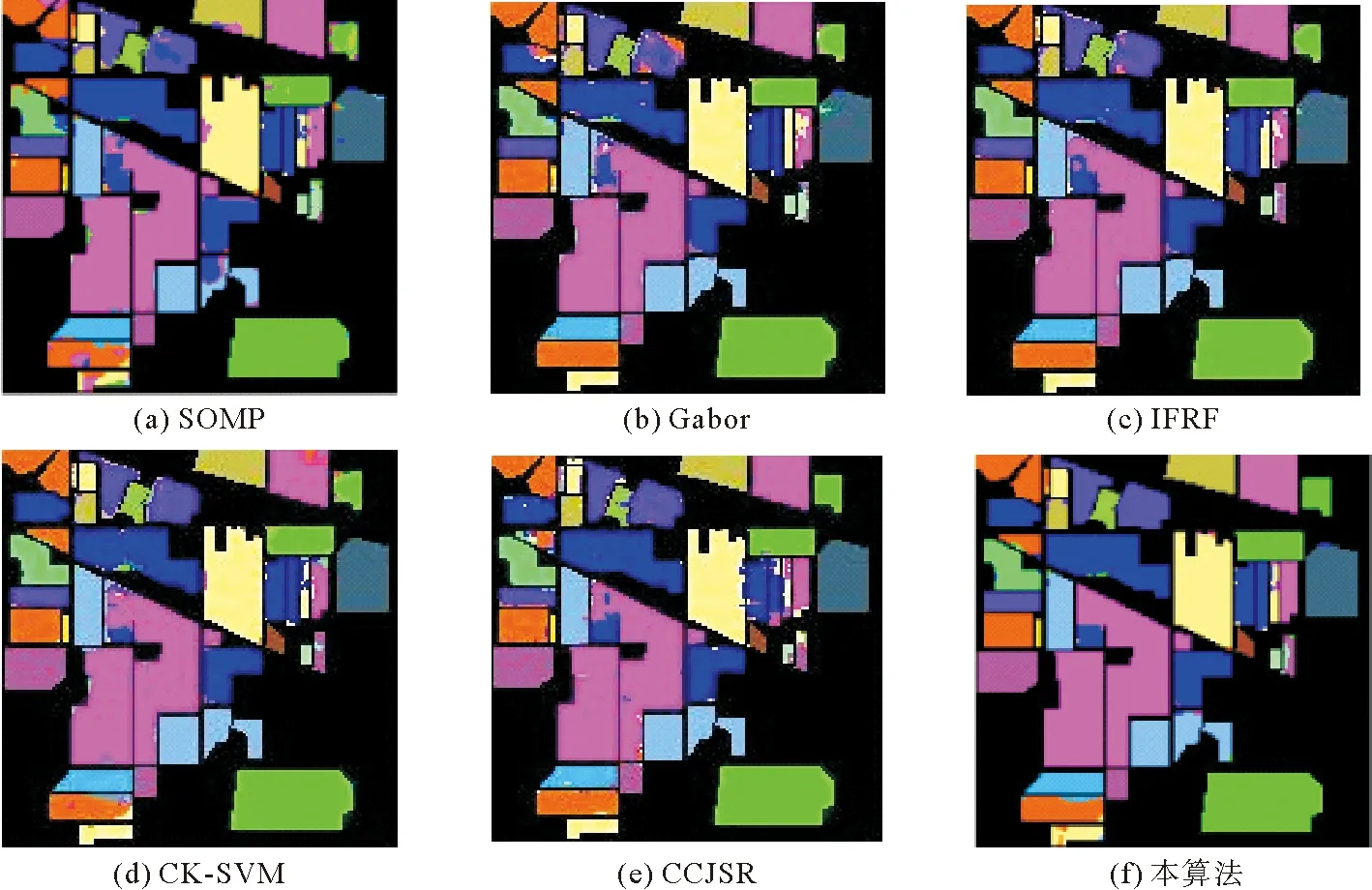
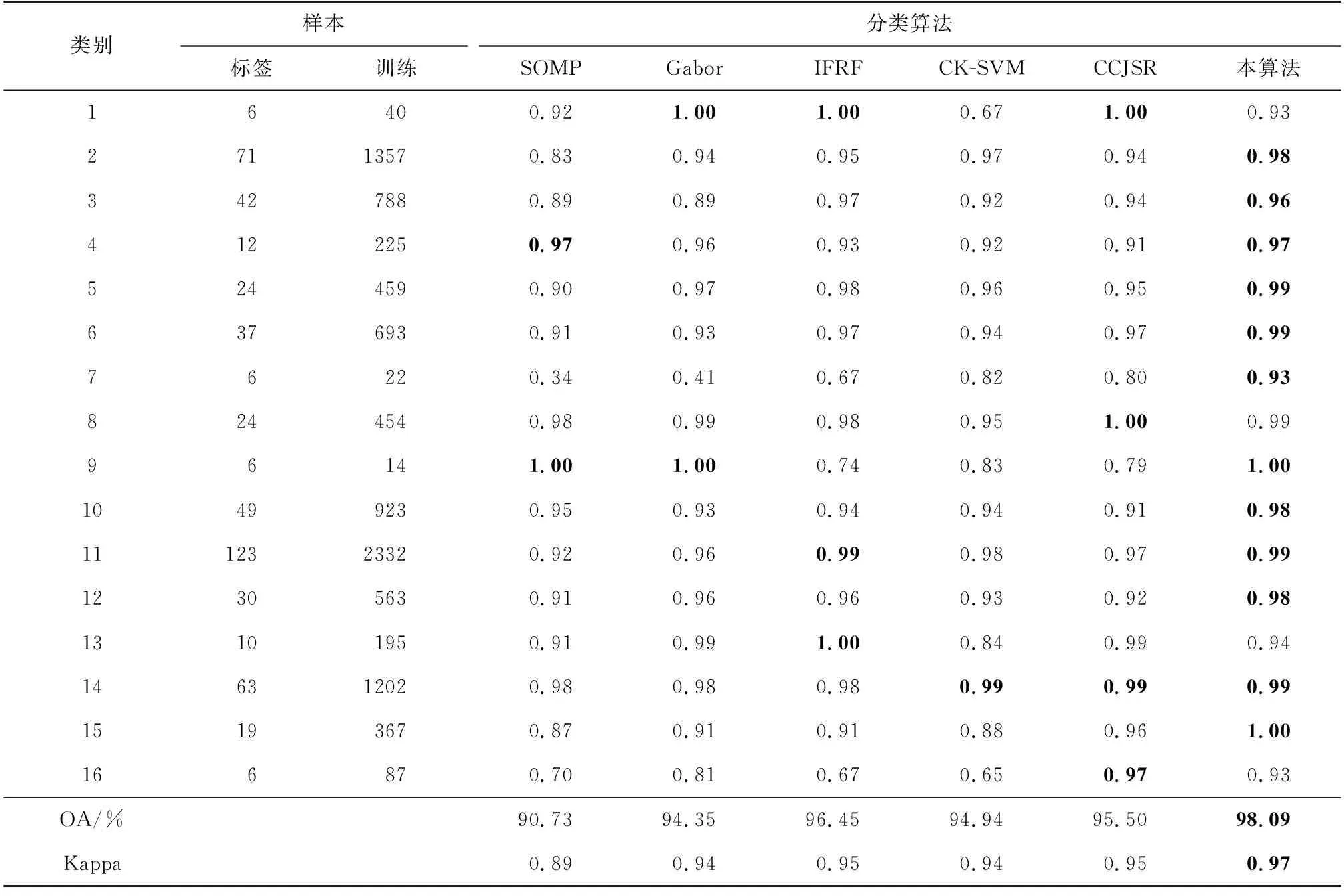
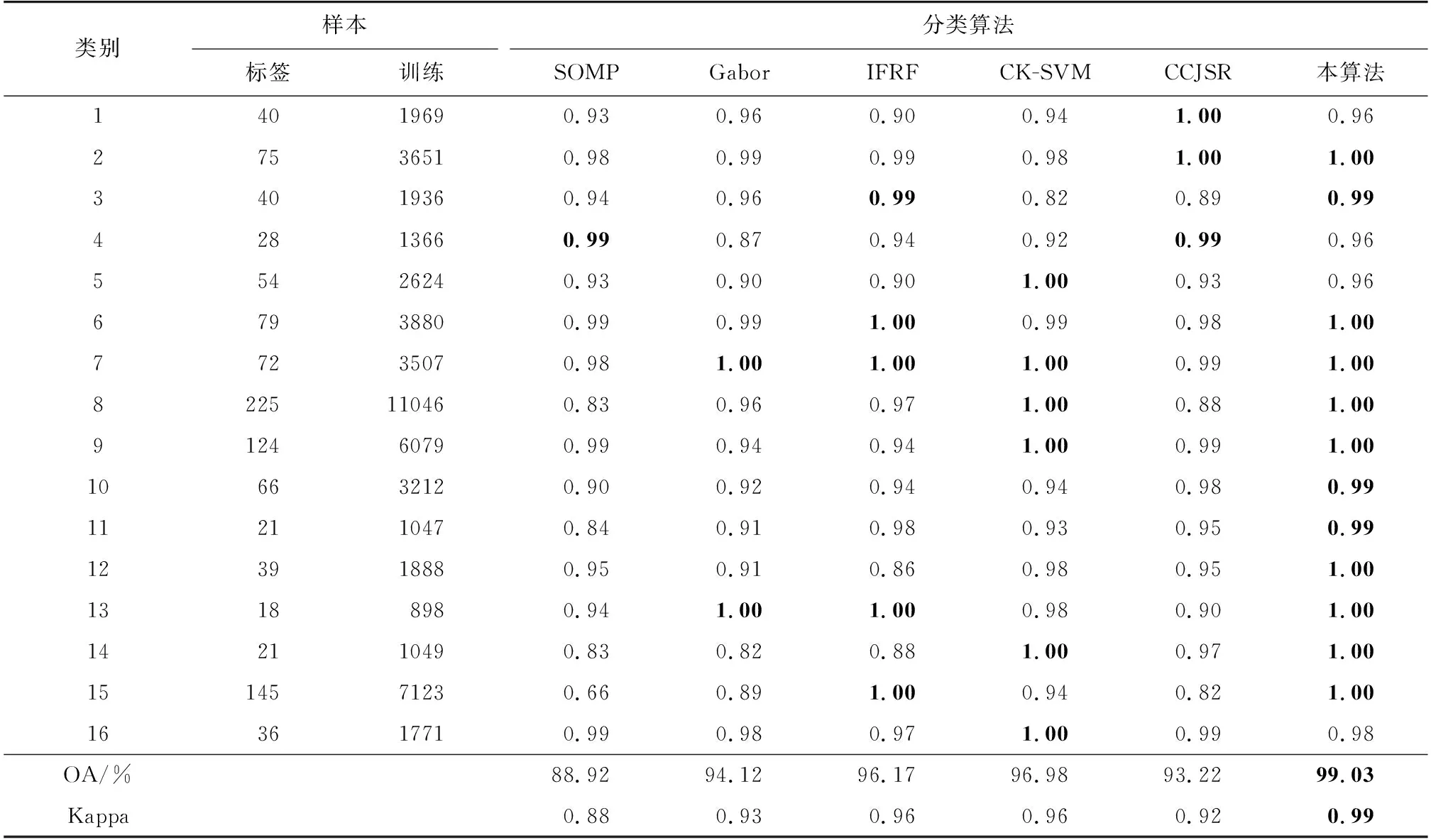
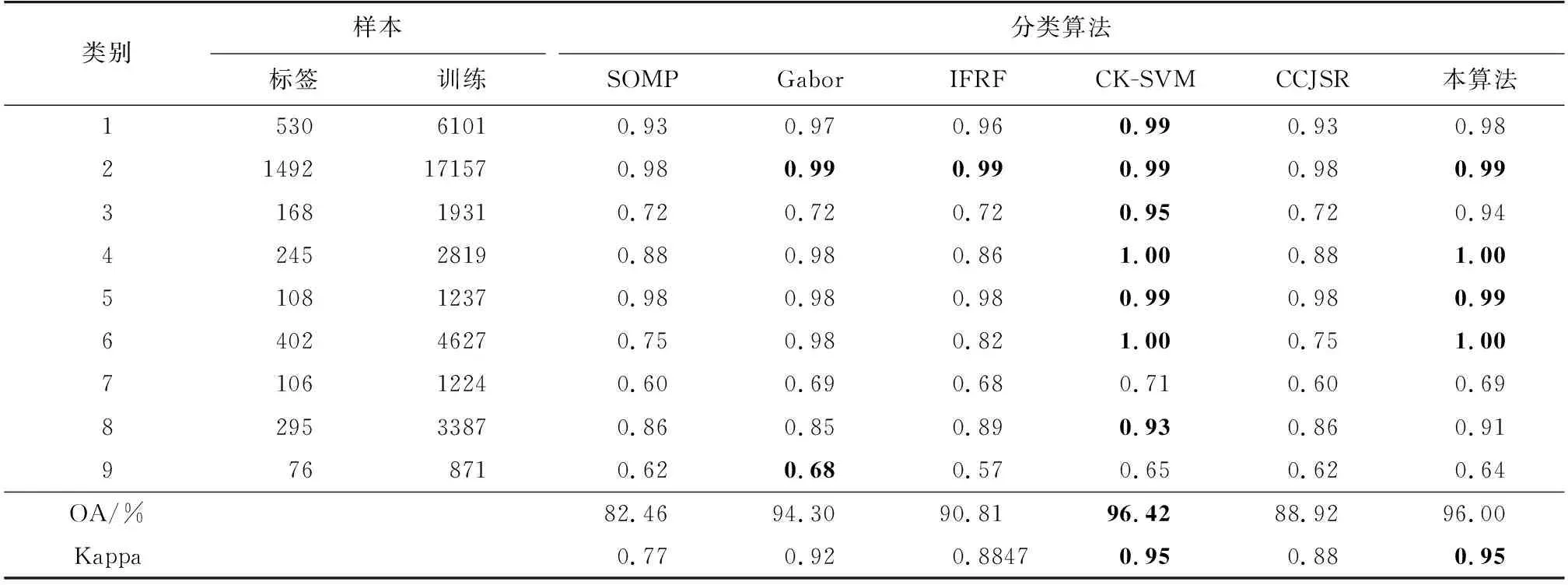
算法1 LSC超像素分割算法輸入: PCA預處理后的高光譜圖像數據,t=0.5,超像素數k初始化:1) 將每個五維像素點p映射到高維特征空間中的一個向量?(p)2) 以固定的水平間隔Vx和垂直間隔Vy在圖像上均勻采樣k個種子點3) 通過種子點初始化相應簇的加權平均值mk和搜索中心ck4) 對每個像素點p設定標簽L(p)=0,設定距離D(p)=∞迭代:1) for 每個加權平均值mk和搜索中心ck do2) for 搜索中心ck的tVx*tVy領域中的像素點p do3) 計算?(p)和mk之間的歐氏距離d4) if D 2.2.1 算法分析 經LSC超像素分割后的每一塊超像素都是在空間分布上具有一致性的區域。但如圖3所示,在高光譜圖像中同類異譜和異類同譜現象普遍存在且無法避免。圖3(a)光譜曲線圖中的曲線A和B所對應的光譜曲線存在很大的差異,但兩者卻為同一類別,即同類異譜現象;而曲線A和B所對應的光譜曲線趨勢十分相近,但兩者卻為不同類別,即異類同譜現象。當超像素塊分的較細,而超像素塊中又存在嚴重的同類異譜現象時,會導致分類結果錯分嚴重,如圖3(b)。反之,當超像素塊分的較少時,每個像素塊包含的像素數就會較多,而譜聚類構造相似矩陣和進行特征值分解的時間復雜度通常隨著像素數量的增多而增加,導致計算復雜度增加。 圖3 光譜曲線圖和分類圖 針對第一個問題,采取“少數服從多數”的選取規則,即將像素通過譜聚類分為兩類后,分別統計兩個類別的像素個數,選取個數多的一類作為聯合稀疏表示的待分類測試樣本集。針對第二個時間復雜度的問題,在譜聚類之前對待分類訓練樣本集進行一次K-means粗分類,得到相對應類別數的聚類中心,然后再對其進行譜聚類處理,這樣在不損害聚類精度的同時大大降低了譜聚類的時間復雜度。同時當超像素塊內任意一個訓練樣本得到分類標簽后,對超像素塊內其余測試像素賦值相同的類標簽,并對該部分訓練樣本進行標記剔除,使其不參與循環,通過這種策略,可以極大降低算法的時間復雜度。 2.2.2 算法實現 提出一種結合譜聚類、相關系數和聯合稀疏表示的高光譜圖像分類算法,算法2展示了該分類算法的執行過程。具體求解過程如下。 首先,為了提高噪聲點和邊界處的分類效果,利用式(4)對標簽樣本和訓練樣本間的相關系數進行計算,即 (5) (6) 根據式(1),可得稀疏矩陣 (7) 于是,每類樣本的殘差為: (8) 式中:j=1,2,…,c;c為樣本類別。 最后,根據決策函數確定每個樣本的類標簽。通過在決策函數中引入正則化參數λ,實現聯合稀疏表示和相關系數之間的平衡,得到訓練樣本y的最終類標簽 (9) 算法2 基于譜聚類和相關系數的稀疏表示算法輸入:標簽樣本Xτ=x1,j1 ,…,xτ,jτ ∈Rd×j τ,d為光譜帶個數,j={1,2,…,c}為對應訓練樣本的類標簽;訓練樣本Y=y1,…,yn ∈Rd;超像素標簽G∈RM×N;稀疏水平Sl=2;N=8;正則化參數λ;K-means聚類數K,零矩陣Z∈R1×n步驟1:1) for i=1,2,…,n2) for j=1,2,…,c3) 用式(4)計算標簽樣本和訓練樣本間的相關系數值4) end for5) 用式(5)計算corj6) end for步驟2:1) for i=1,2,…,n2) 如果Zi=0轉第3步,否則轉第10步3) 結合超像素標簽L求出yi所在的超像素塊內的訓練樣本H4) 對H用K-means聚類算法聚類為K類,并記錄對應類的類中心C5) 對類中心C用譜聚類算法聚類為2類,并統計每類的訓練樣本的數量6) 選取訓練樣本數量最多的一類W7) 用SOMP計算W稀疏系數8) 用式(7)計算W被每類訓練樣本表示的殘差,并作為該樣本的表示殘差9) 基于式(8)確定該超樣本的類標簽,并對W中與超像素塊內的訓練樣本相對應的位置的值賦值為110) end for輸出:分類結果 為了驗證所提算法的性能,選取3幅常用的高光譜圖像進行實驗,并與SOMP[27]、Gabor[28]、IFRF[29]、CK-SVM[30]、CCJSR[15]等算法進行比較。每組實驗數據集都是將原始高光譜圖像進行歸一化后得到,為了消除相關干擾,每組實驗都進行10次后取平均值。 使用3個真實高光譜遙感數據集進行實驗評價,分別是Indian Pines數據集、Salinas數據集和帕維亞大學(Pavia University)數據集。 Indian Pines數據集是在美國西北部印第安州的印度松試驗場采集的部分圖像數據。Indian Pines數據集是一個220波段的AVIRIS高光譜圖像,圖像大小為145×145像素,光譜分辨率為10 nm,空間分辨率為20 nm。但是由于第104~108、第150~163和第220個波段不能被水反射,因此一般選用剔除這20個波段后剩下的200個波段作為研究對象。該圖像是在6月份采集的,一些農作物,如玉米和大豆,仍處于早期成長階段,覆蓋率不足5%。利用現場的參考分類,將場景劃分為16個不同的類別,并且它們之間不完全相互排斥。圖4展示了Indian Pines數據集的假彩色圖像和地面真實圖像。 圖4 Indian Pines數據集 Salinas數據集是在美國加利福尼亞州的Salinas山谷獲取的圖像,是從3.7 m空間分辨率的AVIRIS傳感器上獲得的。該圖像大小為512×217像素,去除原始圖像中的20個水汽波段,最終留下剩余的204個波段。整個圖像包含了16類地物,具體分類如圖5所示。 圖5 Salines數據集 Pavia University數據集是從意大利的帕維亞大學獲得的圖像,圖像大小為610×340像素,共有115個波段,空間分辨率為1.3 m。其中12個波段由于受到噪聲影響被剔除,使用剩下的103個光譜段所成的圖像。Pavia University的假彩色圖像和相應的地面真實圖像如圖6所示,場景被劃分成了9類。 圖6 Pavia University數據集 為了比較不同分類算法的性能,選取分類精度(classification accuracy,CA)、總體精度(overall accuracy,OA)及Kappa系數3個常用HSI分類指標作為評價標準[31]。其中,CA為圖像中每個類別的分類精度,OA為總體正確分類的百分比。Kappa系數為一致性檢驗指標,CA和OA為檢查有多少像素被正確分類的指標[32]。 在3幅常用的HSI圖像上進行實驗測試,與5種已有的分類算法相比較,驗證本算法的有效性。根據Indian Pines、Salines和Pavia University圖像的類別數和不同類別對應地面真實圖像的形狀規則度,對3幅圖像分別隨機抽取每類樣本的5%、2%和8%作為標簽樣本集,其中標簽集在每次運算中都進行重新采樣,并且都是隨機選擇的。考慮到樣本少的數據集按比例抽取后可能會很小,實驗中設置每個樣本的最小閾值為6,以此平衡樣本間的差異性。對于超像素的數量,根據圖像的大小及經驗,分別設置3個HSI的LSC超像素為800、2 000和5 000。 表1~3給出了不同分類算法的10次實驗分類結果對應的CA、OA和Kappa系數的平均值。其中,表中的數據為CA值,粗體代表最佳值。圖7~9顯示了在10次實驗中最接近平均OA值的一次實驗對應的分類圖。 圖7 Indian Pines數據集分類圖 由表1~3的實驗結果可以看出,本算法性能相對優于其他算法,雖然對于Pavia University數據集的分類精度比CK-SVM算法差,但僅相差0.42%,說明本算法魯棒性相對較好。分析Indian Pines和Salines數據集的實驗結果可以發現,無論這兩個高光譜圖像每個類的樣本多少,相比其他方法,本算法的分類精度CA都保持著較高水平。對于Pavia University數據集,雖然其分類類別較少,且每個類的訓練樣本數量也最多,但其分類精度卻不是很穩定,說明對于紋理相對較清晰的高光譜圖像,超像素分割的引入,可以大大提高分類精度。對于每類區域分得比較細小、紋理相對比較復雜的高光譜圖像,由于超像素分割的邊緣契合度不是很高,導致分類精度降低。但相對于其他幾種方法,本算法仍有較大優勢,特別是相對于CCJSR算法而言,本算法無論是總體精度,還是分類精度都高出很多,也進一步說明超像素分割和譜聚類的引入提高了聯合稀疏表示算法的分類效果。 表1 Indian Pines實驗數據 表2 Salines實驗數據 表3 Pavia University實驗數據 針對高光譜圖像空間分布一致性并非普遍存在,且存在同類異譜和異類同譜現象,導致高光譜圖像分類精度大大降低的問題,提出基于線性譜聚類(LSC)超像素分割和聯合稀疏表示算法。該算法利用LSC超像素分割從全局上考慮高光譜圖像的數據特征,利用高光譜圖像的光譜信息和空間信息,并且考慮了噪聲及區域邊界對分類效果的影響,消除了同類異譜和異類同譜現象對分類精度的影響,減少了類間干擾。實驗結果表明,與其他5種算法相比,本算法不僅提高了總體分類精度,也大大提高了每個類的分類精度。特別地,LSC超像素分割以其良好的邊界依附性和形狀緊湊性,使本算法具有良好的魯棒性。 圖8 Salines數據集分類圖 圖9 Pavia University數據集分類圖2.2 基于譜聚類和相關系數的聯合稀疏表示算法
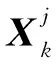
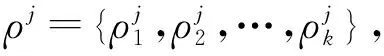

3 數值實驗與結果分析
3.1 實驗數據集


3.2 參數設置

3.3 評價指標
3.4 實驗結果分析
4 結論



