基于博弈論優化的高效聯邦學習方案
周全興,李秋賢,丁紅發,樊玫玫
(1.凱里學院 大數據工程學院,貴州 凱里 556011;2.貴州財經大學 信息學院,貴陽 550025;3.貴州大學 數學與統計學院,貴陽 550025)
0 概述
隨著大數據技術的快速發展,各類移動設備的計算及通信能力得到顯著提高。因此,基于機器學習的新型學習框架應運而生[1]。機器學習技術能夠有效提高各類移動設備的應用性能,但是需要將敏感的私有信息和數據上傳至中央服務器并對模型進行訓練,存在嚴重的隱私泄露風險、額外的計算與通信開銷問題[2-3]。為加強用戶數據信息的隱私與安全,聯邦學習[4-5]作為一種新型的分布式機器學習技術應運而生。聯邦學習使大規模的移動設備在不泄露本地數據的前提下,通過協作使用各自的數據集來訓練機器學習共享模型。聯邦學習作為一種去中心化分布式的訓練模型方法,利用各移動設備的數據采集與計算能力解決數據的隱私安全問題[6]。
由于聯邦學習不需要各類移動設備直接進行數據交換,因此在一定程度上保護了用戶的數據安全與隱私[7]。文獻[8]提出一種基于貪婪算法的聯邦學習方案,利用分布式移動設備數據和計算資源來訓練高性能機器學習模型,同時保護客戶端的隱私和安全。文獻[9]通過增強本地移動設備的計算能力減少聯邦學習通信頻率,設計典型的聯邦平均算法,通過云處理中心對局部的移動設備進行整合,大幅減少了傳輸局部模型的數量,節省通信開銷。文獻[10]通過無線網絡構造聯邦學習框架,并對其學習時間和數據的準確度進行優化,以控制用戶的數據訓練能量成本。文獻[11]提出一種三元聯邦平均協議,減少聯邦學習系統中的上下游通信,該方案從保護物聯網設備的隱私和安全出發,在降低通信成本和提高學習性能方面取得一定成效。文獻[12]為滿足聯邦學習的環境需求,提出稀疏三元壓縮新的壓縮聯邦學習框架,解決了在聯邦學習訓練期間存在通信開銷量大的問題。
現有的聯邦學習框架假設各移動設備都無條件參與聯邦學習[13-14]。在訓練數據模型中,各移動設備都會產生相應的訓練成本,如果沒有激勵策略,自私的數據擁有者將不愿意參加聯邦學習[15-16]。此外,由于聯邦學習中任務發布者不知道參加模型訓練的數據擁有者的數據質量,以及可計算資源量,因此任務發布者和數據擁有者之間存在信息不對稱的情況。
為進一步考慮理性參與者的存在,文獻[17]提出一種參與者是理性參與方的理性證明系統,將博弈論中的理性用戶[18-21]引入到各安全協議中。文獻[22]研究了計算能力受限的理性參與者問題。
為解決聯邦學習的安全隱私與通信開銷問題,本文結合Micali-Rabin 隨機向量表示技術和博弈論框架,提出一種高效的聯邦學習方案。根據博弈論激勵機制,構建聯邦學習的博弈模型,其包括聯邦學習的各參與者、效用函數等擴展式博弈各要素。利用Micali-Rabin 隨機向量表示技術和Pedersen 承諾機制保障聯邦學習中各參與者訓練數據的安全與隱私,以達到全局帕累托最優狀態。
1 相關理論
1.1 博弈論
本文對博弈論中擴展式博弈和帕累托最優的基本概念進行簡單說明。
定義1(擴展式博弈)博弈論是一門用于數學模型研究理性決策者之間如何互動的學科,參與者之間的互動可能涉及到沖突,也可能涉及到合作。擴展式博弈是個六元 組(P,S,φ,ρ,U,E),包括以 下6 個要素:1)參與者集合P,表示參與聯邦學習的所有參與者集合,包括任務發布者和數據擁有者;2)參與者的行動策略集合S,指某個參與者在某個時間采取的某種行動策略的集合;3)外生隨機變量φ,不受任何參與方控制的隨機影響方案的變量參數;4)參與者的風險規避ρ,當每次方案執行時,各個理性參與者在聯邦學習方案中能夠承擔的各類風險規避程度;5)參與者的效用函數U,在采取某種行動策略結束后,每個參與者會獲得相應收益;6)參與者的期望效用E,表示達到帕累托最優狀態后,所有參與者達到最大化的期望效用。
定義2(帕累托最優)帕累托最優是將所有資源進行合理分配的一種理想狀態,當全局參與者模型達到帕累托最優狀態后,不會存在一方的效用利益變好,而另一方的效用收益就會因此而受到損失的情況。在這個狀態下,所有的理性參與方都會選擇合理的行動策略,使得自己的效用利益最大化,并且全局的效用也是最大化。
如果全局參與者模型達到帕累托最優狀態,那么就會滿足交換最優、生產最優和產品最優等條件。各個理性參與者在生產交易過程中,即使交換或更改生產條件或者環境,都不會從中再獲得利益,從而影響他人利益。各資源已達到理想狀態,不存在帕累托改進的狀態,即帕累托最優。
1.2 Pedersen 承諾機制
Pedersen 承諾機制是滿足無條件秘密性的同態承諾機制,構造承諾機制需要3 個階段:1)初始化階段,選擇任意乘法群Gq,其中q為大素數,群Gq的生成元為g、h,并公布(g,h,q);2)承諾階段,發送承諾方隨機選擇值r?Zq,并計算承諾值COM=gmhrmodq,其中m是需要加密的信息,然后將承諾值COM 發送給接收方;3)打開階段,發送方將(m,r)一同發送給接收方,接收方驗證承諾值COM 是否等于gmhrmodq,若是gmhrmodq,則接收,否則拒絕接收任何信息。
1.3 Micali-Rabin 隨機向量表示技術
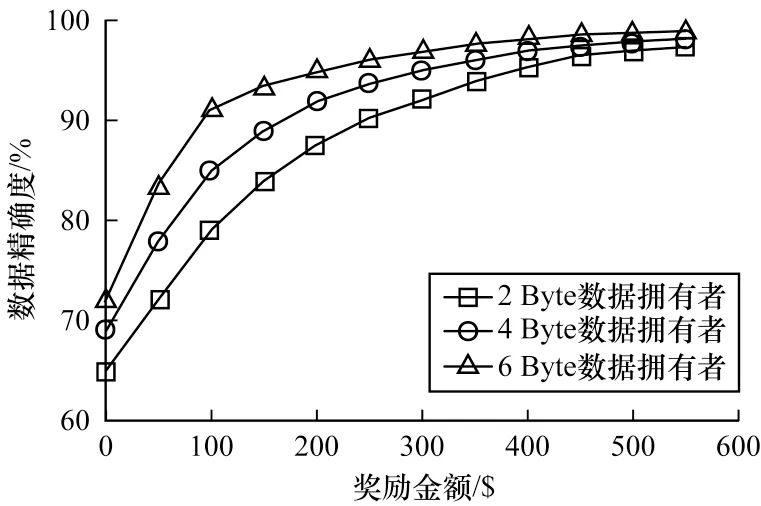
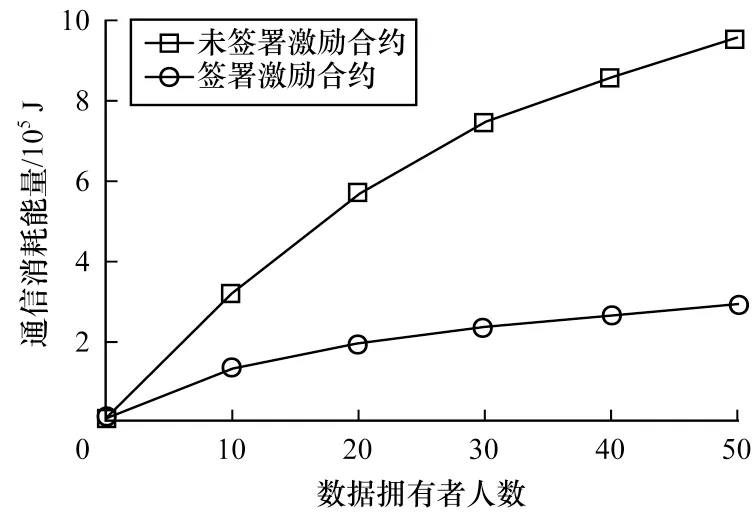
Micali-Rabin 隨機向量表示技術是基于Pedersen承諾,通過零知識證明技術證明方案中等式的正確性。假設Micali-Rabin 隨機向量表示技術存在有限域Fp,p為256 bit 的素數,g、h是群Gq的生成元,q為大素數,且q>p,具有以下3 個性質:1)設X的隨機向量表示是X=(u,v),其中u、v?Fp,X的值是val(X)=(u+v)modp;2)對隨機向量X=(u,v)的分量進行承諾,COM(X)=(COM(u),COM(v)),其中COM(u)=e(P,Q)u,COM(v)=e(P,Q)v,P、Q?G是 群G的兩個生成元;3)假設存在一行承諾值C OM(X1),COM(X2),…,COM(Xj),對于任 意i(1 ≤i 高效聯邦學習博弈模型是結合博弈論與聯邦學習,從聯邦學習參與方自利的角度出發,通過效用函數來保證聯邦學習數據的安全與隱私。為激勵具有高質量的數據擁有者積極參加聯邦學習,本文基于博弈論框架設計合理有效的激勵合約,將各理性參與者貢獻的資源映射到適當的貨幣獎勵中。參與者在追求自身利益最大化的同時滿足聯邦學習全局的利益最大化,從而達到帕累托最優狀態。本節設計的高效聯邦學習博弈模型包括七元組(P,φ,S,P(·),ρ,U,E)。 聯邦學習各個參與者集合P是聯邦學習中任務發布者和擁有若干能夠訓練模型的各個數據擁有者。外生隨機變量φ是指各個參與方無法預料與控制的外生隨機變量。策略集合S是聯邦學習中各個參與方有可能會采取的行動策略集合。支付函數P(·)是任務發布者激勵數據擁有者提供更高質量數據,以獲得支付報酬與獎勵。風險規避函數ρ是聯邦學習中所有參與者在模型訓練時所能承受的風險規避程度。期望效用函數U,Un:S→R(其中R為實數空間),表示第n位局中人在不同的行動策略組合下所獲得的期望收益效用函數。總期望效用函數E是在聯邦學習總的模型中,所有參與者達到的最大期望收益效用函數。 高效聯邦學習首先需要建模其方案中各個參與者,在博弈模型中主要存在兩類參與方,即聯邦學習任務的發布者Pi和數據擁有者Pj,并且兩類參與方都是理性自利的。任務的發布者在保證聯邦學習模型中全局利益最優的前提下,需要實現個體利益最優。數據擁有者在完成任務的前提下,實現個體利益的最大化。因此,在本文博弈模型中參與者集合為P=(Pi,Pj)。 在聯邦學習博弈模型中存在一些不受任何參與方控制的影響因素,本文將其稱為外生隨機變量φ,且φ是服從均值為0、方差為σ2的正態分布。聯邦學習中存在不確定外生因素的任務發布者與數據擁有者之間的博弈樹,如圖1 所示,其中變量s和d分別表示任務發布者和數據擁有者的收益。 圖1 任務發布者與數據擁有者之間博弈樹Fig.1 Game tree between task publisher and data owner 在高效的聯邦學習博弈模型中,由于所有參與者都是自利的,因此任務發布者在發布任務后可以選擇“激勵”或者“懲罰”數據擁有者。令si1表示選擇“激勵”策略,此時si1=1。而si2表示選擇“懲罰”對方的策略,此時si2=0。因此,任務發布者的行動策略集合為(激勵,懲罰),即si=(si1,si2)。 自私的數據擁有者在接收到任務后可以選擇“誠實”或者“惡意”策略進行訓練數據與反饋。令sj1表示選擇“誠實”執行任務策略,此時sj1=1,而sj2表示選擇“惡意”的策略,此時sj2=0。因此,數據擁有者的行動策略集合為(誠實,惡意),即sj=(sj1,sj2)。 當雙方都選擇利于自己的行為策略時,且雙方都能達到最大效用時,令π=ks+φ表示雙方達到最大效用時的貨幣表示形式,k(k≥0)表示參與方選擇不同行動策略時對雙方整體效用的影響系數。在執行任務過程中存在不受控制的環境變量φ,且φ服從正態分布,因此聯邦學習的雙方總期望效用函數為E(π)=E(ks+φ)=ks,var(π)=σ2。參與方采取的行為策略會影響全局中整體的效用均值。 在聯邦學習博弈模型中,任務發布者通過激勵數據擁有者訓練數據模型,從而獲得高質量數據。因此,本文將任務發布者給予數據擁有者的獎勵金額設置為線性函數,如式(1)所示: 其中:α為模型中數據擁有者進行訓練數據的固定收入金額;β為任務發布者給予數據擁有者的激勵獎金系數。針對式(1)中的固定收入金額和激勵獎金系數是根據博弈論中委托代理理論計算得到的,其中數據擁有者的獎勵金額是隨著激勵金額的增加而增加。在本文方案中,任務發布者和數據擁有者的風險規避函數ρ1和ρ2不會影響各自的收入水平,因此任務發布者給予數據擁有者的獎勵金額可以設置為線性函數。 在參與者學習的過程中,參與者將付出一定的努力使得自身的利益最大化,此時會產生相應的努力成本。本文用貨幣成本來衡量參與者的努力成本,當任務發布者采用不同的策略時,其努力成本如式(2)所示: 同理,數據擁有者采取不同策略時的努力成本如式(3)所示: 其中:x1和x2分別表示任務發布者和數據擁有者選擇不同行動策略時的努力成本系數,且x1>0,x2>0;η表示數據擁有者選擇不同的行動策略后取得相應的成效系數,并且0<η<1。數據擁有者越努力獲取高質量的數據,任務的發布者所獲得實際收益與預期收益之間的差距越小。 由于所有的參與者都是理性的,個體間會存在一定的差異性和特殊性,因此各個參與者之間對聯邦學習過程中的風險規避程度也會存在一定的差異。在博弈模型中,本文設計的風險規避效用函數為u=-eρω,其中ρ為參與者的絕對風險規避度量,ω為實際獲取的收益。由于參與者都具有風險規避的特性,因此會存在相應的風險成本。任務發布者承擔風險的成本如式(4)所示: 數據擁有者承擔風險的成本如式(5)所示: 其中:ρ1和ρ2分別表示任務發布者和數據擁有者的風險規避程度,且ρ1>0,ρ2>0。 在博弈模型下分析聯邦學習方案最關鍵的是定義參與者的效用函數。在本文方案中,由于參與者都是理性自利且具有風險規避特性,因此其效用函數需要通過參與者的實際收益進行建模。任務發布者的實際收益如式(6)所示: 數據擁有者的實際收益如式(7)所示: 根據參與者的實際收益與他們分別存在的風險成本,可以得到任務發布者的期望效用函數,如式(8)所示: 同理,數據擁有者的期望效用函數,如式(9)所示: 由于聯邦學習框架中的參與者都是理性自利的,因此數據擁有者選擇與任務發布者簽訂激勵合約后,得到的最大效益必須大于不簽署該合約。數據擁有者通過與任務發布者簽署激勵合約后的期望效用不得小于不接受該任務得到的最小保留效用此時數據擁有者需要考慮與自己相關的參與約束IR,如式(10)所示: 任務發布者不知道數據擁有者提供的數據質量,在雙方存在信息不對稱的情況下,并且理性的數據擁有者總會選擇使自己期望效用最大化的行為策略。因此,任務發布者希望得到的最大效用通過數據擁有者的最大效用來實現,且全局達到帕累托最優狀態。 根據任務發布者和數據擁有者簽署的激勵合約及帕累托最優狀態情況,只有當數據擁有者選擇行動策略sj時,其效用比其他行動策略sj′更大。因此,數據擁有者根據其理性行為將會選擇行動策略sj,使得自己的利益最大化,以及全局的利益最大化,此時有maxsj(w)。令可以得到在聯邦學習博弈模型中存在一個激勵相容約束IC,如式(11)所示: 將參與約束IR 和激勵相容約束IC 帶入任務發布者期望最大效用的目標函數中,構建拉格朗日函數,可得: 根據以上函數的變化趨勢可以看出,任務發布者的風險規避程度ρ1與其給予數據擁有者的激勵系數ρ呈正相關。因此,當雙方利益最大化時,數據擁有者所選擇的行動策略如式(15)所示: 在聯邦學習博弈模型中任務發布者和數據擁有者總的期望效用達到最大,如式(16)所示: 由此可以看出,在聯邦學習模型中,即使任務發布者不知道數據擁有者所選擇的行動策略和其努力程度,但是根據雙方簽署的激勵合約,數據擁有者會選擇最優的行動策略sj,使得雙方都達到最大的期望效用。此時聯邦學習模型的總期望效用E(π)也達到最大,即模型的全局達到帕累托最優狀態。 本文基于上述設計的聯邦學習博弈模型,結合Micali-Rabin 隨機向量表示技術構造高效安全的聯邦學習方案。在本文方案中,各參與者為了使自身利益最大化必須遵循雙方簽署的激勵合約,通過各自的效用函數約束個人理性行為,任何偏離合約的一方都會受到遠大于自身成本價值及影響自身聲譽的懲罰。 任務發布者Pi公布需要訓練學習的初始模型任務T,并將其送至中央服務器,同時與滿足條件的各數據擁有者Pj簽署激勵合約,建立安全的連接。任務發布者和數據擁有者為保證數據的安全與隱私,根據橢圓曲線的密碼體制隨機選取密鑰對,用于雙方在方案中交易的驗證。本文方案選擇一條安全的橢圓曲線E,其中G為該橢圓曲線的一個基點,基點G的階數為n。本文選擇隨機數λ計算d=λG,其中d為公鑰,隨機數λ為私鑰,并公開(G,d)。 各數據擁有者Pj從中央服務器下載公布的初始模型參數θi。每個數據擁有者利用自己的本地數據選擇行動策略sj,并訓練初始化模型,之后將更新后的參數返回至中央服務器,使得自身利益最大化。在此過程中,數據擁有者對已更新的參數進行3k行承諾以便于追溯與認定惡意數據擁有者返回的無用數據。形成的3k行承諾采用Micali-Rabin 隨機向量表示技術可以表示為: 在這個階段中要求任意概率多項式時間的接收方都不能獲取有關承諾的任何信息,以保護所有數據的隱私和安全,。 任務發布者Pi與各數據擁有者Pj進行交互式證明后,若通過承諾值的驗證,任務發布者將接收更新的參數此時Pi通過各參與者得到期望效用函數,并對各自在聯邦學習中的收益成效進行判斷,雙方是否選擇最優的行動策略來執行方案。若任意一方參與者的效用值未達到最大偏離方案,根據激勵合約的規定,需要支付對方遠大于自己期望效用Ui或者Uj的賠償金作為未遵守方案的補償。 當任務發布者Pi確定接收更新的參數后,中央服務器根據各參與方更新參數的聚合結果,并對全局模型的參數進行更新。更新后的參數被重新發送至各數據擁有者Pj,各數據擁有者Pj重新利用自己的本地數據進行訓練模型,重復本地訓練階段,直到全局模型的各項性能指標滿足任務發布者的要求后,聯邦學習階段結束。 由于構造的方案中各方參與者都是理性自利的,他們會為了使自身利益得到最大化選擇最優的行動策略。在該方案中,根據雙方簽署的激勵合約,一旦有參與者選擇偏離方案的惡意行為,將會受到嚴重的資金懲罰。各參與方通過激勵合約約束并激勵自己遵守方案,降低各參與方通信的風險,并提高聯邦學習的通信效率。高效聯邦學習系統架構如圖2 所示。 圖2 高效聯邦學習系統架構Fig.2 Architecture of efficient federated learning system 本文從安全性分析基于博弈論優化的高效聯邦學習方案。 定理1本文聯邦學習方案具有安全性。 證明在聯邦學習的本地訓練階段中,各數據擁有者采用Micali-Rabin 隨機向量表示技術對承諾值1 ≤l≤3k進行3k行承諾。在聚合驗證階段中,任務發布者Pi與各數據擁有者Pj進行交互式證明,以驗證承諾值的正確性。各數據擁有者在安全通道中向任務發布者打開承諾分量以保證更新參數的安全性與隱私性。 本文從正確性分析基于博弈論優化的高效聯邦學習方案。 定理2本文聯邦學習方案具有正確性。 證明本文聯邦學習方案中,如果任務發布者Pi與各數據擁有者Pj嚴格按照合約進行執行,那么雙方都會選擇最優的行動策略執行方案。在方案的初始化階段,任務發布者和滿足條件的數據擁有者簽署激勵合約,以建立安全的連接。在本地訓練和聚合驗證階段,數據擁有者將更新的參數和承諾值返回至中央服務器。若數據擁有者選擇行動策略sj2,即“惡意”的行動策略,那么得到的效用收益為因為策略sj2的取值為0,所以由式(9)可以將其效用收益化簡寫為對應任務發布者的效用收益為當參與方達到最大收益時π′=ksj2+φ=φ,且φ服從正態分布,因此,本文方案的雙方總期望效用為E(π)=E(ksj2+φ)=ksj2=0,無法達到帕累托最優狀態。根據激勵合約的規定,選擇行動策略sj2的參與方將受到嚴重的懲罰。 由于雙方都是理性的,在方案中為了自身利益最大化不會選擇不利于自己的行動策略,只有雙方都選擇最優策略,全局才能達到最優狀態πmax=ks+φ,且參與者都能獲得最優收益,全局達到帕累托最優狀態。因此,該高效聯邦學習方案是正確的。 本文從公平性分析基于博弈論優化的高效聯邦學習方案。 定理3本文聯邦學習方案具有公平性。 證明在高效聯邦學習方案中,所有參與者都是理性自私的,為了自身利益的最大化可以隨意選擇自己的行動策略。為保證本文方案的公平性,在方案的初始化階段中,任務發布者需要與數據擁有者簽署激勵合約,嚴格按照合約的要求執行。 雙方選擇的策略在激勵合約中的取值為“0”或“1”。一種情況是雙方根據自己的效用函數Ui和Uj判斷雙方是否存在偏離方案的惡意行為,如果有惡意行為,它們總的期望效用E(π)=E(ks+φ)的結果為“0”。根據策略s可以找出惡意參與者,并對其進行懲罰。另一種情況是根據上傳至中央服務器的承諾值判斷是否存在惡意參與者,根據方案的安全性分析可知,任何參與者都無法更改或者虛假地更新參數,因此,本文方案對于所有參與者都是公平的。 不同方案的安全性、正確性和公平性對比如表1所示,其中,“√”表示方案滿足上述性質,“×”表示方案不滿足上述性質。 表1 不同方案的性能對比Table 1 Performances comparison among different schemes 從表1 可以看出,現有的大多數聯邦學習方案考慮方案的安全性,但是通常認為參與者都是誠實的,未考慮到參與者的自利行為,即對方案的公平性方面考慮的較少,這也是影響聯邦學習效率與應用的原因之一。 本文借鑒文獻[24]的數字分類數據集MINIST對本文方案進行模擬評估。本文選擇60 000 條訓練數據示例,其中包含1 個任務發布者和50 個數據擁有者,用于執行數據訓練分類任務。數據擁有者首先與可以接受模型訓練的數據擁有者簽訂激勵合約。簽訂合約的數據擁有者根據任務發布者上傳的任務,隨機分配需要訓練的數據集,并作為本地的訓練數據。 為驗證激勵合約的有效性,本文分別對簽署和未簽署激勵合約的參與者進行聯邦學習,并對擁有不同數據字節長度的擁有者利益和任務發布者的利益關系進行分析討論。簽署與未簽署激勵合約的總期望效用對比如圖3 所示。從圖3 可以看出,當擁有者的數據字節長度分別為2、4 和6 Byte 時,無論數據類型為何種的數據擁有者,他們與任務發布者之間的效用只有當都選擇簽署激勵合約時,雙方的效用才最大,此時方案全局的利益也最大,即達到帕累托最優狀態。 圖3 簽署與未簽署激勵合約的總期望效用對比Fig.3 Total expected utility comparison of signed and unsigned incentive contracts 本文對任務發布者和數據擁有者的激勵策略進行分析,確定任務發布者給予的激勵金額大小與數據訓練精確度之間的關系。數據的精確度隨獎勵金額的變化趨勢如圖4 所示。隨著任務發布者提供的激勵獎勵的增加,擁有不同數據類型數據擁有者的數據訓練精確度從65%逐步提高至98%。在本文激勵合約下,當任務發布者的激勵獎勵越高時,越能激勵數據擁有者進行模型訓練,最終獲得的數據質量也越高,從而實現高效的聯邦學習。 圖4 不同獎勵金額下數據的精確度Fig.4 Accuracy of data under different reward amounts 簽署與未簽署激勵合約擁有者的通信消耗能量對比如圖5 所示。當未簽署與簽署激勵合約的數據擁有者從0~50 逐漸增加時,其通信開銷發生了很大的變化。從圖5 可以看出:當參與者未簽署激勵合約時,其數據擁有者越多,通信開銷越大;有激勵合約的參與者通信開銷幾乎無變化,驗證了本文聯邦學習方案的高效性。 圖5 簽署與未簽署激勵合約擁有者的通信消耗能量對比Fig.5 Energy consumption of communication comparison of owner with and without incentive contracts 本文方案性能的影響因素是參與者的自利性行為。若參與者是自私惡意的,在方案執行過程中,由雙方的激勵合約可知,雙方將根據效用函數對自私惡意的參與者進行懲罰,并且阻止方案繼續執行。不同參與者行為聯邦學習效率變化如圖6所示。當擁有不同數據類型的參與者若存在自私惡意的數據擁有者,方案的效率將降低。 圖6 不同參與者的聯邦學習效率對比Fig.6 Efficiency of federated learning comparison among different participants 本文設計的方案中用戶的獎勵越大,其選擇積極策略的可能性越大,獲得的數據準確度也越高,用戶的通信消耗量遠遠小于用戶未簽署激勵合約的通信量。當擁有不同數據類型的參與者存在理性惡意的數據擁有者時,極大影響聯邦學習的效率,從而影響雙方效用收益。因此,本文設計的方案是有效的。 本文提出基于博弈論優化的高效聯邦學習方案,利用博弈論激勵高質量的數據擁有者和任務發布者,同時結合Micali-Rabin 隨機向量表示技術和Pedersen 承諾方案,實現高效聯邦學習的隱私保護。仿真結果表明,該方案不僅使得全局參與者達到帕累托最優狀態,而且為聯邦學習的各參與者的利益和數據隱私提供了保證。后續將在多任務者同時發布模型訓練任務的前提下,從不同的角度和應用場景中研究聯邦學習,進一步提高學習效率。2 聯邦學習博弈模型
2.1 參與者集合
2.2 外生隨機變量
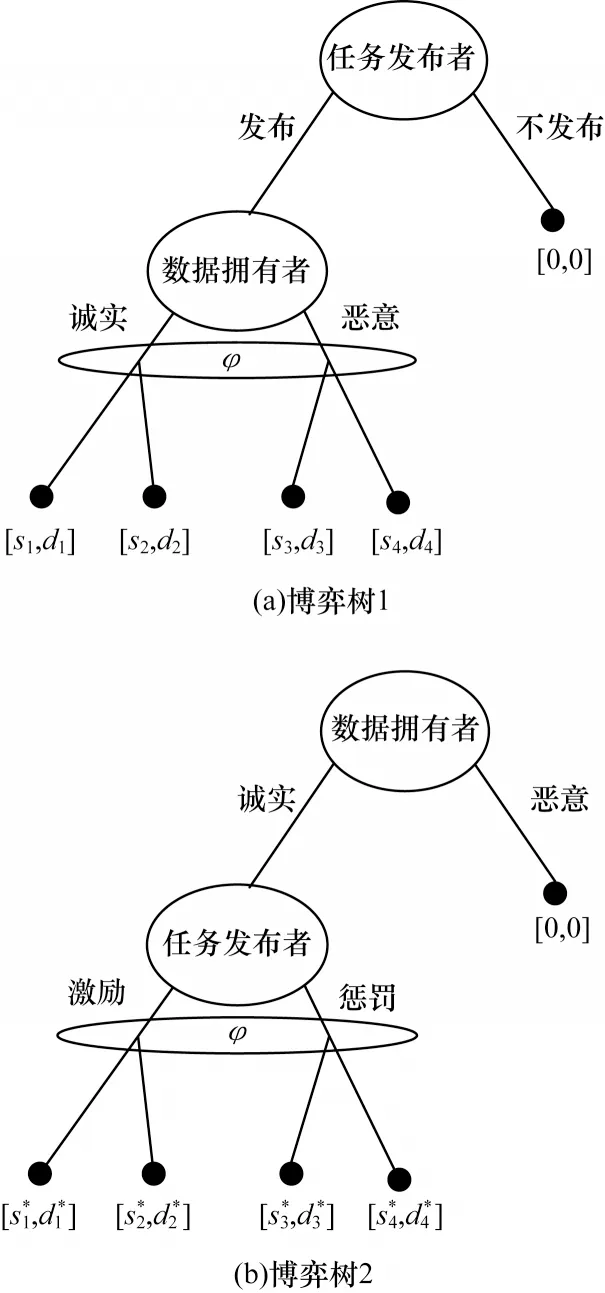
2.3 策略集合
2.4 支付函數



2.5 風險規避


2.6 期望效用函數


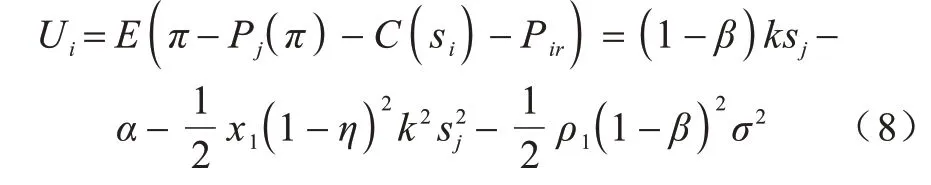

2.7 總期望效用


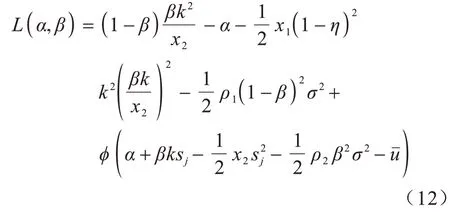

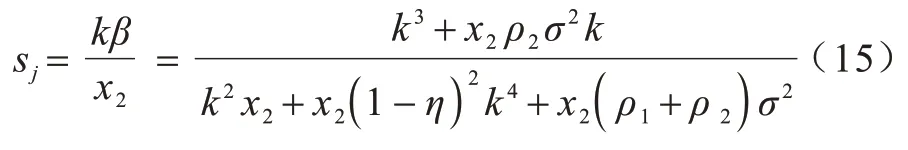

3 高效聯邦學習方案
3.1 初始化階段
3.2 本地訓練階段
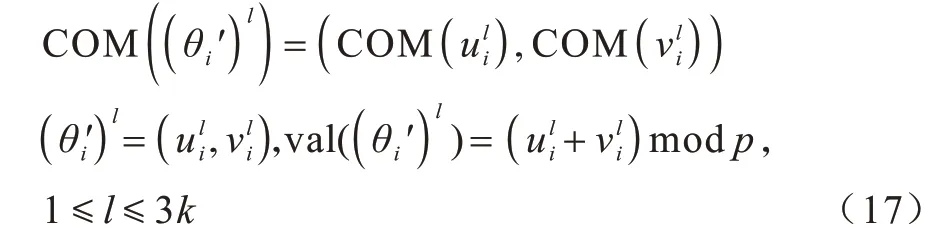
3.3 聚合驗證階段

3.4 模型更新階段

4 方案分析
4.1 安全性分析

4.2 正確性分析
4.3 公平性分析
4.4 方案性能分析

5 實驗仿真


6 結束語

