時變腐蝕電流密度下預應力混凝土梁可靠度分析
周孝飛,羅進鋒,王 磊
(1.湖南省交通科學研究院有限公司 長沙市 410000; 2.湖南湘科建設工程檢測有限責任公司 永州市 425000)
0 引言
通電加速銹蝕試驗可以模擬鋼筋的銹蝕,因而可以較好地分析混凝土結構性能退化過程[1]。鋼筋銹蝕是基于腐蝕電流密度等因素的電化學過程,因而利用腐蝕電流密度可以較好地分析混凝土結構中鋼筋的銹蝕起始時間及銹蝕率[2]。目前,隨著預應力混凝土結構的廣泛使用,由鋼筋銹蝕引發的安全問題已成為混凝土結構工程師面臨的嚴峻問題[3]。因此,有學者開始展開了腐蝕電流密度對預應力混凝土結構抗力衰退的影響。沈銳利等[4]利用可靠度理論分析腐蝕狀態下懸索橋預應力錨固系統的可靠度,發現腐蝕電流密度的增加容易導致錨固系統可靠度降低,且腐蝕密度為0.15μA/cm2是評判錨固系統滿足目標可靠度指標的依據。樊玲等[5]采用恒電流線性極化法測量鋼筋銹蝕電流密度規律,發現腐蝕電流密度的變化除了與時間相關外,還與不同深度處的氯離子濃度相關。此外,預應力筋與混凝土能良好的協同工作,主要是有良好的粘結性能[6]。上述研究得到了一些成果,然而腐蝕電流密度大于1μA/cm2后,在設計基準期內,鋼筋的剩余面積會趨向于0,這與實際情況不符[3]。實際的預應力混凝土結構需考慮粘結強度、氯離子濃度對腐蝕電流密度的影響,還需考慮腐蝕電流密度的時變性。因此,為了再現預應力混凝土結構在腐蝕電流密度下的抗力性能退化的真實情況。首先建立了粘結強度-氯離子濃度的時變腐蝕電流密度模型,隨后以實例中的橋梁為例,開展了預應力結構抗力計算,預測該箱梁橋腐蝕開始后100年內的失效概率,并開展了腐蝕電流密度和混凝土抗壓強度時變效應的敏感性分析。
1 模型分析
1.1 腐蝕開始時間
預應力混凝土梁在受到預應力作用下,氯離子擴散進程會受到影響。因此,引入應力影響系數f(σ)[7]可以分析預應力對氯離子擴散性能的影響。
Dσ=f(σ)D0
(1)
式中:Dσ為應力σ狀態下的氯離子擴散系數;D0為無應力狀態下的氯離子擴散系數。
式(1)中,當預應力筋處于張拉狀態,混凝土會受到拉應力作用,系數f(σ)=1-0.0125σ+0.2082σ2。使用Fick第二擴散定律模擬氯離子在混凝土中的擴散效應,預應力筋表面的腐蝕開始時間[8]用式(2)進行描述:
(2)
式中:C為保護層厚度;er(·)為誤差函數;C0為混凝土表面氯離子濃度;Ccr為氯離子臨界濃度;m為復雜系數,與混凝土材料性質有關[7]。
1.2 預應力筋腐蝕剩余面積及腐蝕電流密度
當時間達到Ti后,預應力筋與氯離子發生電化學反應,造成鈍化膜破壞,引起預應力筋的腐蝕。假設預應力筋的表面在腐蝕作用下各部分腐蝕量相同,在腐蝕電流密度icorr和時間t下,剩余面積Ast(t)[9]為:
Ast(t)=3πr2+4π[r-0.0116icorr(t-Ti)]2,Ti≤t
(3)
實際工程應用中,腐蝕電流密度除與時間相關外,還與粘結強度因子相關。在設計基準期內,一般用粘結強度因子描述粘結強度對腐蝕電流密度的影響[2]。通過對文獻[6]的調研可以看出,粘結強度因子與時變腐蝕電流密度利用線形分布關系更加符合工程實際,即式(4)所描述的。
icorr(t,δ)=icorr(t)·δ
(4)
式中:icorr(t,δ)為考慮時變和粘結強度的腐蝕電流密度;icorr(t)為考慮時變效應的腐蝕電流密度;δ為粘結強度因子。對于鋼筋銹蝕下腐蝕電流密度的變化情況,房久鑫[10]開展了鋼筋混凝土構件的耐久性加速模擬試驗,試驗周期為1200d,并得出腐蝕電流密度隨時間的變化關系曲線。然而,該關系曲線在分析6年之后的腐蝕電流密度后,腐蝕電流密度達到1.3μA/cm2,且數值緩慢減小,這與實際情況不符。樊玲等[5]研究了不同濃度NaCl溶液對鋼筋混凝土的銹蝕影響,得到了不同濃度下腐蝕電流變化規律,基于樊玲的數據及公式,得到如下公式:
icorr(δ,t)=δ·α(12.419CCl-+2.055)(1-eγt)
(5)
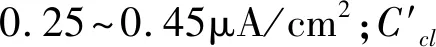
對于粘結強度因子,Lin等推導出了粘結強度與腐蝕電流密度之間的關系式,并用粘結強度因子進行表示。
(6)
式中:k3為經驗參數。在設計基準期內,腐蝕電流密度隨時間的增長會有增加,但在服役20年左右,腐蝕電流密度的增速逐漸減緩[3]。實際工程中,腐蝕電流密度一般都較小[11],在設計基準期內不太可能達到200μA/cm2,因此,粘結強度因子取1較為合適。
1.3 結構可靠度
由可靠度定義及規范[12]可知,隨時間變化的可靠度評估極限狀態方程[8]用公式(7)表示為:
Z(t)=R(t)-SG-SQ(t)
(7)
式中:R(t)為結構自身抗力的彎矩;SG和SQ(t)分別為恒載和活載所產生的彎矩;Z(t)為結構功能函數。
考慮到混凝土材料性質和預應力筋面積等參數都具有時變性,且各參數的分布類型不一致[13],計算橋梁失效概率較為復雜。因此,本研究采用Monte Carlo方法進行計算求解箱梁跨中截面抗彎承載能力失效概率。對隨機變量進行了107次隨機抽樣。
2 實例分析
2.1 實例參數[13]
一座70m+115m+60m三跨預應力混凝土連續剛構箱梁橋。取主跨的跨中截面實例參數進行抗彎承載力進行計算分析。利用Midas軟件建立橋梁的三維模型,見圖1。
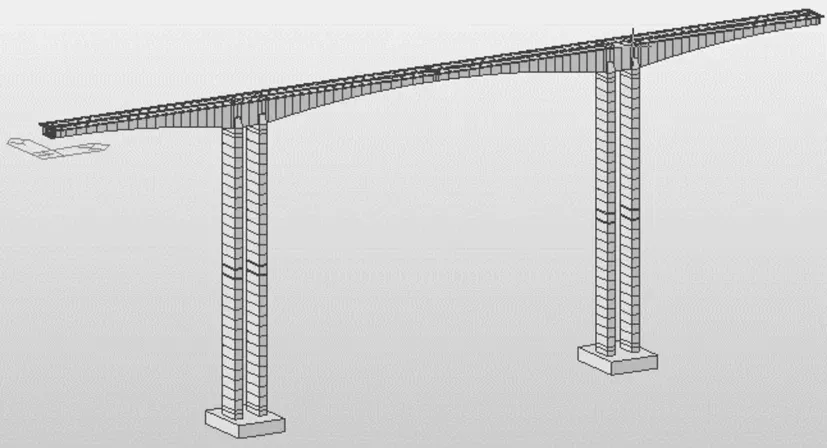
圖1 Midas三維模型
橋址所處的環境會有氯鹽殘留在梁體表面。將箱型截面等效換算為工字形梁截面,工字形截面中有效寬度為8359mm,有效高度為2540mm,恒載和車輛荷載效應等參數的具體數值見表1。
結合公式和實例參數,經分析和推導,該橋隨時間變化的可靠度評估的極限狀態方程見式(8)。
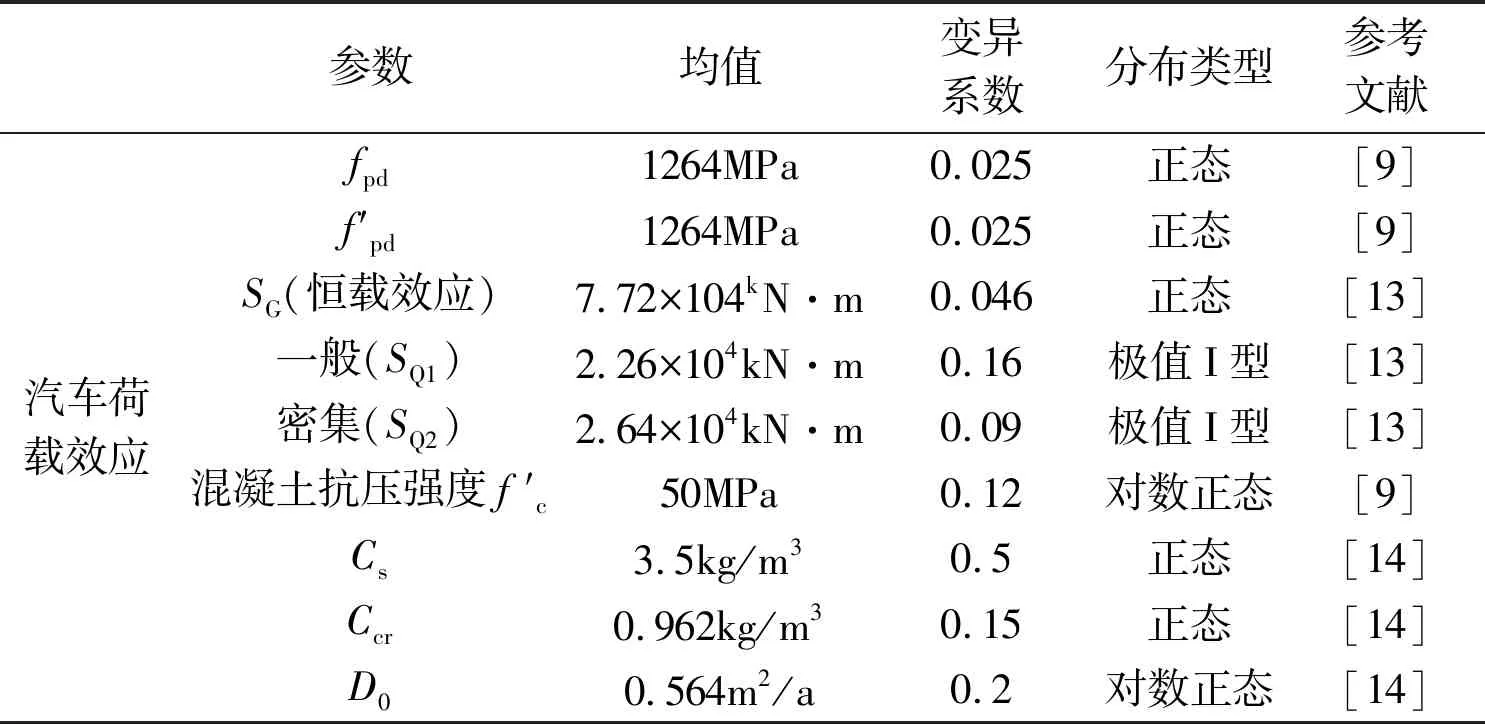
表1 參數統計表
(8)
式中:Ap(t)和Ap′(t)分別為受拉區和受壓區的預應力筋在t時的剩余面積;fcd(t)為隨時間變化的混凝土抗壓強度,用公式(9)表示[15]。
(9)
式中:α1、α2和α3都為混凝土抗壓強度退化影響參數。式(6)和式(9)中涉及的參數如表2所示。

表2 相關參數的具體數值[3,15]
2.2 結果分析
依據表1和表2給出的具體參數及圖1,結合式(1)~式(9),采用蒙特卡洛模擬方法,計算了箱梁跨中的失效概率。時變腐蝕電流密度對橋梁可靠度的影響如圖2所示,其中保護層厚度及其他條件相同。圖2中選取了時不變的0.25μA/cm2和0.45μA/cm2與時變腐蝕電流密度進行對比分析。從圖2中可以看出,隨著預應力混凝土結構使用時間的增長,該橋時變腐蝕電流密度的失效概率大于腐蝕電流密度為0.25μA/cm2和0.45μA/cm2的失效概率,且在服役100年后,時變腐蝕電流密度的年度失效概率為0.08,而0.25μA/cm2和0.45μA/cm2的年度失效概率分別為3.29×10-4和0.009。雖然0.45μA/cm2的腐蝕電流密度對預應力混凝土橋的腐蝕失效概率影響較大,但考慮時變腐蝕電流密度對該橋的腐蝕失效概率的影響更大,從圖2(b)中也可以找到同樣的規律。綜上表明:考慮腐蝕電流密度的時變效應是評估結構耐久性必須考慮的一個重要因素。
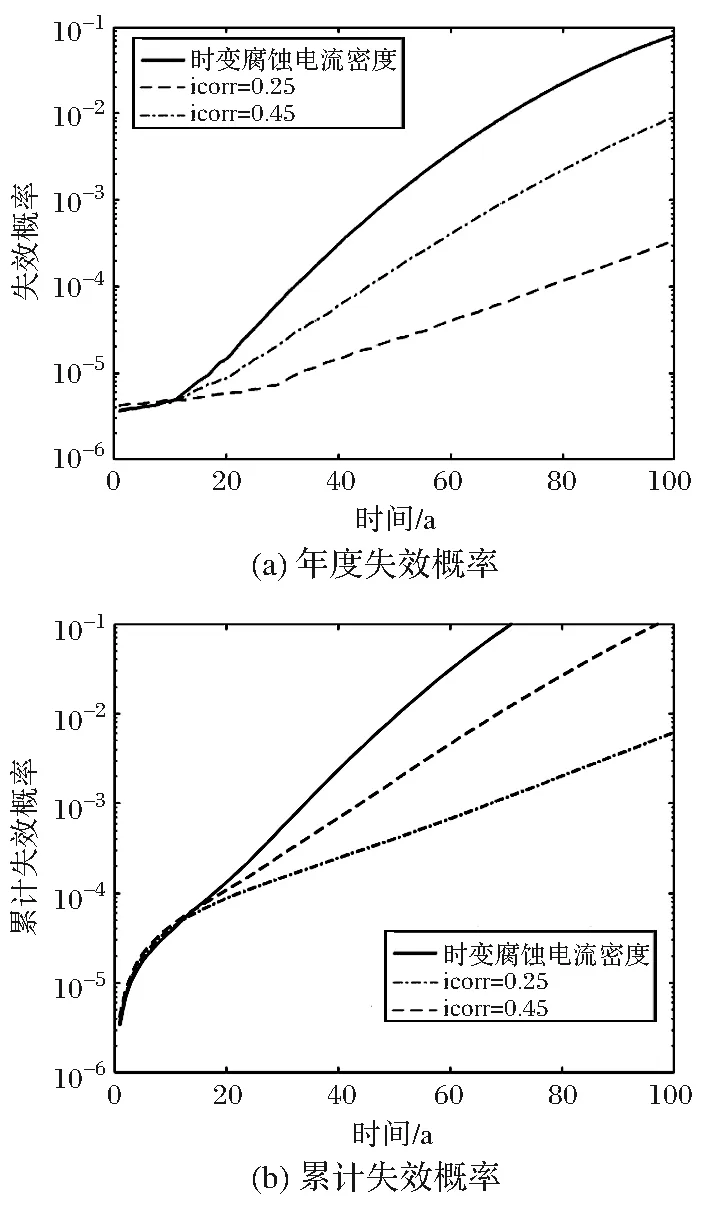
圖2 時變腐蝕電流密度
除了腐蝕電流密度具有時變性外,混凝土抗壓強度在服役過程中也隨時間的延長而降低[4]。因此,本研究分析混凝土強度和腐蝕電流密度的時變性對橋梁可靠度的影響,見圖3。從圖3中可以看出,當服役60年后,考慮混凝土強度和腐蝕電流密度時變性的年度失效概率達到0.01,而考慮腐蝕電流密度時變性的年度失效概率要達到0.01至少是服役65年后。從圖3(b)中可以看出,在服役年限為60年,考慮混凝土強度和腐蝕電流密度時變性的累計失效概率是0.180,考慮腐蝕電流密度的累計失效概率是0.035,即考慮混凝土強度和腐蝕電流密度時變性的累計失效概率是考慮腐蝕電流密度的5.1倍左右。綜上表明,混凝土強度隨時間的變化對于主梁的腐蝕失效有影響。在合理范圍內,讓混凝土強度不隨時間降低可以減緩失效概率的開始。
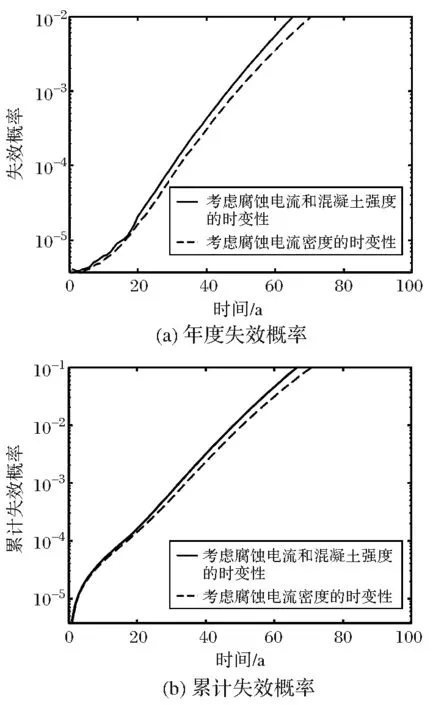
圖3 混凝土強度和腐蝕電流密度的時變效應
3 結論
考慮氯離子及粘結強度影響下的時變腐蝕電流密度,結合實橋的具體情況,本研究建立了MIDAS三維模型,考慮了幾個因素對主梁失效概率的影響。預測了100年內結構的失效概率。通過數據對比,可以得出以下結論:
(1)在設計基準期內,進行結構失效計算時,應當考慮腐蝕電流密度的時變效應。高腐蝕電流密度對結構的可靠概率降低有直接影響,但時變腐蝕電流密度更容易引發失效概率的增長。為確保結構的安全服役,應定期控制腐蝕電流密度數值的增長,使腐蝕電流密度盡可能的降低。
(2)當同時考慮混凝土強度和腐蝕電流密度的時變效應,結構的失效概率在服役60年后增加較快,極大影響結構的安全性,因此,在施工設計中要確保混凝土材料不隨時間發生劣化。

