連拱隧道掌子面縱向間距數值分析

■高 帥 胡明香 胡發旺

（1.江西省贛南公路勘察設計院有限公司，贛州 341000；2.贛州水務股份有限公司，贛州 341000）

近年來，我國交通基礎設施建設規模不斷擴大，交通運輸業實現高質量快速發展。 據統計，2021 年中國交通基建投資規模達3.6 萬億元， 總體朝著建設交通強國的目標大步邁進。 越嶺公路隧道作為山區公路的重要構造物，在改善公路線型、節省用地和節約投資等方面發揮著重要作用。 連拱隧道作為一種特殊的隧道形式，因其線形流暢、占地面積小、避免了洞口路基或大橋分幅、 經濟環保等優點，在雙洞雙向行車的公路短隧道建設中得到了廣泛應用。截至2020 年，我國公路隧道總數量突破2 萬座，總里程突破2 萬km，其中連拱隧道數量超過1600座，總里程達500 km 以上。 同時，連拱隧道已不限于公路山嶺隧道，在不同地理環境下，出現了隧道入湖、下海、過江、上島等更加廣泛的發展和應用趨勢[1]。交通建設實踐已證明，修建連拱隧道符合生態環境保護和綠色可持續發展的理念，也符合我國人多地少的基本國情。

不同于普通單線隧道或分離式隧道，連拱隧道由于開挖跨度大、施工工序交錯多、施工工藝復雜、圍巖應力變化和襯砌荷載轉換復雜等因素[2]，導致其施工難度大，安全隱患增多。 連拱隧道左右線施工開挖相互影響，在影響范圍內圍巖應力和變形互相疊加，先后行洞掌子面縱向間距大小影響兩者的疊加程度。 連拱隧道開挖施工時，為了減小左右洞的相互影響，先后行洞掌子面應保持合理的縱向間距，這樣不僅可以降低圍巖擾動，最大程度保證圍巖穩定，還能夠縮短工期，節約工程成本。 因此，對連拱隧道掌子面縱向間距分析具有重要的理論研究和工程實踐意義。

1 研究背景

目前對于隧道掌子面縱向合理間距的研究，多集中在雙線小凈距隧道方面。Chung[3]通過建立三維模型研究雙隧道相互作用效應，得出隧道影響周范圍內側向應力顯著增加的結論。Ng C W 等[4]通過對平行開挖雙線隧道荷載傳遞機制和先后行洞縱向間距變化對隧道穩定性影響的研究， 提出2.5 倍洞徑為雙線隧道縱向間距的臨界值。 杜菊紅[5]研究了小間距隧道不同掌子面間距對圍巖變形和應力產生不同的影響，提出掌子面最優間距為20 m 左右。袁飛等[6]以黃土連拱隧道為研究對象，通過對黃土連拱隧道動態施工的三維數值模擬，確定偏壓黃土連拱隧道施工過程中左右主洞掌子面的合理縱向間距為3 倍單洞跨度。 吳賁等[7]以韓府山小凈距隧道為研究背景，通過數值模型分析，認為掌子面距離控制在2 倍洞徑較為合理。楊子奇等[8]以九龍山—大郊亭區間隧道為研究背景，利用數值模擬軟件對相同隧道間距情況下不同掌子面距離對地表沉降造成的影響進行分析，提出最佳隧道施工掌子面距離為1～2 倍隧道洞徑。 厲廣廣[9]選取不同縱向間距同向開挖隧道模型作為研究對象，研究縱向間距變化對圍巖變形的影響程度，得出V 類圍巖臺階法施工雙線隧道合理縱向間距為1.5 倍及以上開挖洞徑。徐才厚等[10]以廣州地鐵工程案例為背景，采用有限元軟件對7 種不同縱向間距下的盾構隧道進行開挖模擬，提出縱向距離9 環為最佳縱向施工間距。

從掌子面縱向間距研究現狀來看，目前國內外針對連拱隧道的研究還相對較少，主要研究內容及成果多以小凈距雙線隧道為主。 本文以連拱隧道為研究對象，采用三維有限元數分析軟件Plaxis，對V 級圍巖三層復合曲中墻連拱隧道開挖施工進行數值模擬，分析不同縱向間距開挖條件下圍巖變形與應力特征，確定連拱隧道施工中左右主洞掌子面合理縱向間距大小。

2 數值模型建立

以廣東某連拱隧道為研究對象，該隧道形式為三層復合曲中墻連拱隧道。 隧道洞頂埋深為20 m，開挖高度為8.5 m，單洞寬度為10 m，隧道圍巖等級為Ⅴ級，隧道數值分析計算參數如表1 所示。

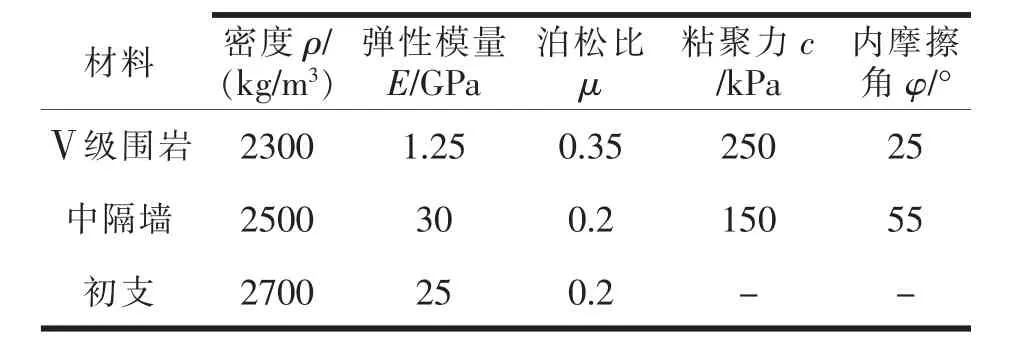
表1 數值分析計算參數

圖1 為連拱隧道三維數值計算模型示意圖，假設隧道圍巖為各向同性均質彈塑性介質，其屈服準則采用Mohr-Coulomb 準則。 不考慮構造應力和二次襯砌的影響，初期支護采用板單元模擬，采用提高噴射混凝土厚度來等效鋼拱架作用，初支模擬厚度取0.5 m。

圖1 連拱隧道三維數值計算模型

隧道施工采用中導洞施工法， 右洞為先行洞，總進尺長度為80 m， 右洞掌子面位置保持不變，調整左洞掌子面位置， 選取0D、0.5D、1D、1.5D、2D、2.5D、3D、3.5D、4D、4.5D、5D、5.5D、6D（D 為隧道單洞寬度）共13 個不同掌子面縱向間距進行數值模擬。為減小邊界約束效應的影響， 左洞取20 m 隧道進尺作為初始狀態。 表2 為不同掌子面縱向間距對應的隧道進尺長度， 圖2 為掌子面縱向間距為6D 時對應的連拱隧道開挖平面示意圖。

表2 不同縱向間距開挖情況

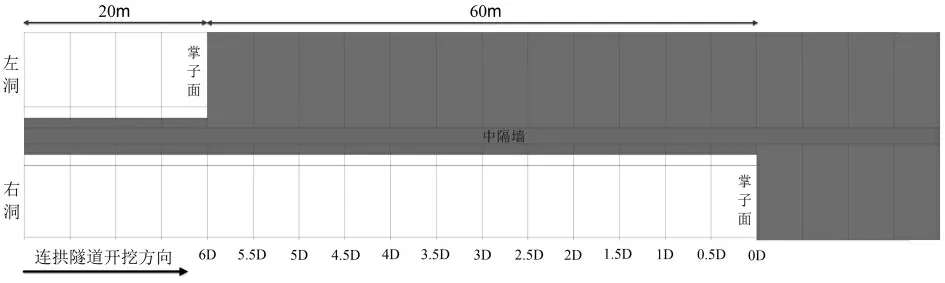
圖2 隧道開挖平面示意圖

3 計算結果分析

3.1 地表沉降分析

取右洞掌子面位置對應的橫斷面為特征斷面A，研究分析不同縱向間距條件下特征斷面A 所在地表沉降量，繪制地表沉降曲線，如圖3 所示。 圖中各曲線近似正態分布，且對稱中心隨著縱向間距的減小逐漸向中隔墻軸線位置偏移，表明掌子面縱向間距愈小，左右洞之間相互影響愈明顯。 此外，隨著縱向間距的減小，地表沉降量逐漸增大，縱向間距從6D 向2.5D 變化時，地表沉降量增速不明顯，但從2.5D 開始，地表沉降量增速顯著，沉降量大幅增加，并在0D 時于中隔墻處達到最大沉降量。因此，從地表沉降角度分析時，為降低左右洞開挖相互影響程度，掌子面縱向間距宜保持在2.5 倍及以上單洞寬度。

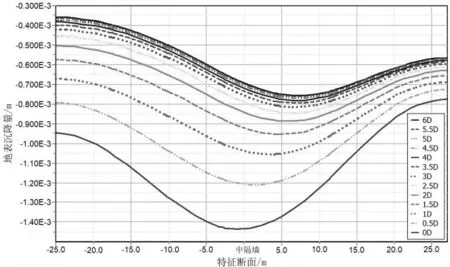
圖3 特征斷面A 地表沉降曲線

取中隔墻軸線方向豎直斷面為特征斷面B，圖4為不同縱向間距條件下特征斷面B 所在地表沉降曲線。 對比不同縱向間距對應的沉降曲線可以發現如下規律：隨著縱向間距的減小，沉降曲線線型由上凸曲線逐漸向上凹曲線過渡， 其中過渡曲線為2.5D 間距對應的沉降曲線， 同樣表明縱向間距越小，地表沉降越顯著，為降低隧道開挖對地表下沉的影響， 掌子面縱向間距宜保持在2.5 倍及以上單洞寬度。

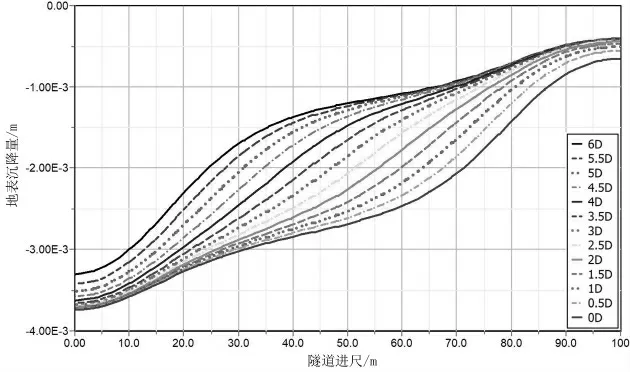
圖4 特征斷面B 地表沉降曲線

3.2 洞周收斂變形與應力分析

以右洞掌子面為研究對象， 分析不同縱向間距條件下對應的洞周收斂變形及應力大小。 圖5（a）為右洞掌子面處拱頂沉降變形隨縱向間距變化曲線，其線形為拋物線形，拱頂沉降變形隨掌子面縱向間距減小而逐漸增大， 取2.5D 作為拐點，2.5D 之前增長速率較小，2.5D 之后增長速率逐漸增快，表明為使相鄰左洞對右洞拱頂沉降的影響最小，兩洞掌子面縱向間距宜保持在2.5D 以上。 圖5（b）為右洞掌子面處拱底隆起變形隨縱向間距變化曲線，其線形與拱頂沉降變形曲線類似，拱底隆起變形隨掌子面縱向間距減小而逐漸減小， 取2.5D作為拐點，2.5D 之前減小速率不大，2.5D 后減小速率增大并趨于定值，因此為確保相鄰左洞對右洞拱底擾動最小，兩洞掌子面縱向間距宜保持在2.5D以上。

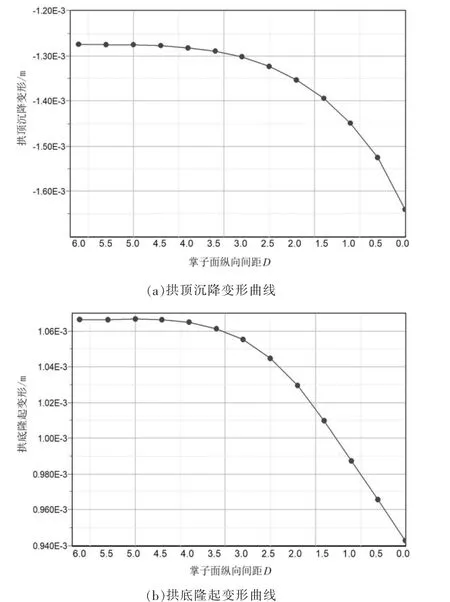
圖5 洞周收斂變形曲線

圖6（a）為右洞掌子面處拱頂總應力隨縱向間距變化曲線，通過觀察，縱向間距以2.5D 為拐點，在2.5D 之前拱頂總應力值幾乎不變，2.5D 之后拱頂總應力值逐漸遞增，故為減小相鄰左洞疊加在右洞拱頂的總應力， 兩洞掌子面縱向間距宜保持在2.5D 以上。 圖6（b）為右洞墻腰總應力隨縱向間距變化曲線，其線形為拋物線形，墻腰總應力隨著縱向間距減小而增加，同樣以2.5D 為拐點，2.5D 之前總應力增長速率緩慢，2.5D 以后增長速率逐漸增大， 因此為減小相鄰左洞疊加在右洞墻腰的總應力，掌子面縱向間距宜保持在2.5D 以上。

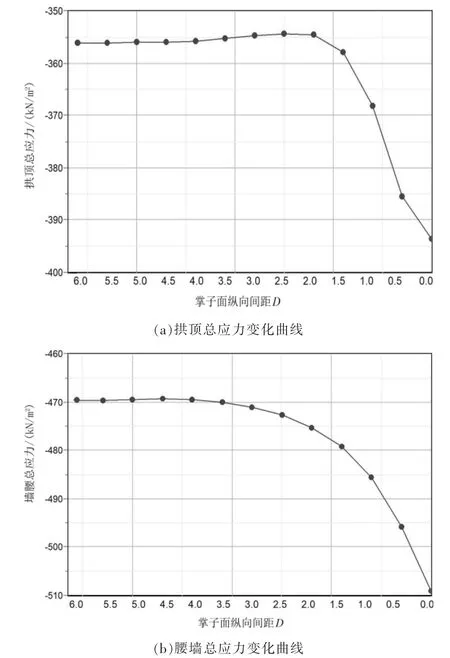
圖6 先行洞拱頂腰墻應力變化曲線

3.3 中隔墻變形與應力分析

取右洞掌子面處中隔墻中心點為研究對象，對不同縱向間距條件下中隔墻變形與應力進行分析。圖7（a）為中隔墻中心點水平位移隨掌子面縱向間距變化曲線，從圖中可以看出，中隔墻中心點水平位移隨縱向間距減小而增加，以2.5D 為拐點，2.5D之前位移增長速率緩慢，2.5D 以后水平位移呈線性增大，因此保持掌子面縱向間距在2.5D 以上，可以減小相鄰左洞引起的中隔墻水平位移量。圖7（b）為中隔墻中心點水平應力隨掌子面縱向間距變化曲線， 通過觀察可以發現， 掌子面縱向間距在6D～2.5D 間變化時， 中隔墻中心點水平應力值幾乎不變，以2.5D 為拐點，水平應力開始逐漸增大，同理，為減小相鄰左洞疊加在中隔墻上的應力值，掌子面縱向間距宜保證在2.5D 以上。

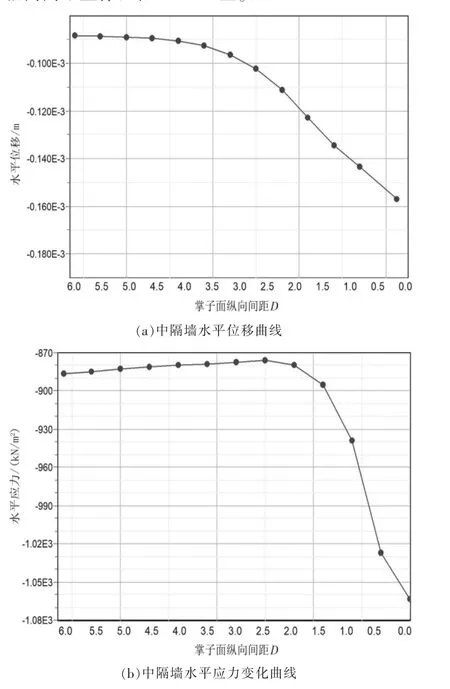
圖7 中隔墻水平變形與應力變化曲線

3.4 初期支護變形與應力分析

以右洞掌子面處初期支護結構為研究對象，對不同縱向間距條件下初支拱腰處總位移及軸力進行分析。圖8（a）為初期支護總位移隨掌子面縱向間距變化曲線，其線形同樣為拋物線形，初期支護總位移隨縱向間距減小而增加，以2.5D 為拐點，縱向間距在2.5D 之前總位移增長速率緩慢，2.5D 以后增長速率遞增并逐漸呈線性狀態，故為減小相鄰左洞對右洞初期支護變形的疊加影響，兩洞掌子面縱向間距宜保持在2.5D 以上。 圖8（b）為初期支護軸力隨掌子面縱向間距變化曲線， 該曲線以2.5D 為拐點， 縱向間距在2.5D 之前初期支護軸力幾乎保持不變，2.5D 之后軸力迅速增大，與上述結論相同，即掌子面縱向間距保持在2.5D 以上時， 可以減小相鄰左洞疊加在右洞初期支護上的應力。

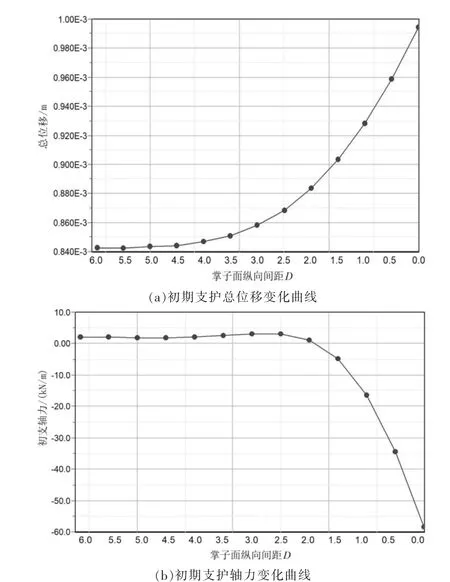
圖8 初期支護軸力與總位移變化曲線

4 結語

研究采用三維有限元數值模擬，在Ⅴ級圍巖基礎上，對不同掌子面縱向間距條件下連拱隧道地表沉降、洞周收斂變形與應力、中隔墻變形與應力及初期支護變形與應力分別進行計算分析，得到如下結論：

（1）連拱隧道左右洞施工開挖存在相互影響，在影響范圍內地表沉降及各項變形與應力均會互相疊加，且以2.5 倍單洞寬度為界，當左右洞掌子面縱向間距小于2.5 倍單洞寬度時， 兩洞相互影響明顯，變形與應力疊加顯著；當左右洞掌子面縱向間距大于2.5 倍單洞寬度時，兩洞相互影響減弱，變形與應力疊加不明顯。

（2）對于連拱隧道，為減小左右洞施工相互影響， 兩洞開挖掌子面縱向間距應保持在2.5 倍及以上單洞寬度。