固體火箭發動機變截面燃燒室縱向一維聲模態特性研究
史曉鳴, 侯凱宇, 劉陸廣, 高 陽, 夏 鵬, 李海東, 李莎莎, 陸豐瑋
(1. 上海機電工程研究所, 上海 201109; 2. 上海航天技術研究院, 上海 201109;3. 上海航天動力技術研究所, 上海 201109; 4. 上海航天精密機械研究所, 上海 201600)
固體火箭發動機是運載火箭、導彈等細長體飛行器廣泛采用的動力裝置。不穩定燃燒是國內外固體火箭發動機研制中屢次遇到的難題[1-3],其主要表現為發動機受擾動后,燃燒室內周期性壓強振蕩、平均壓強改變,發動機輸出推力振蕩、平均推力及工作時長改變,并伴有發動機及飛行器的劇烈振動,嚴重時導致發動機熄火或超壓爆炸,如圖1所示。對于聲不穩定機理的燃燒不穩定問題,是固體推進劑燃燒過程與燃燒室內聲振過程相互作用的結果。而固體火箭發動機往往是細長體構型,燃燒室內縱向聲模態頻率遠小于切向和徑向,往往控制著燃燒振蕩的發展[5],因此研究縱向聲模態對于固體火箭發動機的不穩定燃燒具有重要的意義!
經典的固體火箭發動機設計理論中常將燃燒室簡化為等截面圓柱形,以當地燃氣介質聲速a和燃燒室長度L,根據理論解fn=na/2L計算第n階縱向聲模態固有頻率。但對于翼柱型裝藥、雙脈沖等真實發動機,在燃燒過程中其內部燃燒室截面變化復雜,理論解往往得不到準確的結果。文獻[6-8]通過商業有限元軟件對變截面燃燒室聲模態的研究表明其縱向固有頻率與等截面理論解存在較大差異,且高階頻率不再是一階基頻的整數倍。商業有限元軟件通過對燃燒室三維幾何模型劃分網格進行數值計算可以精確分析復雜變截面燃燒室的聲場特性,但每次燃燒室裝藥幾何模型更改設計后都需要重新劃分網格再進行數值計算。因此,三維有限元模型不適用于固體火箭發動機初始方案設計階段的反復迭代優化及規律分析,更多的是用于最終設計狀態確定后的校核。
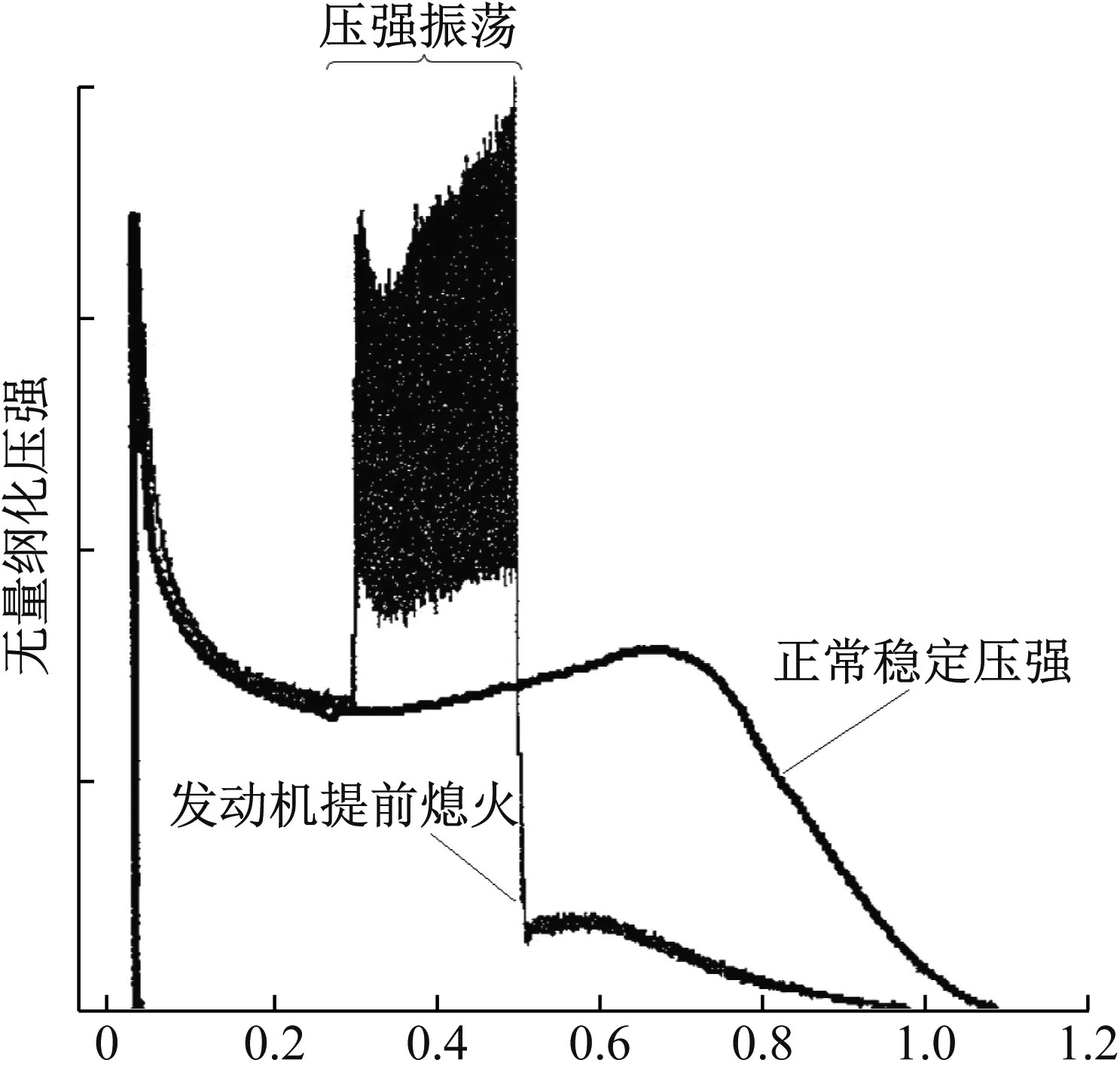
圖1 不穩定燃燒發動機燃燒室內壓強
考慮到固體火箭發動機細長體構型特征,燃燒室內燃氣流動可視作一維加質管道內流動問題。對一維管道內流體聲壓脈動研究是當前熱點。Carmicino等[9]通過求解一維波動方程的解析解,研究了固液混合火箭在點火工作過程中燃燒室軸向聲模態頻率的變化規律。Li等[10]推導了環形燃燒室聲場解析解,研究了非均勻截面和平均流場參數對聲場特性的影響。Yeddula等[11]提出了變截面管道中的聲波傳播的半解析解。蔡建程等[12]理論分析了不可壓縮流場壓力脈動(偽聲)與聲波方程的區別,并在CFD(computational fluid dynamics)數值研究直管與彎管入口處設置簡諧壓力脈動條件下管內非定常流動的特性。趙天泉等[13]設計了聲學試驗發動機,通過試驗研究前封頭結構及潛入空腔對聲穩定性的影響規律。
綜上所述,在固體火箭發動機設計過程中,商業有限元軟件可用于對三維燃燒室聲場特性的精確校核,但在方案階段的反復迭代優化設計上效率有所不足,且不便于直接分析截面變化對聲模態影響機理規律;而一維模型計算效率高,且數學模型是個參數化模型,便于分析及理解其相關參數對縱向聲模態的影響機理及規律。本文針對固體火箭發動機燃燒室縱向聲模態準確高效分析以及變截面對聲模態影響機理及規律研究的需求,建立考慮燃燒室截面面積變化的縱向一維聲振方程,有限差分數值求解縱向聲模態固有頻率及振型,分析了截面變化對燃燒室縱向聲模態特性的影響規律;通過變截面燃燒室模擬試驗件的聲模態試驗獲取脈動壓力響應,基于解析模態分解和希爾伯特變換辨識縱向聲模態參數,驗證了本文數值方法的準確性;并進一步應用于固體火箭發動機燃燒工作過程中縱向聲模態的數值仿真,分析其變化規律。
1 變截面燃燒室縱向一維聲振方程
固體火箭發動機燃燒過程中,隨著固體推進劑消耗,燃面不斷退移,燃燒室空間逐漸擴大,且伴有生成燃氣質量的注入,其所對應的聲振系統是時變的。但聲波在高溫高壓燃氣介質內的傳播速度遠快于燃面退移和燃氣生成質量注入的速度,因此可采用狀態凝固化的思想,將連續時變系統在時間上分割為若干個短時時不變系統,提取發動機工作過程中若干時刻的燃燒室幾何構型及該時刻的燃氣參數開展聲振分析。
固體火箭發動機工作過程中某一時刻變截面燃燒室內氣體滿足連續方程
(1)
動量方程
(2)
狀態方程
(3)
式中:ρ為氣體密度;A=A(x)為燃燒室截面面積;v為聲波脈動速度;p為脈動壓力;a為聲速。
(4)
式(4)對t求導得

(5)
式(2)兩端乘上截面面積A后對x求導得
(6)
(7)
(8)
(9)
2 有限差分法求解縱向一維聲振模態
對于縱向長度為L的燃燒室,沿縱向均布N個截面,將燃燒室均分為N-1段,每段長Δx=L/(N-1),第i(i=1~N)個截面上的面積及脈動壓力分別記為Ai,pi。
在第2~第N-1個截面上均滿足式(8),由此可得N-2個方程
(10)
(11)
(12)
式(12)代入式(10)、式(11)后聯立得矩陣形式的振動方程

(13)
式中:p={p1,p2,…,pN}T為脈動壓力列向量;M,K分別為聲質量、聲剛度矩陣。解廣義特征值(K-λM)·φ=0得聲振模態。
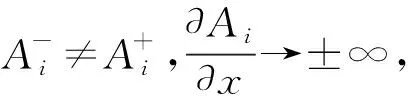
(14)
(15)
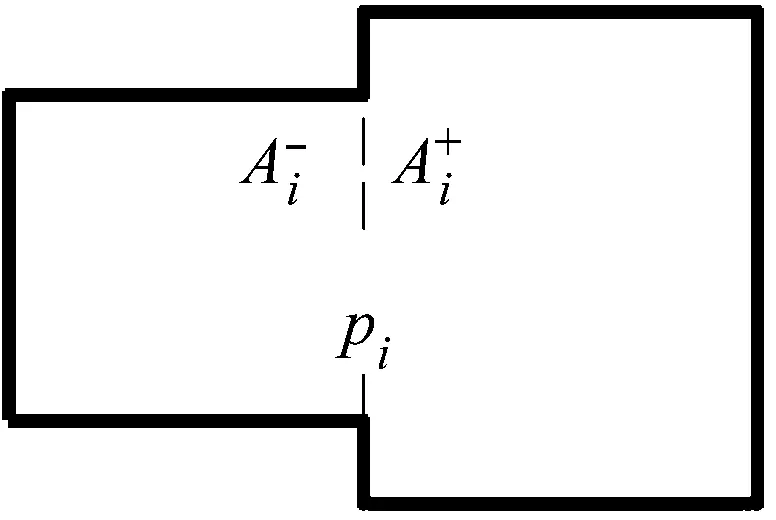
圖2 截面積階梯突變
以及脈動速度與脈動壓強的關系
(16)
可得
(17)
式(17)表明,脈動壓強對縱向坐標的偏導數在面積階梯突變截面的兩側不連續,截面兩側的偏導數與兩側的面積成反比。

(18)
式(18)代入式(17)得
4pi+1-pi+2)
(19)
式(19)替換式(13)中的第i行即可。
3 試驗驗證及聲模態辨識方法
真實固體火箭發動機點火試車試驗成本巨大,且搭載高溫高壓燃氣工況下聲模態試驗具有危險性。為驗證本文方法的準確性,設計了若干截面為圓形但截面面積沿縱向變化的燃燒室模擬試驗件,如圖3所示。包括截面半徑線性變化、截面積指數變化、截面積階梯突變、局部截面收縮等4組工況,用于模擬翼柱型裝藥、雙脈沖等真實固體火箭發動機中可能存在的各類截面變化情況。試驗件材料為2A12鋁合金,加工過程中,各試驗件一端已一體成型密封,另一端預留開口用于安裝喇叭,沿外表面一條母線鉆麥克風傳感器安裝孔,孔的位置及數量見圖3,截面半徑線性變化、截面積指數變化工況均為3個孔,截面積階梯突變、局部截面收縮工況均為5個孔,麥克風傳感器編號以最靠近開口端的位置為“1#”,依次遞增類推。
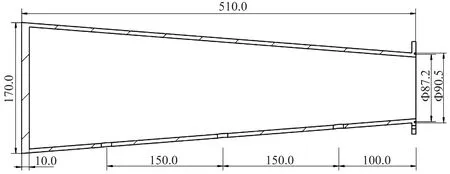
(a) 截面半徑線性變化

(c) 截面積階梯突變
進而開展了一個標準大氣壓下常溫大氣介質(聲速a=343 m/s)的縱向聲模態試驗。試驗系統及現場照片,如圖4所示。模擬試驗件放置于海綿墊上,在開口端安裝HiVi-Q3喇叭并嵌入O型圈密封,沿外表面母線預留孔安裝Microtech Gefell MM210麥克風傳感器并以硅膠密封,Lms.SCR05數據采集器輸出猝發隨機信號,通過DPM200A功率放大器驅動喇叭對試驗件內氣體介質施加聲激勵,數據采集器同時采集麥克風傳感器感受到的脈動壓力信號。

圖4 試驗系統及現場
試驗過程中喇叭實際對試驗件內氣體介質的聲激勵輸入不可測,只通過麥克風傳感器獲取了聲振脈動壓強響應。本文采用基于希爾伯特變換的解析模態分解和振動系統辨識方法從響應數據中識別聲模態參數。
對猝發隨機激勵下產生的自由衰減脈動壓強信號FFT(fast Fourier transform)后得聲振系統頻譜圖,如圖5所示。圖5中前3階諧振峰清晰易識別,表明本文對模擬試驗件采用猝發隨機激勵產生自由衰減脈動壓強信號的信噪比良好。以此確定各階聲振諧振頻率ωi,i=(1,2,…,n)。應用解析模態分解方法[14],選取若干二分頻率ωbi∈(ωi,ωi+1),i=(1,2,…,n-1),將脈動壓力信號x(t)表示為若干個單頻信號xi(t)的疊加
xi(t)=si(t)-si-1(t),
s0(t)=0,
si(t)=sin(ωbit)H[x(t)cos(ωbit)]-
cos(ωbit)H[x(t)sin(ωbit)],
i=1,2,…,n-1
(20)
式中:H·為希爾伯特變換;si(t)為頻率小于ωbi∈(ωi,ωi+1),i=(1,2,…,n-1)的信號,即低通信號;xi(t)即為本征模態信號。典型的自由衰減脈動壓強信號經解析模態分解后的本征模態信號,如圖6所示。各麥克風傳感器位置上的同一階本征模態信號周期相同,振幅及相位不同,對其進一步分析即可識別模態參數。
對每一階本征模態信號xi(t)應用基于希爾伯特變換的振動系統辨識方法[15-16]識別模態參數,系統第i階固有圓頻率ωi(t)表達式為
(21)
式中:A(t)為瞬態幅值或稱包絡線;ω(t)為信號的瞬態頻率。

圖5 聲振系統頻譜圖
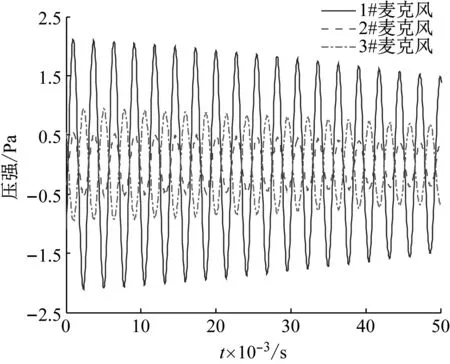
(a) 1階
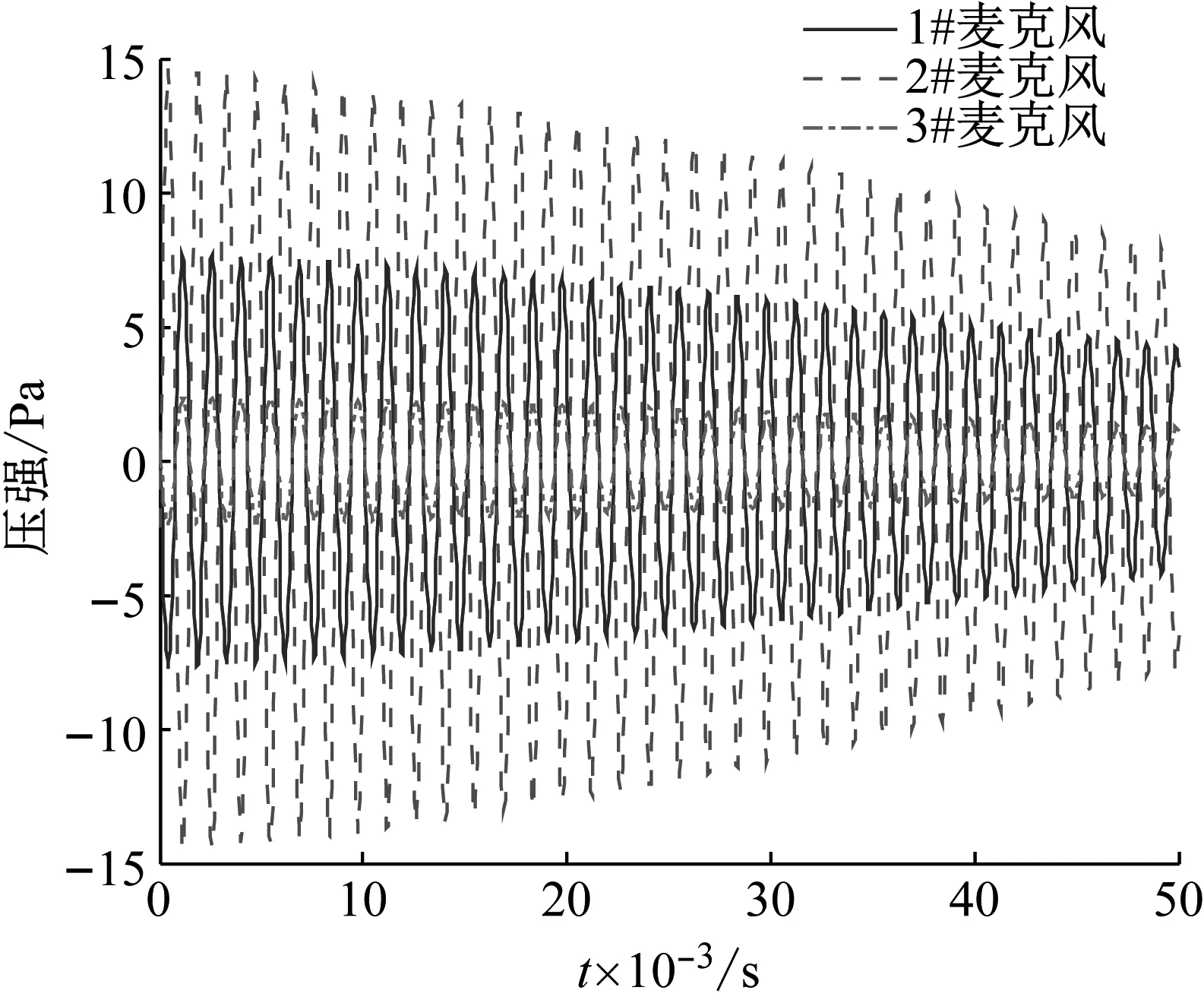
(b) 2階

(c) 3階
對于聲阻尼較小的系統,系統第i階聲模態在第a個傳感器測點上的振型可以表示為
Sia=Aai(t)cosψi/Abi(t)
(22)
式中:Aai(t),Abi(t)分別為a,b兩個測點上的第i階本征模態信號的包絡線;ψi為a,b兩個測點上的第i階本征模態信號的相位差。
4 結果與討論
4.1 變截面燃燒室模擬試驗件縱向聲模態
變截面燃燒室模擬試驗件縱向聲模態頻率采用本文方法計算、有限元軟件ABAQUS三維實體模型仿真以及試驗結果及其對比誤差,如表1、表2所示。從表1、表2中可見:本文方法與有限元仿真及試驗的結果比較均非常接近,截面半徑線性變化、截面積指數變化兩種工況下的計算與試驗結果誤差略微大于截面積階梯突變、局部截面收縮兩種工況下的計算與試驗結果誤差。這是由于麥克風傳感器安裝時,其咪頭需略突出于內表面以充分感受到壓強脈動,從而引起該安裝截面上的截面積局部小幅度突變,導致試驗與仿真結果之間存在誤差,如圖7所示;但在截面積階梯突變、局部截面收縮兩種工況下,試驗件本身存在較大幅度的局部截面積突變,故麥克風安裝引起的局部截面積變化對試驗結果的影響反而不明顯。
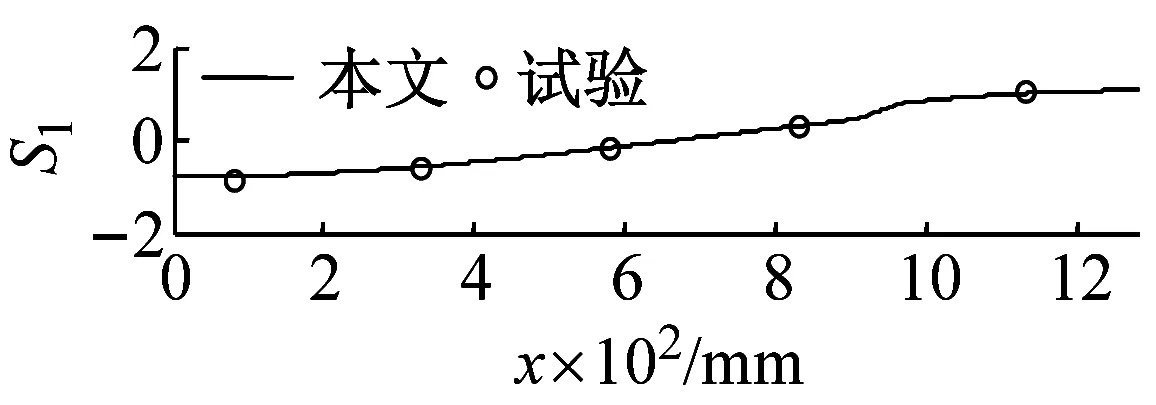
從表1中可見,變截面試驗件第n階(n>1)縱向聲模態頻率fn與 1階基頻f1之間的關系fnf1≠n,而是n-1 前3階縱向聲模態振型S1,S2,S3如圖8所示。圖8中左端對應封閉端,右端對應開口安裝喇叭端。本文約定以1#麥克風傳感器所在位置的振型為1進行歸一化,該位置在圖8各個圖中均為最右側的試驗測點。變截面工況下,縱向聲模態的奇數階振型關于縱向長度的中點不再保持反對稱,偶數階振型關于縱向長度的中點不再保持對稱:以與燃燒振蕩密切相關的一階聲模態為例,截面半徑線性漸變、截面積指數變化、截面積階梯突變等變截面工況的縱向聲模態振型的最大幅值均出現在截面積較小的一側端面,同時其振型節點位置與等截面振型節點相比,不再處于縱向長度的中點位置,而是從中點向截面積較大的一側移動;局部截面收縮變截面工況的縱向聲模態振型的最大幅值出現在中間收縮段的一側端面,同時其振型節點位置與等截面振型節點相比,不再處于中點位置,而是從中點向局部收縮段的一側移動。這是由于在變截面模擬試驗件內為同一氣體介質,氣體介質體積模量K是均勻分布的,但截面積A(x)沿著縱向變化,故各個截面上的氣體介質拉壓剛度K·A(x)沿著縱向分布是不同的,截面積較大區域其拉壓剛度較大,脈動聲壓的振型幅值會較小,由此必然造成節點兩側的振型不再保持對稱或者反對稱。 表1 縱向聲模態頻率 表2 縱向聲模態頻率結果誤差 圖7 麥克風傳感器咪頭安裝示意圖 進一步將本文方法應用于某內孔型裝藥真實固體火箭發動機燃燒工作過程中的縱向聲模態分析。取整個工作過程中歸一化時間tn=0,1/3,1/2,2/3,1共5個時刻的燃燒室幾何構型開展縱向聲模態分析。前3階縱向聲頻率變化規律,如圖9所示。在發動機工作的初始階段,其縱向聲模態頻率明顯小于等截面狀態下的頻率;隨著發動機燃燒工作直至熄火,縱向聲模態頻率逐漸單調上升趨向于等截面狀態下的頻率,直至最終接近等截面狀態下的頻率。 圖9 固體火箭發動機燃燒工作過程中縱向聲模態頻率 圖10 固體火箭發動機燃燒工作過程中燃燒室截面積變化 (1) 本文推導了考慮燃燒室截面面積變化的縱向一維聲振方程,有限差分數值求解縱向聲模態固有頻率及振型;設計了變截面燃燒室模擬試驗件,以聲模態試驗驗證了本文數值方法的準確性。 (2) 變截面燃燒室模擬件試驗表明:變截面工況下,縱向聲模態頻率第n階(n>1)縱向聲模態頻率fn與 1階基頻f1之間的關系fnf1≠n,而是n-1 (3) 對于內孔翼柱型裝藥結構的固體火箭發動機,在發動機初始工作階段,截面變化最為劇烈,工程中常用的將燃燒室簡化為等截面圓柱分析方法誤差較大,此時必須考慮截面變化的影響,從而得到更為準確的聲模態。


4.2 固體火箭發動機燃燒工作過程中縱向聲模態


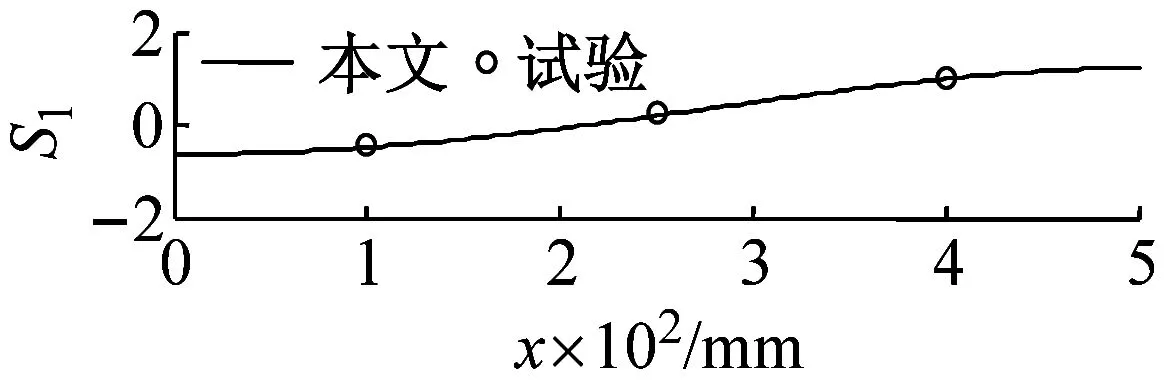
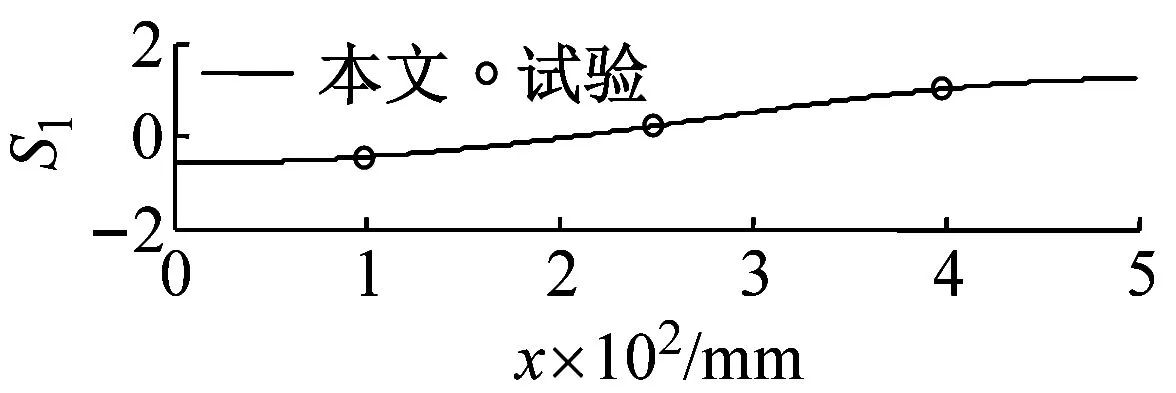



5 結 論

