基于Backroom Effect的生鮮品零售庫存決策優化

李 琳, 耿 彤, 張振民

(華東理工大學 商學院運營與供應鏈研究所,上海 200237)

0 引言

生鮮品，包括果蔬、肉蛋、奶制品以及水產品等，已經成為人們日常生活的必需品。統計顯示，我國消費者每周平均購買生鮮食品3次，其中果蔬類每周平均4.8次，水產類每周2.39次[1]。由于生鮮品具有易腐損的特性，作為生鮮供應鏈末端節點的生鮮零售商，一直致力于腐損控制以及與之相關的零售庫存管理。

圍繞生鮮品供應鏈管理，國內外學者進行了諸多研究，主要集中在訂貨決策、定價策略和供應鏈協調機制設計三個方面。王磊和但斌針對生鮮品易變質的特性，構建了與生鮮農產品新鮮度和價格相關的消費者時變效用函數，構建了零售商的生鮮農產品多品種訂貨模型[2]；Gregory等則將EOQ與需求受商品齡影響的生鮮易腐品訂貨策略結合，考慮了單一生鮮易腐品的庫存管理[3]。李琳和范體軍運用RFID技術來監控生鮮農產品，研究基于農產品實時價值損耗信息下零售商的定價與訂貨策略[4]；Li和Teng基于與生鮮品的銷售價格、參考價格、產品新鮮度和貨架展示量相關的消費者需求函數，建立了零售商的聯合定價和庫存模型[5]。曹裕等基于由單一零售商、供應商構成的二級生鮮供應鏈，比較研究兩個主體合作與否對二級供應鏈整體保鮮努力水平的影響[6];唐振宇等考慮了生鮮品在途損耗對產品數量的影響以及保鮮投入的影響，運用CVaR模型研究了零售商的風險規避程度對供應鏈決策的影響以及期權契約協調機制[7]。

而上述研究中，少有針對實際的生鮮零售賣場，區分前端貨架(Shelf)以及后端倉庫(Backroom)，探討包括倉庫-貨架補給以及訂貨補給的生鮮零售庫存管理。

事實上，在超市等零售賣場中，受限于賣場貨架的陳列空間，同一批次入庫待售的商品往往僅有小部分陳列于貨架供顧客挑選，而大多數都被存儲于倉庫中，而后通過倉庫-貨架的補給來保證前端的銷售[8～10]。Eroglu于2013年定義了倉庫在零售賣場的這種功能——Backroom Effect，認為后端倉庫的存在有效緩解了貨架陳列數量與進貨批量之間的矛盾，解決了overflow的存儲與銷售的問題[11]。在該定義下，零售商可以通過合理地運用Backroom Effect，調整賣場的貨架銷售策略[12,13]，進而提升其利潤[14]。

目前關于Backroom Effect的研究，多以耐用品為對象，而對賣場銷售占比較高的生鮮類產品關注不足。更重要的是，對于生鮮品這類具有易腐特性的商品而言，倉庫的Backroom Effect不僅僅體現在對overflow庫存的緩沖上，更多地體現在對新鮮度的保護上。

具體來說，首先，倉庫中存儲的待售商品保留了批量進貨的原包裝，使得其中的保鮮處理得以繼續發揮作用(如：箱內吸附型化學防腐劑可清除環境中的乙烯，或脫除過多的CO2而抑制果蔬的后熟)；其次，倉庫內的溫度、濕度等條件更為穩定，有助于生鮮品腐損率的控制，貨架盡管也多有冷藏設備，但是顧客直接接觸貨品，且諸多剝皮、捏掐等不良選購行為[15]都會加快生鮮品腐損，縮短其貨架壽命[2]。以香蕉為例，以箱為單位保存于倉庫的保質期約有21天，而陳列于冷藏貨架上的保質期則僅有短短的7天[16]。換而言之，生鮮品零售賣場的倉庫具有的Backroom Effect，既包括了學者們已經關注的數量層面的功能，更具有面向生鮮品所獨有的腐損控制和保鮮方面的作用。

在這種Backroom Effect下，倉庫對貨架補給后，貨架陳列的生鮮品數量和整體的新鮮度都會提升，刺激顧客的購買欲望。現實中賣場的銷售狀況與此極為相似，在同等售價下，每當有更為新鮮的商品被補充到貨架時，都會非常明顯地吸引顧客爭相選購[16,17]。因此，在生鮮零售中，考慮存在的Backroom Effect，分析其對貨架整體新鮮度和消費者需求的影響，對于零售商優化庫存和零售決策具有重要意義[17,18]。

本文基于生鮮品的特性和生鮮零售門店的實際，從數量和保鮮兩個角度重新定義了Backroom Effect。而后，考慮生鮮消費者需求的兩個敏感因素——貨架陳列貨品的數量及陳列生鮮品的整體新鮮度水平[17]，著力刻畫倉庫-貨架周期型補給下，Backroom Effect給貨架陳列生鮮品的新鮮度帶來的影響。并引入消費者“感知新鮮度”的概念，構造函數來描述貨架生鮮品實時的新鮮度及庫存變化，構建了以零售商利潤最大化為目標的最優庫存決策模型，為生鮮零售商的庫存決策優化和Backroom Effect下的投資決策提供參考。

1 問題描述及函數構建

考慮同時具有貨架和倉庫的生鮮零售商，倉庫因具有更佳的儲存條件而產生保鮮方面的Backroom Effect(后文簡稱為BRE)。t=0時刻到貨Q件生鮮品，由于貨架最大容量為N，故將貨架裝滿后，剩余Q-N件生鮮品被存儲在倉庫中。隨著消費者的購買，貨架庫存持續下降，現實中的零售商通常按照周期貨架補貨的方式——每隔時間T從倉庫中調配適量的商品補給貨架，使貨架陳列量達到飽和，直至倉庫庫存為0。當總庫存下降至臨界點，或到達生鮮品保質期時，剩余的商品將以殘值處理，零售商向供應商進行新一輪的訂貨。本文基于BRE，著力研究兩個決策問題：首先，倉庫對于貨架的補給，決策變量為倉庫對于貨架實行貨品補給的周期T；其次，整體庫存的訂貨補給決策，其決策變量為整體訂貨量Q和觸發整體訂貨的庫存臨界點r，對應于較為經典的(r,Q)庫存控制模型。

1.1 符號及假設

本文模型主要使用的符號及含義見表1。

表1 符號及其含義

由于生鮮品消費者的需求同時與兩個因素相關——貨架實時陳列數量，及貨架生鮮品的新鮮度水平[17,18]。我們采用現有文獻中普遍使用的乘積形式來描述需求函數[17,18]。

D(t)=α[Is(t)]β×Fc(t)

(1)

(1)式中的Fc(t)表示BRE和周期型貨架補給的情況下，消費者對于陳列生鮮品的整體平均新鮮度的感知(“感知新鮮度”)。顯然，這種感知新鮮度會直接影響消費者的購買意愿。接下來，本文將著力考慮貨架上不同新鮮度生鮮品共存的情形，刻畫整體平均的感知新鮮度函數，進而推衍感知庫存水平函數，探究BRE對于零售商貨架補給以及庫存訂貨決策的影響。

1.2 感知新鮮度函數和庫存水平表達

(1)t∈[0,T)未發生貨架補給階段

當t∈[0,T)時，由于沒有產生倉庫-貨架之間的補給，故貨架商品的新鮮度不存在差異，貨架和倉庫內生鮮品的新鮮度均以負指數e-λt衰減[17,18]，貨架庫存變化率為：

其中Is(0)=N，解微分方程可得貨架庫存水平：

(2)

對應的倉庫庫存水平為Ib(t)0=Q-N,則總庫存水平函數為:

Io(t)0=Is(t)0+Ib(t)0

(3)

當到達貨架補給時間T時，貨架剩余生鮮品的數量為：

(4)

(2)t∈[T,2T)發生第一次貨架補給階段

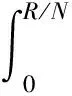
(5)

于是，當t∈[T,2T)，貨架陳列品的新鮮度按照貨架上的腐損速率λs持續衰減，

Fc(t)1=Fc(T)1×e-λs(t-T)t∈[T,2T)

(6)

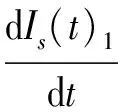
(7)

同時Ib(t)1=Q-2N+R1，則總庫存水平函數為:

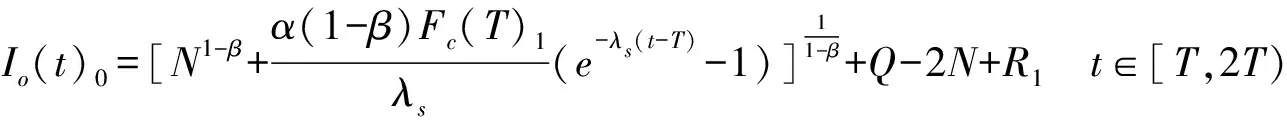
(8)

故可得第二次補貨時，即t=2T時，貨架剩余的商品數量：

(9)

第二次貨架補給后，貨架上的商品包括補貨前貨架剩余的R2件商品，和N-R2件新補給上來的商品，故2T時刻消費者的感知新鮮度表示為:

(10)

(3)t≥2T的階段

以此類推，當t∈[iT,(i+1)T)時，貨架商品的感知新鮮度和庫存水平函數如下:

Fc(t)i=Fc(iT)i×e-λs(t-iT)

(11)

(12)

第i次補貨時(t=iT)，貨架剩余庫存為:

(13)

第i次(i=2,3,4,…n)次補貨后，補貨點的感知新鮮度為:

(14)

1.3 BRE下的函數對比分析

盡管BRE在零售中普遍存在，但卻未被納入零售庫存決策的考慮范疇中。實際上，配合RFID技術和傳感器、物聯網的使用，BRE下貨架與倉庫間生鮮品實時腐損率/新鮮度都可以被測量估算和量化，完全可以為生鮮零售商所識別并運用于其零售決策中[18,20]。為了揭示BRE對零售商的影響，本節對比分析零售商忽略/考慮BRE情況下的關鍵函數。

在零售商忽略BRE的情形下，認為存放在倉庫和貨架的生鮮品具有相同的新鮮度，即λb=λs，周期型補給并不會帶來貨架陳列商品新鮮度的波動，即在任意時刻t，消費者對貨架產品的感知新鮮度均滿足：

Fc(t)i=e-λst)t∈[0,T)

(15)

易得t∈[iT,(i+1)T)時的庫存水平函數:

(16)

基于此，我們用上標1、2分別標識兩種情形(BRE下真實情形和零售商忽略BRE的情形)，著力對比其各自的消費者感知新鮮度和總庫存水平函數，得出結論如下：

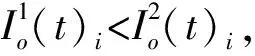
上述性質在圖1和圖2中得到了直觀的展示。觀察圖1，相比零售商忽略BRE的情形，BRE下真實的消費者感知新鮮度更高，且出現周期性波動，新鮮度的激增點即對應倉庫-貨架的補貨時刻。同時，由于BRE下新鮮度較高的生鮮品被補給到貨架上，使得貨架商品的整體新鮮度升高，進而刺激消費者購買，最終出現了圖2中BRE下總庫存下降速度更快的情況。由此而知，當零售商忽略BRE時，會導致實際消費者感知新鮮度及庫存量偏離預估情況，進而影響貨架補給周期、訂貨量等決策的設定。

圖1 兩種情形下的消費者感知新鮮度變化情況

圖2 兩種情形下的總庫存變化情況

2 庫存決策模型的構建與求解

2.1 決策模型構建

本節基于BRE，以訂貨量Q、倉庫-貨架補給的周期T和零售商向供應商訂貨的再訂貨點r為決策變量，以單位時間的利潤最大化為決策目標，構建貨架補給以及訂貨決策在內的生鮮零售庫存決策模型。

由(12)式，可得銷售周期內的倉庫儲存成本Hb和貨架儲存成本Hs分別為:

(17)

(18)

決策模型如下:

maxπ(Q,T,r)=(P×(Q-L)+V×L-Hb-

Hs-CQ-K-Cbsn)/Tn

(19)

特別地，再訂貨點Tn存在兩種情形：

Case1Tn=Te，即因商品到達保質期需向供應商訂貨，此時總庫存尚未降至r。此時，Te、Tns(倉庫庫存為0的時刻)和TR(總庫存降至r時的時間)之間的關系如圖3。圖3分別表示銷售時間到達保質期時，倉庫中有、無商品剩余的情況。

圖3 Case 1各時間點分布圖

Case2Tn=TR，即backroom中的產品能夠全部補給到貨架進行銷售，最后一次補貨后，當貨架庫存到達r時即觸發零售商訂貨。此時，Te、Tns和TR之間的關系如圖4。

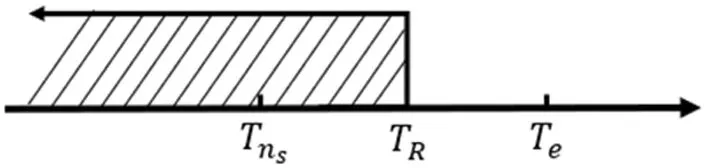
圖4 Case 2各時間點分布圖

2.2 決策模型求解

上述決策模型是包含非線性目標函數的非線性規劃模型，且模型決策變量為混合整數型(Q和r為整型)，與Bai和Kendall[17]構建的決策模型有相似之處，故選用其提出且已進行有效性驗證的改進GRG算法。具體地，將算法劃分為初始化、GRG求解(Excel Solver)和局部優化三個部分，思路如下：

表2 算法思路

3 數值計算與分析

本節分三個步驟進行數值試驗和分析：首先，對比BRE前后的相關決策與對應的利潤，驗證第1節的性質，揭示BRE對于生鮮零售商庫存決策的重要作用；接著，鑒于BRE直接反映于貨架和倉庫生鮮品腐損率之間的差異，分析該差異值的變化對生鮮零售商最優決策和利潤的影響；最后，考慮不同品類(自有腐損率不同)的生鮮品對于BRE的敏感度差異，通過對比其各自的最優決策及利潤，為零售商進行生鮮品的保鮮投資決策提供參考。

3.1 BRE前后的零售商決策對比分析

我們首先對六種不同的生鮮品(參數選自Bai and Kendall[18])，分別以λb=λs、0.5λs來表示零售商忽略BRE的情形和BRE下實際的情形，求解得到如表3的決策值及相應的利潤。表中，針對每一種生鮮品，第一行是零售商忽略BRE時的決策以及其預計的各項結果；第二行為按照零售商先前的決策(忽略BRE)，在BRE真實存在下產生的結果；第三行則是考慮BRE下的最優決策和相應結果。

從表3可以看出，六種生鮮品的庫存訂貨周期Tn均早于保質期Te(Te=7)，即零售商會合理地控制生鮮品的囤貨，避免因超過保質期而清空貨架、重新訂貨。同時，觀察每種生鮮品的第一行和第二行數據，可見零售商忽略BRE下的最優決策會導致實際的訂貨周期早于預計情況，該結果與1.3中的性質分析一致，此外，真實存在的BRE會帶來比預計更高的平均利潤(以生鮮品1為例：Tn:2.51VS.2.60,π:72.69VS.70.22)。進一步地，當零售商考慮BRE時，訂貨量和單位時間平均利潤均得到提升。由此可見，零售商若忽略了BRE，將會導致實際利潤和訂貨周期偏離預期，進而錯失提升利潤的機會。

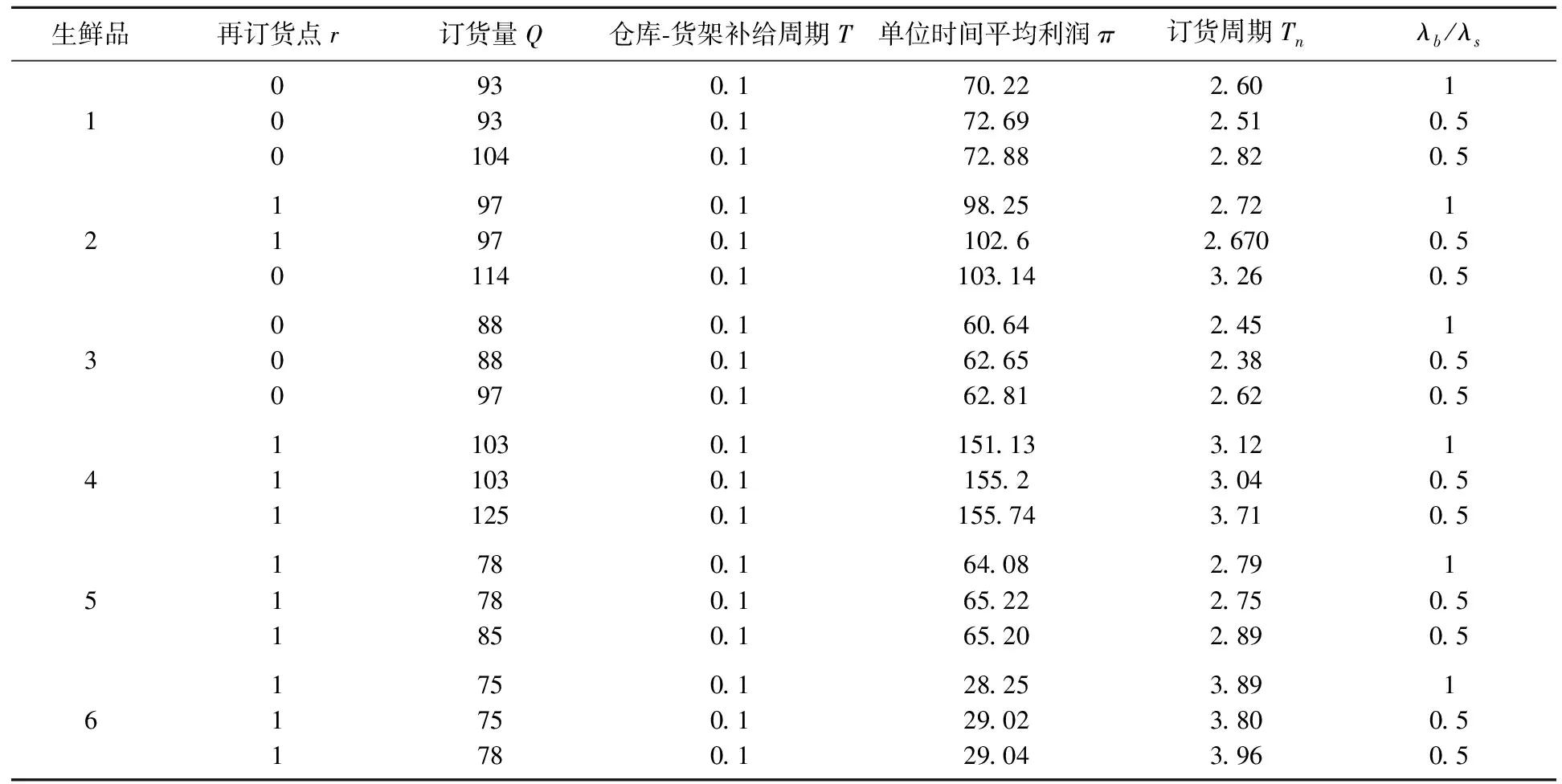
表3 模型最優結果

3.2 不同程度BRE下零售商庫存決策的變化

考慮倉庫的保鮮效果因溫度、濕度等條件的不同而存在差異，我們基于3.1的數值，分別取λb=λs,0.9λs,…,0.1λs，探究不同程度的BRE(不同的λb/λs)會對零售商的最優決策產生何種影響。得到多種腐損率比率下的最優決策，其中訂貨量和單位平均利潤增長率的變化分見圖5、圖6。

圖5 不同程度BRE對最優訂貨量Q的影響

圖6 不同程度BRE對單位時間平均利潤增長率的影響

由圖5可見，隨著倉庫對生鮮品保鮮效果的增強(即λb/λs逐漸降低)，六種生鮮品的最優訂貨量Q均得到提高，這是因為：λb/λs較小時，當倉庫對貨架補給后，貨架生鮮品的整體新鮮度提升幅度較高，消費者購買意愿大幅增強，促使零售商增加進貨量Q。同時，最優訂貨量的增加延長了銷售周期，進而增加了零售商的倉儲成本。以生鮮品4為例，當λb/λs的取值分別為1和0.1時，其對應的貨架、倉庫儲存成本分別為4.02VS.5.56，21.14VS.45.01，然而，由于較高程度的BRE提升了零售商的銷售收入786.34 VS.544.69，零售商仍能夠獲得較高的單位時間平均利潤151.13VS.160.27。即零售商可以通過平衡收入和倉儲成本來獲取利潤的提升。故從圖6中可以看出，BRE程度較高時單位時間平均利潤π的增長率也隨之增高。

因此，在BRE下，當零售商制定倉庫-貨架補給策略和整體訂貨策略時，應重點關注訂貨量的調整，且當BRE效果較強時，零售商可借機增大訂貨量，以提升利潤。

3.3 BRE下的零售商投資決策

本節將進一步探討對于不同品類的生鮮品(腐損率、價格、成本不同)，零售商應如何進行保鮮選擇才能更好地運用BRE，獲得最佳的利潤提升。

以3.1中生鮮品的各項參數為基礎，構建兩種類型的生鮮品A、B。其中，生鮮品A具有較高的售價、成本和腐損率(如：荔枝、草莓)，而生鮮品B的上述參數則較低(如：香蕉)，即生鮮品A具有更高的邊際利潤。我們根據Bai and Kendall[17]提供的參數表隨機生成了3組生鮮品：{生鮮品Ai，生鮮品Bi}(i=1,2,3)，各進行了10次實驗，得到不同程度BRE下零售商的最優決策，其中，訂貨量和單位時間平均利潤的增長率分別見圖7和圖8。

從整體上看，隨著倉庫對生鮮品保鮮效果的提升，三組生鮮品的最優訂貨量Q、零售商單位時間平均利潤π的增長率均逐漸升高。且A類生鮮品的增長速率均比同組B類生鮮品高。具體來說，隨著λb/λs從1降到0.1，三組生鮮品的訂貨量分別提升了{61%，9.8%}，{50.8%，5.8%}，{64.3%，10.4%}，單位時間平均利潤分別提升了{7.9%，3.3%}，{8.9%，3.5%}，{7.3%，2.8%}。究其原因，對高腐損率的生鮮品A而言，BRE的加深能有效維持其新鮮度處于較高水平，當倉庫中的貨品被補給到貨架上后，貨架商品的整體新鮮度顯著提升，進而增大了消費者的需求，由于其具有較高的邊際利潤，為零售商帶來了利潤的大幅增加；而對低腐損率的生鮮品B而言，由于其本身腐損率較低，故在貨架補給后，貨架商品的整體新鮮度提升幅度有限，對于需求量的影響相對較小，且生鮮品B的邊際利潤較低，因此零售商并未由其獲得利潤的大幅增加。

圖7 不同程度BRE對最優訂貨量增長率的影響

圖8 不同程度BRE對單位時間平均利潤增長率的影響

故在BRE下，零售商應重點關注邊際利潤和貨架腐損率較高的生鮮品，優先增強對這類生鮮品的保鮮，同時，借助BRE的提升，零售商可適當增大其訂貨量，從而擴大其為總體利潤增值的貢獻。

4 結論

本文從生鮮品的特性和生鮮零售賣場的實際出發，充實現有BRE的概念，重新提出了倉庫對于生鮮品的BRE——在數量上，倉庫通過不斷地補給貨架，緩解了貨架空間不足與批量訂貨之間的矛盾；在保鮮上，倉庫以穩定的冷藏環境，更有效地控制生鮮品的腐損率。基于此，考慮在周期型倉庫-貨架補給模式下造成的貨架上不同新鮮度商品共存的情況，本文從時間維度上構建了“感知新鮮度”函數，推演了時變的庫存水平函數，并與零售商忽略BRE下對應的函數進行了對比，發現當零售商忽略BRE時，會導致實際庫存量偏離預估情況以及訂貨周期提前。基于此，建立了考慮貨架-倉庫腐損率差異的最優貨架補給和訂貨決策模型，并通過多組數值算例分析了BRE下該腐損率差異對零售商庫存決策和生鮮品保鮮投資決策的影響。

通過模型構建、分析及數值算例的求解、對比，本文得出的主要結論包括：(1)周期型倉庫-貨架補貨模式下，BRE的存在可促使生鮮品零售商提升訂貨量，增加利潤；零售商若忽略BRE，則會錯失利潤提升的機會；(2)在考慮BRE的前提下，當BRE效果較強時，零售商應借機增大訂貨量，進一步提升利潤；(3)在BRE下，零售商應重點關注邊際利潤和貨架腐損率較高的生鮮品，優先強化對這類生鮮品的BRE效果，并隨之適當增大訂貨量，從而擴大其為總體利潤增值的貢獻。