基于組合導航系統的飛機自主著陸引導模式研究

鄒天嘉

（空軍駐南昌地區軍事代表室，江西 南昌，330095）

0 引言

飛機進場著陸是整個飛行過程中最重要且最危險的環節。在復雜氣象條件下，機場周邊可視條件較差，飛行員往往需要借助機上配置的儀表著陸或微波著陸引導設備接收機場地面引導臺站發射的引導信息進行輔助著陸。受限于電磁頻譜、地理環境等因素，國內很多機場沒有儀表著陸和微波著陸引導地面臺站。在這種情況下，機上的儀表著陸或微波著陸設備無法正常工作，進而導致飛行員無法從飛機顯示器上獲得引導信息。

對此，本文提出一種依托機載慣性/衛星組合導航系統（以下簡稱“組合導航系統”）提供的導航數據，經過坐標變換和換算，推算飛機相對理想著陸點的方位磁航向角度和下滑角度信息的方法。將獲得的角度數據與提前加載好的機場下滑道和跑道磁航向數據進行作差，自主計算出飛機實時的角度偏差值。按國際民航公約附件10的規定，將角度偏差值統一轉換為調制深度差值（DDM），形成可在飛機顯示器上顯示的偏差桿。

為實現自主著陸引導，可使用飛機配裝的組合導航系統提供的飛機的三維位置、速度、加速度、姿態角的導航數據，再結合飛機大氣系統提供的相對高度數據，進行偏差換算。

1 基于組合導航系統的飛機自主著陸引導模式

常規無線電著陸引導是在著陸機場當地的東北天坐標下進行的。飛機與著陸點的連線相對于地面平面的角度被稱為下滑角度，飛機與著陸點的連線在地面平面上的投影與磁北順時針的角度被稱為方位角度。對比飛機預定的下滑角度和方位角度進行作差，就可獲得飛機在兩個角度上實際值與預定值之間的偏差。

飛機上的組合導航系統和大氣機只能提供經度、緯度和氣壓高度數據，無法直接提供飛機在當地機場東北天地理坐標系下的三維坐標信息。因此，首先需要對經度、緯度和氣壓數據進行坐標變換，換算到機場東北天地理坐標系下的三維坐標數據后，才能進行下一步計算分析。

1.1 組合導航系統數據的坐標轉換

如圖1所示，組合導航系統能夠實時提供飛機的位置（經度λ、緯度L）、速度、姿態等信息，同時機上的大氣機提供標準氣壓高度數據H，因此可通過坐標轉換獲得飛機在協議地球坐標系下的三維坐標數據（x,y,z）。

圖1 經緯高與兩種坐標系之間的關系

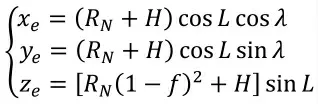
其中：λ為飛機的經度；L為飛機的緯度；H為飛機的標準氣壓高度；R為飛機所在地球位置卯酉圈的曲率半徑；f為地球的橢圓度（扁率）。

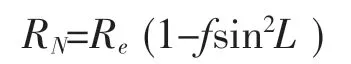
其中：R為協議地球的參考橢球赤道平面半徑（即長半徑）。

同理，在機場上跑道著陸點的經度λ、緯度L和標準氣壓高度H，可以求解出機場在協議地球坐標系下的三維坐標數據（x，y，z）。

在協議地球坐標系下飛機與著陸點之間的矢量坐標（Δx，Δy，Δz）可得：

將飛機與著陸點之間的坐標矢量由協議地球坐標系變換到機場的東北天地理坐標系內，以便于換算方位角和下滑角度。

將協議地球坐標系沿z軸旋轉（90°+λ），再繞坐標系x軸旋轉（90°-L），即可將飛機與著陸點之間的坐標矢量變換到機場的東北天地理坐標系(Δx，Δy，Δz）。

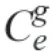
1.2 飛機方位角和下滑角偏差的計算

按圖2所示情景，飛機在進近著陸過程中的真北方位角α和下滑角β的表達式分別為：

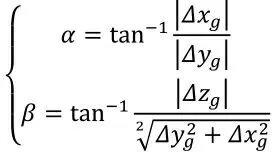
圖2 飛機方位角和下滑角在地理坐標系下的表達

1.3 飛機方位角偏差、下滑角偏差的DDM轉換

由于機上的無線電著陸引導系統輸出參數均采用歸一化處理，將角度偏差轉換為DDM偏差值（調制深度差）。因此，使用組合導航系統和大氣機換算出的飛機方位角偏差值和下滑角偏差值，也需要轉換為DDM差值，從而方便DDM差值在飛機平顯和下顯上的統一顯示。

根據國際民航公約附件10中的規定，機上方位角偏差角度與DDM差值之間的轉換公式為：

其中航向斜率與跑道長度D（D的最小單位為100m）有關，二者對應關系如表1所示。

表1 航向斜率與跑道長度的關系

與之類似，采用組合導航數據+大氣數據的方位角解算，可用公式實現慣導SCA模式下的DDM差值轉換：

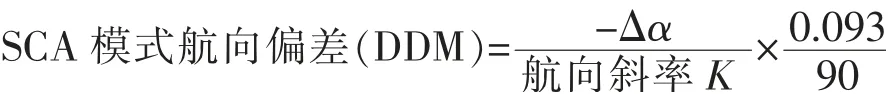
根據國際民航公約附件10中的規定，機上下滑角偏差角度與DDM差值之間的轉換公式為：

其中下滑斜率與飛機選擇的下滑角度有關，二者對應關系為：

與之類似，采用組合導航數據+大氣數據的下滑角解算，可用公式實現慣導SCA模式下的DDM差值轉換：

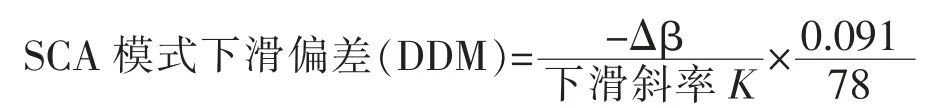
1.4 基于組合導航系統的飛機著陸引導精度分析

在使用組合導航系統進行自主著陸引導時，系統在三維坐標上的絕對誤差，不會跟隨飛機距離機場的遠近發生改變。因此，在采用此種模式進行著陸引導的過程中，其引導精度會隨著飛機距離機場著陸點的遠近發生改變。

設定在機場東北天地理坐標系下，著陸點的三維坐標位置為（x，y，z），飛機的實際三維坐標位置為（x，y，z），飛機慣導+衛星導航模式、大氣數據計算機的絕對氣壓高度一起計算輸出的三維坐標位置為（x，y，z）。

在組合導航系統可以實時接收衛星導航數據，從而不斷修正慣導輸出數據，使得系統位置精度始終保持在CEP≤50m。此種誤差為圓概率誤差統計，即定位計算出的位置（x，y）落在以飛機實際位置為圓心、半徑為50m的概率為50%，落在50m-100m范圍內的概率為43%，落在100m～150m范圍內的概率為7%，落在150m以外的概率為0.2%。

如圖3所示，組合導航系統提供數據的誤差，所造成的方位角偏差Δα可以表示為：

圖3 飛機實際方位角和解算方位角偏差示意圖

其中，D為飛機距機場著陸點的地面投影距離，r為誤差圓半徑。

由表2和圖4可知，使用組合導航模式進行輔助著陸引導，其只能在13km以外提供較為精準的Ⅱ類著陸標準方式的著陸引導所需的方位角信息。當飛機進一步接近機場著陸點時，其在方位角上的偏差將超過標準允許值，此時飛機下顯和平顯上的航向偏差桿只能起到參考和示意作用。

圖4 飛機方位角最大偏差與相對距離關系圖

表2 方位角最大偏差與相對距離的關系

根據相關標準要求，一般機載大氣系統的高度數據精度為：P（|r|≤3σ）≤±（7m或2%H取大者），因此氣壓高度需要分范圍區分均方差大小。

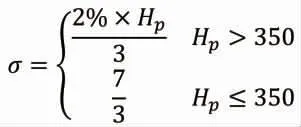
從圖5可知，由于大氣高度誤差影響，飛機正向最大下滑角偏差和反向最大下滑角偏差不同：

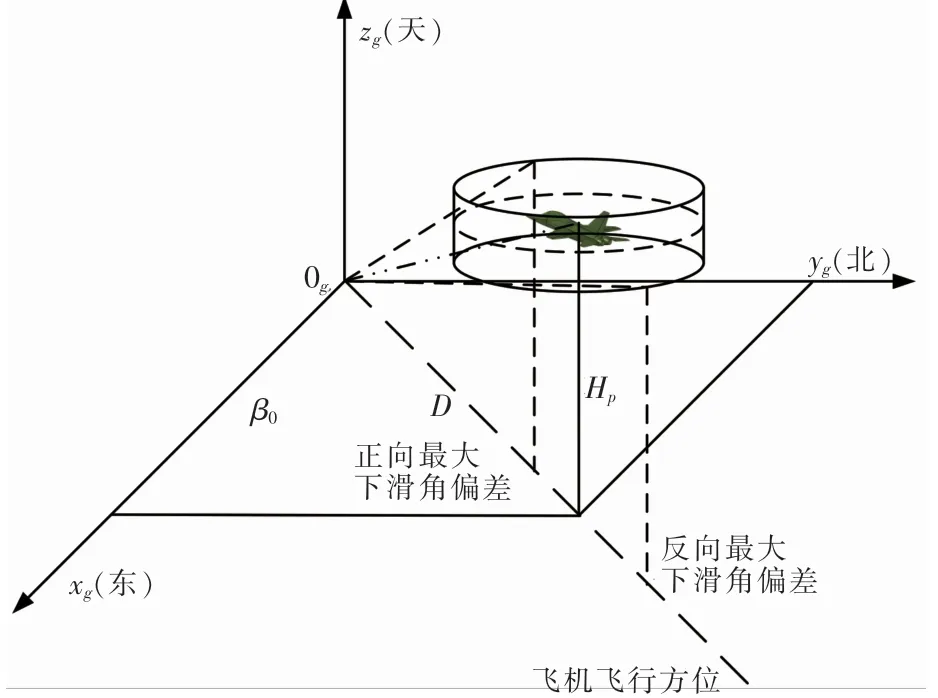
圖5 飛機下滑角最大偏差與相對距離關系圖

正向最大下滑角偏差Δβ為：

反向最大下滑角偏差Δβ為：

其中β為：

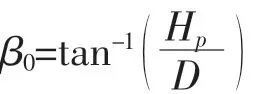
因此在距離相對較遠時，組合導航系統和大氣系統輸出數據，由于位置誤差相對整個著陸航線長度微乎其微，因此產生的偏差也較小，但距離機場越近，誤差越大，結果如圖6和表3所示。

表3 下滑角偏差范圍與相對距離的關系

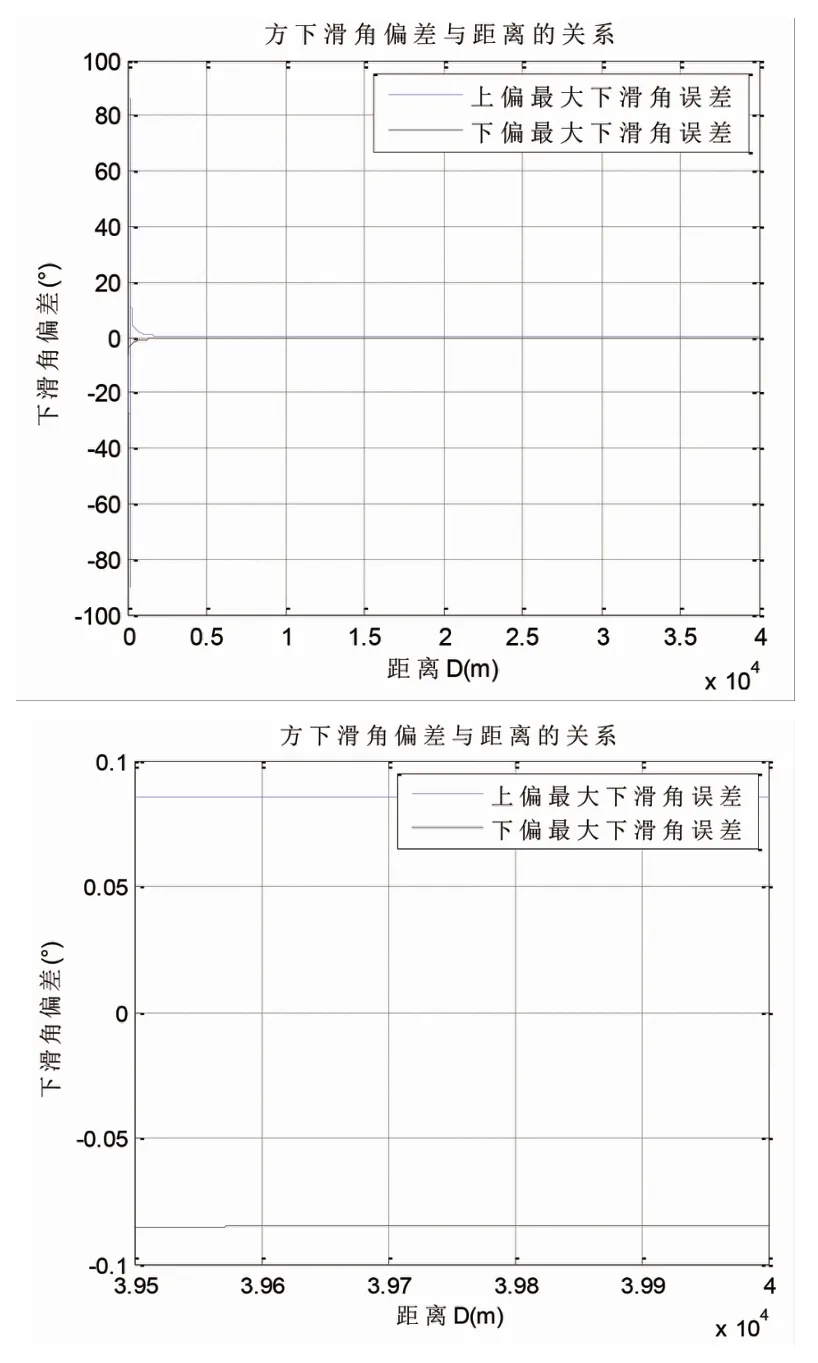
圖6 飛機下滑角最大偏差與相對距離關系圖

綜上可知，使用組合導航模式進行輔助著陸引導，其只能在680m以外提供較為精準的Ⅱ類著陸標準方式的著陸引導所需的下滑角信息。當飛機進一步接近機場著陸點時，其在下滑角上的偏差將超過標準允許值，此時飛機下顯和平顯上的航向偏差桿只能起到參考和示意作用。

2 組合導航系統的飛機自主著陸引導模式精度的仿真驗證

為驗證數據分析的正確性，在系統輸出數據中添加隨機誤差，對自主著陸引導系統進行仿真驗證。

2.1 飛機著陸下滑軌跡的生成

假設機場的跑道磁航向為30°，磁差為4°，則跑道真航向為34°，統一到當地地理東北天坐標系中，對應的飛機在水平面上的投影落在跑道真航向的延長線上，假定飛機距離著陸點的水平距離為D，則有：

對應的設定飛機下滑角度為3.6°，則有飛機離地高度z的表達式如下：

通過MATLAB仿真飛機下滑著陸的軌跡，假定飛機進場著陸的起始點距離著陸點水平距離為40km，飛行方向與跑道中心線重合，下滑角度為3.6°，則理論航向偏差和下滑偏差角度均為0°（即平顯和下顯的航向、下滑偏差桿為正十字），飛機在東北天坐標系下的飛行仿真軌跡如圖7所示。

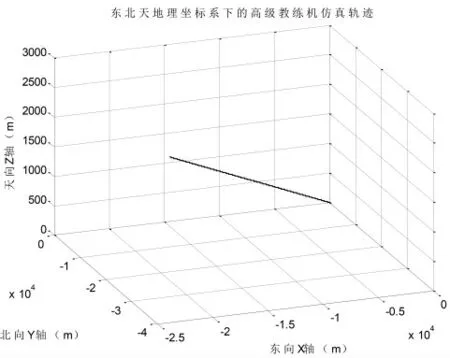
圖7 東北天地理坐標系下的飛機下滑著陸仿真軌跡

2.2 引入數據誤差的飛機運動解算軌跡

設定組合導航系統的水平均方差σ=52.1m，氣壓高度的均方差。

將組合導航系統誤差進一步分解為東向（x軸向）、北向（y軸向）的獨立誤差，根據誤差傳遞理論，對應的σ=52.1m，σ=52.1m。

在飛機著陸的每個仿真歷元中，分別在三個軸向上添加誤差，模擬機載組合導航系統和大氣系統實際輸出的數據，可得飛機組合導航系統和大氣系統數據，解析出的飛機運動軌跡如圖8所示。

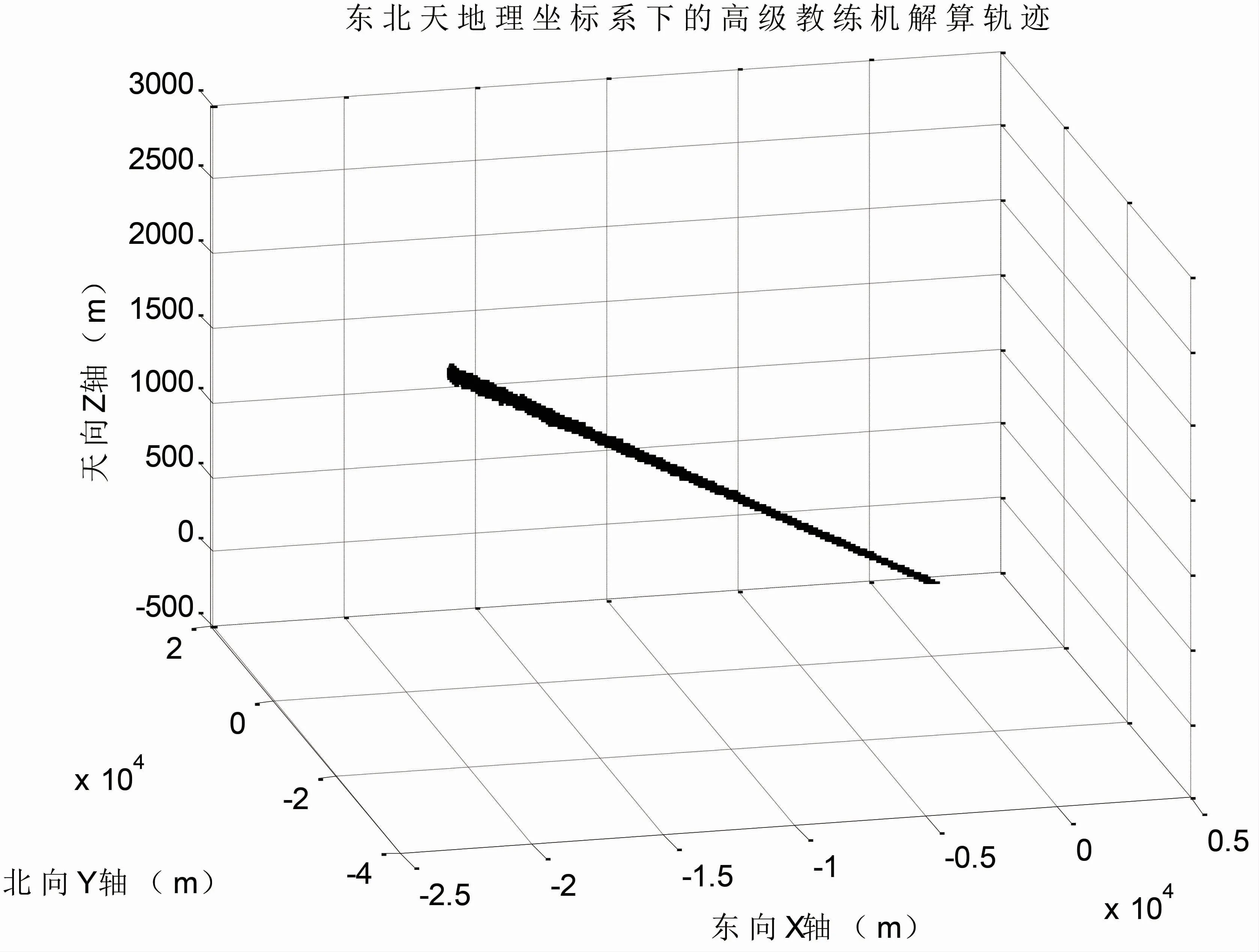
圖8 東北天地理坐標系下的飛機下滑著陸解算軌跡

2.3 飛機下滑著陸過程中角度偏差情況

分別在每個仿真歷元中，計算飛機解算位置相對飛機仿真位置之間的偏差信息，進而獲取飛機在下滑過程中每個歷元的方位角偏差、下滑角偏差信息，如圖9所示。

圖9 東北天地理坐標系下的飛機角度偏差與距離的關系

從表4可知，所有距離上方位角偏差和下滑角偏差均在理論分析的最大偏差范圍內，因此偏差精度范圍分析可信，可以作為引導策略的理論依據。

表4 角度偏差與相對距離的關系

3 基于組合導航系統的飛機自主著陸引導策略

通過對組合導航系統和大氣系統數據進行坐標變換，成功實現了輔助飛機進行自主著陸引導。但受限于組合導航系統的數據精度，其形成的自主著陸引導具有如下特點：

組合導航系統能夠穩定輸出一定精度的數據，可輔助引導飛機進行進近。但引導誤差會隨著飛機與機場之間距離的減小，成指數量級發散（尤其是方位偏差）。按照Ⅱ類進近著陸引導要求，該模式只能引導飛機抵達距離機場19.5km處。此后，隨著飛機距離機場越來越近，偏差桿將不再適用于精密引導：

1）在飛機到達距離機場9km時，方位角度偏差≯1°，下滑角度偏差≯0.12°；

2）在飛機到達距離機場3km時，方位角度偏差≯3°，下滑角度偏差≯0.3°；

3）在飛機達到距離機場1km時，方位角度偏差≯8.8°，下滑角度偏差≯1.1°。

結合無線電羅盤進近引導誤差0°方位允許偏差量±1°，因此在飛機飛抵距機場9km范圍時，建議主要采取目視方式，操縱飛機著陸。此后基于組合導航系統形成的自主著陸引導數據，精度置信度不高，建議僅作為參考使用。如在9km以內條件下，機場能見度無法滿足目視著陸的需要，則建議到氣象環境較好的備降場進行著陸。