鋼桁架結構平推過程穩定性能研究

張心純，陸澤磊，周 歷，任文輝，馬彥陽

(1.中鐵建陜西高速公路有限公司，陜西 西安 710064；2.長安大學 公路學院，陜西 西安 710064)

0 引 言

鋼桁架廣泛用于組合結構工程建造中，例如煤礦運輸專線、大空間結構等。鋼桁架-混凝土組合結構是將鋼桁架與混凝土橋面板通過剪力釘連接形成整體結構，能夠充分利用鋼桁架的空間穩定性能和混凝土的高品質抗壓性能，使其共同受力，變形協調，實現了優質組合，具有自重輕、跨越能力強、施工速度快、施工質量高等優點[1-2]。鋼桁架的應用不僅減少用鋼量，提升經濟效益，更積極響應國家結構工程建設綠色發展的時代號召，在工程結構產業轉型升級中具有較強的競爭力。

工程結構平推施工體系與施工工藝的不斷完善與創新，推動了平推施工建造技術的應用。對于大跨度鋼桁架結構體系，輕盈纖細的特點使得結構穩定問題成為平推施工過程中無法忽略的重要問題。結構失穩破壞具有突發性、破壞性大等特點，常造成橋梁結構垮塌等嚴重的安全事故，帶來重大的生命財產損失和惡劣的社會影響。

目前，有許多學者對結構的穩定性能及失穩破壞機理進行研究。YU等以新黃河大橋為案例對簡支鋼桁梁橋的受力性能進行了研究，對軌道-橋梁相互作用引起的地震反應進行了分析[3]。趙曼等建立了128 m跨徑的鐵路應急鋼桁梁非線性數值模型，系統分析不同荷載組合與非線性因素對結構穩定性能的影響，研究不同損傷狀態下的極限荷載[4-5]。施洲等基于鋼桁梁柔性拱橋有限元模型，考慮幾何和材料雙重非線性因素的影響，探究橋梁結構的穩定性能，系統分析鋼桁梁柔性拱橋的極限承載力[6-7]。夏正春等對鋼桁梁在恒載和活載作用下的穩定性能進行研究，指出加載方式對結構的穩定性能影響較大，隔跨布置活載對結構受力最不利[8]。趙雷等基于靜力試驗和數值模擬，探究初始幾何缺陷對桁架穩定性能的影響[9]。鄧海等基于車橋耦合振動理論，結合荷載試驗模擬分析鋼桁架在車輛荷載作用下桿件的軸力時程曲線[10]。張明等考慮多種關鍵因素影響確定桁架結構的最不利桿件，提出結構彈塑性屈曲承載力的計算方法[11]。ZHANG等通過風洞試驗和有限元模擬，研究了大跨徑板桁組合梁的顫振穩定性[12]。

在工程結構平推施工技術方面，趙人達等總結國內外橋梁頂推施工技術的發展概況，對頂推施工中導梁參數、施工控制等關鍵技術進行分析，探討未來發展趨勢[13]。CHACN等對鋼橋頂推施工過程進行試驗研究，并通過數值模擬對比分析結構的力學響應[14]。梁崇雙、王盛銘等分別提出不同鋼桁-混凝土組合梁施工及控制方案，探討頂推系統的設計方案[15-16]。DING等總結某連續鋼桁梁橋的懸索加勁弦桿頂推施工技術，并采用數值分析進行施工控制[17]。冀偉等研究在頂推施工過程在主梁內力的變化規律，提出導梁參數優化計算方法[18]。王金良等深入探究多跨鋼桁梁頂推施工中的偏移問題，通過數值仿真計算揭示軸線偏移對鋼桁梁桿件內力的影響規律[19]。時曉曄等計算分析鋼箱梁頂推施工過程中導梁屈曲變形特性，探究不同加固方案對導梁穩定性能的影響程度[20]。閆紓梅等對某鋼桁梁斜拉橋在施工最大單懸臂、雙懸臂及成橋等關鍵階段中的穩定性能進行研究，指出非線性因素對結構穩定性能影響明顯[21]。

文中選取某三跨鋼桁架-混凝土組合結構并建立精細化數值模型，針對鋼桁架結構平推施工過程的穩定問題進行深入研究，探究了導梁長度對結構受力與穩定性能的影響，提出了導跨比的合理范圍，對鋼桁架-混凝土組合結構的設計與施工提供了理論參考。

1 工程背景

選取煤礦運輸專線上某三跨鋼桁架-混凝土組合結構為研究對象，跨徑布置為3 m×80 m，單幅橋面寬12.5 m，雙幅橋面寬26 m，設計荷載等級公路-Ⅰ級。鋼桁架高度為8.3 m，其中桁高為7.8 m，混凝土橋面板板厚為0.4 m。鋼桁架一般構造圖如圖1所示。鋼桁架由箱型弦桿、箱型腹桿和工字型平聯組成，采用Q345qDNH高強度耐候鋼，在現場先焊接拼接后進行平推施工。鋼主桁的兩榀桁架之間通過工字型平聯進行橫向加強，在支點處截面采用斜向支撐加強橫向聯系，桁架間標準間距為6.7 m，各桿件關鍵截面構造參數見表1。橋面板采用預制C55高強度混凝土和1860級低松弛鋼絞線，行車道板寬12.5 m，承托處板厚0.4 m，懸臂處板厚0.24 m，鋼桁架之間處板厚0.3 m，通過與預留在鋼梁上翼緣的集束式焊釘聯結形成整體受力結構。

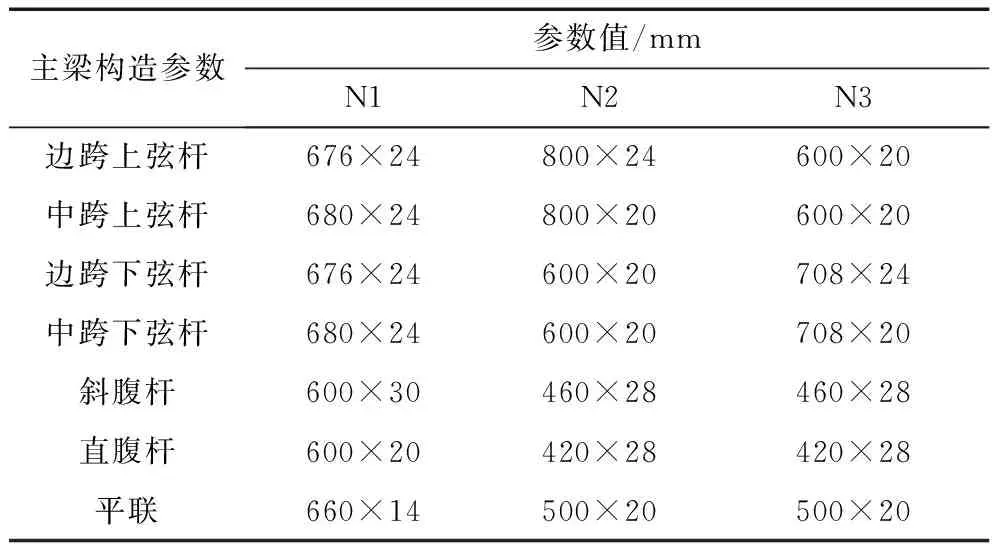
表1 桿件關鍵截面參數

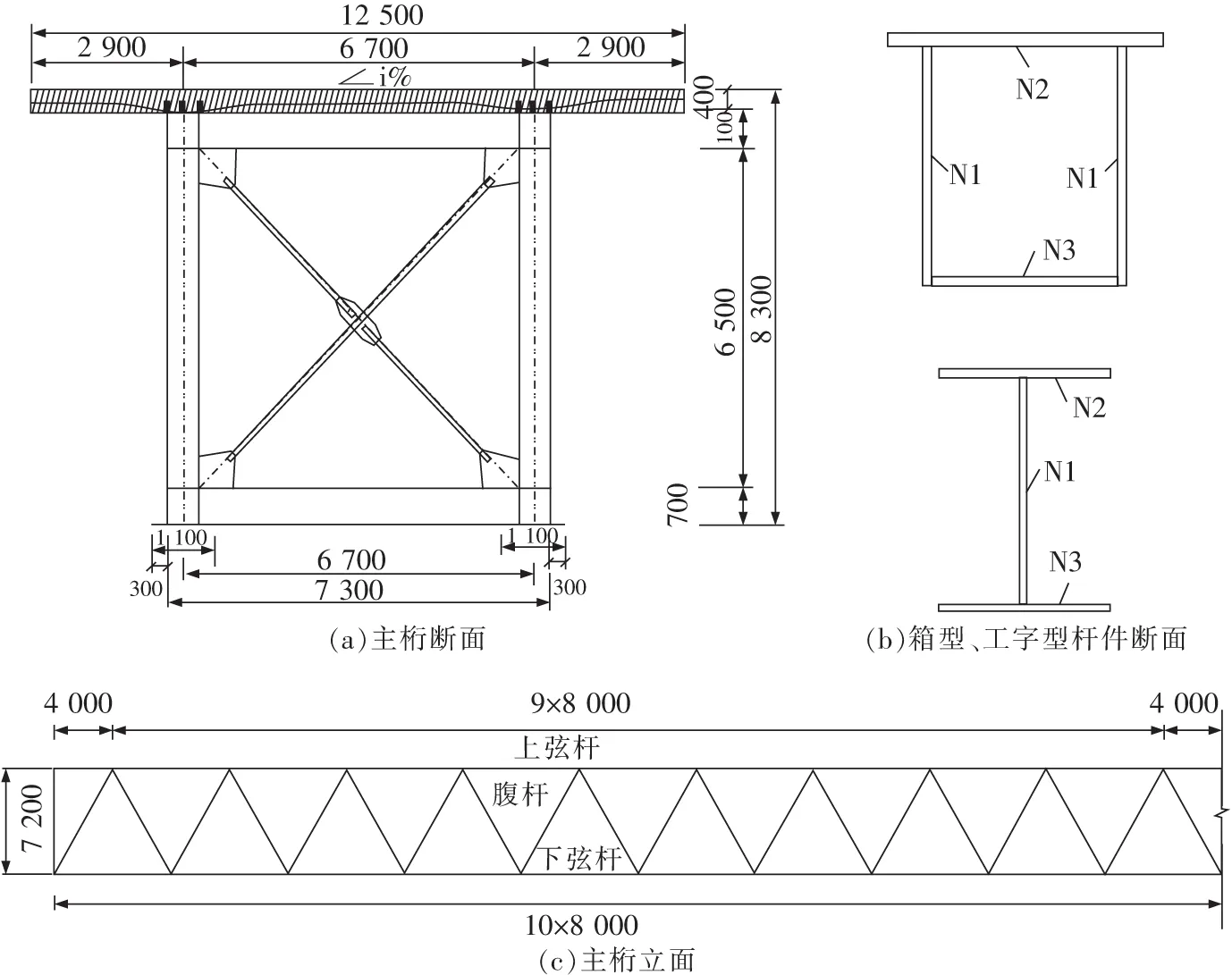
圖1 鋼桁架一般構造圖Fig.1 General layout of steel-truss

2 模型建立

為研究鋼桁架結構平推過程的穩定性能，選取與導梁連接的部分鋼桁架梁段作為研究對象，通過空間有限元軟件ANSYS建立鋼桁架模型，對端部支點處桁桿進行分析，鋼桁架-混凝土組合結構模型如圖2所示[22-27]。鋼桁架梁段模型通過桿件組裝的方式建立，鋼桁采用BEAM 188單元模擬，混凝土橋面板采用SOLID 65單元模擬，采用COMBIN 39非線性彈簧單元模擬桿件連接處的轉動剛度變化，在桿件之間建立傳力路徑使之共同受力。在模型建立時，不考慮橋面板與鋼桁架之間的剪力釘滑移效應，在橋面板與鋼桁架弦桿之間采用共節點連接，并忽略實際拼接過程中造成的桿件初始變位與焊接初始缺陷。

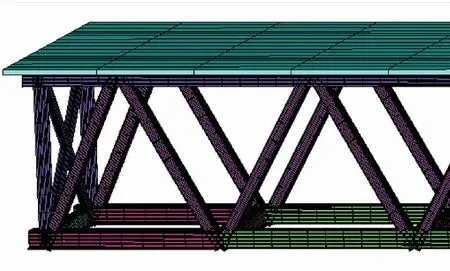
圖2 鋼桁架-混凝土組合結構模型Fig.2 Model of steel truss-concrete composite structure

3 平推過程梁段屈曲分析

在鋼桁架平推施工時，鋼桁各節段在聚四氟乙烯板和不銹鋼板滑道上現場拼接，采用步履式平推設備多點同步平推，每個梁段平推結束都均進行臨時約束。在平推過程中，鋼桁架的結構體系隨著節段前進不斷變化，桁架支點與導梁連接處桿件受力復雜多變。導梁作為平推施工體系中重要的施工輔助結構，不僅大幅減小了鋼桁架懸臂長度，有效降低了懸臂負彎矩峰值，對結構穩定性能的影響不容忽視。

選取導梁長度為0.6倍鋼桁結構主跨徑時，鋼桁架最大懸臂為32 m，結合鋼桁架實際平推過程，對鋼桁架結構采用特征值屈曲分析，得到其作為理想彈性結構的屈曲荷載，計算了結構在平推過程中的臨界荷載系數φ和臨界活載系數ω，并與鋼桁架成橋狀態時進行對比。

臨界荷載系數φ的含義為結構在荷載乘以此系數后的作用下可能出現失穩問題(屈曲)，假定結構全過程都處于線彈性工作狀態，采用特征值屈曲分析的方法求出結構發生第1類失穩時的臨界荷載系數。此時結構的屈曲荷載=臨界荷載系數φ×(恒載+活載)。臨界活載系數ω的含義為結構活載乘以此系數后的作用下可能出現失穩問題(屈曲)，采用臨界活載系數ω是因為結構恒載在全壽命期間基本不發生改變，需要進一步分析活載作用下的屈曲荷載，通過不斷迭代計算的方法使得臨界荷載系數φ等于1，此時屈曲荷載=1.0×(恒載+臨界活載系數ω×活載)。

臨界荷載系數φ和臨界活載系數ω計算公式見式(1)。

(1)

式中Fcr為結構屈曲荷載；FG為恒載；FQ為活載；φ為臨界荷載系數；ω為臨界活載系數。

圖3為平推過程中最大懸臂狀態與成橋狀態梁段臨界系數值與模態關系圖，由圖3可知，當鋼桁架處于平推施工階段的最大懸臂狀態時，更容易出現失穩破壞，平推過程中鋼桁架節段最大懸臂狀態時的前三階臨界荷載系數相比成橋狀態時，分別降低了13.14%，10.41%，10.85%，結構穩定性能下降明顯。成橋狀態下的各階臨界荷載系數波動較小，保持在4.8左右，而平推施工過程的節段最大懸臂狀態的臨界荷載系數隨著階數的增大呈現增加趨勢。組合結構的臨界活載系數隨各階模態的波動較大，平推施工過程中鋼桁架節段最大懸臂狀態時的前三階臨界活載系數相比成橋狀態時，分別降低了10.49%，8.72%，11.19%，對結構的穩定性能影響顯著。隨著模態階數的增大，降低幅度在減小，平推過程最大懸臂狀態第六階模態的臨界活載系數較成橋狀態減小了3.06%。

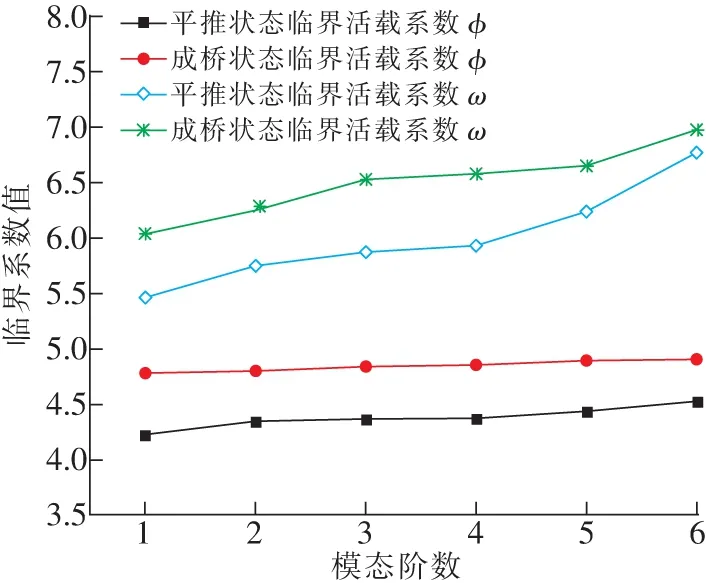
圖3 臨界系數值-模態階數關系Fig.3 Relationship between critical coefficient value and modal order

4 導梁長度影響分析

在鋼桁架平推施工過程中，導梁長度對鋼桁架懸臂梁段的桿件內力和結構的穩定性能均有較大影響，對平推施工順利進行起控制作用。為探究鋼桁架桿件和穩定性能在導梁長度影響下的變化規律，明確導梁長度的合理范圍，選取不同導梁長度與鋼桁架計算跨徑的比值α(導跨比)對桿件內力和梁段的穩定性能進行分析，桿件的選取如圖4所示。

圖4 平推施工示意Fig.4 Schematic diagram of incremental launching construction

4.1 導跨比對桿件內力的影響

為研究導跨比對桿件內力的影響，分別取導跨比為0.600，0.625，0.650，0.675，0.700，0.725，0.750，建立鋼桁架精細化模型對平推過程最大懸臂狀態進行數值分析，計算分析各導跨比下鋼桁梁平推到最大懸臂階段時端支點處梁段各弦桿、腹桿和平聯內力值。圖5為不同導跨比鋼桁梁各桿件內力值。

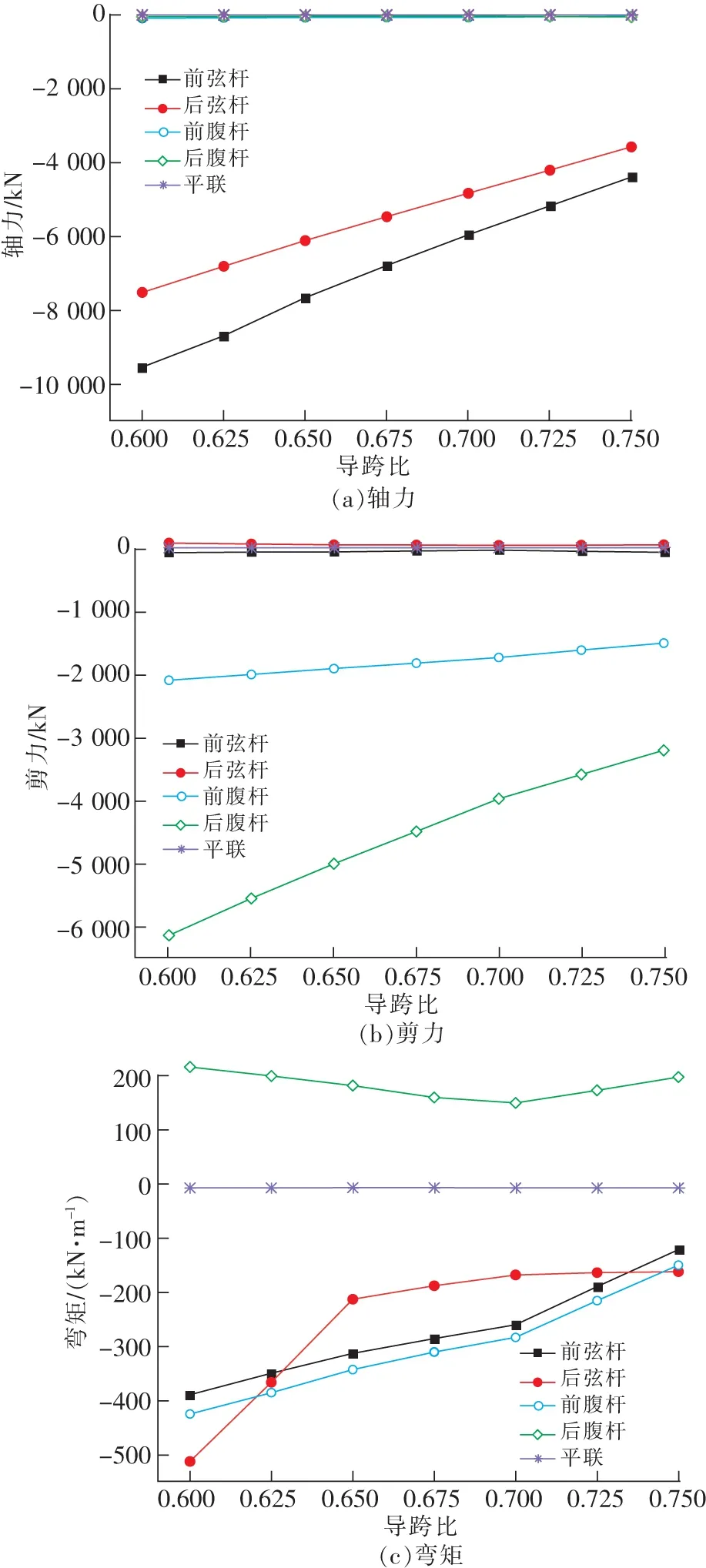
圖5 不同導跨比鋼桁梁各桿件內力Fig.5 Internal force of steel-truss members with different launching nose-span radio

由圖5可知，在鋼桁架平推施工過程中，最大懸臂狀態下的弦桿以受軸力為主，壓力最高可達到9 528.9 kN，腹桿以受剪力為主，剪力最高可達到6 133 kN，各桿件均受到一定程度的彎矩，平聯僅受極少彎矩影響。導跨比從0.600增大到0.750時，前弦桿所受軸向壓力從9 528.9 kN降低到4 387.8 kN，后弦桿受軸向壓力從7 509.4 kN降低到3 571 kN，降低幅度分別達到53.95%，52.44%；腹桿所受剪力從2 097.5 kN降低到1 508.7 kN，后腹桿所受剪力從6 133.1 kN降低到3 206.6 kN，降低幅度分別達到28.07%，47.72%。這是由于導跨比的增大，最大懸臂狀態下導梁的長度增長，而鋼桁架的長度減小，結構自重的變化導致懸臂狀態的彎矩減小，桿件內力得到優化。后弦桿所受軸力相比前弦桿減小幅度超過20%，前腹桿所受剪力相比后腹桿減小幅度超過50%，說明桿件間節點剛度對內力的分配有一定影響。

前弦桿和前腹桿的彎矩數值大小和變化趨勢相近，都隨著導跨比的增加而減小，且導跨比越大，減小幅度越多，導跨比從0.600增大到0.750時，前弦桿所受彎矩從389.3 kN·m降低到120.9 kN·m，前腹桿受彎矩從424.7 kN·m降低到149.7 kN·m，降低幅度分別達到68.94%，64.75%。后弦桿和后腹桿的彎矩變化較大，隨著導跨比的增加也呈現減小的趨勢，但是在導跨比較小時，彎矩變化幅度較大，在導跨比α=0.700時出現峰值，之后彎矩呈現隨著導跨比的增加而增大的趨勢。

4.2 導跨比對穩定性能的影響

鋼桁架作為橋梁結構的主體，在關注結構設計強度和剛度的同時，其穩定性能的重要性不容忽視，在荷載滿足材料設計強度的情況下，失穩破壞是結構主要破壞模式。鋼桁架穩定性能的影響因素，包括設計參數、結構尺寸、施工技術水平等。為研究平推過程中導跨比對鋼桁架結構穩定性能的影響，仍選取導跨比為0.600，0.625，0.650，0.675，0.700，0.725，0.750，對鋼桁架模型進行特征值屈曲分析，對比分析不同導跨比工況下鋼桁架的屈曲特征值。圖6為不同導跨比屈曲特征值-模態關系圖。

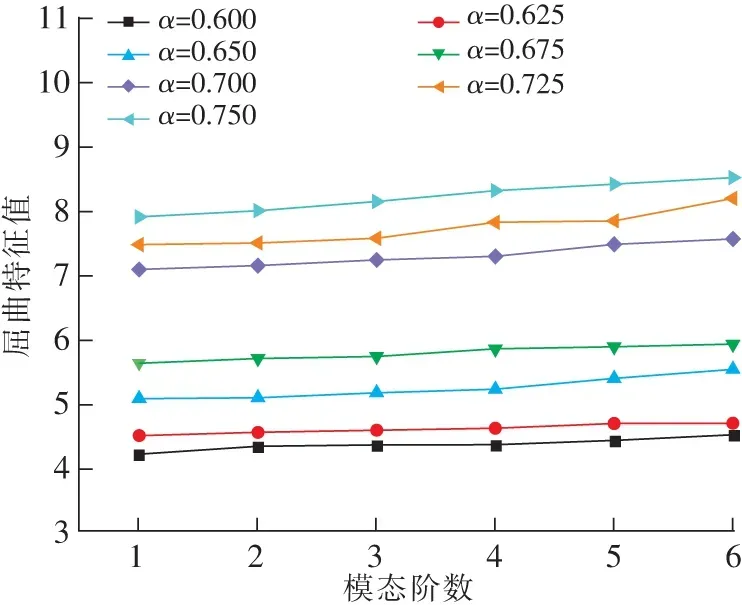
圖6 不同導跨比屈曲特征值-模態階數關系Fig.6 Relationship between buckling eigenvalue and modal order with different launching nose-span radio

由圖6可知，在同一導跨比下，結構的屈曲特征值均隨模態階數的增大而增大，且隨著導跨比的增大，結構屈曲特征值有不同程度的增大趨勢。從結構各階失穩模態發現，鋼桁架的破壞形態均是由桿件的局部屈曲造成的結構失穩破壞，導跨比的選取對結構屈曲破壞模式的影響較小，但對鋼桁架的穩定承載能力有較大的影響。

鋼桁架的屈曲特征值隨著導跨比的增大而增加，當導跨比從0.600增加到0.750時，結構的一階屈曲特征值分別提高了6.82%，20.44%，33.48%，68.08%，77.20%，87.43%，表明提高導跨比能夠有效提高結構平推時的穩定性能，且當導跨比從0.675增加到0.700時，結構臨界荷載系數增加幅度超過25%。結合計算結果與實際工程中導梁長度對其自身穩定性能的影響，建議在鋼桁架平推施工時導跨比的取值范圍在0.650～0.700之間。當導跨比因實際問題受限而小于0.600時，應采取設置臨時支架等措施提高結構穩定性能。

5 結 論

1)在平推施工階段的最大懸臂狀態時，鋼桁架結構的臨界荷載系數和臨界活載系數相比成橋狀態均較小，結構穩定性能下降明顯，結構更容易出現失穩破壞。隨著失穩模態階數的增加，平推施工狀態的臨界荷載系數和臨界活載系數逐漸增大，較成橋狀態的降低幅度不斷減小，結構穩定性能有所提升。

2)鋼桁架在平推施工的最大懸臂狀態時，端支點處弦桿以受軸向壓力為主，腹桿以受剪力為主，平聯基本不承擔軸力和剪力，僅受彎矩影響。

3)當導跨比從0.600增大到0.750時，結構自重的變化導致弦桿所受軸力和腹桿所受剪力均出現下降，前弦桿、后弦桿和前腹桿、后腹桿的降低幅度分別達到53.95%，52.44%，28.07%，47.72%。弦桿和腹桿的彎矩都隨著導跨比的增加而減小，其中后弦桿和后腹桿的彎矩導跨比α=0.700時出現峰值，之后彎矩呈現增大趨勢。

4)平推施工階段不同導跨比對結構屈曲破壞模式的影響較小，但對鋼桁架的穩定承載能力有較大的影響。當導跨比從0.600增加到0.750時，結構臨界荷載系數提高了87.43%，且當導跨比從0.675增加到0.700時，結構穩定承載能力提升幅度較大。

5)僅通過特征值屈曲分析方法研究鋼桁架結構平推過程的穩定性能，未考慮材料非線性和幾何非線性對結構穩定計算的影響，下一步將采用考慮結構初始缺陷的非線性屈曲分析方法研究鋼桁架結構的穩定性能。