地震作用下混凝土水池結構動力響應研究

張文斌，朱正瑜

(西北工業大學 基建處，陜西 西安 710072)

0 引 言

中國是地震多發性國家。在京津冀、長三角和珠三角城市群人口、財富高度集中地區，都曾多次發生6級以上強震。隨著時代的發展，鋼筋混凝土水池結構越來越廣泛的應用于實際工程中，特別是重大工程中，像泳池、實驗水池、渡槽等水池結構以及類似的儲液裝置越來越常見。大多數混凝土水池密集興建于近20年，尚未經歷過強震的考驗，大量混凝土水池或多或少都面臨一定程度的地震威脅[1]。福島核電站由于地震后引發海嘯致使二次供水系統失效，從而間接引發了核泄露，薛志成等人提出為了不重蹈日本福島核事故之覆轍，將儲存核電廠海水淡化區域大量淡水的工業水池系統作為核電廠應急水源，并將儲水池進行抗震設計的構想[2-5]。

鋼筋混凝土水池在地震力作用下，周圍土體與池內的液體會對池壁產生液固耦合(FSI)現象以及土與結構相互作用(SSI)[6-8]。FSI問題是研究液體與固體兩相介質之間的交互作用的問題。劉潔平等人研究地震力對混凝土水池的作用時，發現在地震作用下，高而柔的大型水池中的水產生晃動，由于池壁相對較柔，水的質量相對池身較大，甚至超過了水池本身重量，產生的動水壓力和沖擊壓力對水池動力特性和地震響應有很大影響[9-10]。在設計時若不考慮這種液固耦合相互作用，直接計算水池動力特性和結構反應，可能會得到過低的計算結果，對水池的抗震性能做出錯誤估計，在結構設計上存在隱患，致使在地震時可能會造成嚴重破壞和損失，甚至會引發次生災害[11-13]。

由于土壓力的存在，對結構的受力形式也有很大的影響。SSI對結構的動力特性以及地震響應有著很大的影響[14]。所以深入系統的研究不同條件下混凝土水池在地震下的受力特征，一方面可以保證混凝土水池的結構安全，另一方面對混凝土水池的設計也具有十分重要的參考意義。

1 模型建立

1.1 FSI作用的模擬

建立水池模型時采用以下假定：液體的密度不隨時間和空間變化；水池中的液體是無旋、不可壓縮和不可傳熱的；不考慮液體的凈流速，但考慮液體與池壁之間動力響應的相互作用；結構受水平方向單向的地震激勵。[15-16]

為了準確的實現液體和結構之間相互作用行為的模擬，必須建立正確的液體與結構池壁接觸界面處的邊界條件[17-18]。在建立FSI的邊界條件時，文中液體單元和結構單元分別建模，不共用節點，而是在相同坐標處分別建立液體單元節點和結構單元節點。假定水池底部為固定端，即節點所有自由度均被約束。液體與池壁接觸邊界處，對液體單元節點和結構單元節點耦合其法向自由度，使其在法線方向具有相同的運動，在切線方向可產生相對運動[19-20]。即液體與結構在池壁平面內可以產生相對位移，平面外相對位移為零。液體的暴露部分為自由液面。

為實現耦合界面處2種單元能準確耦合，應保證在耦合界面處液體單元與結構單元具有坐標相同的節點，即耦合界面處的液體單元節點和結構單元節點是一一對應的。這就需要在建模的過程中，耦合界面處的液體單元的面單元和結構單元的面單元完全重合且兩者具有相同的網格劃分尺寸。

在建立有限元模型的時候，由于水池池壁相對池壁的平面尺寸較薄，水池池壁可視為薄板，采用Shell 181單元實現模擬[21]。該單元是三維四節點單元，每個節點都具有3個平動自由度和3個轉動自由度，該單元適合分析薄板和中等厚度的板殼結構，不但具有分析板殼結構與薄膜力學行為的功能，也可考慮板殼結構的剪切變形，該單元能較好的模擬水池結構的地震響應。

液體采用Fluid 80單元模擬，在三維結構實體單元Solid 45的基礎上改進得到的一種三維容器液體單元，該液體單元是三維8節點單元，每個節點都只有3個方向的平動自由度。該單元是基于Housner模型簡化的三維液體單元。Housner模型將液體單元簡化成彈簧——質點體系，假定體系在激勵荷載下做線性響應，用線性的方法研究液體的響應行為。該單元適用于容器液體、無凈流速的液體的模型分析，以及有關靜水壓力的計算、液固耦合的計算和加速度效應等。該單元不允許退化為零體積，也不允許扭轉。

1.2 SSI作用的模擬

在地震作用下，池壁前后劇烈晃動產生較大位移，時而被土體推動，時而擠壓土體，土體對池壁的作用就類似于水平彈簧，側向土體對池壁就像彈性支承。隨著地震作用的變大，土體也表現出一種非線性行為[22-23]。

當池壁擠壓土體時，土體所提供的土壓力不能超過最大被動土壓力Pp當土壓力達到Pp之后，即便水池池壁位移繼續增大，土體所提供的土壓力也不會增大，而是繼續保持為Pp；當土體推動池壁時，土體所提供的土壓力不能超過最大主動土壓力Pa。土壓力達到Pa之后，即便水池池壁位移繼續增大，土體所提供的土壓力也不會增大，而是保持在Pa不變。

對于某些類型的土，特別是粘土，當結構往復晃動的時候，土體和結構可能會產生脫離或者不緊密接觸的現象。這時，土體提供的土壓力為零[24]。文中中假定土體是無粘性的，且不會產生裂縫。對于砂土和粘性土，我們采用Briaud和Kim推薦使用一種靜態的p-y曲線來進行擋土墻設計。土壓力和池壁位移關系如圖1所示。

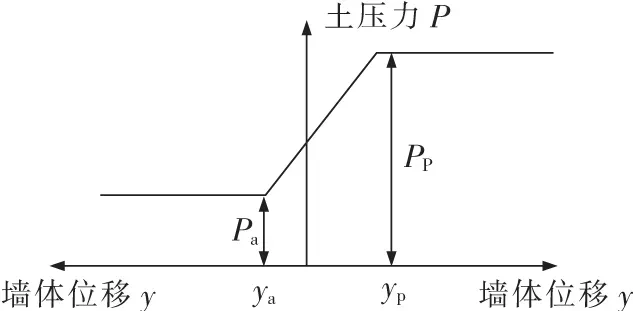
圖1 土壓力——池壁位移曲線Fig.1 Curve of the soil pressure-deflection of the wall

為便于在建模中實現該曲線，可將該曲線近似等效為圖2中2部分組合。

圖2 等效土壓力——池壁位移曲線Fig.2 Approximate representation of the soil pressure-deflection of the wall

從圖2中可以看出，土體作用在池壁上的土壓力可以分成2部分，第1部分隨水池池壁位移變化而變化，第2部分則不隨水池池壁位移變化而變化。

在建模的過程中，以節點集中力的形式來實現對面荷載的模擬。需將每個節點附近區域內的分布力等效為集中力，然后作用在節點上[25]。

土體作用在池壁上的土壓力依據圖2可以用水平非線性彈簧以及作用在池壁上的分布力分別來模擬。第1部分在建模中，采用Combine 39單元模擬水平非線性彈簧。因土壓力——位移曲線落在第1象限，因此可以設置關鍵字KEYOPT(2)=1使該單元只能受拉。在每個網格劃分的接點處都布置一個彈簧單元，每個彈簧單元的力——位移曲線都采用其所在深度的計算值。近似把該節點附近區域的土壓力視為該處的彈簧單元集中作用在池壁上。在池壁上直接施加梯度荷載來模擬第2部分的土壓力。

對于砂土，其最大主動土壓力Pa、最大被動土壓力Pp，以及對應的池壁變形ya和yp，將土體參數代入公式，即可得出對應土體對應的p-y曲線。

模擬第1部分的土壓力時，可在每個網格劃分的節點處都布置一個彈簧單元，近似把該節點附近區域該部分的土壓力視為集中力，通過該處的彈簧單元集中作用在水池池壁上。

在池壁上直接施加梯度荷載來模擬第2部分土壓力。通過計算，可以得出每個節點所承擔的該部分的土壓力。

選用2種不同性質的土體進行研究。其中堅硬土對應較硬的土體，軟弱土對應較柔的土體(表1)。

表1 土體參數

圖3為無水時的水池結構有限元模型。為方便下文敘述，現將4片池壁編號：y=0處池壁為池壁A；x=l處池壁為池壁B；y=w處池壁為池壁C；x=0處池壁為池壁D。如圖4所示。

圖3 無水時的水池結構有限元模型Fig.3 Finite element model of pool structure without water

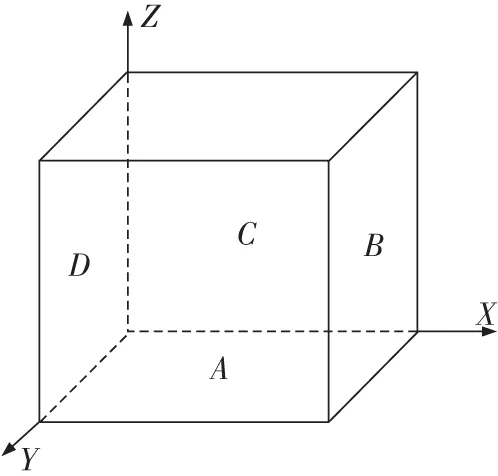
圖4 池壁編號示意圖Fig.4 Indication of the pool wall number

2 水池結構模態分析

在結構動力學中，系統的固有振動特性是由模態來描述的。在地震作用下結構的地震響應是表示結構體系自身特性的各階振型的組合。因此要分析結構的地震響應，必須先對結構進行模態分析[26]。

由于文中使用的液體單元是FLUID 80單元，選用縮減法進行模態分析。因此對于研究水池結構的動力特性，選取主自由度是非常重要的一個步驟[27]。縮減質量矩陣以及最后結果的精度取決于所選取的主自由度的數目以及位置。由于所采用的模型均只受到水平方向的地震波作用，因此選擇主自由度的位置在液面處的Z方向和池壁和液體相接處的法線方向。另外由于使用ANSYS在進行模態分析時會忽略材料的非線性，所以只考慮材料的初始切線模量[28]。

由于只有系統的前幾階振型對結構的動力響應的貢獻最大，所以不必求出結構所有的固有頻率及其所對應的振型，因此只需要求解出足夠多的前幾階模態即可，這將使得求解計算量大大減少。對模型進行模態分析，采用之前所述方法分別依據表2不同工況建立了4個模型：其中，水池尺寸均為30 m×30 m×9 m。得到不同工況下結構的固有頻率。

表2 不同工況下結構的固有頻率

從表2中可以看出，滿水工況下的水池結構固有頻率比無水工況下的固有頻率小。這是因為由于FSI作用的存在，液體單元的存在相當于對水池結構施加了一個附加質量，因此導致水池結構固有頻率的下降。

同時，堅硬土對應的結構固有頻率比軟弱土對應的結構固有頻率較大。因為堅硬土土質較硬，對結構的約束作用較為明顯，故其所對應的結構固有頻率較大。

3 水池結構地震響應

為了進一步研究考慮FSI作用和SSI作用的鋼筋混凝土水池結構在地震作用下的動力響應規律，對所建立的水池結構模型施加地震波，分析其動力響應。選取El-Centro加速度時程為輸入的地震波，地震波的輸入方向為模型的x向，并將加速度時程的峰值調至4.0 m/s2。

3.1 池壁厚度

為研究池壁厚度對水池結構動力響應的影響，建立5組不同池壁厚度的水池結構有限元模型。各模型的尺寸均為30 m×30 m×9 m(x×y×z向)。各模型的池壁厚度分別為：0.3，0.4，0.5，0.6，0.7 m。所選取的地震波為EL-Centro加速度時程，地震波的輸入方向為模型的x向，并將加速度時程的峰值調至4.0 m/s2。

底部環向等效應力峰值，指的是在水池結構的底面，從坐標x=0,y=0開始，逆時針旋轉，記錄每個節點在時程中的等效應力峰值以及其環向坐標。各個模型的底部環向等效應力峰值圖5所示。

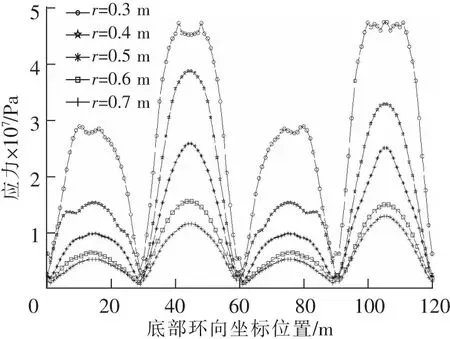
圖5 不同壁厚時底部環向等效應力峰值Fig.5 Peak equivalent stress of structure bottom with different thickness

x方向位移峰值，選取B面中部一系列節點，從水池底面到最高點處，記錄每個節點在時程中的沿x方向的位移峰值以及其坐標。各個模型的B面內x方向位移峰值如圖6所示。

圖6 不同壁厚時x方向位移峰值Fig.6 Peak delta of structure with different thickness in the direction of axis x

通過計算，可以發現。各個側面底部的等效應力峰值整體上表現出一種對稱性，一般在池壁兩端較小，在中部達到最大值。各組模型的等效應力峰值均在B、D面中部達到最大，4個角點處時程內應力峰值最小。當池壁厚度較小時，應力峰值在靠近中部的位置達到最大，然后在中部有小幅降低，但是整體上還是符合中部最大、兩端最小的規律，并滿足對稱性。從水池底面到最高點，節點的位移峰值是逐漸增大的，在最高點處達到最大。

隨著水池池壁厚度的增大，水池池壁的應力及位移逐漸減小。一開始減小幅度比較大，但是當水池池壁增加到一定程度時，減小幅度開始趨于緩慢甚至停滯。實際工程中，應綜合考慮應力及位移隨壁厚的變化規律，選擇合適的池壁厚度，使得應力和位移不至于過大，同時造價相對經濟。

3.2 平面尺寸

為研究水池結構的不同尺寸對水池結構動力響應的影響，建立有不同尺寸的水池結構有限元模型，并分析對比其在地震作用下的動力響應。地震波為EL-Centro輸入方向為x向，將加速度時程曲線峰值調至4.0 m/s2。

為分別對比不同的長、寬對水池結構的影響，分別改變水池在長、寬2個方向的尺寸，即平行地震波輸入方向(x向)及垂直地震波輸入方向(y向)。

3.2.1 長度l對水池結構的影響

所建立模型的長、寬、高，分別為18 m×30 m×9 m，24 m×30 m×9 m，30 m×30 m×9 m，36 m×30 m×9 m，42 m×30 m×9 m。

通過模擬計算，可以發現。隨著l逐漸增大，A面的底部應力峰值最大值與B面的底部應力峰值最大值的比值增大并逐漸穩定，其值依次為0.184，0.299，0.315，0.431，0.440。A，C面的底部應力峰值隨著l增大而增大。如圖7所示。

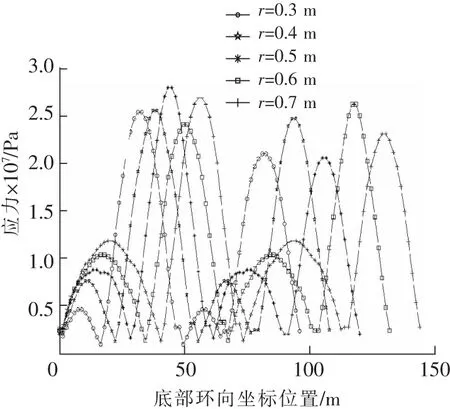
圖7 不同長度l時底部環向應力峰值Fig.7 Peak equivalent stress of structure bottom with different length

對于B面內x方向位移峰值而言，可以看出，隨著l的增大，其位移峰值基本不變。如圖8所示。

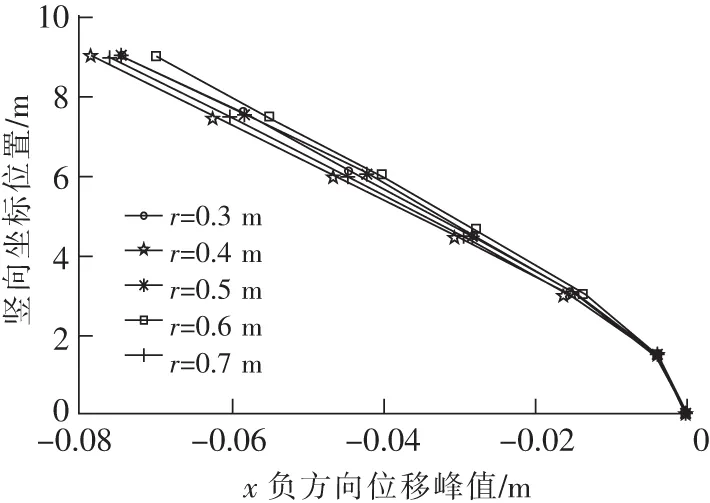
圖8 不同長度l時x方9位移峰值Fig.8 Peak delta of structure with different length in the direction of axis x

3.2.2 寬度(平行y向)對水池結構的影響

建立模型的長、寬、高，分別為30 m×18 m×18 m,30 m×24 m×9 m,30 m×30 m×9 m,30 m×36 m×18 m,30 m×42 m×9 m這5種尺寸。

通過模擬計算得出，隨著w逐漸增大，A，C面的底部應力峰值變化不大，B，D面的底部應力峰值逐漸增大。B面與A面的應力峰值的比值也隨著w的增大而逐漸增大且逐漸穩定，其值依次為1.212，2.138，3.171，3.21，3.365，如圖9所示。

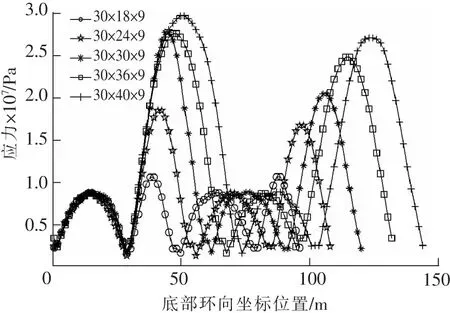
圖9 不同寬度w時底部環向應力峰值Fig.9 Peak equivalent stress of structure bottom with different width

從圖10各個模型的B面內x方向位移峰值可以看出，隨著w的增大，其數值均有明顯增大，呈現正相關現象。

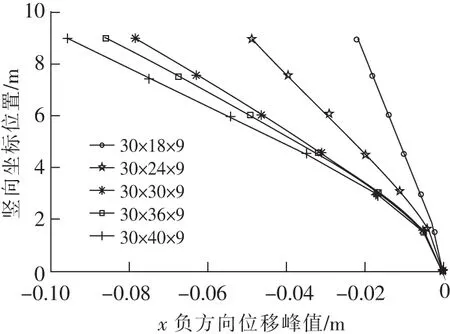
圖10 不同寬度w時x方向位移峰值Fig.10 Peak delta of structure with different width in the direction of axis x

結合l,w2個變量的變化，可以看出。當l,w其中一個變量不變，另外一個變化時，隨著l/w逐漸減小，A，C面的底部應力峰值與B，D面的底部應力峰值的比值減小，并逐漸趨于穩定。同時，該比值對w的變化更敏感。與地震波輸入方向(文中是x方向)相垂直的池壁平面(即B，D面)的尺寸增大時，位移峰值也隨之有明顯增大。而另一方向尺寸的變化對位移峰值沒有明顯影響。

3.3 不同土質

為研究不同土質對水池結構動力響應的影響，建立不同側向土的水池結構有限元模型，并分析對比其在不同地震波下的動力響應。所選擇的地震波為El地震波、VICT地震波、人工波。地震波輸入方向為x向，將加速度時程曲線峰值調至4.0 m/s2。

3.3.1 El地震波作用時結構動力響應

堅硬土所對應水池結構模型各個側面底部的等效應力峰值均表現出對稱性，并在中部達到最大值。在B，D面中部達到最大，4個角點處時程內等效應力峰值最小，如圖11所示。

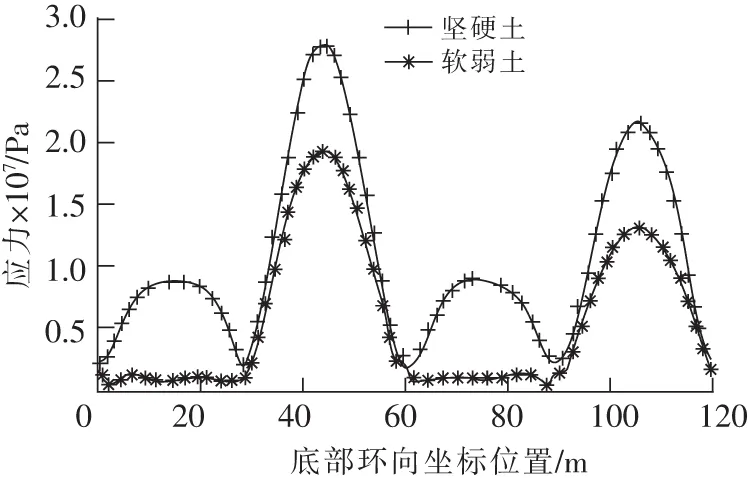
圖11 El地震波時底部環向應力峰值Fig.11 Peak equivalent stress of structure bottom

從水池底面到最高點，每個模型的節點位移峰值整體上都是逐漸增大的，在最高點處達到最大。同時堅硬土所對應模型的池壁時程位移峰值與軟弱土所對應模型的池壁時程位移峰值相比較大。也就是說土體主動推動水池池壁時，堅硬土造成的位移較大，軟弱土造成的位移較小，如圖12所示。

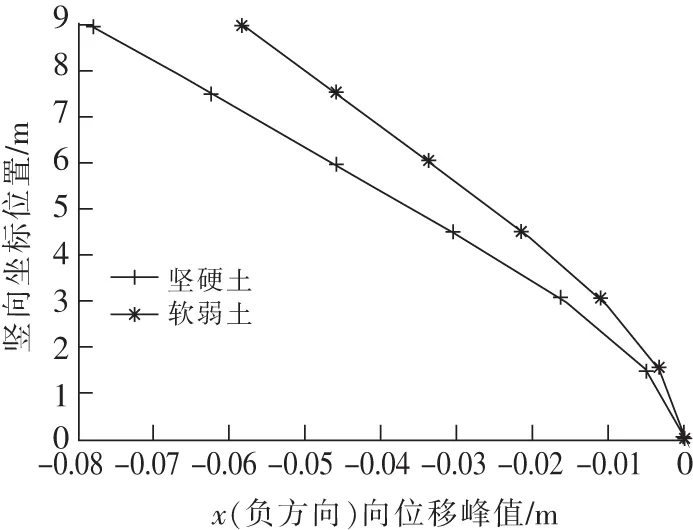
圖12 El地震波時x方向位移峰值Fig.12 Peak delta of structure in the direction of axis x

3.3.2 VICT地震波作用時結構動力響應

B，D面底部等效應力峰值分布表現出很明顯的對稱性，在中部達到最大，兩端應力較小。同時A，C面底部等效應力與B，D面相比小得多，如圖13所示。

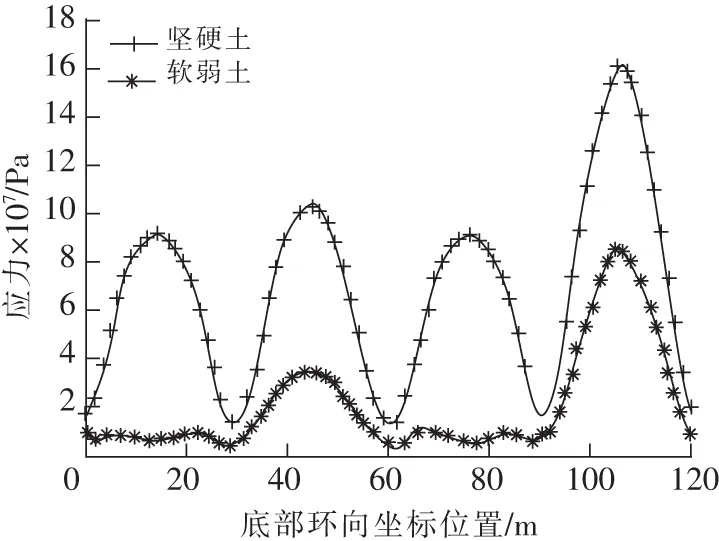
圖13 VICT地震波時底部環向應力峰值Fig.13 Peak equivalent stress of structure bottom

圖14是各個模型的B面內x方向位移峰值。此時水池池壁受到土體的主動推動，承受土體的主動壓力。

圖14 VICT地震波時x方向位移峰值Fig.14 Peak delta of structure in the direction of axis x

3.3.3 人工波作用時結構動力響應

圖15為地震作用下的各模型底部環向等效應力峰值，體現了堅硬土所對應模型的底部環向等效應力峰值與軟弱土所對應模型的等效應力峰值相比較大。特別是A，C面，堅硬土對應模型的等效應力峰值比軟弱土對應模型的等效應力峰值大得多。

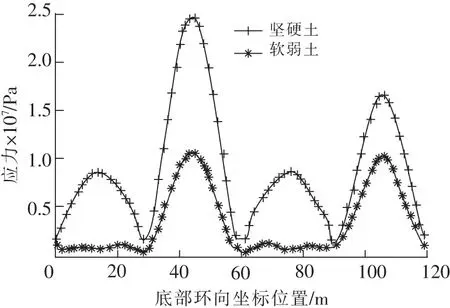
圖15 人工波時底部環向應力峰值Fig.15 Peak equivalent stress of structure bottom

圖16是各個模型的B面內x方向位移峰值，人工地震波所對應的數據圖表所表現的規律和El-Centro地震波所對應圖表所表現的規律一致。

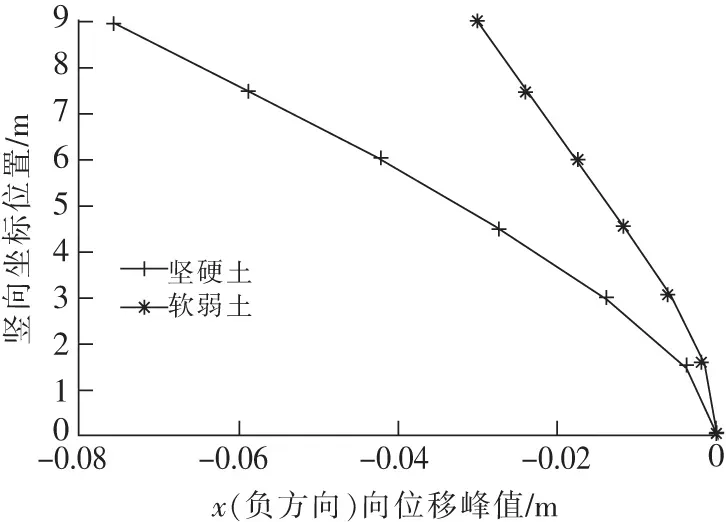
圖16 人工波時x方向位移峰值Fig.16 Peak delta of structure in the direction of axis x

軟弱土所對應結構，A，C面底部等效應力分布不均勻，曲線相對平緩，沒有呈現出對稱性，其最大值也并未出現在中部。而其B，D面底部等效應力分布則表現出很明顯的對稱性，最大值出現在中部，兩端應力較小。同時堅硬土所對應結構的底部環向等效應力峰值較大，特別是B，D面。

同時，當土體主動推動池壁時，堅硬土所對應模型的時程位移峰值與軟弱土所對應模型的位移峰值相比較大。

3.4 蓄水深度

為研究充水深度對水池結構動力響應的影響，建立5組不同蓄水深度的水池結構模型。各模型的尺寸均為l=30 m，y=30 m，z=9 m，池壁厚度均為0.6 m。各模型的充水深度分別為：0(即無水情況)、h/3,h/2,2h/3,h(即滿水情況)。

單條曲線即某一充水深度下的模型對應的底部環向應力峰值都服從相似的規律。各個側面底部的等效應力峰值表現出對稱性，并在中部達到最大值，4個角點處時程內等效應力峰值最小。各組模型的等效應力峰值最大值均出現在B，D面中部(圖17)。

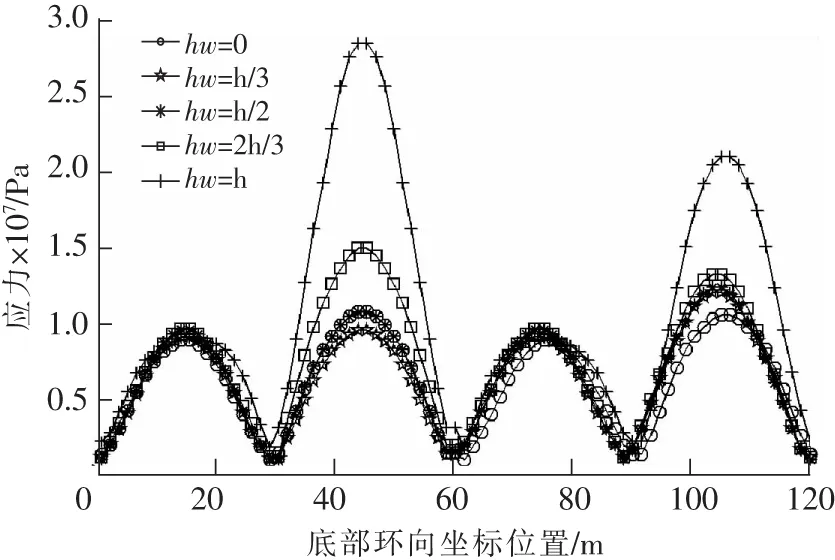
圖17 不同充水深度時底部環向應力峰值Fig.17 Peak equivalent stress of structure bottom with different depth

圖18是各個模型的B面內x方向位移峰值。可以看出，每條模型的位移峰值曲線對應的位移峰值都隨節點坐標的增大而增大，并且每條曲線依舊表現為彎曲型。明顯可以看到，隨著充水深度的增加，各節點位移峰值整體逐漸變大。當充水深度從0(即無水)增加到h/2時，位移峰值基本無變化。當充水深度超過為h/2時，位移峰值有明顯增大。

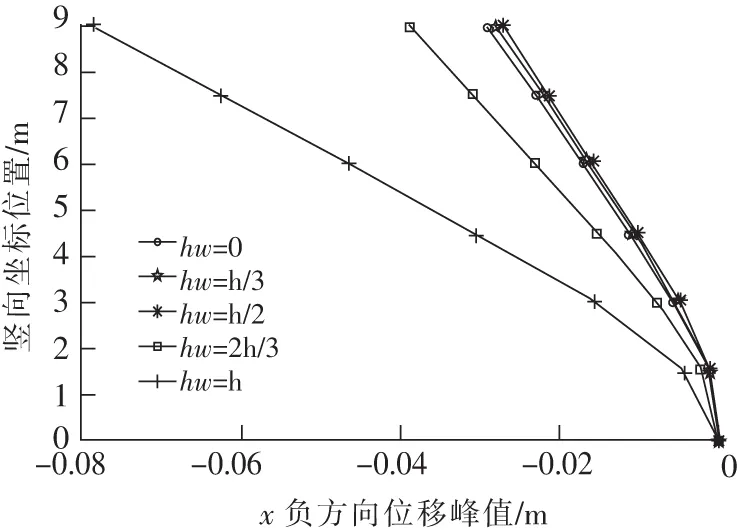
圖18 不同充水深度時x方向位移峰值Fig.18 Peak delta of structure with different depth in the direction of axis x

通過計算，可以看出，隨著充水深度的增大，水池池壁的等效應力峰值及位移峰值逐漸增大。一開始增大幅度比較小，但是當充水深度超過h/2時，等效應力峰值及位移峰值隨著充水深度的增加開始顯著增大，直至充水深度達到(即滿水情況)，等效應力峰值及位移峰值達到最大，且增大幅度較大。同時，A，C面的等效應力峰值隨充水深度增大只有略微增大，其增大幅度并不明顯，而B，D面等效應力峰值隨充水深度增加而有明顯的增幅。

4 結 論

1)水池在受到地震作用下，每個模型各個側面底部的等效應力峰值表現出一種對稱性，并在中部達到最大值。各組模型的等效應力峰值均在垂直地震波輸入方向的側面中部達到最大，4個角點處時等效應力峰值最小。

2)水池在不同土體包圍下，其受力形式區別較大，水池在堅硬土包圍下對應的結構固有頻率比軟弱土對應的結構固有頻率大。水池受到地震作用時，土體主動推動池壁時，堅硬土所對應模型的時程位移峰值與軟弱土所對應模型的位移峰值相比較大；堅硬土所對應的等效應力比軟弱土大，且在地震波輸入方向應力峰值較大。

3)地震作用下，隨著水池池壁厚度的增大，水池應力及池壁位移逐漸減小。一開始減小幅度比較大，但是當水池池壁增加到一定程度，減小幅度開始趨于緩慢甚至停滯。

4)水池滿水工況下的水池結構固有頻率比無水工況下的固有頻率小。地震作用下，當充水深度增大時，與地震波輸入方向相垂直的池壁平面(即B，D面)的等效應力峰值增幅較大，而A，C面則不明顯。

5)當水池的投影尺寸中，隨著l/w逐漸減小，A，C面的底部應力峰值與B，D面的底部應力峰值的比值減小，并逐漸趨于穩定。與地震波輸入方向相垂直的池壁平面的尺寸增大時，位移峰值也隨之有明顯增大。