電極移動速度對電容短路火花放電特性的影響
宋璐雯,劉樹林
(西安科技大學 電氣與控制工程學院,陜西 西安 710054)
0 引 言
應用在煤礦、化工等危險性環境下的電氣設備必須具有防爆性能。國際電工委員會規定采用IEC 60079-11:2006標準的安全火花試驗裝置驗證電路是否為本質安全型的電氣設備[1-2]。而隨著微控制器、傳感器的發展,低壓設備在危險環境下的防爆性受到了格外關注[3-4]。根據爆炸性混合氣體的臨界點燃電壓和電流曲線[5],通過試驗發現低壓電路發生火花放電并能夠引燃爆炸性氣體混合物[6-7],這與傳統的高壓火花放電及引燃機理不同。為探究基于IEC安全火花試驗裝置的低壓火花放電及引燃機理,需迫切研究電極移動速度、電氣參量等不同因素對火花放電特性的影響。
為此,國內外學者展開許多研究。鐘久明等通過分析不同氣氛條件下的火花放電特性[8]揭示容性電路的火花放電是以場致發射為主導的,且在此基礎上研究微間隙強場的形成與場增強因子有關,并推出金屬表面微凸起引起的場增強因子解析表達式[9]。UBER等研究發現IEC的兩旋轉電極在經過不同次數的火花放電后陰極表面形貌發生改變,形成更多的微凸起,且火花放電時間會更長[10]。由此可見,移動電極的放電過程是非常復雜的,移動電極在火花試驗過程中受到磨損與燒蝕,從而改變電極觸點形貌,使得各次的火花放電不同。電極間隙距離、材料、形狀、接觸方式和運動速度均會不同程度影響放電特性[11-14]。而火花的引燃能力與火花放電特性又密切相關。在引燃分析中,火花需要一定的功率和能量才能引燃爆炸性氣體混合物[15]。那么分析計算不同條件下的電參量與火花功率和火花能量的函數關系,是揭示低壓火花放電及引燃機理的關鍵方法之一。
由于容性電路火花放電時存在殘余能量和電路損耗,所以可通過積分算法得到火花放電的有效點火能量[16]。在針對IEC低壓火花放電點火研究時,通過建立指數函數放電模型[17],并結合積分算法得到火花能量的表達式。但是該模型的建模分析僅體現移動電極一次完全放電的特性。
因此,文中以IEC安全火花試驗裝置的移動電極為研究對象,基于Fowler-Nordheim理論,推導分析電極移動速度對微間隙場致發射電場強度及電流密度的影響變化,并通過電極不同移動速度下的火花試驗進行驗證;依據火花放電電壓特性,建立放電數學模型,推導分析電極移動速度對火花功率的影響規律,以及火花放電的能量極值。
1 移動速度對場致發射的影響
在強場作用下金屬勢壘高度變低,寬度變窄,依據隧道效應,電子克服金屬束縛從表面逸出,于是產生場致電子發射。
計算場致發射電流時,考慮電子的分布滿足費米-狄拉克統計,且以經典鏡像力來描述電子受到的金屬作用力。那么把在x方向上,從金屬內部到單位表面積動量在Px~Px+dPx范圍內的所有電子數dvPx進行積分,即得到場致發射的電流密度J的表達式為[18]

(1)
式中
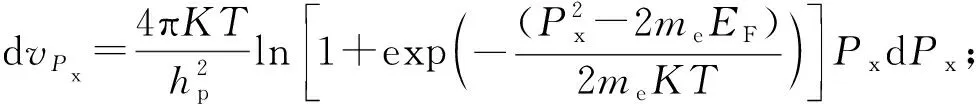
(2)

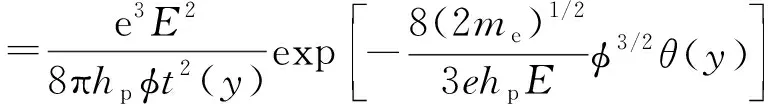
(3)
式中φ為功函數,鎘的功函數是4.07 eV;E為電場強度;y為Nordheim參數,y=3.79×10-5E1/2φ-1;θ(y)和t2(y)為關于y的橢圓積分函數,經簡化運算得到下式[21]。在計算時,認為式(5)的值近似為1.1。
(4)
(5)
考慮電極移動速度v對場致發射電流密度影響時,根據IEC火花放電電極特性,當極間電場滿足臨界擊穿場強時,發生場致電子發射,大量電子從陰極鎘盤表面逸出,自由電子在外電場的作用下與氣體介質發生碰撞電離并運動至陽極,形成陽極吸收電流,從而導致間隙擊穿。因此可將有觸點短路放電的移動電極簡化等效為一維板-板放電模型,如圖1所示。其中v是移動速度,d0是兩電極發生火花放電的初始位置。通過調節電極軸轉速可改變電極移動速度,進而分析速度對移動電極火花放電的影響。

圖1 板-板等效放電模型Fig.1 Plate-to-plate equivalent discharge model
根據電場強度與極板電壓和間隙距離的關系可以推導得出移動電極的場強表達式為
(6)
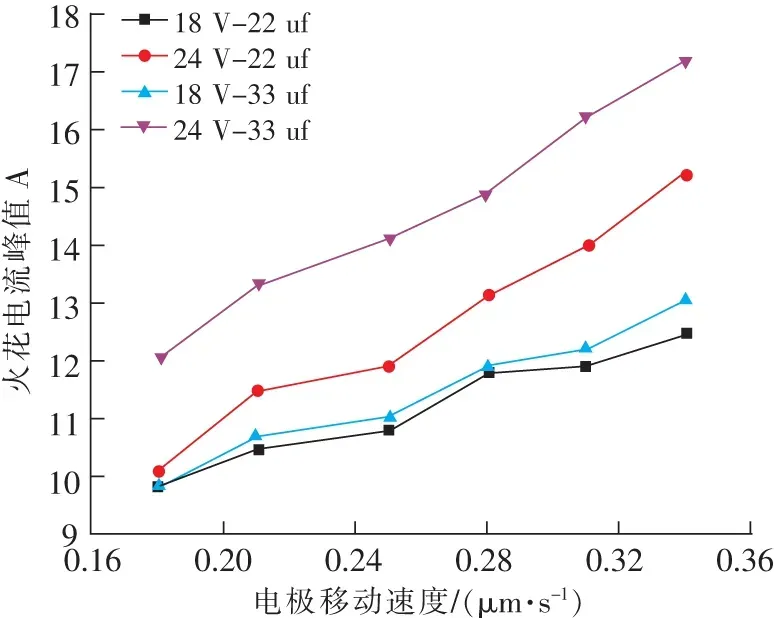
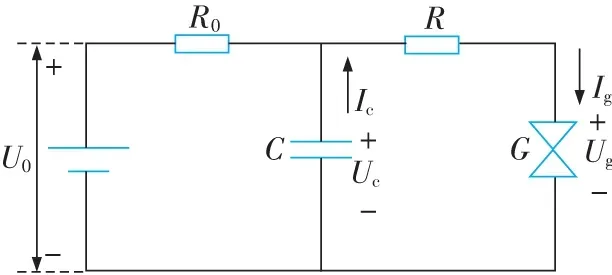
式中β為場增強因子;t為電極的運動時間;vt (7) 根據式(7)得出不同移動速度下lgJ的變化曲線,從圖2可以看出隨著電極移動速度增加,lgJ的值線性增大,即場致發射電流密度J迅速增大。 圖2 電極不同移動速度下的電流密度變化Fig.2 Variation of current density at different moving speeds of electrodes 根據火花試驗放電波形,將火花電壓從初始電壓開始下降至10 V的放電過程,定義為一次放電;將火花電壓從10 V開始下降至0 V的放電過程,定義為二次放電。考慮一次放電是以場致發射為主導的微間隙放電,二次放電是容性電路的無觸點短路放電[22-23]。因此,分析電極移動速度對火花放電的影響時,重點考慮電極移動速度對一次放電特性的影響。 通過改變電極移動速度,測試在不同初始電壓、電容條件下的火花放電特性。從圖3和圖4可以看出:隨著電極移動速度增加,火花電流峰值增大,這與上述理論分析一致。且隨著電極移動速度增加,一次放電時間減小,這是由于在一定間隙距離下,電極移動速度加快,減少兩電極的非接觸時間,即減少微間隙的放電時間。在定電參量條件下,一次放電時間是關于電極移動速度的非線性函數。通過函數擬合得到在初始條件為18 V-22 μf的條件下,一次放電時間T1與電極移動速度v的函數關系為 圖3 不同移動速度下的火花電流峰值Fig.3 Peak of spark current at different moving speeds 圖4 不同移動速度下的放電時間Fig.4 Discharge time at different moving speeds (8) 由于電極移動速度改變火花電流和放電時間的大小,因此需要通過建立模型進一步分析移動速度對火花功率的影響。 根據火花放電實驗平臺,可將其等效為如圖5所示的電路。其中U0為初始電壓;Uc為電容電壓;Ug為火花電壓;Ic為電容放電電流;Ig為火花電流;R0為充電電阻;R為放電回路電阻,其包含線路電阻與火花試驗裝置內阻,R0?R;G為火花試驗裝置。 圖5 電容短路火花放電電路Fig.5 Capacitor short circuit spark discharge circuit diagram 通過分析可以得出一次放電火花電壓按指數函數曲線變化[17],所以另Ug的表達式為 (9) 式中A1和A2為待求解參數。 根據圖5電路所示,得到放電回路的電壓和電流關系式為 Uc=IgR+Ug (10) (11) 將式(10)求微分,代入式(11)。對于火花一次放電時,Ug的初始值為U0,結束值為10 V。所以邊界條件設置為 (12) 將上式代入式(11),即可求得A1,A2的參數值,于是可以得到一次放電t時刻的火花電壓表達式為 (13) 式中T1為一次放電時間,μs。由上式關系,根據Ig的初始值為0,可以得出火花電流的表達式為 (14) 那么推導一次放電的火花功率P1g為 (15) 式中T1為關于電極移動速度v的函數,那么將式(8)代入式(15)即可得到不同移動速度下的火花功率大小。 為分析火花功率與電極移動速度的關系并驗證所建模型的正確性,文中通過調節IEC安全火花試驗裝置的電極軸轉速,以測試移動電極在速度為0.21,0.25,0.28 μm/μs,電壓18 V,電容22 μf,電阻0.26 Ω條件下的火花功率大小。通過示波器(型號為RIGOL DS4024)可以測得移動電極火花電壓、電流曲線,即可得到火花試驗條件下的火花功率大小。把電極的不同移動速度代入式(8),即得到對應的火花放電時間,將該值代入式(15),即得到不同移動速度下火花功率的模型計算值。 通過對比發現模型計算功率反應火花試驗功率的變化趨勢。從圖6可以看出:隨著電極移動速度增加,火花放電的瞬時功率增大。且電極移動速度越快,在越短的時間內越易達到較高功率。這一方面是由于單位時間內場致發射電流密度增大,所引起的放電電流增大,從而使得放電功率增大。另一方面是因為隨著電極移動速度加快,根據Bernoulli方程和流體的連續性方程分析可知放電間隙內的壓強會減小[24-26],即導致間隙內粒子的平均自由程增大,粒子經過少量的碰撞就可到達陽極,所以火花電流的上升速率加快,這也會引起單位時間內火花功率增大。 圖6 火花試驗功率與模型計算功率對比Fig.6 Comparison of spark test power and model calculated power 根據式(15),由火花功率對時間的積分可推導出火花能量的表達式為 (16) 分析γ1,γ2因子隨一次放電時間的變化關系得到一次放電的火花能量極值為 (17) 該能量會引發放電間隙溫度場變化,改變電極間隙的放電情況,增加放電粒子能量。帶電粒子與爆炸性氣體相互作用會產生自由基等活性物質,從而加速爆炸性氣體的化學反應過程。這可為下一步分析火花引燃過程提供參考。 1)隨著電極移動速度增加,單位時間內電場強度增大,電流密度增大,從而一次放電的火花電流增大。 2)在定電參量條件下,一次放電時間隨電極移動速度增加而減小。 3)隨著電極移動速度增加,火花功率增大,且在越短的時間內越易達到較高功率。火花能量與放電時間是非線性的關系,且存在火花能量極值。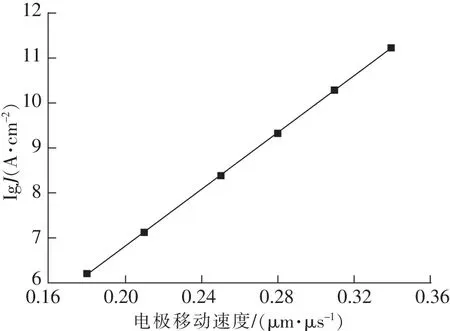

2 移動速度對火花功率的影響
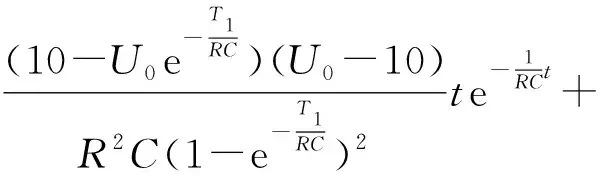
3 實驗驗證及分析

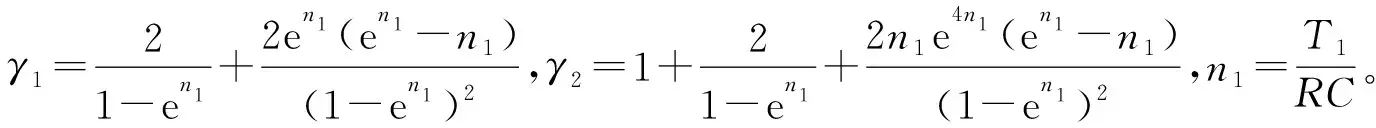
4 結 論

