彈性接觸支撐梁橫向振動動力學建模研究

陳校鋒，朱 翔，李天勻，毛藝達，王春旭

（1.華中科技大學 船舶與海洋工程學院，武漢 430074；2.高新船舶與深海開發裝備協同創新中心，上海 200240；3.船舶與海洋水動力湖北省重點實驗室，武漢 430074；4.中國艦船研究設計中心，武漢 430064）

梁結構在工程中得到廣泛使用，其振動中的非線性通常包括物理非線性、幾何非線性和邊界條件的非線性。對于船舶推進軸系等梁類結構的振動，激振測試表明軸系與船體結構的橫向振動具有強耦合特性，且是接觸耦合，這種接觸耦合一般是非線性的。關于物理或幾何非線性梁的振動已經受到眾多學者的關注。Pielorz[1]分析了懸臂梁在小應變下的大撓度和大轉動時的有限振動，采用伽遼金法求解彈性和黏彈性梁的雙曲或拋物非線性偏微分方程。Barari 等[2]采用變分迭代和參數攝動法研究了軸向載荷作用下Euler-Bernoulli梁的非線性振動，將結果和誤差與四階Runge-Kutta 法的計算結果進行了比較。劉小靖等[3]提出了一種修正小波伽遼金法，用以解決任意強非線性的梁彎曲問題，該方法克服了邊界延拓問題，成功用于求解具有非線性特征的梁的大撓度彎曲問題。賈布裕等[4]考慮了材料的彈塑非線性對計算組合梁的可靠度的影響，結果表明幾何非線性降低了組合梁結構的可靠度值。祖福興等[5]將配點法與徑向基函數相結合，得到了一種適用于求解非線性梁的計算方法。黃正等[6]借助向量式力學的思想，提出了一種新的有限質點法來描述梁的非線性變形。張年梅等[7]研究了受軸向載荷作用的非線性彈性梁的混沌運動，采用Melnikov 法確定系統發生混沌的臨界條件。

典型的邊界條件非線性包括結構構件間的接觸或間隙，各構件間的相互碰撞、分離及摩擦容易引發機械振動和噪聲，導致系統性能下降等一系列問題[8]。目前，已有部分學者針對接觸或間隙邊界條件下非線性梁的振動問題開展了相關的研究。Turner[9]采用多尺度法研究了赫茲接觸邊界條件下懸臂梁的非線性振動問題，通過推導證明了非線性幅頻關系取決于模態數和線性接觸剛度。Sedighi等[10－11]針對死區非線性問題，提出了一種新的有效的精確等效函數，并采用參數展開法研究了存在死區非線性邊界條件懸臂梁的非線性振動。翟國富等[12]對含有非線性赫茲接觸條件的雙梁結構進行了沖擊特性分析，其結果相比于線性模型更能準確地預測接觸系統的耐沖擊能力。相關學者也進行了試驗研究，Praveen 等[13]從實驗和數值兩方面研究了懸臂梁雙側碰撞的振動問題，考慮了接觸剛度、間隙和接觸材料對結果的影響。曹妍妍等[14]同樣以具有間隙約束的懸臂梁為試驗模型，分析了系統在不同激勵參數和接觸剛度下響應狀態隨系統參數的變化規律。萬雨婷等[15]采用掃頻的方式研究了含間隙限位約束梁結構的一階頻響特征，考慮了激勵幅值和間隙大小對結構振動特性的影響。

從以上研究可見，針對梁與彈性支撐在接觸狀態下的研究還相當匱乏，相關研究尚難以揭示梁和彈性支撐在接觸狀態下的非線性動力學特性。本文將彈性梁與支撐彈簧的非線性接觸簡化為用一種分段線性模型表示，通過能量法建立三支撐彈性接觸梁的動力學模型，采用Runge-Kutta法分析模型在簡諧激勵下的動態特性，并討論了激勵參數和支撐剛度對結構非線性振動特性的影響。

1 彈性接觸支撐梁橫向振動動力學模型

考慮三支撐彈性接觸梁模型，模型中假設支撐彈簧只能壓縮而不能伸長，以此來模擬梁和支撐彈簧的接觸行為，如圖1所示。以彈性梁的左端面作為x軸的原點，梁剛接觸彈簧即彈簧無壓縮時的位置為初始位置和z軸的原點。梁的長度為l，橫截面寬為b，厚為h。材料密度為ρ，楊氏模量為E。支撐彈簧分別位于x1、x2、x3處，其剛度分別為k1、k2、k3。在梁的左端x0處作用垂向動態激勵力F。

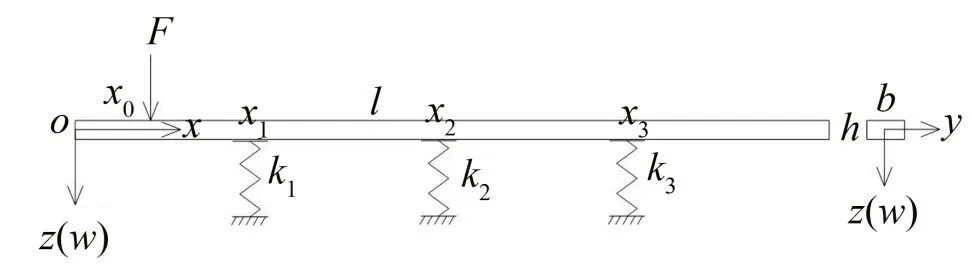
圖1 三支撐彈性接觸梁模型示意圖

為了求解接觸支撐梁在受到激勵后的響應，采用假定振型法來確定接觸支撐梁的運動方程，假設接觸支撐梁的橫向位移為：

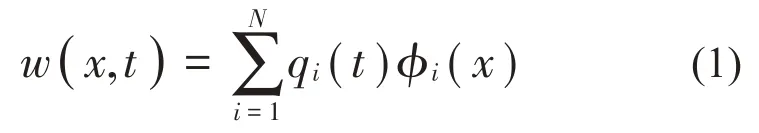
式中的形函數假設為：

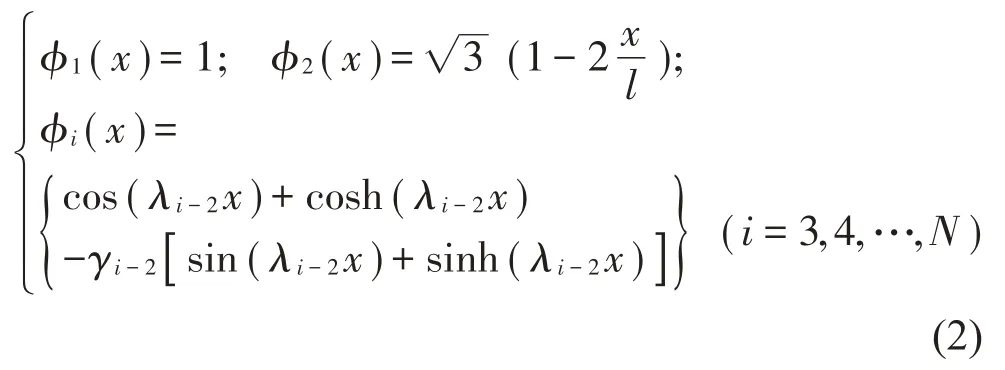
其中：γi-2=且 1-cosλlcoshλl=0，可近似取λi-2=其中形函數的前兩項φ1(x)和φ2(x)為兩端自由梁運動的剛體模態，描述梁垂向的平動和轉動。

假設梁為線彈性材料，則梁的動能和應變能可以分別表示為：

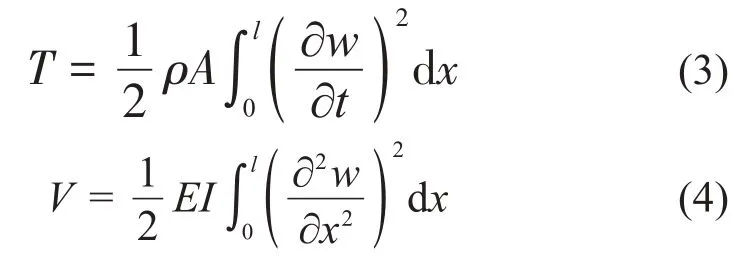
其中：A為橫截面面積，I為慣性矩。忽略支撐彈簧的質量，則其彈性勢能為：

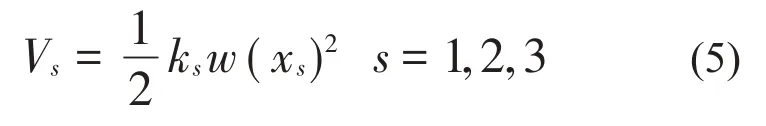
考慮重力的影響，梁的重力勢能為：

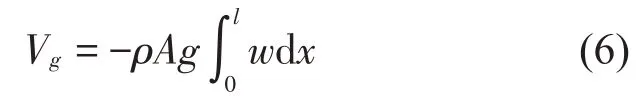
激勵力做功：

根據哈密頓原理：

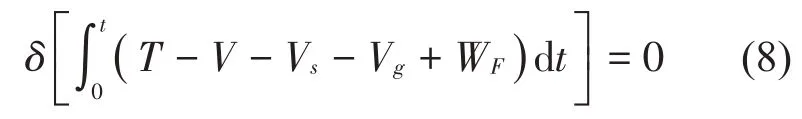
由此得到接觸支撐梁的運動方程為：

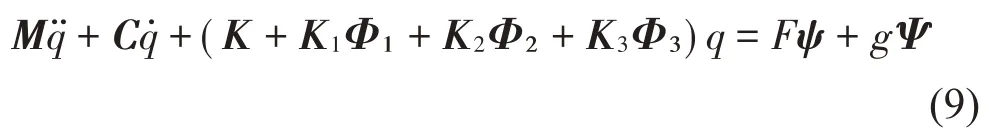
假設系統的阻尼形式為瑞利阻尼，即：

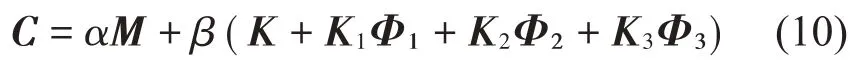
其中：α和β是比例系數，假設彈簧只能壓縮，則：

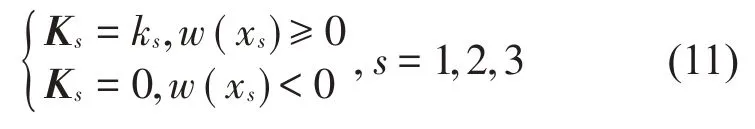
由此可以看出，本文將彈性接觸支撐梁的振動等效為一種分段線性振動。

引入2N維狀態向量p(t)=，則運動方程可寫成1階微分方程組[16]：

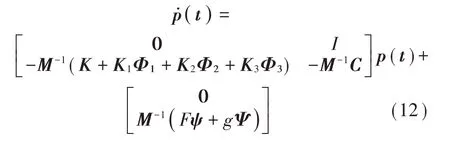
采用經典的4 階Runge-Kutta 法對q(t) 的值進行求解，再代回假定位移的表達式中，即可得到該時刻梁在任意位置處的橫向位移。

當分析模型被簡化為線性模型時，支撐彈簧與梁之間不產生分離，此時可以通過改變梁與彈簧的連接條件，即可得到線性彈簧支撐梁模型，可同樣采用Runge-Kutta法進行時域響應分析，或者采用能量法進行頻域響應分析。

2 算例分析

在算例分析中，取以下參數進行計算：梁的材料密度為ρ=7 850 kg/m3，楊氏模量為E=2.1×1011Pa，梁長l=2 m，寬b=0.05 m，厚h=0.05 m，支撐彈簧的剛度分別為k1=k2=k3=1×106N/m，位置坐標分別為x1=0.5 m，x2=1 m，x3=1.5 m。激勵位置坐標x0=0.2 m，重力加速度g=9.8 m/s2。

形函數的截斷項數N取10，通過對式(9)的求解，得到彈性支撐梁的前3 階固有頻率分別為30.27 Hz、40.52 Hz、75.52 Hz。

根據下式計算瑞利阻尼的比例系數[17]：

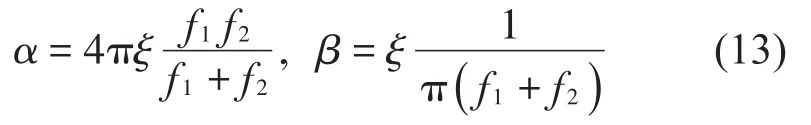
由于主要考慮梁的低頻振動，取f1=10 Hz、f2=100 Hz，阻尼比取ξ=0.03，得到α=3.427 s-1，β=8.681×10-5s。

在x0處施加垂向的簡諧激勵力，激勵幅值為150 N，頻率為10 Hz，進行時域響應分析，分析時長為t=10 s。接觸支撐梁在x1處的響應結果如圖2所示，其中圖2(c)和圖2(d)是根據接觸支撐梁在6 s～10 s時間內的位移及速度響應所繪制的相平面圖和龐加萊截面圖。

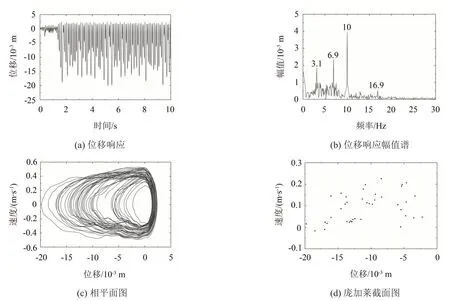
圖2 接觸支撐梁在簡諧激勵下的時域響應(F=150 N，f=10 Hz)

計算結果表明，在該激勵下的梁和彈簧的接觸行為處于接觸(u(xs)≥0)與不接觸(u(xs)＜0)交替進行的狀態。位移響應幅值譜的峰值頻率點中并沒有出現彈性支撐梁的固有頻率點，而是出現了非線性振動中所特有的超諧波共振和次諧波共振。從相平面圖和龐加萊截面圖則可以更明顯地看出接觸支撐梁的響應不是簡單的周期或準周期運動，而是一種有界的不規則的穩態運動形式，說明彈性接觸支撐梁的運動是非線性振動。

3 驗證分析

3.1 有限元模型

為了驗證本文計算方法的正確性，采用了有限元分析軟件ANSYS 對三支撐彈性接觸梁進行建模分析。彈性梁采用BEAM188 梁單元模擬。進行模態分析時，不考慮梁與彈簧的接觸行為，即支撐梁模型的彈簧采用COMBIN14彈簧單元模擬；進行時域響應分析時考慮接觸的情況，即接觸支撐梁模型的彈簧采用COMBIN40彈簧單元模擬，該單元的物理模型如圖3所示。

圖3中的GAP 表示間隙的大小，當u(J)-u(I)+GAP≥0 時，間隙打開，此時彈簧不受力，當u(J)-u(I)+GAP＜0時，間隙閉合，彈簧受壓。在本文中，可將GAP設置為一個足夠小的小量，用以模擬梁和彈簧的接觸行為。設置梁單元的大小并劃分網格，約束彈簧下端點處的所有位移，得到接觸支撐梁的有限元模型，如圖4所示。

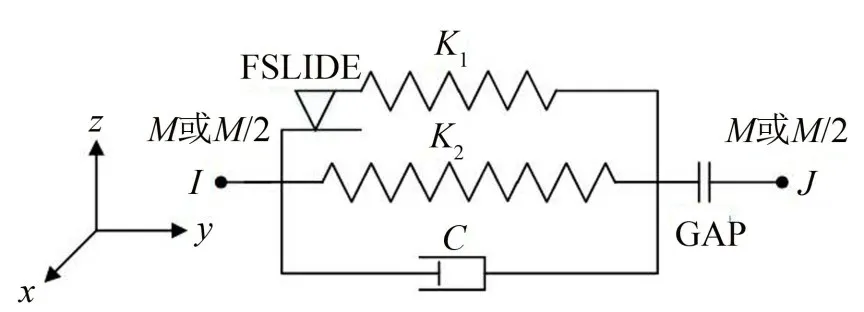
圖3 COMBIN40單元

圖4 三支撐彈性接觸梁有限元模型

3.2 結果對比

當不考慮梁與彈簧的接觸行為時，計算彈性支撐梁的固有頻率，如表1所示。可以看出，在形函數的截斷項數N=10 時，本文的求解結果已經收斂，且前5 階固有頻率與有限元結果的誤差均在1.5%以內，說明形函數取N=10進行計算分析是較為準確可靠的。

表1 彈性支撐梁的固有頻率/Hz

考慮梁與彈簧的接觸行為，對彈性接觸支撐梁有限元模型施加激勵幅值為150 N，頻率為10 Hz的簡諧激勵，選用Newmark-β直接計算法進行瞬態分析，對比本文和有限元的計算結果，如圖5所示。可以看出兩種方法的計算結果吻合較好，表明本文所采用的計算方法是可行的，準確的。

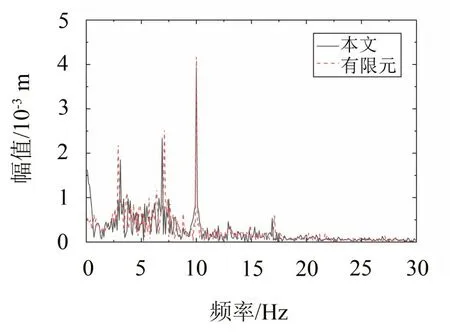
圖5 彈性接觸支撐梁時域響應結果對比(x1處的位移幅值譜)

4 參數討論

對于非線性系統，其初始狀態對振動的特性有較大影響。尤其是當系統進入混沌后，系統對初始值十分敏感，即初值的微小擾動會使系統的長期運動發生很大變化，其運動是一種有界的不規則的穩態運動[18]。其中有界是指混沌運動的狀態變量(如：位移、速度)是在某個區間內變動的，不規則指的是其運動軌跡沒有規律可循，類似于隨機運動。本節通過分岔圖研究彈性接觸支撐梁系統中所施加激振力的幅值、頻率和彈簧剛度對接觸支撐梁運動狀態的影響。分岔圖是由狀態變量和分岔參數所構成的圖形空間，表示狀態變量隨參數的變化。

以接觸支撐梁在支撐位置x1處的位移作為狀態變量，激勵力的幅值作為分岔參數繪制接觸支撐梁關于激勵幅值的分岔圖，如圖6所示。其中，激勵頻率為10 Hz，激勵幅值的變化范圍是50 N～300 N。在F＜138 N 時，分岔圖表現為1 條隨激勵幅值變化的曲線，表明接觸支撐梁在該激勵下的運動為周期運動。當F≥138 N時，其運動狀態突然改變，進入了混沌運動，在分岔圖上表現為一個分岔參數對應無限個狀態變量點。運動狀態的突然改變可能是因為激勵幅值增大到一定的值，梁和彈簧的接觸行為一直處于接觸與不接觸交替進行的狀態，從而進入了混沌。而激勵幅值小于這個值時，梁和彈簧最終會處于接觸的狀態，不再分離，此時結構為線性系統，故梁的運動為周期運動。

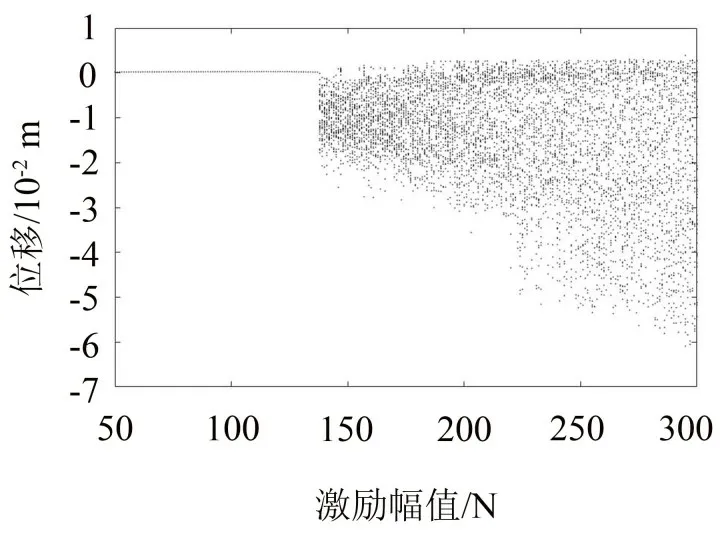
圖6 接觸支撐梁關于激勵幅值的分岔圖

固定激勵力幅值為200 N，以x1處的位移作為狀態變量繪制分岔圖，激勵的頻率范圍為10 Hz～100 Hz，如圖7所示。分岔圖中某個分岔參數下的狀態變量為有限個(k個)孤立點，可以表示系統在該分岔參數下的周期k運動[18]。從圖7可見，接觸支撐梁在激勵頻率f小于76.5 Hz的大部分區間內均作混沌運動，而在46 Hz～48 Hz 和60 Hz～68 Hz 之間，接觸支撐梁分別發生了周期2和周期1運動。最后，接觸支撐梁的振動大約在77 Hz處從混沌運動轉為周期2運動，并在79.5 Hz處進入周期1運動。此外，隨著激勵頻率的增大，狀態變量的變化區間呈現減小的趨勢。因此，當激勵頻率較低時，接觸支撐梁的運動更有可能進入混沌運動。

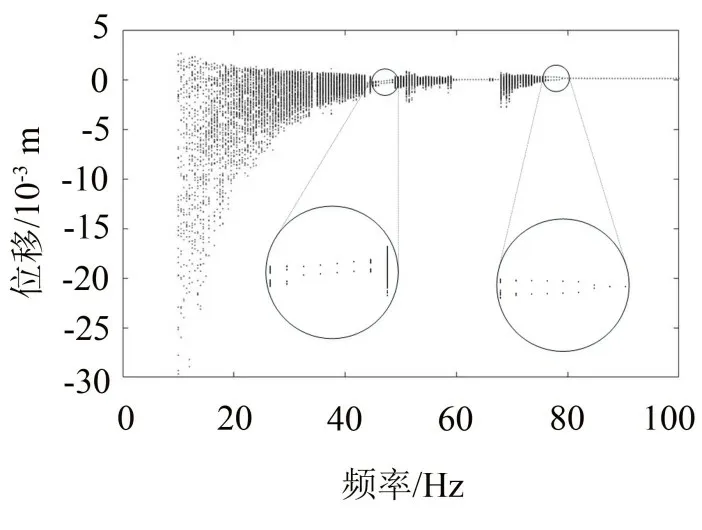
圖7 接觸支撐梁關于激勵頻率的分岔圖

改變支撐彈簧k1的剛度系數，令F=150 N，f=10 Hz，以x1處的速度作為狀態變量繪制分岔圖，如圖8所示。在彈簧剛度k1小于1.3×107N/m的區間內，接觸支撐梁作混沌運動，但在[0.66,0.8]×107N/m 的區間內則突然變為周期1運動。之后便進入了周期運動，其中在約1.64×107N/m處進入周期2運動，并最終在3.3×107N/m處重新進入周期1運動。這說明了支撐彈簧的剛度系數對接觸支撐梁的振動狀態也會產生較大的影響。

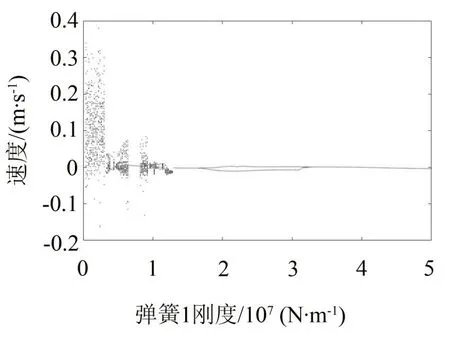
圖8 接觸支撐梁關于彈簧剛度k1的分岔圖

5 結語

工程中某些情況下梁和彈性支撐之間并不是理想的線性耦合關系，本文考慮了彈性梁與支撐彈簧之間的接觸行為，假設梁的支撐彈簧僅能承受壓縮，探討非線性邊界條件對接觸支撐梁的振動特性的影響。建立了三支撐彈性接觸梁的分段線性動力學模型，采用Runge-Kutta法求解結構在簡諧激勵下的動態特性。通過與有限元軟件的仿真結果對比，驗證了該方法的有效性。

本文還討論了激勵參數和彈簧剛度系數對接觸支撐梁非線性振動特性的影響。結果表明，激勵幅值較大或激勵頻率較低時，都有可能會使接觸支撐梁的振動從周期運動進入混沌運動，彈簧剛度系數也會對接觸支撐梁的振動狀態產生一定的影響。得到彈性接觸支撐梁在不同參數下的振動特性后，可以通過合理的結構參數設計來避免系統進入混沌等不穩定的振動狀態，以上研究可為梁類結構的振動控制提供參考。