變頻空調壓縮機電機的振動噪聲優化研究

張德金 江波 邱小華

廣東美芝制冷設備有限公司 廣東順德 538333

0 引言

隨著國家空調能效等級要求的不斷提升，變頻壓縮機以其高效特性、結構緊湊的優勢在市場上的占有率逐年提升。但隨著市場競爭的加劇，在1～3 HP家用空調領域，分布式繞組變頻電機逐漸被集中式繞組電機取代，雖然集中式繞組電機較分布式繞組電機有更低的成本優勢和更高的性價比，但其噪聲問題較分布式變頻電機更為嚴重。隨著人們對家用電器噪聲舒適性的要求越來越高，變頻壓縮機電機的噪聲優化愈來愈受到重視[1]。

在噪聲改善上，得益于計算技術的發展，有限元+電機優化算法+多物理場耦合分析已廣泛應用于電機優化設計上[2-3]，但傳統拓撲結構的設計優化效果變得有限。另一方面，基于磁場調制原理的新結構電機成為近年研究熱點[4-7]，磁齒輪電機、永磁游標電機、無刷雙饋電機是新原理電機的典型代表，但上述研究的新結構目前主要應用于直線電機、風力發電機等，與空壓的傳統應用結構相結合的難度大。

本文基于以上的前沿研究與空調壓縮機的應用背景，首先分析指出轉子勵磁諧波和定子激磁諧波是導致電磁激振力的主要來源，通過對徑向、切向磁密進行對比分析，發現徑向力密度是導致壓縮機振動噪聲的主要因素，并通過有限元進行力密度的時空階次分析計算，結合壓縮機的噪聲頻譜，得出分析電機電磁力的有效計算方法，為后續壓縮機的噪聲改善提供可靠的分析工具。

1 壓縮機的電磁激勵

根據麥克斯韋張量法計算作用于定子鐵芯結構的徑向、切向電磁激振力密度為：

式中，br和bt分別為氣隙磁密的徑向和切向分量；μ0為真空磁導率，μ0=4π×10-7H/m。

本文所分析的集中式繞組電機定子槽數Q1=9，轉子極對數p=3，則每極每相槽數為：

式中，q'和d互質。

氣隙磁密中定子側和轉子側產生的諧波次數分別為：

式中，ν和u分別為定子側和轉子側的氣隙磁密諧波次數；m為相數。再加上定子開槽和轉子削弧結構設計，氣隙磁場中含有非常復雜的各類諧波。

由于定子諧波和轉子諧波相互作用，產生了除基波轉矩之外的徑向電磁激振力和切向電磁激振力，切向電磁激振力可以引起轉矩波動，而徑向電磁激振力是產生振動噪聲的主要因素。

定轉子的氣隙磁密諧波相互作用產生的電磁力波階數和相應的頻率為：

式中，r為力波階數；fr為力波激振頻率；f為電機電頻率。當定子諧波和轉子諧波階次較為接近時，可產生力波階次較小的力密度。

2 激振力和壓縮機噪聲頻譜分析

2.1 定轉子激勵磁密波形

2.1.1 不考慮磁導影響的磁密波形

在永磁電機中，氣隙主磁場主要通過轉子永磁體勵磁，并與定子繞組電流激發旋轉磁場相互反應輸出轉矩，其中轉子勵磁磁密波形和諧波分析如圖1所示，定子激磁磁密波形和諧波分析如圖2所示。

由圖1可知，由轉子磁鐵激勵出的氣隙磁場諧波含量主要為1（基波）、3、5……等階次，與解析計算吻合。在轉子激勵的磁場中，諧波主要為奇次諧波，與解析計算吻合。

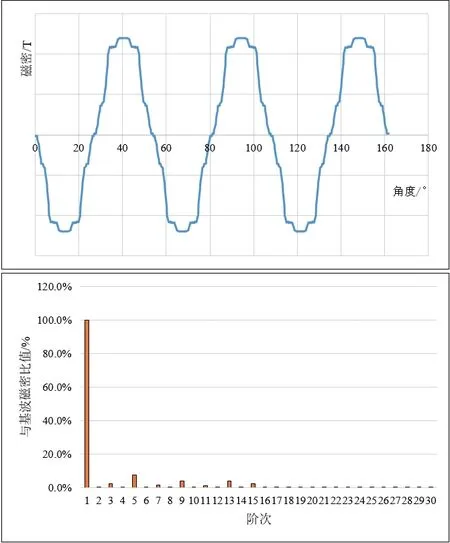
圖1 不考慮磁導的轉子勵磁磁密波形和諧波分析

由圖2可知，由定子繞組激勵出的氣隙磁場諧波含量主要為1（基波）、2、4、5……等階次，與解析計算吻合。

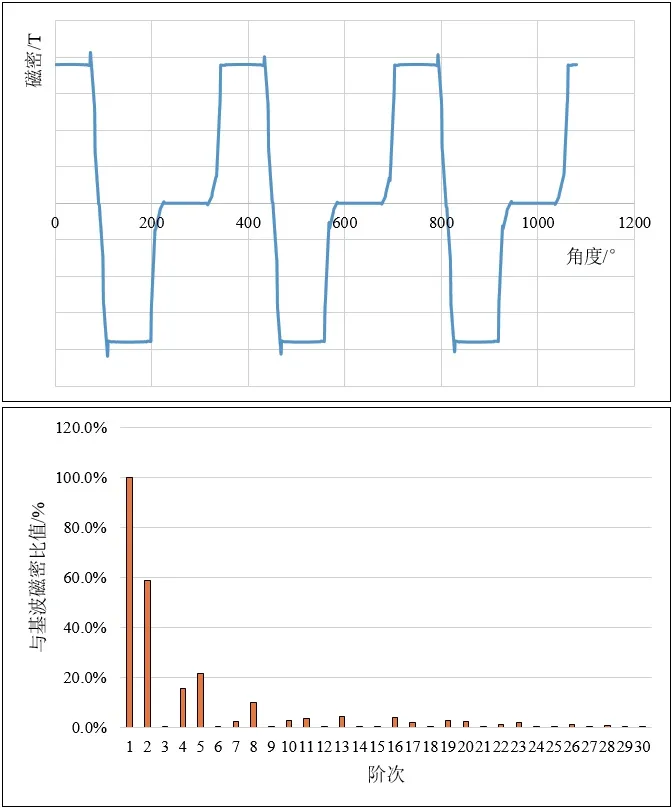
圖2 不考慮磁導的定子激磁磁密波形和諧波分析

2.1.2 考慮磁導影響的磁密波形

由于定子的開槽和轉子的削弧設計，導致在氣隙磁場中的磁密諧波引入和磁導因素影響，其對轉子勵磁和定子激磁的影響如圖3和圖4所示。

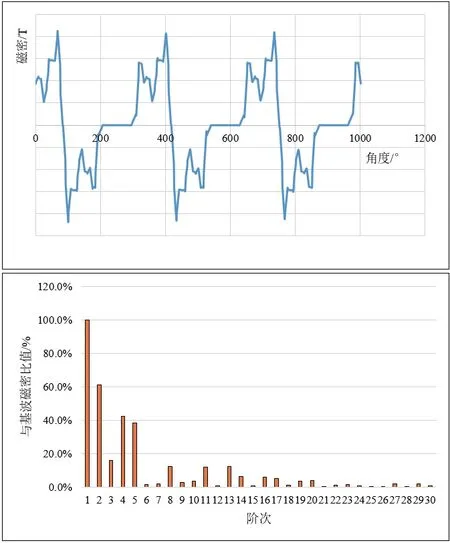
圖4 考慮磁導的定子激磁磁密波形和諧波分析

由圖3可知，在考慮磁導后，轉子磁鐵激發出的氣隙磁密波形中諧波成分與不考慮磁導時不同，增加了偶次諧波，且部分奇次諧波含量被降低。

圖3 考慮磁導的轉子勵磁磁密波形和諧波分析

由圖4可知，在考慮磁導后，定子繞組激勵出的氣隙磁密波形中諧波成分與不考慮磁導時較為接近，3的倍數次諧波幾乎近似于無。

由上述所知，理論解析推導的定轉子激勵諧波次數為不考慮磁導的情形，即不考慮定子開槽和轉子的削弧，這與實際情況不符。因此，在進一步分析由諧波交互產生的諧波激振力時，應主要考慮磁導的磁密波形分析結果。

2.2 力密度波形

根據Ansoft Maxwell仿真計算軟件計算額定工況下的電機氣隙磁密，其中徑向和切向氣隙磁密波形如圖5所示。

由圖5可知，徑向磁密的幅值遠遠大于切向磁密幅值，徑向磁密的幅值可達1.0～1.1 T，而切向磁密的幅值僅0.1 T左右。由公式（1）和（2）可知，徑向激振力密度遠遠大于切向激振力密度，因此，后續進行力波分析時，僅分析徑向激振力密度。

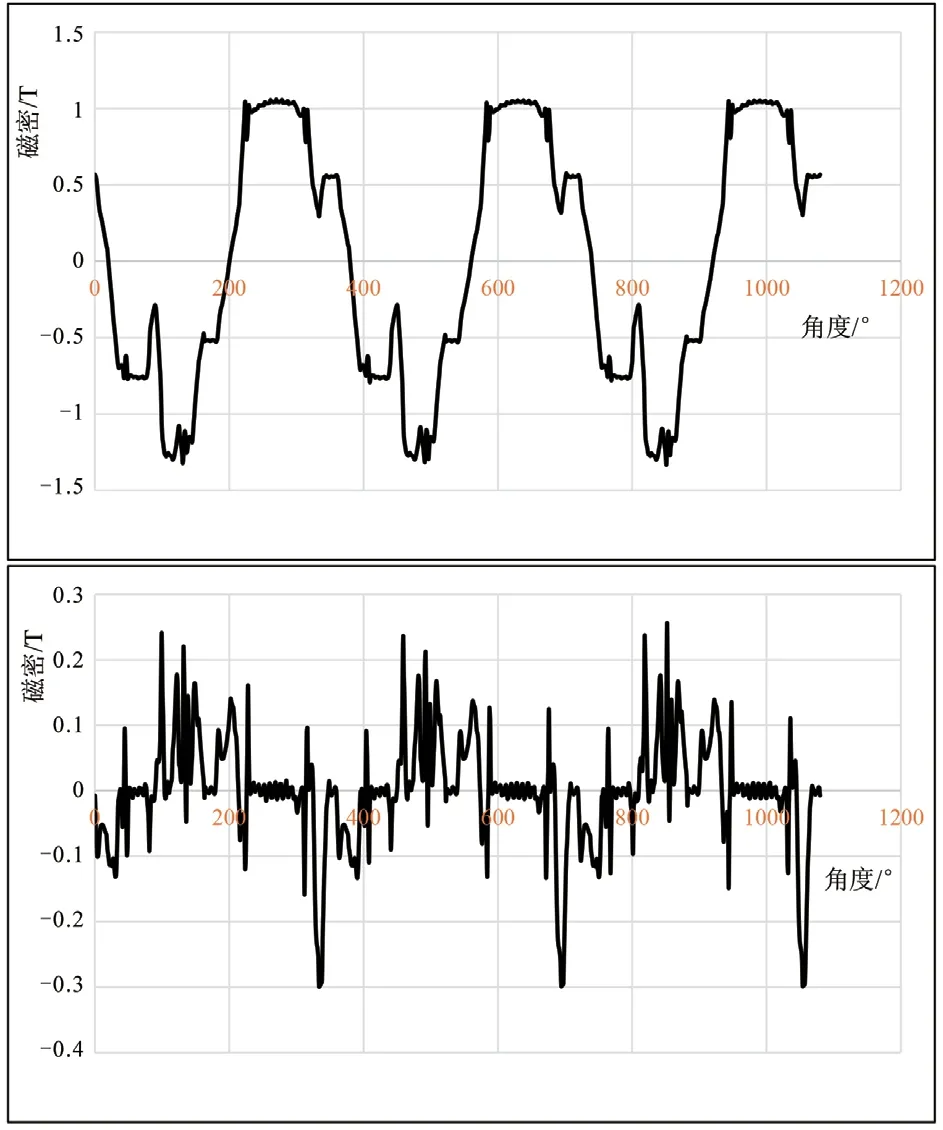
圖5 運轉時電機氣隙徑向和切向磁密

根據公式（1）對磁密數據進行后處理，計算在t=0時刻下的徑向激振力密度，其波形如圖6所示。

由圖6可知，對6極電機空間磁密進行力密度計算后，激振力密度有6個峰值，即可視為有6個周期數據，其和轉子極數相對應。

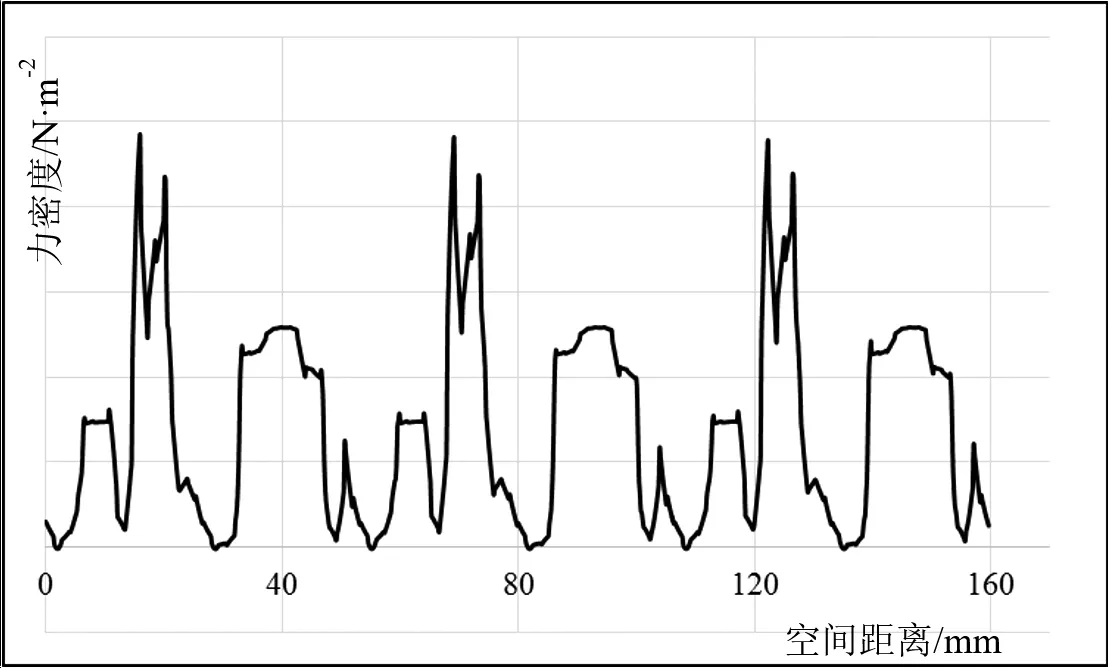
圖6 徑向磁密激振力密度空間波形

取氣隙中靠近定子齒的一點，按照時間分量取其徑向、切向磁密分量，并根據公式（1）計算其激振力密度如圖7所示。由圖7可知，激振力的時間波形上也有6個周期數據，同空間波形一致。

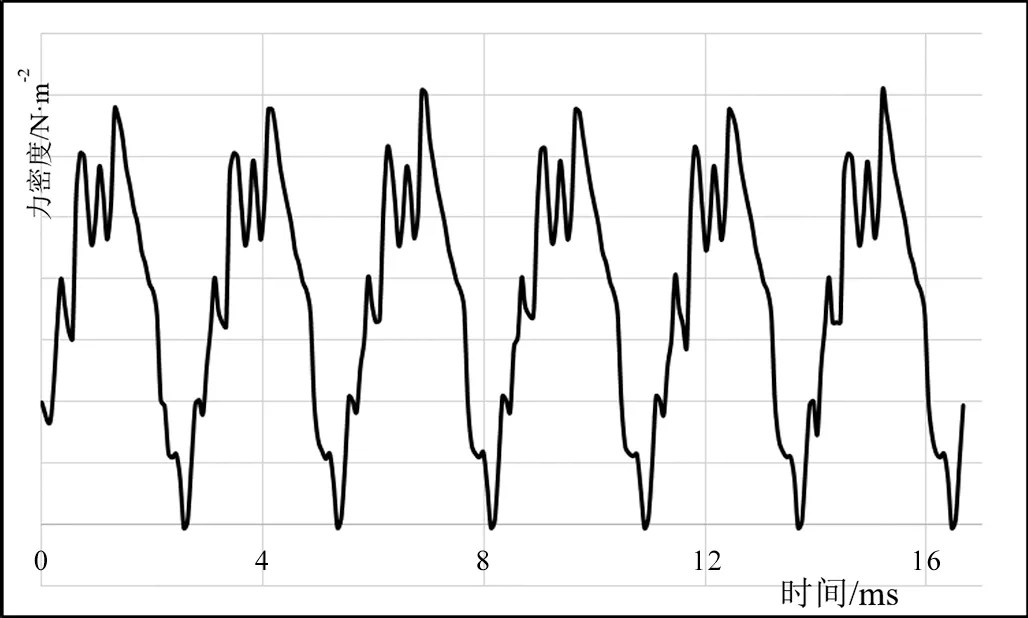
圖7 徑向磁密激振力密度時間波形

根據力波計算，電機氣隙側力密度在轉子旋轉一周的時間內，空間和時間的維度均有周期性的力密度變化，因此根據靠近定子內徑處整圓的不同時間下的氣隙磁密波形，進行時間和空間的二維傅里葉變換，其時空柱形圖如圖8所示。

由圖8可知，激振力密度的0階和3階的幅值較大，對電機噪聲振動的影響較大，其中0階的力密幅值又遠大于3階，因此后文主要分析0階力密對噪聲頻譜的影響。

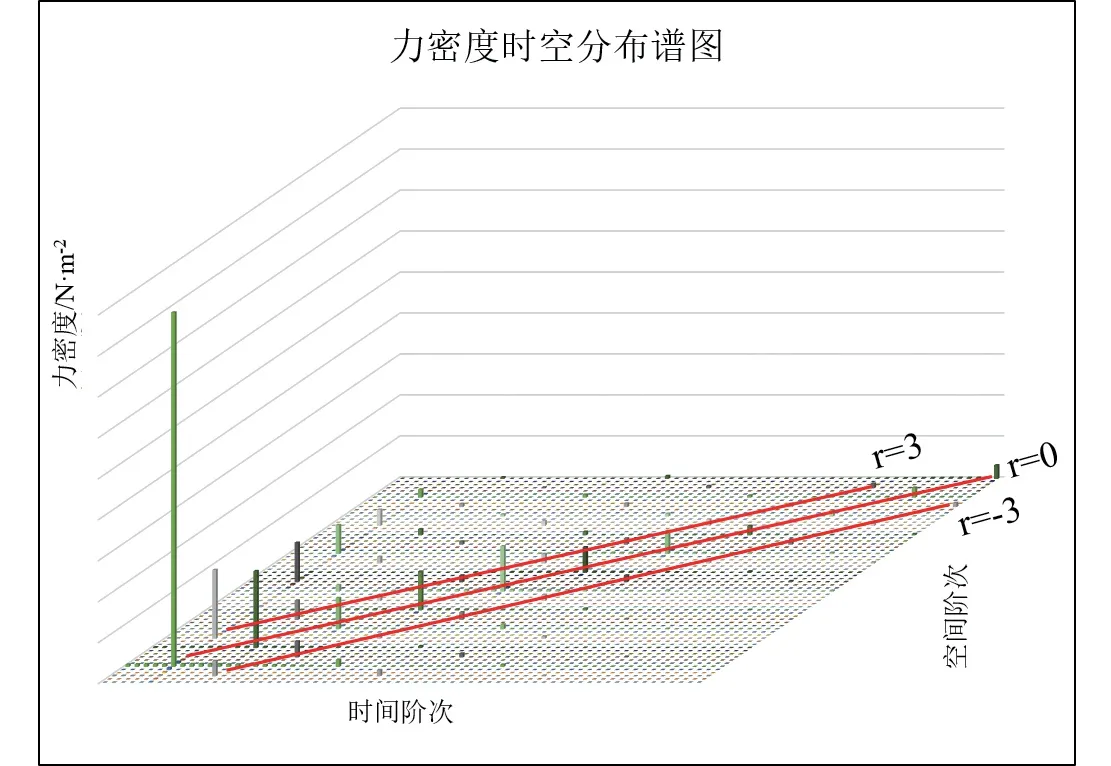
圖8 徑向磁密激振力密度時空分布譜圖

2.3 力密度與噪聲頻譜分析

依據上述理論分析，對新平臺電機開發過程中的式樣進行激振力密度和壓縮機噪聲頻譜的分析，根據輔助計算工具Maxwell仿真計算基準和新方案式樣的激振力密度，并進行二維時空傅里葉變換，其各階次的力密度幅值如圖9所示。

圖9 力密度對比

新方案與基準的頻譜如圖10所示，新方案較基準在60 r/s下的1000 Hz和4000 Hz惡化，在90 r/s下的2500 Hz有惡化。在90 r/s下，新方案力密度的2160 Hz、2700 Hz和3240 Hz較基準增加，頻譜對比為2000 Hz～3150 Hz有不同程度惡化。60 r/s下的4000 Hz惡化和3960 Hz下的力密度增加相對應，1000 Hz較基準惡化嚴重，但力密度基本一致，推測為泵體的變化帶來的排氣噪聲惡化。

綜上所述，理論仿真分析的力密度變化與壓縮機噪聲頻譜基本吻合，可以確定該分析過程的正確性和設計指導意義。

3 結論

通過對電機激振力的產生機理進行理論推導和分析，結合Maxwell仿真計算工具得出定子側和轉子側激磁產生的磁密諧波，并分析其分布特征。氣隙中徑向磁密遠大于切向磁密，所以電機的激振力主要由徑向磁密激發。由于磁導的激發分化，氣隙磁場中的徑向磁密諧波含量豐富，定子繞組側主要有2、3、4、5、8、11等階次諧波；轉子側主要有4、5、7、8、10等階次諧波。

定轉子的諧波相互作用產生階次較低的激振力，當激振力與零部件固有頻率較為接近時，會激發出較大的振動響應，表現為響應頻段的噪聲頻譜惡化。根據解析推導，激振力的頻率為固定離散的點，從激勵側盡可能降低激振力或激振力密度是改善噪聲振動的重要手段。通過分析不同轉子結構下的力密度頻譜和對應結構下的噪聲頻譜，驗證了本文所采用分析方法的正確性，為后續電機沖片設計和噪聲優化提供有效的分析手段和結構借鑒。