一個新三維混沌電路設(shè)計及其同步控制*

閆少輝，施萬林，宋震龍，王爾童，孫 溪，黃羿博

(1.西北師范大學物理與電子工程學院，甘肅 蘭州 730070; 2.甘肅省智能信息技術(shù)與應用工程研究中心，甘肅 蘭州 730070)

1 引言

自1963年氣象學家Lorenz[1]發(fā)現(xiàn)了第一個混沌吸引子以來，混沌理論的研究和應用在非線性科學領(lǐng)域獲得了極大發(fā)展。混沌可以由非線性微分方程的簡單數(shù)學模型產(chǎn)生，其不可預測性和高度偽隨機性等特性使其在保密通信中得到了廣泛應用[2,3]。因此，設(shè)計和實現(xiàn)具有理想特性的混沌系統(tǒng)具有非常重要的理論價值和實踐意義。

在Lorenz系統(tǒng)的基礎(chǔ)上，國內(nèi)外研究人員相繼提出了一系列新的混沌系統(tǒng)。例如，陳關(guān)榮教授發(fā)現(xiàn)的Chen系統(tǒng)具有與Lorenz類似但拓撲不等價的新型混沌吸引子[4]；2002年，呂金虎等人[5]提出了Lorenz系統(tǒng)與Chen系統(tǒng)之間的臨界系統(tǒng)，并將其命名為Lü系統(tǒng)。近年來，在上述系統(tǒng)的基礎(chǔ)上也有許多新的混沌系統(tǒng)不斷被提出。文獻[6]提出了一個新的三維自治混沌系統(tǒng)，該系統(tǒng)方程包含多個非線性項，而在物理實現(xiàn)中，二次非線性和常數(shù)項需要乘法器和直流偏置電壓來實現(xiàn)，使得電路變得復雜。文獻[7]提出了一個三維連續(xù)混沌系統(tǒng)，該系統(tǒng)在x-y平面上的吸引子與Lü系統(tǒng)的相同，其吸引子關(guān)于z軸對稱。因此，設(shè)計電路簡單但動力學行為復雜的混沌系統(tǒng)成為了當前的研究重點。

混沌保密通信一直以來都是非線性科學領(lǐng)域研究的熱點，而混沌同步是實現(xiàn)混沌保密通信的關(guān)鍵。近年來，人們相繼提出了一系列混沌同步控制方法。文獻[8]在新構(gòu)建的四維超混沌系統(tǒng)和四維超混沌Chen系統(tǒng)之間設(shè)計了廣義同步控制器，從而實現(xiàn)了廣義同步。文獻[9]應用主動控制同步法和自適應控制同步法來設(shè)計各自不同的控制器，使得響應系統(tǒng)和驅(qū)動系統(tǒng)達到同步。文獻[10]利用自適應控制方法實現(xiàn)了衍生系統(tǒng)之間的同步以及非衍生系統(tǒng)之間的同步。盡管上述文獻都較好地實現(xiàn)了系統(tǒng)之間的同步，但也導致系統(tǒng)結(jié)構(gòu)更復雜，電路實現(xiàn)更困難。因此，簡化電路結(jié)構(gòu)，研究控制精確且規(guī)則限制少的同步方法將變得尤為重要。

本文基于Bao系統(tǒng)[11]構(gòu)建一個新的三維混沌系統(tǒng)。不同于經(jīng)典Bao系統(tǒng)，新系統(tǒng)產(chǎn)生的混沌吸引子均不對稱，系統(tǒng)具有更復雜無序的混沌特性和新的拓撲結(jié)構(gòu)。通過對該系統(tǒng)的動力學特性研究，結(jié)合不同參數(shù)下的Lyapunov指數(shù)譜和分岔，分析不同參數(shù)對該混沌系統(tǒng)的影響，證明該系統(tǒng)具有豐富的混沌特性。此外，通過計算譜商SE(Spectral Entropy)復雜度和C0復雜度，為電路參數(shù)配置提供了一種直觀有效的方法。同時，在Multisim軟件上對系統(tǒng)電路進行設(shè)計與仿真，實驗結(jié)果與數(shù)值仿真結(jié)果相一致。最后，通過非線性反饋與線性反饋同步控制方法分別實現(xiàn)系統(tǒng)的同步，數(shù)值仿真與電路仿真結(jié)果驗證了系統(tǒng)的可行性。

2 新系統(tǒng)模型與動力學特性分析

2.1 新混沌系統(tǒng)模型

本文根據(jù)Lü系統(tǒng)和Liu系統(tǒng)[5]的構(gòu)建模式，在Bao系統(tǒng)的基礎(chǔ)上構(gòu)建一個新的三維混沌系統(tǒng)。新混沌系統(tǒng)的數(shù)學模型如式(1)所示：

(1)

其中，a，b，c，d為系統(tǒng)參數(shù)。當選取系統(tǒng)參數(shù)a=20，b=14，c=11，d=5，變量x,y,z的初始值為 (1，1，1)時，利用Matlab對混沌吸引子進行了數(shù)值模擬。時間步長設(shè)置為0.01 s，時間長度設(shè)置為50 s。圖1a為三維空間吸引子及其在不同平面上的投影圖。由圖1a可見，系統(tǒng)(1)的吸引子軌跡關(guān)于坐標軸均不對稱，并且其軌跡在特定區(qū)域存在遍歷性[12]，說明該系統(tǒng)具有新的拓撲結(jié)構(gòu)。圖1b為3個變量的時間序列，其時域波形都是非周期的。圖1c為系統(tǒng)在y=0上的Poincare截面，其軌跡為一條沒有閉合的線段且具有自相似的分形結(jié)構(gòu)[13]，說明系統(tǒng)是混沌振蕩的。通過0-1測試，得到呈不規(guī)則分布的p-s運動軌跡,如圖1d所示，計算可得漸近增長率K的值為0.996 3 (K≈1)，表明系統(tǒng)具有混沌特性。

Figure 1 Dynamic behavior of the new chaotic system圖1 新混沌系統(tǒng)的動力學行為

2.2 耗散性與平衡點穩(wěn)定性分析

對于構(gòu)建的新系統(tǒng) (1)，有如式(2)所示的等式：

(2)

其中，V表示相位體積，當a=20，b=14，c=11，d=5時，divV=-a+c-d=-14<0，所以系統(tǒng)是耗散的，并且以指數(shù)形式 dV/dt=e-14t收斂 ，即當t→∞時，系統(tǒng)軌道的所有體積元都會以指數(shù)e-14收縮到0。因此，相空間軌線經(jīng)過多次折疊和拉伸其運動軌跡最終會固定在一個吸引子上，說明吸引子是存在的。

令非線性系統(tǒng)模型(1)的右邊等于0，如式(3)所示：

(3)

求解式(3)，可得系統(tǒng)有3個平衡點：P0=(0,0,0),P1=(12.155,-15.470,35.714)和P2=(-9.069,11.542,35.714)。系統(tǒng) (1)在平衡點P0處的雅可比矩陣如式(4)所示：

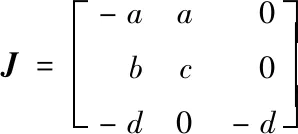
(4)

由此可以推導出特征方程如式(5)所示：

P0(λ)=λ[(a+λ)(c-λ)+db](d+λ)=0

(5)

當選取參數(shù)a=20，b=14，c=11，d=5時，由式(5)可得，系統(tǒng) (1)在平衡點P0=(0,0,0)處的特征根為：λ11=-5，λ12=18.309，λ13=-27.308。由于特征值λ11和λ13為負實數(shù)，λ12為正實數(shù)，這種具有2個穩(wěn)定流形和1個不穩(wěn)定流形的匯合點稱為鞍點[14]，因此P0是一個在二維空間中不穩(wěn)定的鞍點。

將系統(tǒng)在平衡點P1處線性化，其雅可比矩陣如式(6)所示：

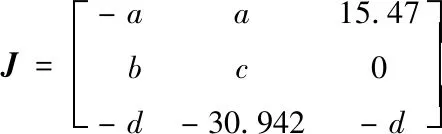
(6)

令det(J-λE)=0，解其特征根為：λ21=-30.2,λ22，23=8.1±6.74i。由于λ21為負實數(shù)，且λ22和λ23均是實部為正的共軛復數(shù)，因此平衡點P1為不穩(wěn)定的鞍焦點。同理，在平衡點P2處，求其特征根為：λ31=-31.9,λ32=4.3,λ33=13.61。由于特征值λ31為負實數(shù)，λ32和λ33為正實數(shù)，因此平衡點P2為不穩(wěn)定的鞍點。

2.3 系統(tǒng)參數(shù)對動力學特性的影響

隨著系統(tǒng)參數(shù)的變化，系統(tǒng)將處于不同的混沌狀態(tài)并呈現(xiàn)出不同的動力學行為[15]。固定系統(tǒng)參數(shù)a=20，b=14，d=5，變量x,y,z初始值設(shè)為 (1，1，1)，選取系統(tǒng)參數(shù)c作為分岔參數(shù)，當c在 (4，16)內(nèi)變化時，系統(tǒng)(1)的Lyapunov指數(shù)譜和關(guān)于變量x的分岔情況如圖2所示，其中，L1，L2和L3為Lyapunov指數(shù)譜。

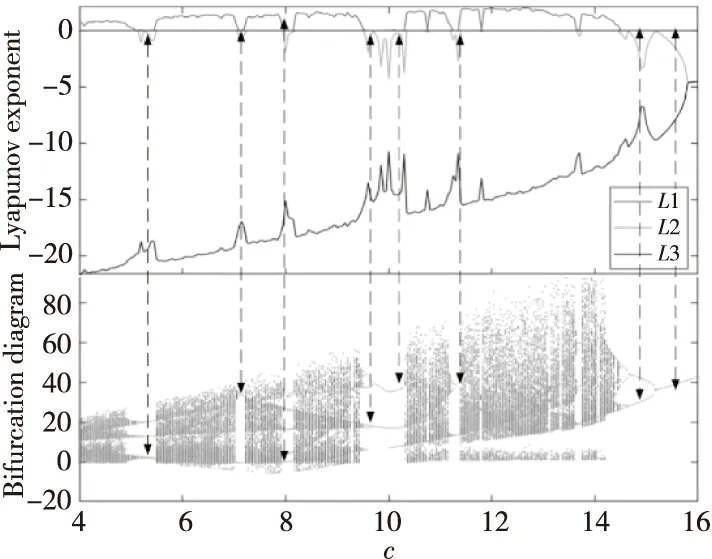
Figure 2 Lyapunov exponent and bifurcation diagram with parameter c varying in the range of (4,16)圖2 參數(shù)c在(4，16)內(nèi)變化的Lyapunov指數(shù)譜與分岔圖

由圖2可見，系統(tǒng)存在著各種脫離混沌的分岔路徑，在路徑中存在混沌與周期的復雜交替，但混沌帶中依然夾有一些周期窗口。當c在 (4，16)內(nèi)變化時，系統(tǒng)從倍周期開始脫離混沌。同時，參數(shù)c取不同值時的吸引子相圖如圖3所示，當c=15時，系統(tǒng)為極限環(huán)，當c=14.8時，系統(tǒng)為二周期，當c=14.6時，系統(tǒng)為四周期，當c=14時，系統(tǒng)為混沌振蕩。此時系統(tǒng)的最大Lyapunov指數(shù)大于0。

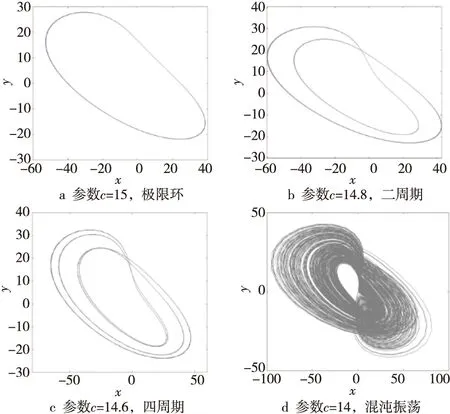
Figure 3 Attractor phase diagram with different values of parameter c 圖3 參數(shù)c取不同值時的吸引子相圖

固定系統(tǒng)參數(shù)a=20，b=14，c=11，變量x,y,z初始值為 (1，1，1)，選擇d作為分岔參數(shù)，當d在(0，12)內(nèi)變化時，圖4給出了變量x對應的Lyapunov指數(shù)譜與分岔圖。由圖4可見，該系統(tǒng)的軌道在這一部分有很多不同的周期和混沌跳躍，并且系統(tǒng)也是從倍周期開始脫離混沌，說明 Lyapunov指數(shù)譜和分岔圖有較好的一致性。此外，圖5顯示了吸引子的相圖，詳細展示了從周期到混沌的演化過程。當d分別取6，8.6，9.6和10時，系統(tǒng) (1)從混沌振蕩(圖5a)開始，到四周期振蕩(圖5b)，到二周期振蕩(圖5c)，再到極限環(huán)(圖5d)。

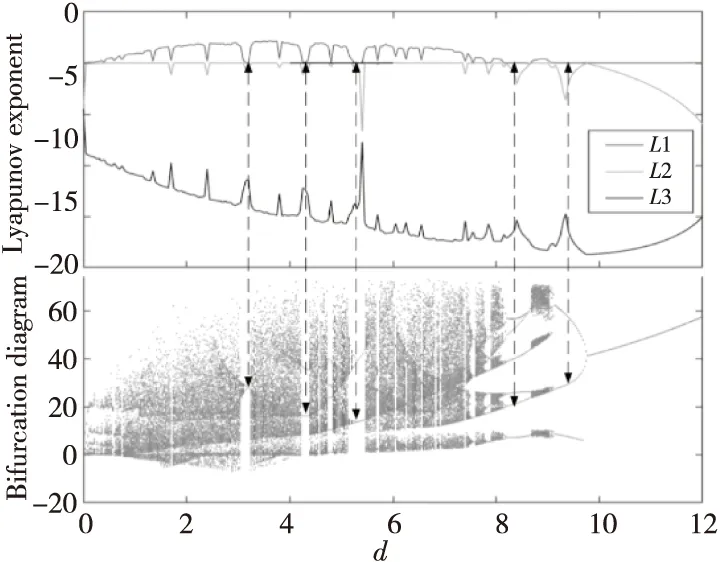
Figure 4 Lyapunov exponent and bifurcation diagram when parameter d changes within (0,12)圖4 參數(shù)d在(0，12)內(nèi)變化時的Lyapunov指數(shù)譜與分岔圖

Figure 5 Attractor phase diagram with different values of parameter d 圖5 參數(shù)d取不同值時的吸引子相圖

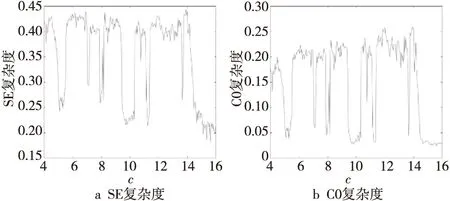
Figure 6 System complexity with the change of parameter c圖6 參數(shù)c變化時系統(tǒng)的復雜度

2.4 SE復雜度與C0復雜度分析

系統(tǒng)復雜性測度對混沌系統(tǒng)動力學分析具有重要意義，大量研究表明，混沌系統(tǒng)的復雜度越高，越適合用于保密通信[15,16]。SE復雜度反映了傅里葉變換域的無序狀態(tài)，譜越平坦，其SE復雜度越大，說明時間序列的復雜性越高。C0復雜度也是基于離散傅里葉變換，但它反映序列中不規(guī)則的比例[17,18]。計算系統(tǒng)的SE復雜度與C0復雜度與圖3中的Lyapunov指數(shù)譜和分岔圖中所使用的參數(shù)c相對應，如圖6所示，當系統(tǒng)處于周期振蕩時，對應的SE復雜度與C0復雜度較小，說明此時系統(tǒng)復雜度較低。當系統(tǒng)處于混沌狀態(tài)時，對應的SE復雜度與C0復雜度較大，此時系統(tǒng)復雜度較高。由此可見，系統(tǒng)復雜度與Lyapunov指數(shù)譜和分岔圖的變化趨勢相一致。

系統(tǒng)隨參數(shù)d變化的復雜度如圖7所示。從圖7可以看出，系統(tǒng)的SE復雜度與C0復雜度與圖4的Lyapunov指數(shù)譜和分岔圖的變化趨勢相一致，當d大于9時，系統(tǒng)處于周期振蕩，SE復雜度與C0復雜度較小，此時系統(tǒng)的復雜度較低。當選取的參數(shù)d使得系統(tǒng)處于混沌振蕩時，對應的SE復雜度與C0復雜度較大，此時系統(tǒng)復雜度較高，即系統(tǒng)的混亂性越高。因此，SE復雜度與C0復雜度圖可以提供一種直觀、有效的參數(shù)配置方法。

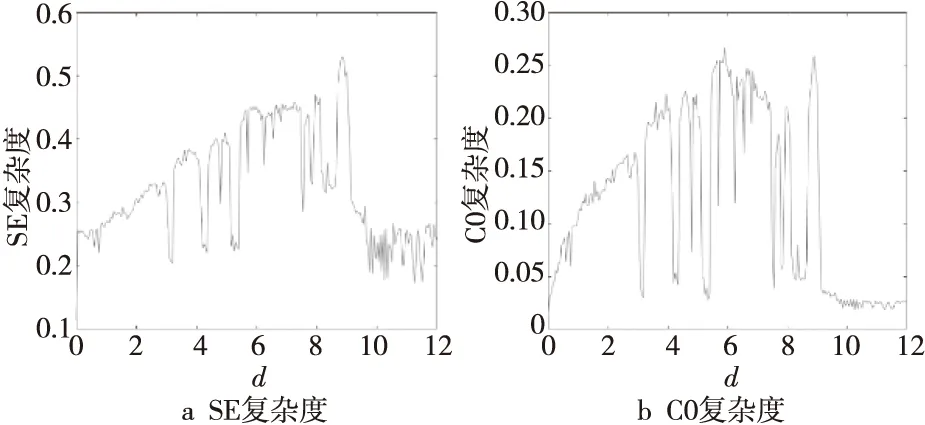
Figure 7 System complexity under the change of parameter d圖7 參數(shù)d變化時系統(tǒng)的復雜度

在實際應用中，SE復雜度和C0復雜度的混沌圖可以更好地為參數(shù)的選擇提供依據(jù)。圖8給出了參數(shù)c和d同時變化時SE復雜度與C0復雜度的混沌圖，在復雜度混沌圖中，顏色越深表示復雜度越高。在保密通信領(lǐng)域，復雜度越高表示隨機性越大，序列恢復的難度越大。因此，混沌系統(tǒng)在實際應用中，應盡可能地增加其復雜性，以保證擴頻系統(tǒng)具有良好的抗干擾性和較強的抗截獲性。在圖8中，選擇混沌程度較高的參數(shù)時，應考慮圖中間與左邊的參數(shù)，而沿右邊界的參數(shù)對任意的敏感程度較強，應盡量避免。

Figure 8 Chaos diagram of the system complexity with the changes of parameters c and d圖8 參數(shù)c、d同時變化時系統(tǒng)的復雜度混沌圖

3 系統(tǒng)電路設(shè)計與仿真

為了驗證該混沌系統(tǒng)的動態(tài)特性，本文利用Multisim軟件對其電路進行設(shè)計與仿真。電路采用3554AM運算放大器和AD633乘法器實現(xiàn)，供電電壓設(shè)為±15 V。為了便于該系統(tǒng)在實際電路中實施，對其進行時間尺度變換，令τ=100t得：

(7)

根據(jù)基爾霍夫電路定律，系統(tǒng)的電路狀態(tài)方程表示如式(8)所示：

(8)

將式(8)與式(7)進行比較,令C1=C2=C3=10 nF，可以得到其電阻參數(shù)，R1=R2=50 kΩ,R3=100 kΩ,R4=10 kΩ,R6=90.9 kΩ,R7=71.4 kΩ,R11=100 kΩ,R5=R8=R9=10 kΩ,R10=R12=200 kΩ，電路原理如圖9所示。根據(jù)所設(shè)計的電路和給定的元件參數(shù)進行Multisim仿真，在虛擬Tektronix示波器上可以觀察到相圖，如圖10所示，電路實驗結(jié)果與數(shù)值仿真結(jié)果相一致，證實系統(tǒng)是準確的。

4 混沌系統(tǒng)同步控制

混沌因其不可預測性和高度偽隨機性在保密通信領(lǐng)域得到了廣泛的應用[19,20]。利用混沌的時間復雜性和表面隨機性，可以將要傳輸?shù)男畔㈦[藏在混沌信號中，然后在接收端采用混沌同步技術(shù)獲取有用信息[21,22]。本文采用非線性反饋與線性反饋2種方法實現(xiàn)2個混沌系統(tǒng)的同步，并對線性反饋同步電路進行了仿真。響應系統(tǒng)具有與驅(qū)動系統(tǒng)相同的電路結(jié)構(gòu)，但其初始值不同。隨著時間的推移，2個相同的混沌系統(tǒng)可以在其狀態(tài)變量之間實現(xiàn)并保持同步。

Figure 9 Circuit schematic圖9 電路原理圖

Figure 10 Circuit simulation experiment results圖10 電路仿真實驗結(jié)果

4.1 非線性反饋同步控制

設(shè)系統(tǒng)(1)為驅(qū)動系統(tǒng)，加入控制項后的響應系統(tǒng)數(shù)學模型如式(9)所示：

(9)

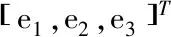
(10)

由此可將原同步問題轉(zhuǎn)化為誤差系統(tǒng)式(10)在原點(0，0，0)處的漸進穩(wěn)定性問題。

定理1對于驅(qū)動系統(tǒng)(1)與響應系統(tǒng)(9)，若取系統(tǒng)的非線性控制律如式(11)所示:

(11)

證明將控制律式(11)代入誤差系統(tǒng)式(10)得:

(12)

構(gòu)造如式(13)所示的Lyapunov函數(shù):

(13)

將式(13)分別沿著誤差向量e求導，并結(jié)合式(10)，得：

(14)

□

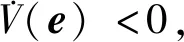
利用Matlab軟件進行數(shù)值仿真，設(shè)驅(qū)動系統(tǒng)(1)的初始值為：x(0)=1，y(0)=2，z(0)=3，響應系統(tǒng)(9)的初始值為:x1(0)=4，y1(0)=5，z1(0)=6，控制器參數(shù)取k=-13，則該混沌系統(tǒng)同步時驅(qū)動和響應系統(tǒng)的狀態(tài)變量隨時間的變化情況與系統(tǒng)誤差收斂曲線如圖11所示。

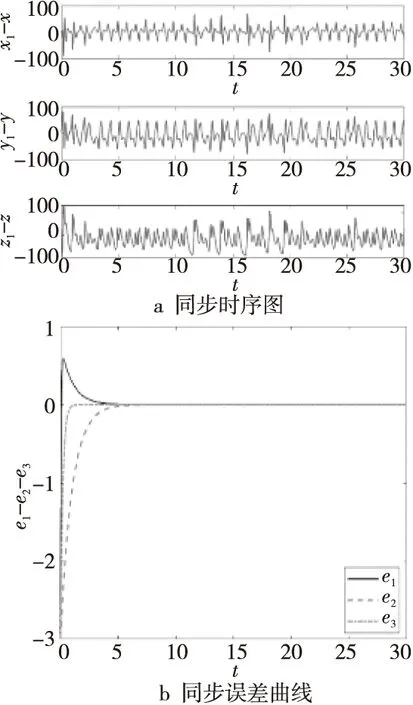
Figure 11 Timing diagram and error curve of system synchronization圖11 系統(tǒng)同步的時序圖與誤差曲線

仿真結(jié)果顯示，所設(shè)計的非線性反饋控制律可以使驅(qū)動系統(tǒng)(1)與響應系統(tǒng)(9)達到同步。但是，上述所設(shè)計的非線性反饋控制器比較復雜，在電路實現(xiàn)方面較為不易，如何進一步簡化控制律結(jié)構(gòu)與優(yōu)化系統(tǒng)同步方法就顯得極為重要。由于線性反饋控制同步電路簡單且在物理實現(xiàn)上較為容易，故下面采用線性反饋控制方法，通過系統(tǒng)的最大Lyapunov指數(shù)來確定控制參數(shù)的取值范圍，從而達到該系統(tǒng)的同步控制，并對其設(shè)計電路仿真實驗來驗證此方法的可行性。

4.2 線性反饋同步控制

基于線性反饋同步方法，當選取系統(tǒng)參數(shù)a=20，b=14，c=11，d=5時，在式(1)上加入控制項后將其設(shè)為響應系統(tǒng)，其數(shù)學模型如式(15)所示：

(15)

其中k為線性控制參數(shù)。令e1=x1-x，e2=y1-y，e3=z1-z，則誤差系統(tǒng)方程可由式(15)減去式(1)得到,如式(16)所示：

(16)

設(shè)驅(qū)動系統(tǒng)的初始值為：x(0)=1,y(0)=1,z(0)=1，響應系統(tǒng)的初始值為：x1(0)=10,y1(0)=10,z1(0)=10，取步長T=0.01，由數(shù)值計算可得，系統(tǒng)的最大Lyapunov指數(shù)LEmax=2.487≈2.5。根據(jù)線性反饋同步控制機理[23,24]，當取控制參數(shù)k>LEmax時，采用線性反饋控制方法，可以使混沌系統(tǒng)達到同步。控制參數(shù)k取不同值時的同步誤差曲線和時域波形如圖12所示。

Figure 12 Numerical simulation of system synchronization圖12 系統(tǒng)同步數(shù)值仿真

由數(shù)值仿真結(jié)果可得，當k=2時，驅(qū)動系統(tǒng)與響應系統(tǒng)不同步；當k=2.5時，驅(qū)動系統(tǒng)與響應系統(tǒng)經(jīng)過一段時間后最終達到同步；當k=3.5時，驅(qū)動系統(tǒng)與響應系統(tǒng)經(jīng)過短暫時間后達到同步。由上述可得，當k大于系統(tǒng)最大Lyapunov指數(shù)時，誤差曲線最終收斂于0，時域波形也達到同步，并且當k越大時，達到同步所需要的時間越短。相比文獻[6]中的耦合同步，根據(jù)最大Lyapunov指數(shù)能夠更精確地控制混沌系統(tǒng)同步。

為了驗證上述理論分析與數(shù)值仿真的正確性，在Multisim軟件上對其進行同步電路仿真實驗，由圖9可得，C4=C5=C6=10 nF,R14=90.9 kΩ,R15=71.4 kΩ,R19=50 kΩ,R20=50 kΩ,R21=100 kΩ,R22=200 kΩ,R23=100 kΩ,R24=200 kΩ。同步電路原理如圖13所示。相比文獻[23]中的同步控制電路，此控制電路減少了一組反相比例放大電路，使得電路更加簡單、易實現(xiàn)。

Figure 13 Simulated circuit diagram of synchronous circuit圖13 同步電路仿真電路圖

當R29=R39=R44=500 kΩ時，k=2；當R29=R39=R44=400 kΩ時，k=2.5；當R29=R39=R44=285 kΩ時，k=3.5。當k取不同值時，相應的狀態(tài)變量的相圖如圖14所示，同步時x1-x2的時域波形相重合，并且其相圖為一條通過原點的直線。而且隨著k值的增大，2個混沌系統(tǒng)達到同步時所用到的時間越少，由此可見電路實驗結(jié)果與數(shù)值仿真結(jié)果一致，證明了此方法的可行性。

Figure 14 Simulation results of chaotic synchronization circuit圖14 x1與x2同步仿真實驗相圖

5 結(jié)束語

本文根據(jù)Bao系統(tǒng)的構(gòu)建模式，提出一個新的三維混沌系統(tǒng)。對新系統(tǒng)的吸引子相圖、Poincare截面、0-1測試以及Lyapunov指數(shù)譜與分岔圖等基本動力學特性進行了研究分析，結(jié)果表明該系統(tǒng)具有新的拓撲結(jié)構(gòu)和更為復雜無序的混沌特性。此外，通過計算譜熵(SE)復雜度與C0復雜度，為電路參數(shù)的選取提供了一種直觀有效的方法。利用Multisim軟件設(shè)計實現(xiàn)了該系統(tǒng)電路，仿真結(jié)果證實了理論分析與數(shù)值仿真的正確性。最后，采用非線性反饋與線性反饋控制方法實現(xiàn)了該混沌系統(tǒng)的同步，給出了系統(tǒng)線性同步控制參數(shù)的范圍，使得同步控制更加精確與嚴謹，并通過數(shù)值仿真與電路實驗證實了此方法的有效性。但是，該方法在保密通信領(lǐng)域中的應用還有待進一步研究，并且其硬件電路還有待實現(xiàn)。