工業機器人PTP運動的研究與仿真

鄭博濤，郭永勝，潘冠東

(遼寧加寶石化設備有限公司，遼寧 營口 115004)

0 引言

壓力容器生產制造企業在采購材料后，需要按照批號、材質和標準等擺放，考慮人工勞動強度及擺放效率，應用機器人代替人工進行作業，將人們從繁重的生產任務中解放出來。為了使工業機器人能夠較為理想地完成人們預定的要求，則需要對工業機器人的運動進行研究。PTP運動(即點到點的運動)是工業機器人的主要運動方式之一，工件搬運工作都是通過點到點的運動來完成的，工業機器人的使用大大提高了工作效率，降低了企業的生產成本[1]。因此，本文通過對工業機器人的建模來對工業機器人PTP運動進行仿真分析，進而確保機器人在工作過程中的使用性能[2]。

1 機器人參數及連桿坐標系的建立

本文以FANUC R-2000iB型工業機器人為研究對象(見圖1)，其所有關節均為轉動關節，前三個關節控制機器人末端在空間中的位置，后三個關節控制機器人末端的方向。為了研究機器人末端位姿在基礎坐標系中的表示，在每個連桿上固接了一個坐標系，由D-H法則確定相鄰連桿之間的位姿，通過坐標變換即可得出機器人末端在基礎坐標系中的位姿，建立好的機器人連桿坐標系如圖2所示。

2 運動學分析

運動學是規劃操作臂軌跡的基礎，主要研究機器人關節變量與機器人末端在空間中的位姿對應關系，通過確定機器人連桿參數就可建立其運動學方程。確定連桿參數的方法如下：

(1) 關節轉角θi是由xi-1坐標軸到xi坐標軸繞著zi坐標軸所測得的角度。

(2) 連桿扭角αi-1是由zi-1坐標軸到zi坐標軸繞著xi-1坐標軸測得的角度。

(3) 連桿長度ai-1是zi-1坐標軸到zi坐標軸沿xi-1坐標軸所測得的距離。

(4) 連桿偏距di是xi-1坐標軸到xi坐標軸沿zi坐標軸所測得的距離。

圖1 FANUC R-2000iB工業機器人

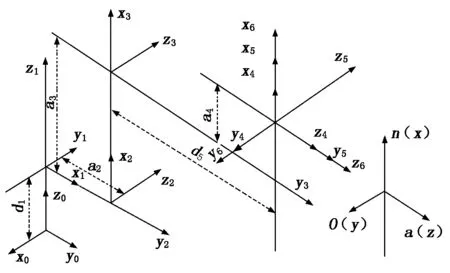
圖2 機器人連桿坐標系

由上述定義及圖2建立的坐標系可得R-2000iB型工業機器人的連桿參數，如表1所示。

由D-H法則可得相鄰兩個連桿的位姿關系，通過齊次矩陣變換得到機器人末端在基礎坐標系中的方位描述06T，具體如下：

06T==nxoxaxpxnyoyaypynzozazpz0001.

其中：分量nx、ox、ax為機器人末端相對于坐標系{O}的x軸的角度向量；分量ny、oy、ay為機器人末端相對于坐標系{O}的y軸的角度向量; 分量nz、oz、az為機器人末端相對于坐標系{O}的z軸的角度向量;px、py、pz為機器人末端相對于坐標系{O}的位置坐標。

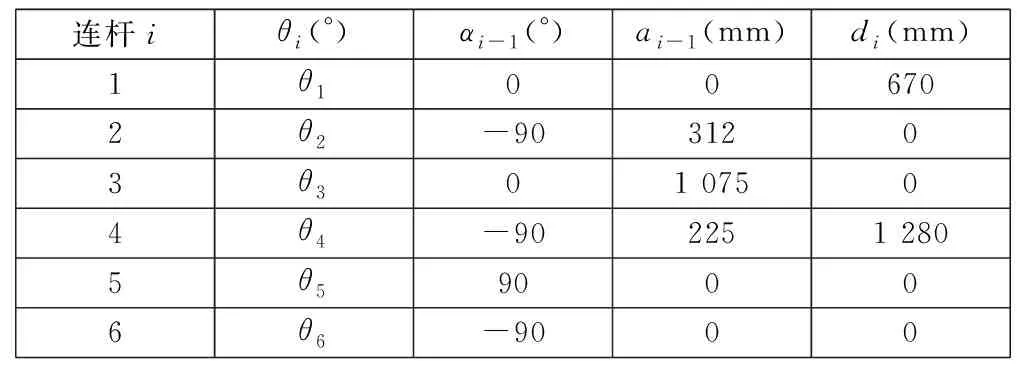
表1 機器人連桿參數

3 運動學仿真

本文使用MATLAB軟件中的機器人工具箱進行運動學仿真，通過調用內部的函數而不需要復雜的編程即可實現運動學仿真，很大程度上簡化了編程人員的工作任務，提高了對機器人運動學的研究效率[3-5]。

通過調用Link函數、Robot函數與drivebot函數即可建立工業機器人的三維模型(見圖3)，調用格式為L=LINK([alpha A theta D sigma],‘standard’)。其中，前4個參數分別表示連桿扭角、桿長、關節轉角、偏距；sigma代表關節是旋轉還是移動關節，0是旋轉關節，1是移動關節；standard表示使用標準的D-H參數進行建模。Robot函數將所有的連桿結合成一個整體，調用drivebot函數可以彈出關節滑塊控制器(見圖4)。具體的建模如下：

L1=link([0 0 0 670 0],’standard’);

L2=link([-pi/2 312 pi/2 0 0],’standard’);

L3=link([0 1075 pi 0 0],’standard’);

L4=link([-pi/2 225 pi 1280 0],’standard’);

L5=link([pi/2 0 pi 0 0],’standard’);

L6=link([-pi/2 0 0 0 0],’standard’);

r=robot({L1 L2 L3 L4 L5 L6});

r.name=’R-2000iB’;

drivebot(r);

圖3 機器人三維模型 圖4 機器人關節滑塊控制器

這里隨機選取了兩組關節變量，以機器人末端在空間中的位置為研究對象，通過對比計算得到的位置與仿真得到的位置來確定06T建立的正確與否。兩組變量值分別為q1=[0.188 5 0.439 82 -0.125 66 0.251 33 0.314 16 -0.251 33]，q2=[0.439 82 0.376 99 0.188 5 0.062 832 0.251 33 -0.314 16]。所得數據如表2所示。

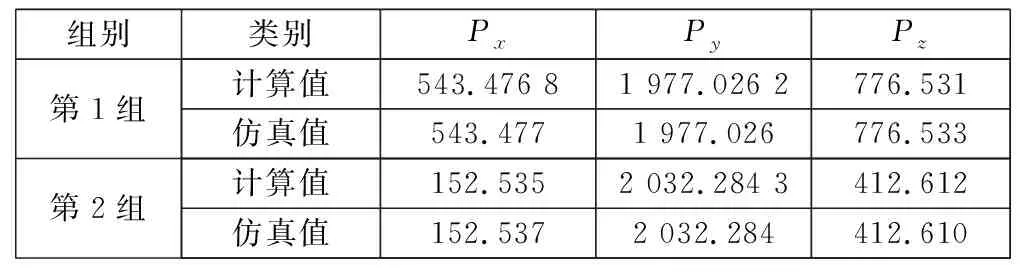
表2 機器人末端位置計算值與仿真值比較

分析比較上述數據，可以發現通過計算得到的位置數據與仿真得到的位置數據誤差較小，這說明上述建立的機器人末端在基礎坐標系下的位姿矩陣06T是可靠的。

4 PTP運動仿真

PTP運動只考慮初始點與終止點的位置，不需考慮機器人末端在三維空間中走過的具體運動軌跡，這樣只需在關節空間進行軌跡規劃即可，大大減少了計算量并避免了工業機器人發生奇異的情況。所謂軌跡規劃就是規劃關節角位移、關節角速度、關節角加速度隨時間變化的情況。同時，軌跡仿真也可以幫助人們更直觀地理解PTP運動的過程[6-8]。設定初始關節變量q1=[0 0 0 0 0 0]，q2=[pi/4 pi/3 pi/5 pi/4 pi/2 pi]，運動時間設定為2 s，通過如下的仿真程序，可以較為清晰地觀看到機器人從變量q1運動到q2的過程。

L1=link([0 0 0 670 0],’standard’);

L2=link([-pi/2 312 pi/2 0 0],’standard’);

L3=link([0 1075 pi 0 0],’standard’);

L4=link([-pi/2 225 pi 1280 0],’standard’);

L5=link([pi/2 0 pi 0 0],’standard’);

L6=link([-pi/2 0 0 0 0],’standard’);

r=robot({L1 L2 L3 L4 L5 L6});

r.name=’R-2000iB’;

qz=[0 0 0 0 0 0];

qr=[pi/4 pi/3 pi/5 pi/4 pi/2 pi];

t=0:0.1:2;

q=jtraj(qz,qr,t);

[q,qd,qdd]=jtraj(qz,qr,t);

subplot(3,3,1);plot(t,q(:,1));grid;xlabel(’t/s’); ylabel(’rad’); title(’關節1位移變化曲線’)；

subplot(3,3,2);plot(t,q(:,2));grid;xlabel(’t/s’); ylabel(’rad’); title(’關節2位移變化曲線’)；

subplot(3,3,3);plot(t,q(:,3));grid;xlabel(’t/s’); ylabel(’rad’); title(’關節3位移變化曲線’)；

subplot(3,3,4);plot(t,qd(:,1));grid;xlabel(’t/s’); ylabel(’rad/s’); title(’關節1角速度變化曲線’)；

subplot(3,3,5);plot(t,qd(:,2));grid;xlabel(’t/s’); ylabel(’rad/s’); title(’關節2角速度變化曲線’)；

subplot(3,3,6);plot(t,qd(:,3));grid;xlabel(’t/s’); ylabel(’rad/s’); title(’關節3角速度變化曲線’)；

subplot(3,3,7);plot(t,qdd(:,1));grid;xlabel(’t/s’); ylabel(’rad/s^2’); title(’關節1角加速度變化曲線’)；

subplot(3,3,8);plot(t,qdd(:,2));grid;xlabel(’t/s’); ylabel(’rad/s^2’); title(’關節2角加速度變化曲線’)；

subplot(3,3,9);plot(t,qdd(:,3));grid;xlabel(’t/s’); ylabel(’rad/s^2’); title(’關節3角加速度變化曲線’)；

通過調用函數plot(t,q(:,i))可得到關節變化的位移曲線，調用函數plot(t,qd(:,i))、plot(t,qdd(:,i))可分別得到關節角速度與關節角加速度曲線，如圖5所示。由于前3個關節控制機器人末端在空間中的位置，故本文取關節i=1,2,3進行仿真研究。

圖5中，3個旋轉關節的關節轉角都是從初始位置平緩地運動到終止位置，關節角速度都從零平緩地增大到最大值，再逐漸地減小到零，角加速度先正后負說明關節速度先增加后減小，可以發現以PTP運動方式運動的工業機器人在運動過程中的關節位移、角速度、角加速度都沒有發生突變的情況，其隨時間變化的曲線都較為平滑，說明工業機器人在運動過程中不會出現較大振動，可以很好地代替工人完成作業任務[9]。

圖5 機器人關節角位移、角速度、角加速度變化

5 結論

本文以FANUC R-2000iB工業機器人為研究對象，通過D-H法則建立機器人連桿坐標系與運動學方程，并使用MATLAB軟件中的機器人工具箱對D-H法則建立的運動學方程進行了仿真驗證，確定了運動學方程的正確性，并對工業機器人PTP運動做了仿真分析，確定了PTP運動的工業機器人的運動較為平緩，可以使用工業機器人完成人們預定的搬運作業任務。