混凝土簡支斜交箱型梁橋受力特性分析

李楊杰， 程京偉， 焦馳宇

(1.北京建筑大學未來城市設計高精尖創新中心， 北京 100044； 2.北京建筑大學工程結構與新材料北京高等學校工程研究中心， 北京 100044； 3.北京市市政工程設計研究總院有限公司， 北京 100082； 4.北京建筑大學北京節能減排關鍵技術協同創新中心， 北京 100044)

斜交橋不僅能適應已有交通環境，而且可以保證線路的線形流暢及行車舒適，在高等級公路中所占比例已達到40%～50%[1]，已成為很重要的橋型結構。

《公路鋼筋混凝土及預應力混凝土橋涵設計規范》(JTG 3362—2018)對斜板橋與直板橋的空間受力特性進行了對比分析，并對斜板橋給出了細節構造說明，但由于目前對斜梁橋與直梁橋的空間受力特性、位移特征缺乏對比研究，因而對其計算方法和構造工藝并未提出特殊規定。

學者們對斜板橋靜力特性開了廣泛的研究[2- 4]。在斜交框架橋方面，趙海濤等[5]利用ANSYS有限元軟件建模，分析了斜交框架橋在養護期的應力場分布特點與規律，認為斜交角度減小，頂板銳角一側最大拉應力減小，鈍角一側拉應力增大，斜交角度對中心線位置處應力變化沒有影響。竇國濤等[6]對不同土壓力工況下正交框架橋與斜交框架橋的受力性能進行了研究，認為斜交框架橋位移和應力極值絕對值稍大于正交框架橋。在斜梁橋方面，黃平明等[7]分析了支承剛度對斜梁橋內力產生的響應，結果表明：調整端橫梁抗彎剛度和支座厚度可有效地調整斜梁內力。金秀輝等[8]對預應力混凝土矮肋T斜梁橋進行了實驗研究，表明在偏載作用下，預應力混凝土矮肋T斜梁橋會產生向上的支座反力，但不會產生銳角或鈍角上翹現象。孫勝江[9]研究表明，連續斜梁橋在支座處存在很大的扭矩，斜度越大，扭矩越大。戴公連等[10]對15°斜交角下連續鋼箱梁橋橫隔板布置方式進行了研究，結果表明：當斜交角度小于15°時，橫隔板正交與斜交的布置方式對結構受力影響不大。劉聰[11]對T型簡支斜梁橋的彎扭耦合效應進行研究，結果表明：簡支斜梁在豎向力作用由于彎扭耦合力的作用，跨中彎矩隨著斜交角的增大而減小。Wu等[12]利用振動臺試驗，研究了單跨簡支單箱五室梁橋在斜交角度超出自由轉動極限范圍時的脫座問題，認為當斜交角度超出極限范圍時，單跨橋梁的最小支撐長度應根據抗震要求而不是幾何要求進行設計。Mohseni等[13]對單箱三室連續斜梁橋的扭矩研究表明，扭轉剛度和活載位置對橋梁的內力響應影響很大。綜上可知，中外學者圍繞簡支或連續斜梁橋開展了大量研究，但多集中于板梁、T梁橋、單箱多室梁橋，而針對中國簡支小箱型梁橋這一公路橋梁的常用形式還缺乏系統性的研究。

為此，結合工程實例，對斜梁橋與直梁橋進行受力特性對比，探討斜梁橋在支反力，支點位移和主梁內力與直梁橋的不同。以此分析在構造細節中需考慮的關鍵問題，以便于指導工程設計。

1 工程概況

以一座36 m斜交簡支小箱梁橋為工程背景開展研究。橋梁斜交角度為30°，設計荷載等級為城-A級，橋面寬為40 m(機動車橋面寬23.06 m)，為了保證機動車道和非機動車道的行車線形，在橋區范圍內橋梁斷面按機、非橋梁分離進行設計。立面圖如圖1所示，平面圖如圖2所示，主梁跨中橫斷面如圖3所示。

D為樁的直徑；L為樁身長度圖1 橋梁立面圖Fig.1 Elevation viewof bridge

圖2 橋梁平面圖Fig.2 Plan view of bridge

圖3 橋梁1/2跨中橫斷面圖Fig.3 1/2 span mid cross section of bridge

2 模型建立

研究表明，對于寬跨比較大且為箱梁式上部結構的斜橋而言，采用傳統的單梁分析方法雖然建模簡單，但很難模擬斜橋的空間受力特點；采用板單元或實體單元的分析方法雖然模型仿真精確度高，但計算量較大，耗費時間過多，且提取的結果不直觀，不便于在工程實際中廣泛采用。研究表明，對于寬跨比大于0.5，斜交角大于15°的斜交橋梁在實際工程中宜采用梁格法分析[14]。由于在橋區范圍內橋梁斷面按機、非分離進行設計，只針對機動車部分的小箱梁橋整體進行研究。機動車主橋部分寬跨比為0.64，斜交角為30°因此整體橋跨結構采用斜交網格進行劃分，縱梁為8片小箱梁，橫梁設虛擬橫梁和橫隔板，均采用空間梁單元模擬。其中在梁端以及跨中處設置橫隔板，跨中的橫隔板與虛擬橫梁用T梁模擬，模型中虛擬橫梁的布置采用等分原則，劃分的間距設為1 m，在端橫梁處進行加密，劃分間距為0.5 m。支座采用板式橡膠支座，其3個方向的平動彈性剛度系數分別為Sdx=740 890 kN/m，Sdy=Sdz=2 057 kN/m；3個方向的轉動彈性剛度系數分別為Srx=62 kN·m/rad，Sry=Srz=11 118 kN·m/rad。斜橋的受力特性分析主要研究上部結構，對于下部結構采用固定約束簡化處理。模型共計737個單元，448個節點。有限元模型如圖4所示。

圖4 斜橋有限元模型Fig.4 Finite element model of skew bridge

直橋空間梁格法模擬橋跨結構，采用正交網格進行劃分，其他構造模擬與斜橋相同。直橋有限元模型如圖5所示。

圖5 直橋有限元模型Fig.5 Finite element model of straight bridge

3 結構計算分析

為分析混凝土簡支斜梁橋受力特性。直橋與斜橋模型中考慮以下6種具有代表性的荷載工況進行研究分析，如表1所示。

表1 荷載工況Table 1 Load cases

3.1 反力對比分析

為了對結構支座及主梁局部承壓進行良好設計，在此比較了斜交橋梁的支座反力。在反力分析中，支座編號1～16如圖6所示。將直橋與斜橋的6種組合工況包絡支反力結果按照編號進行對比，如圖7所示。從圖7可知，在組合工況作用下，采用梁格法建立模型時，無論是直梁橋還是斜梁橋，邊支座與中支座反力均有一定差異。而斜交橋除此特征外，支反力不均勻度更大，且銳角處的支反力小于直橋，鈍角處的支反力遠大于直橋。就斜橋自身支反力而言，鈍角與銳角支反力差異大，鈍角附近處的支反力變化大。

圖6 支座編號Fig.6 Support number

圖7 支座反力對比Fig.7 Comparison of support and reaction forces

3.2 位移對比分析

支反力研究表明，在組合工況作用下，斜橋豎向內力以恒載作用為主，其內力服從就近傳遞原則。在此基礎上分析整體三維位移結果。研究表明，通過考慮在組合包絡工況作用下，3個方向位移中豎向位移相差不大，水平位移相差較大。在此展示出結構位移以恒載及收縮徐變作用下平面變形形態進行深入分析。斜梁橋平面位移如圖8(a)所示，直橋平面位移如圖8(b)所示。

由位移圖(圖8)可知，斜橋整體平面橫向位移大于直橋，且出現平面扭轉現象，表現在支承邊處鈍角向銳角方向扭轉6°。結果表明，斜交角的存在以及支座水平剛度對主梁有一定的非對稱約束作用，導致收縮徐變下結構產生了非對稱變形。

圖8 橫向位移Fig.8 Transverse displacement

3.3 內力對比分析

為了更加清楚的了解直橋與斜橋的受力特點，在此對直橋與斜橋的內力進行對比分析。如圖9所示，提取直橋與斜橋的縱向彎矩My、扭矩Mx結果并進行對比分析。

在組合包絡工況作用下，將直橋與斜橋的邊梁和中梁的縱向彎矩進行比較如圖10所示。可以看出，直橋與斜橋在組合包絡工況作用下，斜橋跨中最大彎矩略微大于直橋跨中最大彎矩，且直橋和斜橋的邊梁與中梁縱向彎矩數值相差較小。

對比分析在組合包絡工況作用下，直梁橋與斜橋的邊跨與中跨的扭矩如圖11所示。

Mz為橫向彎矩圖9 內力示意圖Fig.9 Schematic diagram of internal forces

圖10 縱向彎矩對比Fig.10 Comparison of longitudinal bending moments

圖11 扭矩對比Fig.11 Torque comparison of middle beam

由圖11可知，在組合包絡工況作用下，直橋與斜橋均存在扭矩，但斜橋的扭矩大于直橋的扭矩。斜橋邊梁最大扭矩是直橋邊梁最大扭矩的2.06倍，斜橋中梁最大扭矩是直橋中梁最大扭矩的1.66倍。

直橋的扭矩是由于車輛荷載的橫向加載方式給箱梁造成了偏心加載所導致的。相比于直橋，由于斜度的存在，自重與二期荷載和預應力荷載都產生了支反力的不均勻分布，因而對斜橋箱梁造成偏心受壓和扭轉，疊加上車輛荷載后進一步加大了扭矩。

3.4 設計措施

通過上述綜合對比分析，建議對斜梁橋采取以下設計措施。

(1)在結構支座選型時采用不同噸位的支座，或者以鈍角處和銳角處受力為依據選取支座。考慮到鈍角支反力過大，建議對主梁考慮局部承壓措施。由于本例計算分析中未出現負反力，所以選取直徑550 mm，豎向承載能力為2 600 kN的圓形板式橡膠支座，且圓形支座因不分方向，比較適合斜橋；由于小箱梁在支點處采用實體箱型截面，且構造鋼筋密布，經驗算滿足局部承壓要求，因而對本橋不專門設置局部承壓措施。

(2)在結構的鈍角或銳角位置處設置防落梁裝置阻止主梁在收縮徐變及車輛荷載作用下的旋轉和爬移。在本例中，綜合考慮收縮徐變、車輛荷載及地震作用而出現的平面旋轉特性，特在距箱梁支座50 cm處設置橫向擋塊，在濕接縫與蓋梁交接處設置豎向限位設施，如圖12所示。

圖12 防落梁裝置Fig.12 Anti-drop-beam device

(3)考慮到扭矩的影響，通過增強截面尺寸、加密抗扭箍筋，提高截面抗扭能力。結合本例，由于車道寬度、建筑高度受限，無法調整梁高、梁寬。在實際工程中將跨中截面腹板厚度由200 mm增加到220 mm，同時抗扭箍筋間距由200 mm加密到120 mm。根據《公路鋼筋混凝土及預應力混凝土橋涵設計規范》(JTG 3362—2018)得到在組合包絡工況作用下，開裂扭矩Tcr由-704.25 kN·m增長到-723.04 kN·m，增長率為2.66%，極限扭矩Tu邊梁與中梁對比如圖13、圖14所示。

由圖13、圖14可知，在組合工況作用下，跨中采用200 mm腹板的截面，在中梁靠近鈍角處的跨中段作用效應Td=-1 175.19 kN·m，邊梁Td=-1 275.61 kN·m超過了構件承載力極限Tu=-1 131.32 kN·m，結構抗扭失效。增加腹板厚度20 mm，加密抗扭箍筋間距到120 mm邊梁與中梁的跨中抗扭失效段極限扭矩Tu由-1 131.32 kN·m增長到-1 611.04 kN·m，增長率為42.40%，并大于Td，結構穩定。通過以上對比發現，通過增加腹板厚度和加密抗扭箍筋對結構的開裂扭矩Tcr提升較小，但對極限扭矩Tu有較大提升。

根據閉合薄壁箱理論，箱形截面側壁產生剪應力流，只增加腹板厚度對開裂扭矩能力提升較小。由于鋼筋混凝土構件的極限扭矩由受扭箍筋與混凝土截面共同承擔，所以通過縮小受扭箍筋之間的間距來提高箍筋的受扭承載能力，從而提升構件的抗扭能力。

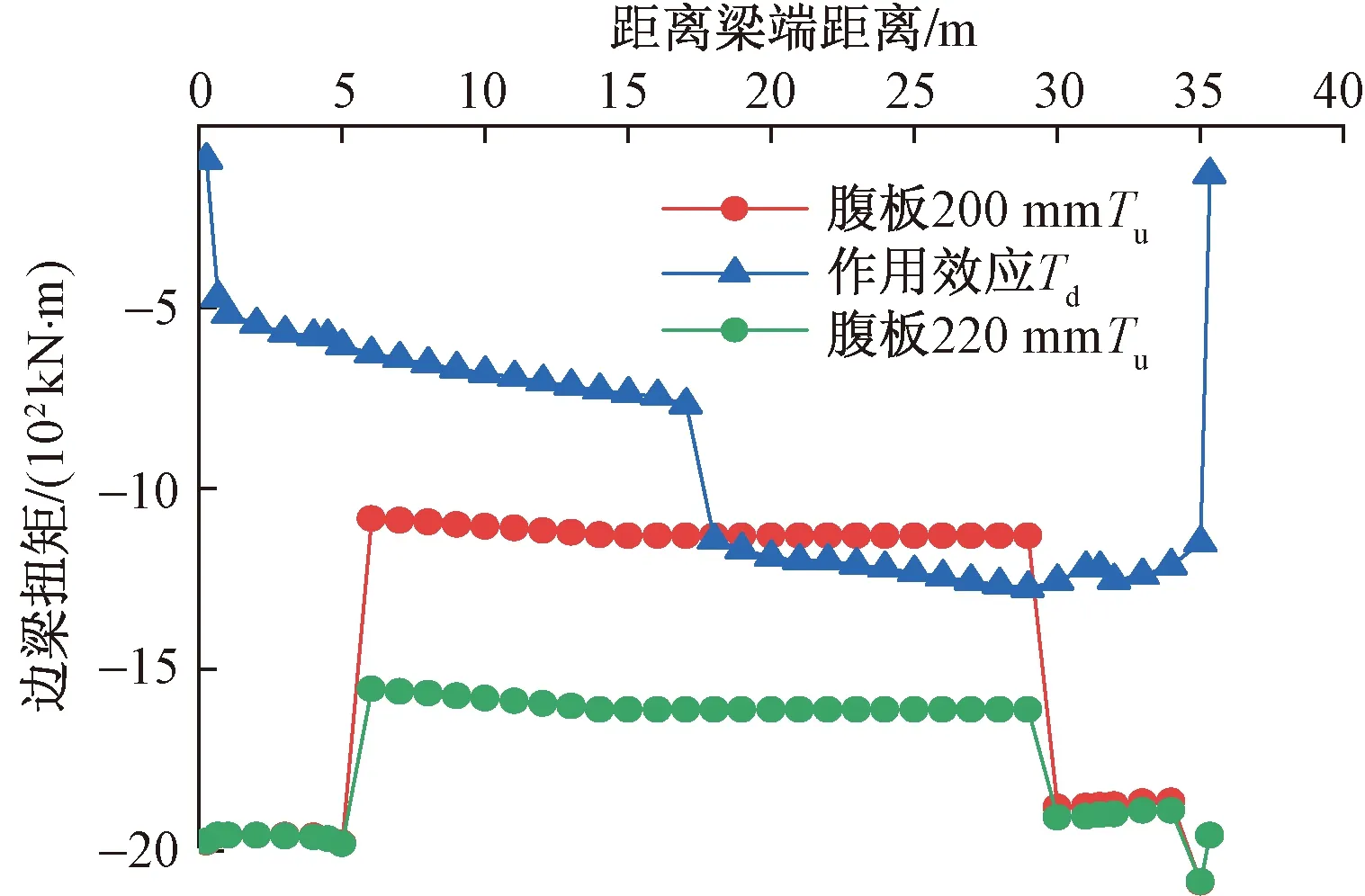
圖13 腹板改變的邊梁扭矩對比Fig.13 Comparison of side beam torque for web change

圖14 腹板改變的中梁腹板扭矩對比Fig.14 Comparison of middle beam torque for web change

4 結論

(1)斜交橋相較于直橋，支反力不均勻度更大，且銳角處的支反力小于直橋，鈍角處的支反力遠大于直橋。在設計措施中，可按照鈍角處最大支反力進行支座設計，并注意加強鈍角處的支座抗壓強度，避免局部應力過大，造成鈍角處主梁局部損傷。

(2)由于斜交角的存在以及支座水平剛度對主梁有一定的非對稱約束作用，導致收縮徐變下斜交橋產生了非對稱變形，表現為斜交橋整體平面橫向位移大于直橋，且出現平面扭轉現象。為防止上述現象造成落梁危害，在設計中應注意設置橫向擋塊和豎向限位設施。

(3)斜橋與直橋相比，由于斜度的存在，恒載產生了支反力的不均勻分布，因而對斜橋箱梁造成偏心受壓和扭轉，疊加車輛荷載后進一步加大了扭矩，從而導致斜橋的扭矩比直橋扭矩大。在實際工程設計中，當車道寬度、建筑高度受限無法調整梁高、梁寬時，可以通過增加截面腹板厚度和加密受扭箍筋來有效提高結構的抗扭承載能力。