采用壓-拉桿模型計算型鋼混凝土深梁承載力
盧化松
(基準(zhǔn)方中建筑設(shè)計股份有限公司,成都 610011)
1 引言
深梁是指跨度與其高度之比較小的梁。我國GB 50010—2010《混凝土結(jié)構(gòu)設(shè)計規(guī)范》[1](2015年版)(以下簡稱《結(jié)構(gòu)規(guī)范》)規(guī)定,跨高比l0/h<2的簡支梁或l0/h<2.5的連續(xù)梁屬于深梁。型鋼混凝土(SRC)深梁由于其承載力高等優(yōu)點,已廣泛應(yīng)用于高架車站、住宅轉(zhuǎn)換中。
SRC深梁因其跨高比較小,受外力作用時,內(nèi)部受力較復(fù)雜:存在受壓、受彎及受剪狀態(tài),平截面假定不再適用,經(jīng)典的梁理論設(shè)計方法已不適宜,而壓-拉桿模型提供了解決方案。
壓-拉桿模型起源于桁架模型,它將鋼筋混凝土構(gòu)件簡化為混凝土壓桿、鋼筋拉桿以及節(jié)點區(qū)。壓-拉桿模型能有效反映構(gòu)件的傳力機制,設(shè)計過程簡單。在國內(nèi),葉列平[2]、貢金鑫[3]等對壓-拉桿模型的應(yīng)用進行了研究,取得了較好的效果。
根據(jù)圣維南原理,壓-拉桿模型將構(gòu)件分為B區(qū)和D區(qū),B區(qū)為應(yīng)力線性分布,滿足平截面假定;D區(qū)較高的剪應(yīng)力使截面發(fā)生明顯翹曲,平截面假定不再適用。在梁的正截面受彎及斜截面受剪設(shè)計時,對于B區(qū),我國規(guī)范采用極限狀態(tài)法進行承載力的計算,理論較為成熟;對于D區(qū),通常采用經(jīng)驗計算或局部加強構(gòu)造措施,缺乏理論指導(dǎo)。壓-拉桿模型可真實反映D區(qū)的荷載傳遞機制,是D區(qū)截面設(shè)計的一種簡便的方法。
本文采用荷載路徑法,確定SRC深梁的壓桿、拉桿及節(jié)點區(qū)強度,合理考慮型鋼在壓-拉桿中的強度,建立節(jié)點平衡方程。通過分析SRC深梁的破壞模式,得出SRC深梁的實際承載力。
2 SRC深梁壓-拉桿模型
在豎向荷載作用下,SRC深梁受力模式分析可簡化為壓-拉桿模型,即將受拉開裂的混凝土和型鋼受壓部分等效為壓桿,將受拉縱筋和型鋼受拉翼緣等效為拉桿,將壓-拉桿的交匯區(qū)域看成節(jié)點。根據(jù)荷載分布情況,由結(jié)構(gòu)力學(xué)方法可以求出拉桿、壓桿、節(jié)點的內(nèi)力,并應(yīng)滿足式(1)要求:

式中,N為拉桿、壓桿和節(jié)點的軸力;Nu為拉桿、壓桿和節(jié)點的軸向承載力。
壓-拉桿模型較合理地反映了混凝土深梁的受力狀況,滿足塑性下限定理。因此,結(jié)構(gòu)實際承載力大于按壓-拉桿模型所預(yù)測的承載能力,簡化模型是安全可行的。建立壓-拉桿模型應(yīng)依據(jù)結(jié)構(gòu)的應(yīng)力分布圖,目前主要有:應(yīng)力跡線法、有限元法等[4]。本文對拉桿、壓桿、節(jié)點區(qū)進行分析。
2.1 拉桿
拉桿由縱向受拉鋼筋和型鋼受拉翼緣及其周圍同軸線的混凝土組成。拉桿承載力Ntu按式(2)計算:

式中,fy、fa分別為鋼筋、型鋼的屈服強度;Ast、Aa分別為受拉鋼筋、型鋼受拉翼緣的面積。
2.2 壓桿
壓桿代表模型中壓力場的合力,根據(jù)壓力擴散情況,可以分為棱柱形、瓶形和扇形,如圖1所示。一些學(xué)者建議水平壓桿使用棱柱形、斜壓桿使用瓶形,如圖2所示,圖2中P為梁承擔(dān)的集中荷載。本文采用上述學(xué)者的建議,根據(jù)《結(jié)構(gòu)規(guī)范》并參考ACI規(guī)范[5],建立鋼筋混凝土受壓桿件的計算公式。
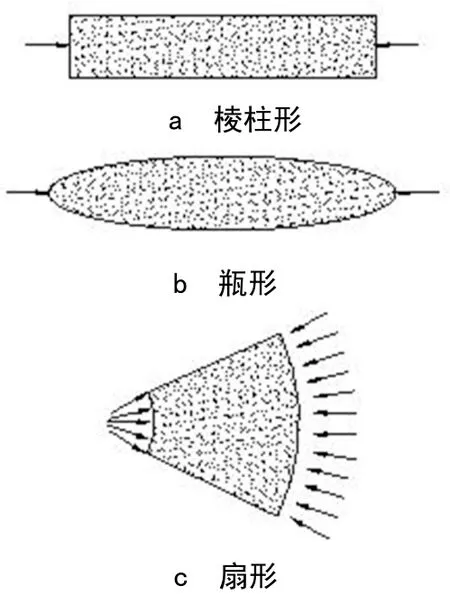
圖1 壓桿的類型
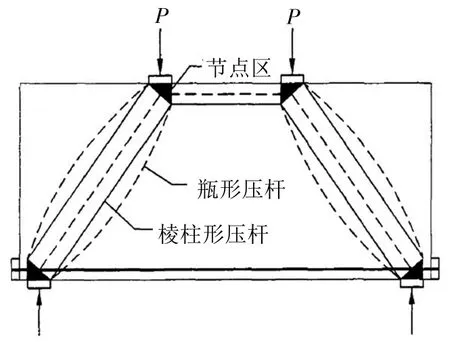
圖2 壓-拉桿模型
水平壓桿承載力Ncu按式(3)計算:
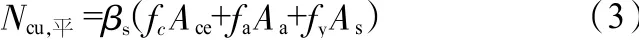
斜壓桿承載力Ncu按式(4)計算:
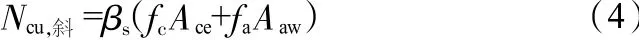
式中,fc為壓桿混凝土抗壓強度;Ace、Aa、Aaw、As分別為壓桿端的混凝土截面面積、型鋼受壓翼緣面積、斜壓桿型鋼受壓腹板面積、受壓鋼筋面積;βs為壓桿有效抗壓強度影響系數(shù),按表1取值。
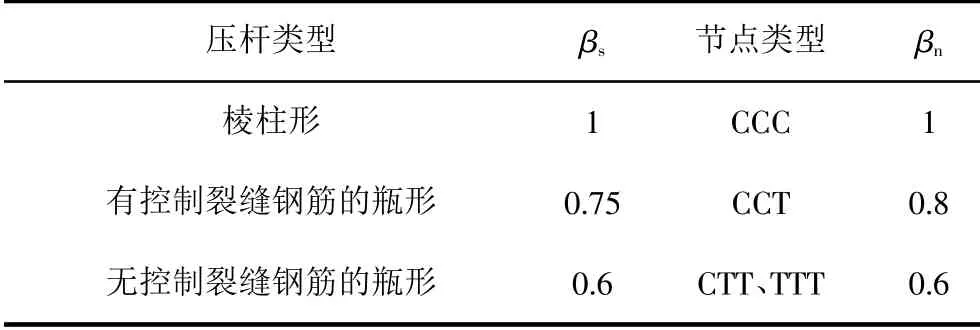
表1 βs、βn的取值
由于深梁中的假想壓桿受周圍介質(zhì)的約束,一般不會失穩(wěn),故式(3)和式(4)未考慮穩(wěn)定系數(shù)。另外,《結(jié)構(gòu)規(guī)范》公式為了統(tǒng)一可靠度,對式(3)和式(4)的右端項乘以系數(shù)0.9,這在壓-拉桿模型中可不考慮。
為控制裂縫,壓桿橫截面配筋應(yīng)滿足式(5):
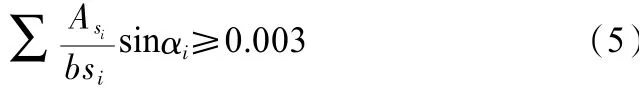
式中,αi為壓桿軸線與鋼筋軸線的夾角;Asi為與壓桿方向成α角度的鋼筋層中,間距si鋼筋的總面積,見圖3;b為深梁截面寬度。
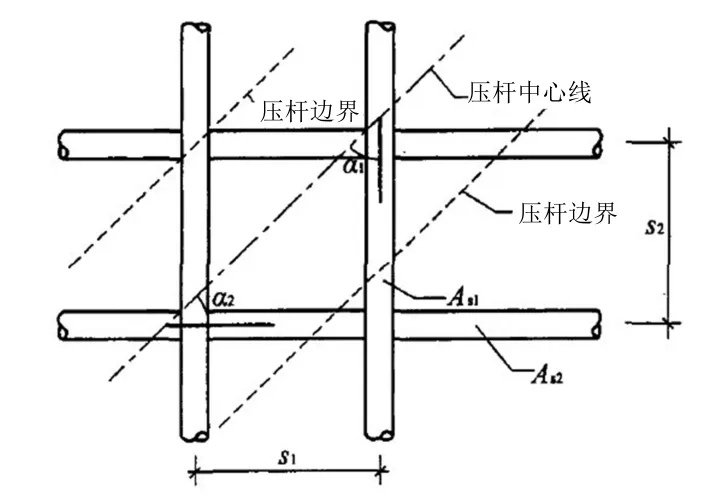
圖3 與壓桿相交的鋼筋
2.3 節(jié)點區(qū)
為了滿足壓-拉桿模型的受力平衡,節(jié)點區(qū)的受力狀態(tài)可簡化為3個集中作用力。根據(jù)受力狀態(tài)的不同,節(jié)點區(qū)可分為3個壓力節(jié)點(CCC)、兩個壓力和一個拉力節(jié)點(CCT)、一個壓力和兩個拉力節(jié)點(CTT)、3個拉力節(jié)點(TTT),如圖4所示。對于不同的節(jié)點類型,節(jié)點區(qū)的容許壓力Nnu按式(6)計算:
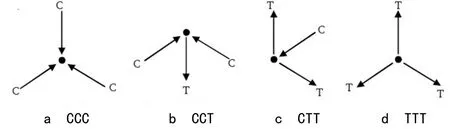
圖4 節(jié)點類型

式中,Aaw為節(jié)點區(qū)的斜壓桿型鋼腹板有效受壓面積,對水平桿件可取為0;βn為不同類型節(jié)點對應(yīng)的強度折減系數(shù),其取值如表1所示[2]。
2.4 SRC深梁壓-拉桿模型的建立
對于任意一個SRC簡支深梁,在對稱荷載作用下,簡化的壓-拉桿模型如圖5所示,虛線表示壓桿、實線表示拉桿。壓-拉桿組成的模型是機構(gòu)的,在A、D之間布置桿件,構(gòu)成穩(wěn)定體系。
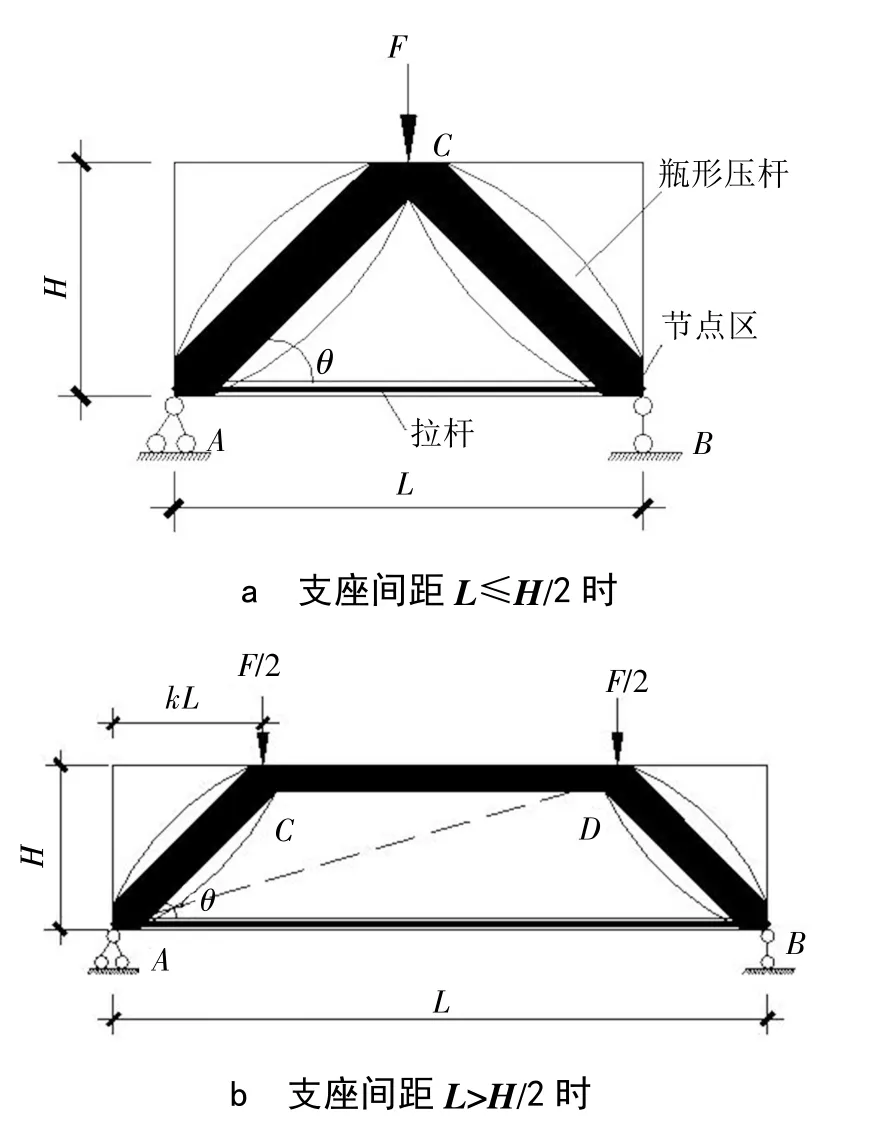
圖5 對稱荷載下的拉壓桿模型
對深梁梁端支座處的墊板,參考《結(jié)構(gòu)規(guī)范》中局部受壓承載力計算公式,其長度xR可近似按式(7)確定:

式中,F(xiàn)/2為支座集中反力;βc為混凝土強度影響系數(shù),C50及以下取1.0,C80及以上取0.75,中間強度按插值法計算;βl為局部受壓面積比,支座處取1.0。
AB拉桿和CD壓桿的承載力分別按式(8)和式(9)計算:
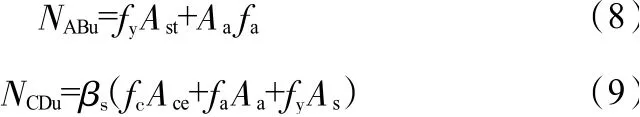
AB拉桿和CD壓桿的節(jié)點區(qū)應(yīng)分別滿足:

式中,xt、xc分別為水平拉桿、壓桿的等效寬度;βnAB、βnCD分別為AB桿、CD桿對應(yīng)的強度折減系數(shù)。
假設(shè)受拉鋼筋和受拉型鋼屈服,則由式(8)和式(10)可得:

分析表明,AD桿件內(nèi)力為零,故有FAB=FCD。假設(shè)CD桿和AB桿在節(jié)點區(qū)均達到相應(yīng)的承載力,即:

由表1可知:CCC型節(jié)點;CCT型節(jié)點,故有:
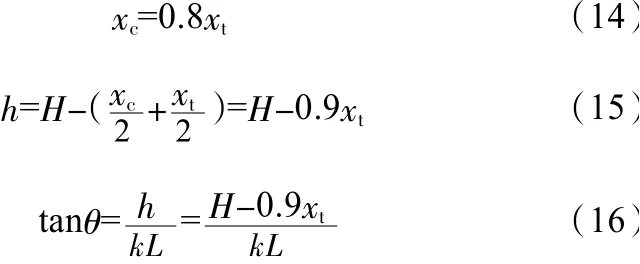
式中,H為深梁的高度;h為上下拉、壓桿中心線之間的距離;kL為集中力到支座處的水平距離;θ為斜壓桿與水平拉桿間的夾角。
2.5 模型分析
支座處受力狀況(CCT節(jié)點)如圖6所示。
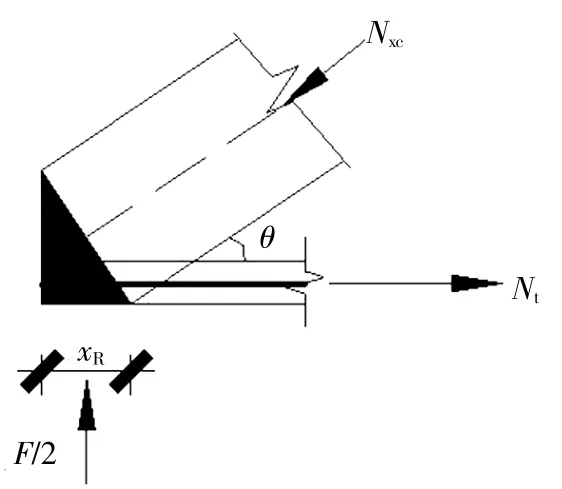
圖6 支座處受力狀況
斜壓桿有效寬度xs為:

斜壓桿承載力Nxc滿足:
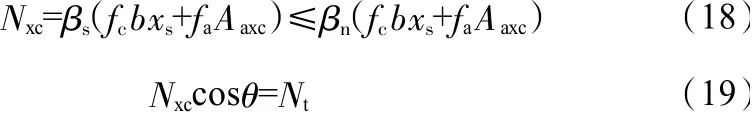
式中,Aaxc為Nxc方向的型鋼腹板截面面積。
將式(2)和式(18)代入式(19),得:
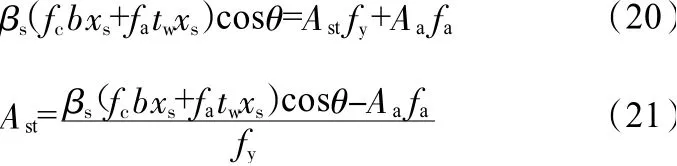
式中,tw為型鋼腹板厚度。
如果實際配置縱筋A(yù)st,a≥Ast,可以判定構(gòu)件主要發(fā)生剪切破壞;如果實際配置縱筋A(yù)st,a<Ast,可以判定構(gòu)件主要發(fā)生彎曲破壞。
2.6 承載力分析
2.6.1 彎曲破壞
當(dāng)時,受拉鋼筋和型鋼受拉翼緣達到屈服狀態(tài),按下式確定,即:

則深梁彎曲破壞時的承載力Fu計算如下:
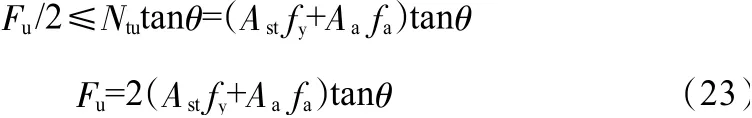
2.6.2 剪切破壞
當(dāng)Ast,a≥Ast,即受拉鋼筋未屈服時,取xt=2αs(αs為拉桿中心線到構(gòu)件受拉邊緣的距離),由節(jié)點平衡條件可得:
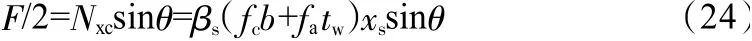
將式(7)和式(17)代入式(24),得:
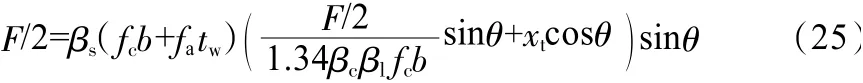
即:

對于瓶形斜壓桿,βs=0.75,代入式(26),得:
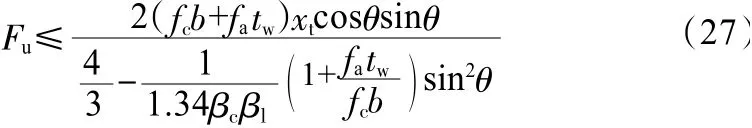
3 試驗結(jié)果對比分析
本文共搜集了25個SRC深梁的試驗數(shù)據(jù),均為集中荷載作用:其中4個為彎曲破壞,21個為受剪破壞[6-8]。分別采用YB 9082—2006《鋼骨混凝土結(jié)構(gòu)技術(shù)規(guī)程》[6](以下簡稱《鋼骨規(guī)程》)和本文提出的拉壓桿模型公式計算承載力,并與試驗結(jié)果進行對比分析,結(jié)果如表2所示。
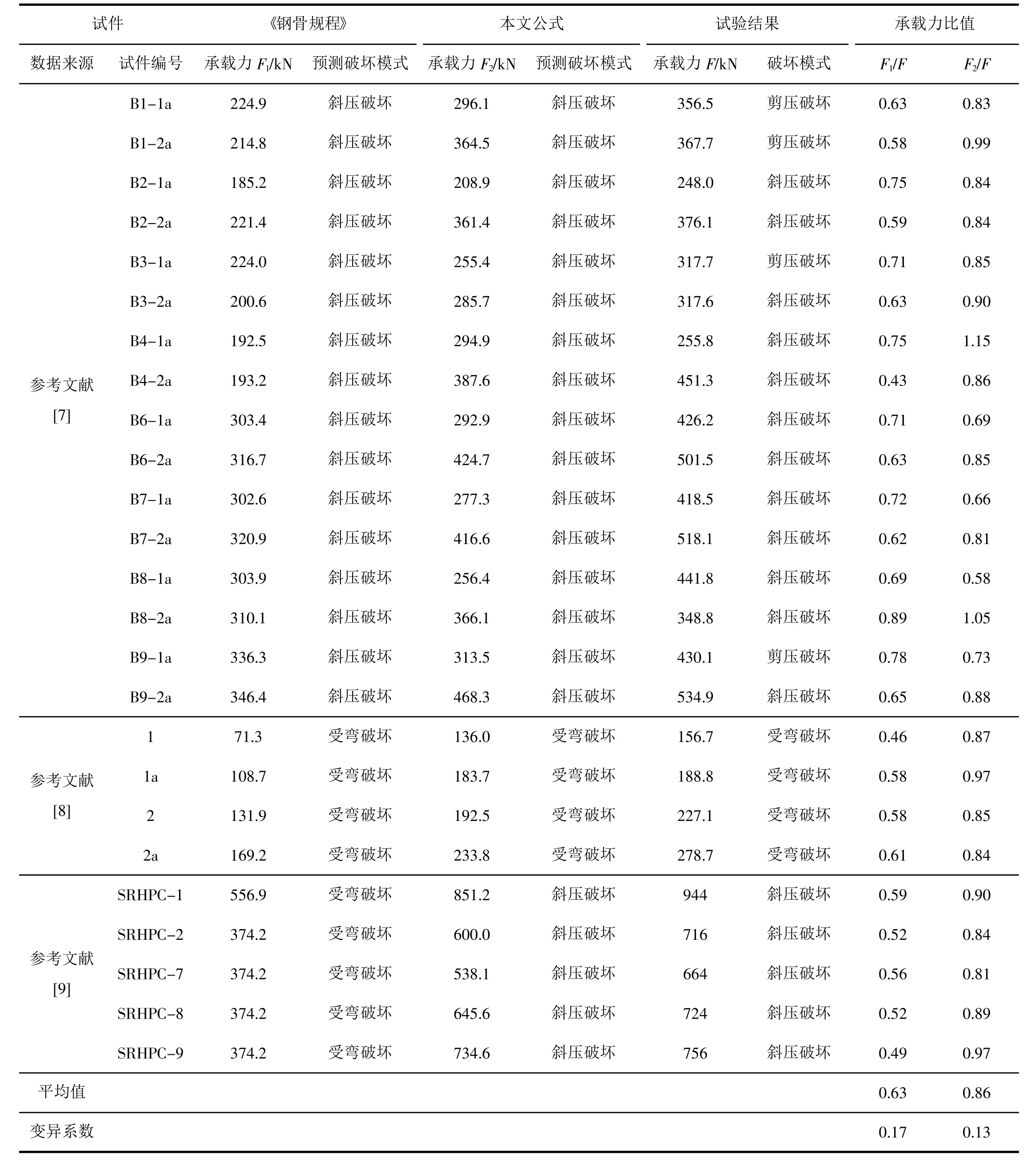
表2 承載力驗算
上述對比結(jié)果表明,《鋼骨規(guī)程》關(guān)于SRC深梁的計算公式偏于保守,變異系數(shù)也較大;而本文提出的壓-拉桿模型計算公式能較好地反映SRC深梁的極限承載力,變異系數(shù)也較小。
4 結(jié)論
我國《鋼骨規(guī)程》沒有明確的SRC深梁計算公式,而是統(tǒng)一采用平截面假定,采用一般SRC梁的計算公式。正截面和斜截面承載力設(shè)計,均是根據(jù)試驗回歸統(tǒng)計而來,缺少理論模型的支持。
壓-拉桿模型滿足塑性下限定理,是安全可靠的。根據(jù)收集到的試驗數(shù)據(jù)計算分析,采用本文提出的壓-拉桿模型的計算值與試驗值吻合較好,且離散性相對較小;《鋼骨規(guī)程》計算值比試驗值偏低較大,且離散性較大。
本文提出的壓-拉桿模型計算過程簡單,其將受力復(fù)雜的SRC深梁等效成桿系結(jié)構(gòu),以桿系結(jié)構(gòu)的受力機制代替SRC深梁實體的受力機制,能較好地反映SRC深梁的受力機制。

