瞬態熱傳導問題的精細積分邊界元法

周楓林， 袁小涵， 欽宇， 潘先云， 余江鴻

(湖南工業大學機械工程學院， 株洲 412007)

瞬態熱傳導問題存在于各種工程領域，例如機械、水利、化工、能源、航天航空等，并隨著瞬態熱傳導問題的廣泛應用，傳熱學也在迅速發展，從剛開始的理論與實驗結合的分析方法到各式各樣的數值分析方法。在實際問題中，由于結構形狀以及邊界條件的復雜性，很難獲得溫度分布的解析解[1]，數值分析方法已成為有效解決問題的方法之一。

根據傅里葉熱傳導定律，瞬態熱傳導問題通常由拋物線偏微分方程(PDF)控制。瞬態熱傳導問題最常用的數值方法是有限差分法(finite difference method，FDM)[2]，因為他在求解瞬態熱傳導問題中顯得非常自然。除了FDM外，還有發展了許多求解瞬態熱傳導問題的數值計算方法，如有限體積法(finite volume method，FVM)[3]、有限元法(finite element method，FEM)[4]、無網格法(meshless method，MM)[5-9]和邊界元法(boundary element method，BEM)[10]，其中，邊界元法是一種只涉及邊界網格化的數值計算方法，優點是可節省計算時間和存儲量，計算精度比較高，邊界區域的形狀可以任意，求解無限大區域的熱傳導問題比較理想[11]，但是因為問題的復雜程度，一般找不到問題的基本解，這時邊界積分方程中會出現與內部熱源等相關域積分。為避免域積分的直接計算，Yang等[12-13]、Feng等[14]在邊界元法中引入了徑向積分方法，將域積分轉化為邊界積分。周楓林等[15]將雙互易邊界元法運用于標量波傳播問題。Guo等[16]采用了三重互易法來避免瞬態熱傳導問題中的域積分。對于雙互易法的精度問題，黃誠斌等[17]探討了域內點的布置位置對計算精度的影響，并提出了可讓精度得到進一步提高的一種自適應布點方法。

在邊界元法的許多計算運用中，通常采用有限差分格式對時間進行離散，此時計算結果的精度與時間步長的選取有著密切的聯系[18]，雖然有限差分邊界元法是條件穩定的，但是在大時間步長上，數值結果往往不穩定。為了避免解決上述問題，Yu等[19]將精細時域展開法與雙互易邊界元法相耦合，避免了直接計算域積分；Yao等[20]將精細積分方法[21]運用于瞬態熱傳導的邊界元模型中；Yao等[22]采用精細積分邊界元法解決了雙重相變問題；陳豪龍等[23]將雙互易邊界元法和精細積分方法用于求解二維瞬態熱傳導問題。

對于雙互易精細積分方法在三維熱傳導問題上還有待深入研究。為此，提出一種雙互易法(dual reciprocity method，DRM)與精細積分法(precise integration method，PIM)相耦合的方法解決含內部熱源的三維瞬態熱傳導問題。首先將瞬態熱傳導問題視為準穩態問題，將溫度對時間的導數項視為等效熱源。通過DRM將熱源的域積分轉化為邊界積分。對空間變量進行離散后，轉化為關于域內溫度分布的初值問題，最后運用PIM解決該初值問題，在計算了域內節點的溫度后，再通過邊界積分方程計算邊界的溫度和熱通量。通過邊界元方法對結構進行熱傳導分析，給工程結構的改進提供一種數據支持，并促進邊界元分析方法在熱傳導問題方面的應用。

1 瞬態熱傳導的雙互易邊界元法

1.1 控制方程及其邊界條件

具有內部熱源的各向同性介質瞬態常系數熱傳導問題可表示為

(1)

1.2 邊界積分方程

對于瞬態熱傳導問題邊界元法，控制方程的邊界化是關鍵步驟，借助加權余量法和三維穩態熱傳導問題的基本解，將控制方程轉換為邊界積分方程，可表示為

(2)

對于三維問題有

(3)

1.3 徑向基函數逼近

雙互易邊界元法處理瞬態熱傳導問題的關鍵在于對相關項的逼近，用徑向基函數(radial basis function,RBF)對已知函數(熱源密度函數)和未知函數(與時間相關的溫度函數)進行近似表示。取徑向基函數fi(x)為

(4)

式(4)中：rdis為RBF插值點到源點的距離；s為形狀參數；i為內部節點和邊界節點數之和。

(5)

故之前所提到的已知函數和未知函數可表示為

(6)

(7)

式中：Q(x，t)為已知的與位置相關的熱源密度函數；αi(t)、βi(t)為未知系數。

系數向量β與α可表示為

(8)

F-1Q(t)=β(t)

(9)

并將式(5)、式(6)和式(7)代入式(2)可得

(10)

令：

(11)

然后與推導式(2)相類似，運用分部積分法將式(10)中的域積分轉化為邊界積分，可表示為

(12)

1.4 邊界離散

式(12)中只涉及邊界積分，所以在邊界離散后，可得到方程的離散形式為

(13)

式中：j為邊界單元個數；m為單元中的節點數，采用八節點二次面單元，m=8；xm為單元中節點的三維空間坐標；Nm為八節點面單元的形函數。

然后在每個邊界的插值點上配置場點，將上述方程寫為矩陣形式

(14)

δijC(yi)，yi∈Γ

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

將式(8)和式(9)代入式(14)可得

(24)

特別的是，由于Q(x,t)一般為已知的與位置相關的熱源密度函數，所以向量Q(t)為已知向量。

1.5 形成微分方程組

式(15)為半離散系統，將其改寫為

(25)

假設邊界類型不隨時間改變，可將邊界條件的表達式改寫為

c1u(x,t)+c2q(x,t)=c3，x∈Γ

(26)

式(26)中：c3為邊界條件；c1和c2為常數值，其值可由邊界類型來確定，則有

(27)

所有邊界節點上的邊界條件可統一表示為

(28)

然后合并式(25)和式(28)可得

(29)

則邊界溫度和邊界熱通量可表示為

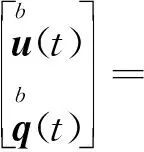
(30)

令

(31)

(32)

則式(30)簡寫為

(33)

然后考慮內部點，則有

(34)

(35)

(36)

(37)

(38)

將式(33)代入式(34)得

(39)

令

(40)

(41)

式(39)可簡寫為

(42)

式(42)為一階常系數微分方程組。

2 精細積分方法

對于式(42)的一階常系數微分方程組，可用已知的初始條件求解。

u(x,t0)=u0(x), ?x∈Ω

(43)

式(42)的通解形式為

(44)

式(44)中：τ為積分時間變量。

(45)

式(45)中：I為單位矩陣。

式(33)稱為矩陣指數函數，為使得計算成本最小，采用逐步計算的方法求解式(44)。

(46)

因而，式(46)可化簡為

(47)

這是一個代數推進方程，依據式(43)的初始條件，通過該方程計算，可以逐步得到域內溫度，在計算完域內溫度后，通過式(33)和式(39)可計算出邊界上的量。

矩陣指數函數的計算精確度決定了整個系統的一個計算精度，由于矩陣指數函數涉及大量的矩陣乘法，所以計算非常耗時，為了準確計算該矩陣指數函數，采取一種精細計算方法。

式(45)實際上可以看作是泰勒展開式，其收斂速度在很大程度上取決于時間步長。理論上，級數收斂于任意時間步長，然而，與較大的時間步長相比，較小的時間步長下，式(45)可以用很少的截斷項來計算。在精細積分方法中，矩陣指數函數中的時間步長被細分為

(48)

式(48)中：M為細分參數。

運用泰勒級數展開，可表示為

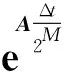
=I+Er

(49)

=(I+Er)(I+Er)

=I+2Er+ErEr

(50)

然后重新賦值Er，使得

Er=2Er+ErEr

(51)

可得

=(I+Er)(I+Er)

=I+2Er+Er×Er

(52)

然經過M次重復計算和重新賦值Er后，最終可得

eAΔt=I+Er

(53)

在整個計算過程中，Er的計算涉及了p個矩陣乘法，eAΔt的計算涉及了M個矩陣乘法，特別的是，假如時間步長為常量，那么eAΔt只會被計算一次。并且在時間步推進中，只涉及矩陣的乘法運算。

3 數值算例

為驗證所提出方法的有效性、準確性和穩定性，給出3個數值算例，運用雙互易精細積分方法獲得的計算結果與解析解進行對比。用于評估的相對誤差的表達式為

(54)

在這3個算例中，對于雙互易方法，使用的近似函數為前面所提到的式(6)，形狀參數s為1，對于精細積分方法中的細分參數M和截斷參數p，3個案例都取10和6；材料的熱導率、熱容和密度分別給定為1 W/(m·C)、1 /(kg·C)和1 kg/m-3。

3.1 狄利克雷邊界條件下的環面結構

在這個數值算例中，分析圖1所示的環形結構上的瞬態熱傳導問題，圓環的外徑和內徑分別為26 m和14 m。

狄利克雷邊界條件為

(55)

熱源項為

Q(x,t)=2 W/m-3

(56)

初始條件為

(57)

解析解為

(58)

在整個計算過程中，如圖1所示，總共劃分了750個矩形單元，2 381個邊界節點，1 473個徑向基函數插值點。

考慮0～50 s的時間段，并且選取了6個時間步長用于計算，即0.1、0.2、0.5、1.0、2.5、5 s，圖2展示了在不同的時間步長下，內部點計算溫度與解析解的相對誤差，可以看出，隨著時間的變化，相對誤差趨近于0，逐漸收斂，并且在時間步比較小的情況下，即使是接近初始時刻，計算結果也有很高的精確度。在本案例中，最佳時間步長為最小的時間步0.1 s，并且在同一時刻，相對誤差大小根據時間步長大小排序，越小的時間步，相對誤差越小。

同時，對該模型進行有限元分析，運用軟件為workbench，計算模型如圖3所示，設置單元大小為0.5 m，節點數為169 388，單元數為119 334。

此時考慮一般情況，即解析解不易求得的情況，給定狄利克雷邊界條件為

u(x,t)=60 ℃，x∈Γ

(59)

圖1 圓環邊界元模型Fig.1 Ring boundary element model

圖2 溫度的相對誤差隨時間變化情況Fig.2 Variation of relative error of temperature along time

熱源項為

Q(x,t)=1 W/m3

(60)

初始條件為

u(x,t0)=u0(x)=0 ℃，x∈Ω

(61)

在兩個模型中，取同樣的內部點A(7.927，-7.444，0.634 8)，運用相同的時間步長0.1 s，考慮0～10 s的時間段，將邊界元溫度計算結果與有限元分析溫度結果進行對比，如圖4所示。

圖3 圓環的有限元模型Fig.3 Finite element model of ring

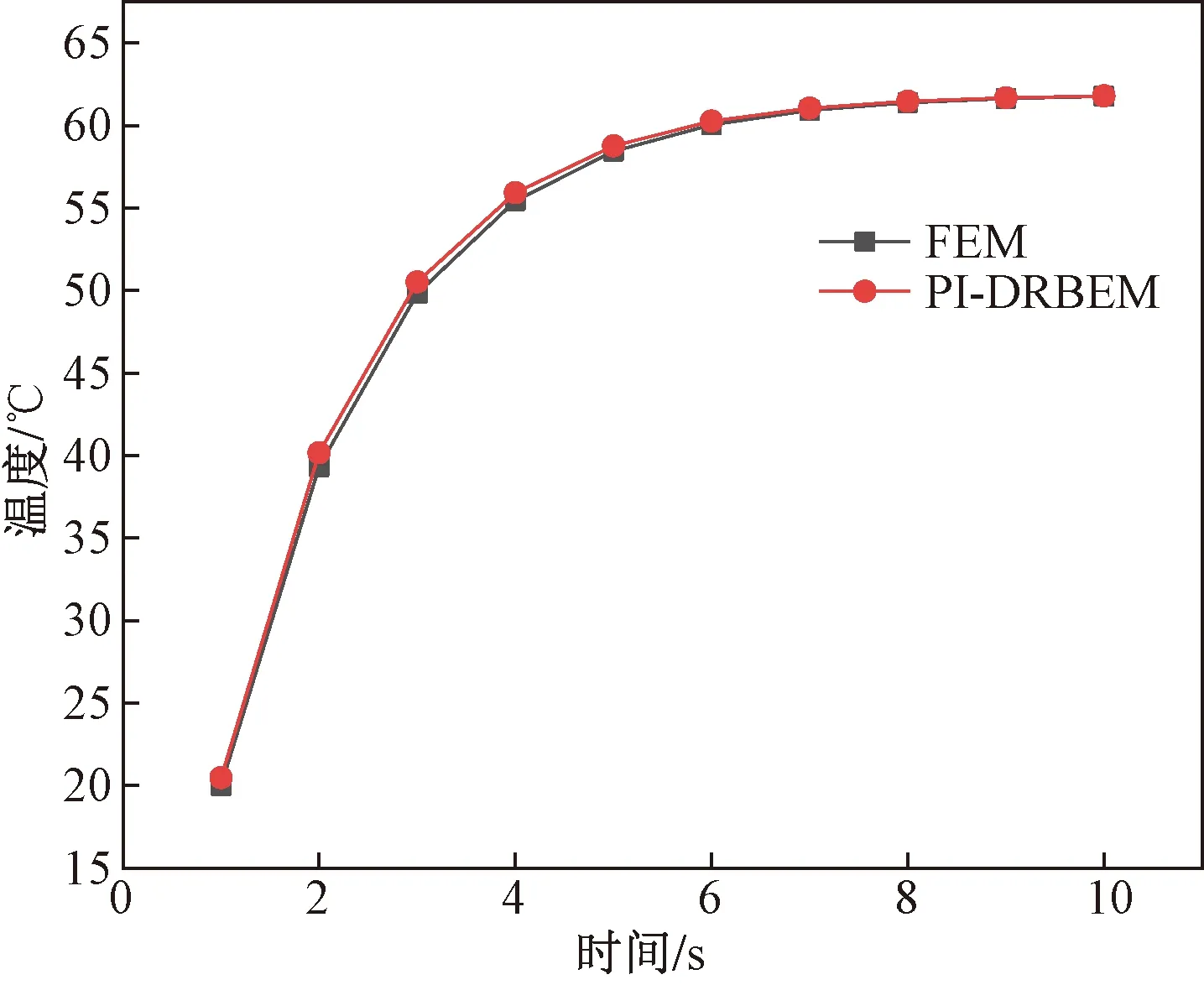
圖4 PI-DRBEM與FEM結果比較Fig.4 Comparison of results between PI-DRBEM and FEM

圖4表明，雙重互易法和精細積分法耦合擁有很高的精度，論證了該方法的有效性和準確性。

3.2 混合條件下的山型結構

此算例考慮在混合邊界條件下，一個山型結構的瞬態熱傳導問題，三維模型及其尺寸如圖5所示。邊界劃分如圖6所示。

圖5 山型結構幾何示意圖Fig.5 Geometric diagram of mountain structure

Γ1和Γ2為諾依曼型邊界圖6 邊界劃分幾何示意圖Fig.6 Geometric diagram of boundary division

邊界條件為

(62)

q(x,t)=62x2+16t，x1,x2,x3∈Γ1

(63)

其余邊界Γ3為狄利克雷型邊界，邊界條件為

8t(x1+2x2+1.5x3)

(64)

熱源項為

Q(x,t)=2x1+4x2+3x3

(65)

初始條件為

u(x,t0)=u0(x)

(66)

解析解為

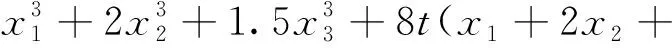
1.5x3)，x1,x2,x3∈Ω

(67)

在此算例的計算中，總共劃分了500個連續的隨機四邊形單元，1 920個邊界節點，164個徑向基函數插值點。使用不同的時間步長來驗證方法對時間變量的收斂性,相對誤差結果如圖7所示。

在本算例中，考慮同樣的6個時間步長，在混合邊界條件下，時間步長趨近于0時，計算結果從一開始就具有很高的精度。稍大的時間步長中，盡管剛開始誤差偏大，但隨著時間的推移，相對誤差快速減小。可以看出，雙互易精細積分法的精確性和有效性。

3.3 狄利克雷邊界條件下的彎管結構

此算例考慮空心彎管結構，模型結構及尺寸如圖8所示。所有表面為狄利克雷邊界，其條件為

圖7 溫度的相對誤差隨時間變化情況Fig.7 Variation of relative error of temperature along time

R為半徑圖8 彎管幾何結構示意圖Fig.8 Geometric diagram of elbow

(68)

熱源項、初始條件、解析解與算例2保持一致。在整個計算過程中，總共劃分了448個矩形單元，1 718個邊界節點，326個徑向基函數插值點，插值點分布如圖9所示。

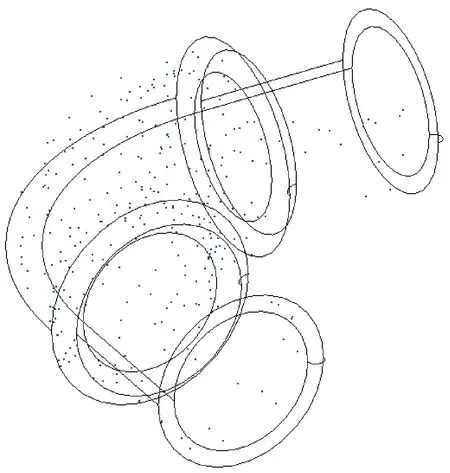
圖9 彎管RBF插值點分布Fig.9 Distribution of RBF interpolation points of elbow

在本算例中，同樣考慮0～50 s時間段，結果如圖10所示，可以看出，相對誤差在任何一個時間步中都是隨著時間推移而減小，并且時間步長取0.1 s時，內部點熱通量計算結果的相對誤差最小，并且在初始時刻附近也具有較小的相對誤差。有趣的是，內部點熱通量的計算精度，并不是隨著時間步長減小而變高，在選取的6個時間步中，在取中間大小的時間步1.0 s時，相對誤差在任何時刻都是最大的。

圖10 熱通量隨時間的相對誤差變化Fig.10 Relative error variation of heat flux along time

4 結論

提出了求解含有內部熱源的三維瞬態熱傳導問題的雙互易精細積分方法。在處理該熱學問題中，首先運用雙互易法處理域積分，再利用精細積分方法處理所得到的初始條件問題。得出如下結論。

(1)雙互易邊界元法和精細積分方法的耦合具有較高的精度和穩定性。

(2)對于不同的結構體和邊界條件，并不是時間步長越小越好。存在時間步長減小，但是計算結果的相對誤差卻增大的情況，但通常情況下，時間步長越接近零，越有可能獲得高精度結果。

(3)在無解析解的情況下，該方法依舊有很高的精確性。

不足是該方法的計算效率有待進一步提高，特別的是，在第一個時間步內，需要進行大量的矩陣與矩陣的乘法運算及矩陣求逆運算。而在后續時間步中，只需進行已有矩陣與向量的乘法運算，容易實現并行計算。