啟發式狼群算法求解不相關并行機調度問題

荀洪凱，陶翼飛，羅俊斌，何 李

（1.昆明理工大學機電工程學院，云南昆明 650504；2.昆明昆船邏根機場物流系統有限公司，云南昆明 650236）

0 引言

并行機調度［1］（Parallel Machine Scheduling，PMS）在生產制造領域應用廣泛，如半導體加工、注塑成型加工、紡織加工、光刻加工、卷煙加工等，并行機調度問題也已經被證明為一類經典的NP-hard 問題。而在實際生產加工過程中，由于并行機加工能力不同，需要考慮工件加工分配問題，導致其復雜程度更高，求解難度更大，從而對不相關并行機調度（Unrelated Parallel Machine Scheduling，UPMS）問題的研究具有更重要的理論意義和應用價值。

近年來，不相關并行機調度問題被廣泛研究，目前并行機調度問題大多采用啟發式算法或其它智能優化算法進行求解。通過改進傳統智能優化算法進行求解仍然是重要的研究方向，例如對遺傳算法的改進方面，Abreu 等［2］提出一種混合遺傳算法用于解決具有序列相關設置時間的不相關并行機調度問題；Xuan 等［3］將遺傳算法和模擬退火算法結合，開發了一種新的遺傳模擬退火算法，以解決具有不相關并行機的混合流水車間調度問題。近年來，不少新算法相繼被提出，蟻獅優化算法［4］、混合差分進化算法［5］、混合多目標教—學優化算法［6］、混合啟發式算法［7］等，都被應用到求解并行機調度問題。同時，很多組合優化算法也被提出，Zhang 等［8］提出一種結合列表調度、啟發式最短設置時間優先規則和最早完成時間優先規則的組合進化算法以解決具有有限工人資源和學習效應的不相關并行機調度問題。從當前研究可以看出，通過算法融合，以及有針對性地提出一些新算法，可以有效彌補傳統算法所存在的不足，并且為求解不相關并行機調度問題擴展了研究方向，本文提出一種算法融合的方式以優化并行機調度問題。

目前，針對不相關并行機調度問題的研究已經比較成熟，但在搜索效率方面并未得到實質性提升，代招等［9］通過利用混沌映射和反向學習策略生成初始種群，改善初始種群的質量，求解以最小化最大完工時間為目標的柔性作業車間調度問題；顧文斌等［10］提出一種新的啟發式算法提升初始種群質量，改善搜索效率。目前，不相關并行機調度問題中搜索效率提升方法相關研究較少。在算法選擇方面，吳虎勝等［11］提出一種狼群算法（Wolf Pack Algorithm，WPA），該算法利用不同的搜索機制對狼群進行搜索，結構簡單、尋優效率高，主要應用在多旅行商問題［12］、柔性作業車間調度問題［13］以及置換流水車間調度問題［14］中。目前，狼群算法已經解決了多種調度問題，但在并行機調度問題中的研究并不完善。本文設計啟發式算法旨在提高其搜索效率，選用狼群算法目的是保留算法并行性等優勢。

綜上所述，本文在求解不相關并行機調度問題時以最小化最大完工時間為優化目標，首先，為提高搜索效率，提出一種啟發式算法，選擇合適的工件分配原則，將啟發式算法得到的種群與隨機生成的初始種群共同進行優化；其次，結合狼群算法的顯著特點以及在求解調度問題方面的優勢，對狼群算法智能行為機制中鄰域搜索方式進行設計，局部鄰域搜索與全局鄰域搜索相結合，使搜索效率達到最大化，最終通過不同規模不相關并行機調度問題算例進行仿真優化實驗，證明所提出的啟發式狼群算法（Heuristic Wolf Pack Algorithm，HWPA）求解不相關并行機調度問題切實有效，與其它優化算法相比該算法擁有更高的求解效率和精度。

1 問題描述

本文研究不相關并行機調度問題，該問題可以描述為：設N為待加工工件集合，M為并行機機器集合，每個工件只需在一臺機器上加工，同一臺機器在同一時間只能加工一個工件，并且每個工件在每臺機器上加工時間不同，每個工件之間沒有先后順序約束，即所有工件具有相同的優先加工級，每個工件被加工的概率相同。假設工件j在機器i上的加工時間為t(i，j)，定義工件j在機器i上的廣義加工時間為x(i，j)t(i，j)，其中x(i，j)=1 時表示工件j在機器i上加工，否者x(i，j)=0。定義工件j在機器i上的加工初始時間為T(i，j)，工件j+1 在機器i上的加工初始時間為T(i，j+1)。總完工時間用C表示，最終求解目標為最小化最大完工時間，即minCmax。并行機調度示意圖見圖1。

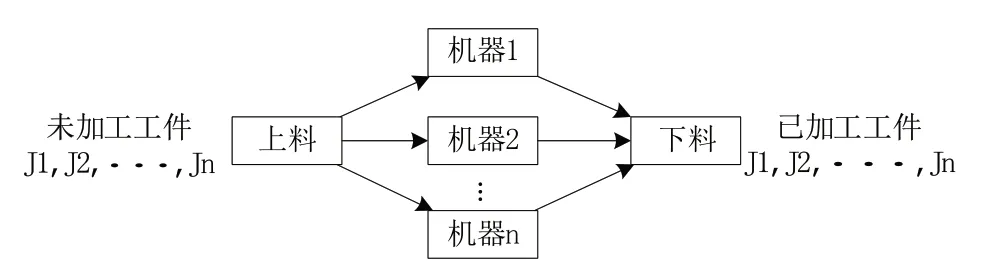
Fig.1 Parallel machine scheduling schematic圖1 并行機調度示意圖

目標函數為：

約束條件為：

式（1）為模型中最小化最大完工時間，即目標函數；式（2）確保每個工件只能由一臺并行機完成加工；式（3）定義了變量的取值范圍，式（4）規定工件在機器上加工未完成時不能更換工件；式（5）保證每臺機器上的工件按照一定的順序進行加工。

2 啟發式狼群算法

為有效求解不相關并行機調度問題，本文提出一種啟發式狼群算法。該算法主要由兩部分組成：①針對不相關并行機調度的特點，對算法初始種群通過啟發式算法進行調整；②在迭代過程中，不同類型的狼群設置不同的鄰域搜索方式。算法流程如圖2所示。

具體步驟如下：①設定啟發式算法中每代個體數i、規模數及迭代次數i；②初始化種群，將隨機初始化的種群與啟發式算法尋優得到的種群共同組成初始種群；③狼群分類，對初始化種群中的所有個體進行譯碼、仿真并計算其適應度值，按照計算出的適應度值以及選定的規模數進行相應分類；④探狼游走，分類后的個體中探狼個體根據下文游走機制進行相應的鄰域搜索，并計算其適應度，觀察最優解是否得到更新；⑤頭狼召喚，分類后的猛狼個體根據召喚機制進行相應的鄰域搜索，計算搜索后的個體適應度，判斷最優解是否需要更新；⑥狼群圍攻，將最優個體以外所有個體根據圍攻機制進行全局鄰域搜索，計算出本次迭代中所有個體適應度值并找到最優解；⑦判斷最大迭代次數是否完成，若是，則算法結束，輸出最優個體編碼即為最優解，若否，則執行步驟③。

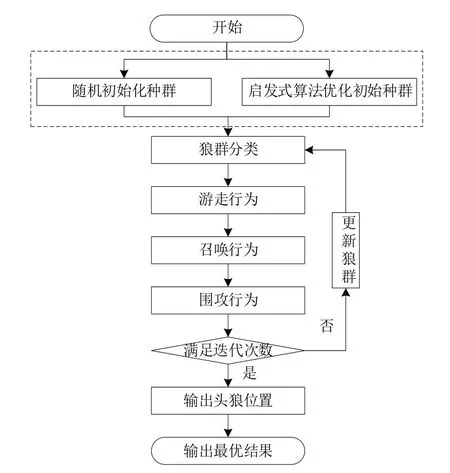
Fig.2 Flow of HWPA圖2 啟發式狼群算法流程

2.1 初始種群生成

在狼群優化算法中，如果僅用隨機方式生成初始種群，將增加種群迭代次數，因此本文在初始化種群時提出新的啟發式算法，流程如圖3所示。

Fig.3 Flow of heuristic algorithm圖3 啟發式算法流程

mint(i，j)表示工件i在機器j上的最短加工時間，用jmin表示加工時間最短的機器，用jmax表示加工時間最長的機器，Nj表示機器j上加工工件集合，Njmax表示加工時間最長的機器上所加工工件集合。tj表示工件i在兩臺機器上加工時間差值。

式（6）表示機器j的總加工時間，式（7）表示加工時間最長機器的加工時間，式（8）表示工件i在總加工時間最長的機器和總加工時間最短的機器上加工時間差值最小，其中i∈Njmax。

啟發式算法流程如圖3 所示，具體步驟如下：①分別選出加工工件時間最短的機器；②確定jmin和jmax，計算出t(jmax)即是此時總完工時間；③根據式（6）和式（7）找到Njmax，并根據式（8）找到可以替換加工機器的工件i并進行替換；④重新計算總完工時間，判斷總完工時間是否減少，若總完工時間減少則進行工件替換，并重復步驟②至④，若總完工時間增加則停止運行算法。

給出一個示例進行說明，先為每個工件選擇加工時間最短的機器，此時甘特圖如圖4所示。

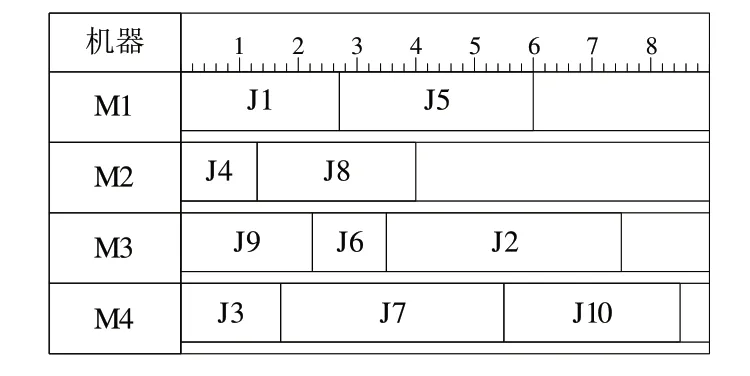
Fig.4 10×4 Gantt chart before adjustment圖4 10×4調整前甘特圖

根據仿真后的結果，找到最早和最晚完工機器，考慮將M4 上的工件轉移到M2 機器上進行加工，此時可以選擇的工件有J3、J7、J10。如圖5 所示，根據這3 個工件在M2和M4 上加工所用的時間差決定將增量最小的工件J3 分配到M2上加工。

Fig.5 Time increment before and after adjustment圖5 調整前后時間增量

最終調整后得到如圖6 所示甘特圖，此時總的完工時間減少，可以繼續進行調整，直到總的完工時間不再減少為止。

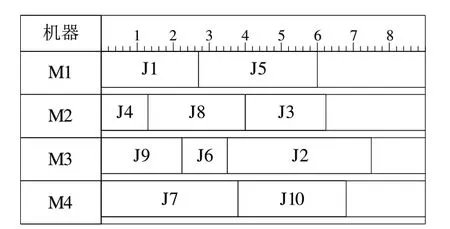
Fig.6 10×4 adjusted Gantt chart圖6 10×4調整后甘特圖

2.2 編碼及譯碼

本文采用單鏈編碼方式，首先用工件編號給出工件的加工順序，其次用大于工件編號的數字將排好的加工順序進行分隔，進而確定工件的加工機器。這種編碼方式能夠使編碼更簡潔，減少計算次數。

根據編碼方式，譯碼步驟為：①將分隔數字找出；②確定工件加工順序，同時將工件分配到相應待加工機器。

例如：在7 個工件，3 臺并行機的加工過程中，編碼［5 7 3 8 4 2 9 6 1］中數字8 與數字9 代表分隔數字，工件加工順序為編碼先后順序。并行機1 加工工件5、7、3，并行機2加工工件4、2，并行機3加工工件6、1。

2.3 種群適應度

本文研究的是以最小化最大完工時間為目標的不相關并行機調度問題，用時越少，適應度越高，因此種群的適應度f用所有工件加工完成時間的倒數擴大100 倍代替，即：

2.4 智能行為設置

根據狼群算法以及不相關并行機調度的特點，設計新的智能行為機制。

（1）選擇機制。在迭代過程中，迭代后的最優個體優于迭代前最優個體，則進行更新。

（2）游走機制。針對種群中部分次優個體種群進行鄰域搜索。將種群中除最優個體以外的其他個體進行適應度排序，將部分適應度較好的個體看作探狼，并在其鄰域內進行隨機搜索。為了提高種群多樣性，防止種群陷入局部最優解，本文對次優種群的步長沒有作具體規定，每段編碼中隨機找一段編碼，將這段編碼位置進行隨機調換。如圖7 所示，位置編碼為［5 7 3 8 4 2 9 6 1］，執行游走行為時，隨機選擇的片段為［7 3 8 4 2］，隨機排序后的片段為［2 8 3 4 7］，則隨機游走后的位置編碼為［5 2 8 3 4 7 9 6 1］，利用隨機游走方式增加了種群多樣性。

（3）召喚機制。首先，隨機選擇某一機器上所有工件并找出這段編碼，如圖8 所示，頭狼個體編碼為［5 7 3 8 4 2 9 6 1］，猛狼個體編碼為［4 1 3 8 6 7 5 9 2］，隨機選擇的并行機為2；其次，選擇剩余個體與最優個體的編碼片段對應位置進行交叉，并且剩余位置編碼用部分映射交叉，對應編碼位置在第4 位，將這段編碼與猛狼個體編碼相應位置進行部分映射交叉，交叉調整后的猛狼個體編碼為［5 1 3 8 4 2 9 6 7］，將新的編碼進行譯碼計算出適應度，若調整后的適應度優于原編碼適應度，則將原編碼進行替換。這種交叉方式能夠保留在某一臺并行機所選擇的加工工件，從而保留了較優的排序片段。

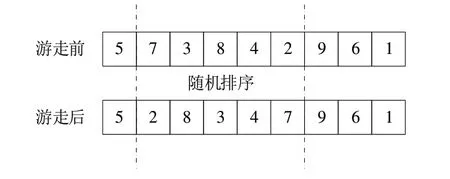
Fig.7 Wandering schematic圖7 游走示意圖

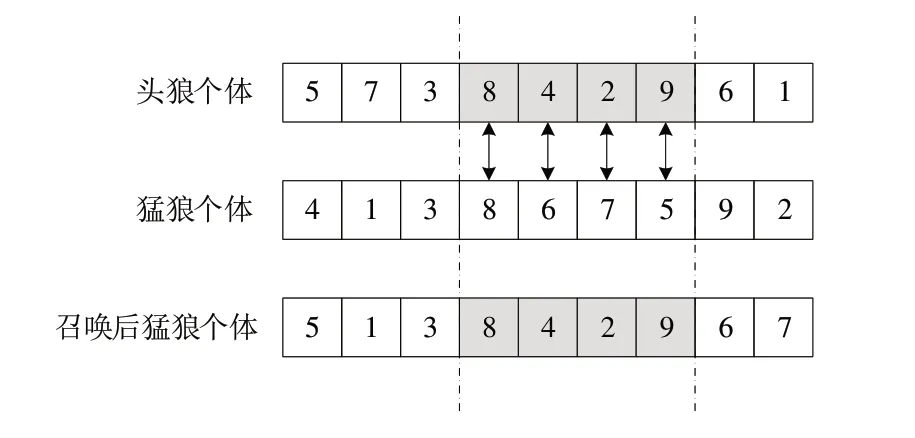
Fig.8 Calling schematic圖8 召喚示意圖

（4）圍攻機制。將最優個體編碼與次優個體編碼進行比較，相同位置的編碼將保留，如圖9 所示，最優個體編碼為［5 7 3 8 4 2 9 6 1］，其他個體的編碼為［6 7 3 4 8 2 9 5 1］，比較后發現編碼7、3、2、9、1 是相同位置相同編碼，這些編碼不發生變化，其他位置編碼采用隨機方式重新進行編碼。圍攻時的位置已經接近本次迭代最優位置，采用隨機方式進行鄰域搜索，增加解的多樣性，有利于跳出局部最優解。

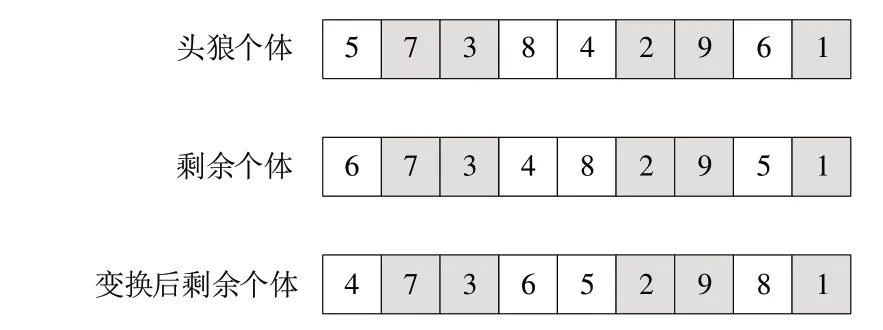
Fig.9 Besieging schematic圖9 圍攻示意圖

3 實驗設計仿真建模與分析

3.1 仿真建模

針對本文所提出算法，先用一個標準算例驗證算法有效性，然后通過遺傳算法和混合果蠅算法對不同規模算例進行仿真實驗，驗證其優越性。利用Plant Simulation 軟件建模仿真分析、Simtalk2.0 語言進行編程，建立優化算法模型如圖10所示。

3.2 算法參數設置

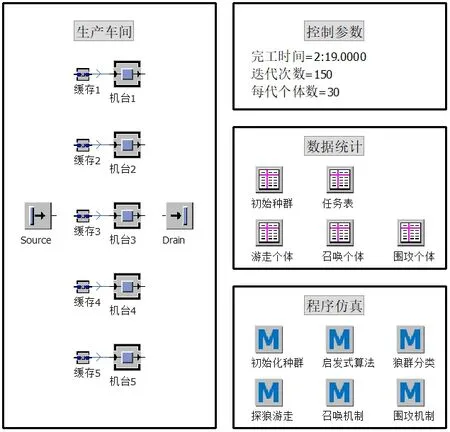
Fig.10 Modeling of 5 parallel machine scheduling for 30 workpieces圖10 30工件5臺并行機建模

啟發式狼群算法主要參數有：工件數N，并行機機器數M，迭代次數D以及每迭代一次保留的個體數即種群規模G，各參數取值如表1 所示。根據算法主要參數找到L16（45）正交表設計正交實驗如表2所示。

Table 1 HWPA parameters and values of each level表1 HWPA參數及各水平取值

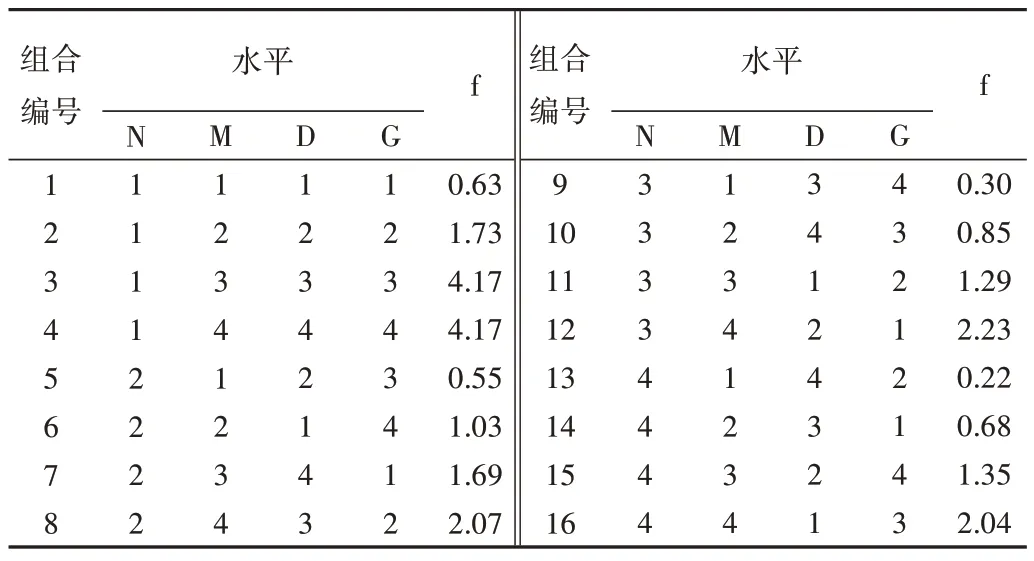
Table 2 Orthogonal table and fitness value of HWAP parameters表2 HWPA參數正交表及適應度值

通過正交實驗結果如表3 所示，繪制相應參數對算法影響水平趨勢圖，如圖11所示。

比較各參數對所求結果適應度的影響。通過圖11 可以看出，工件數目越少，適應度越好，并行機數目越多，適應度越好，算法迭代次數在150 時最好，狼群規模在30 左右能達到最優。根據正交實驗結論設計實驗參數D=150，G=30。

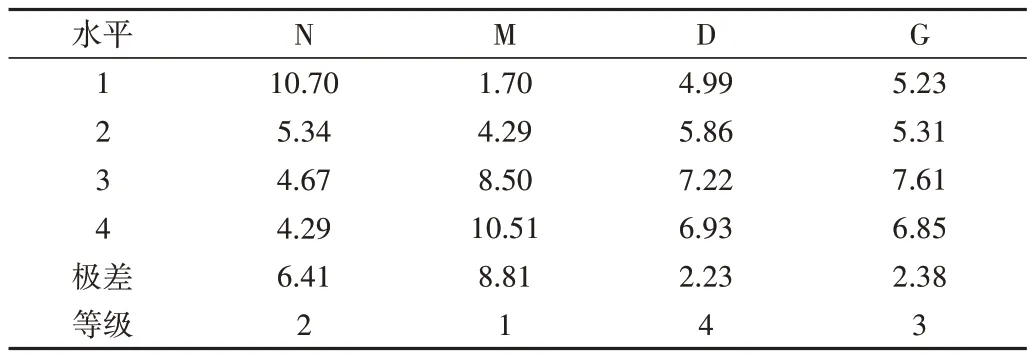
Table 3 Average fitness values of HWPA parameters表3 HWPA各參數平均適應度值

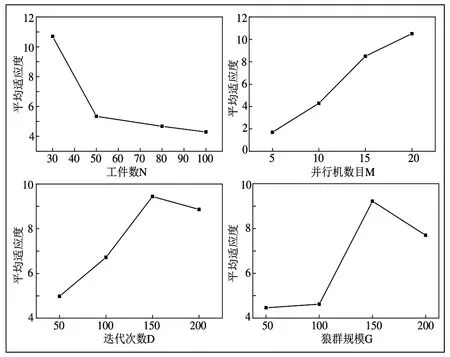
Fig.11 Trend of influence level of each factor on algorithm圖11 各因素對算法影響水平趨勢

3.3 有效性驗證

本文用一個已知實例［15］驗證啟發式狼群算法有效性，仿真中的初始化參數為：D=150，G=30，探狼規模為種群規模的50%。利用軟件仿真建模，編寫算法程序，進行50 次仿真，求取仿真平均值，得到最優結果甘特圖如圖12所示。

仿真實驗得出的最小化最大加工時間為7，與文獻中結果相同，證明本文提出的啟發式狼群算法有效。

Fig.12 Gantt chart of optimal solution of 8×4-problem圖12 8×4問題最優解甘特圖

3.4 不同規模實驗比較

為了多方位驗證算法有效性，設計不同規模的實驗與遺傳算法和混合果蠅優化算法進行比較。實驗數據來自文獻［16］。通過查閱文獻［17-20］設置參數如下：N=｛30，50，80，100，120｝，M=｛5，10｝，每組規模進行20 次實驗，每個實例迭代次數150 次，每一代的種群規模數為30，遺傳算法交叉概率0.9，變異概率0.1，混合果蠅算法的種群規模和最大迭代次數與其他算法一致，果蠅搜索半徑為［-5，5］隨機數，啟發式狼群算法探狼數量為種群數量的50%。每組規模的實驗結果如表4所示。

表4 中，IR1 表示目標函數值較GA 改進百分比，IR2 表示目標函數值較FOA 改進百分比。不同規模問題每一次迭代后的最小化最大完工時間點線圖如圖13所示。

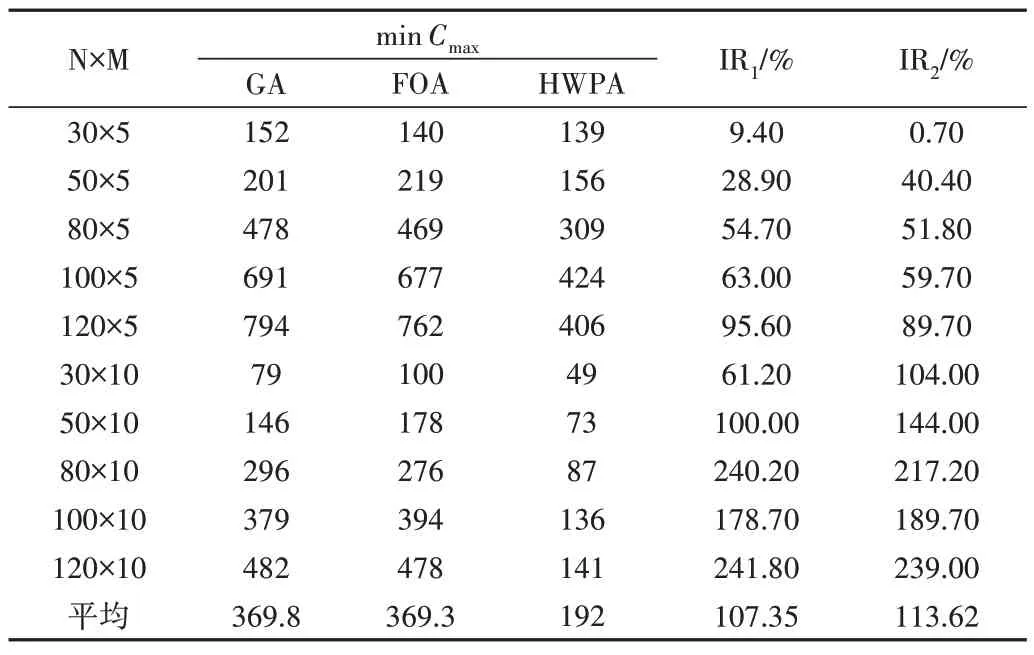
Table 4 Test results of different scale problems表4 不同規模問題測試結果

3.5 實驗結果分析

通過實驗比較可以看出，啟發式狼群算法相比其他兩種算法能得到較優結果，由于對初始種群進行了改進，啟發式算法為每個工件選擇了加工時間最短的機器，并通過改變最大完工時間機器上的工件分配，從而使該HWPA 在迭代初期就能表現出其優勢。在GA 與FOA 搜索過程中，若增加迭代次數最終也能搜索到與HWPA 接近的結果，但搜索效率會降低。在150 次迭代搜索范圍內，不同規模算例實驗結果顯示，HWPA 的目標值較GA 平均改進了107.35%，較FOA 平均改進了113.62%，精度提升較高，即使問題規模改變，啟發式狼群算法也能夠使計算結果達到相對最優值，具有較好的魯棒性。通過對智能行為機制的改進，使得每一次迭代后的最優解中保留了較優的工件分配片段。同時，采用隨機分配方式進行調整，增加了跳出局部最優解的可能，進一步使最終尋優結果達到較為滿意的程度。

從點線圖中可以看出，小規模不相關并行機調度中最小化最大完工時間相差不大，隨著工件數量與機器數目增多，3 種算法在150 次迭代后完工時間差值增大，在并行機數目保持不變的情況下，工件數目越多，啟發式狼群算法的優勢也越明顯，說明啟發式狼群算法對解決以最小化最大完工時間為目標的大規模不相關并行機調度有其優勢。

4 結語

本文針對不相關并行機調度問題，提出一種啟發式狼群算法，通過啟發式算法改變部分初始種群的選擇方式，同時根據該問題特點，對狼群算法智能行為機制重新進行設計。通過仿真優化實驗證明該算法有效，同時設置不同規模算例實驗，在一定迭代次數內，本文所提算法能有效優化最大完工時間，且求解問題規模越大優化效果也越明顯，為不相關并行機調度問題研究提供了一定參考價值。未來將繼續研究該算法在多目標并行機調度問題中的應用。

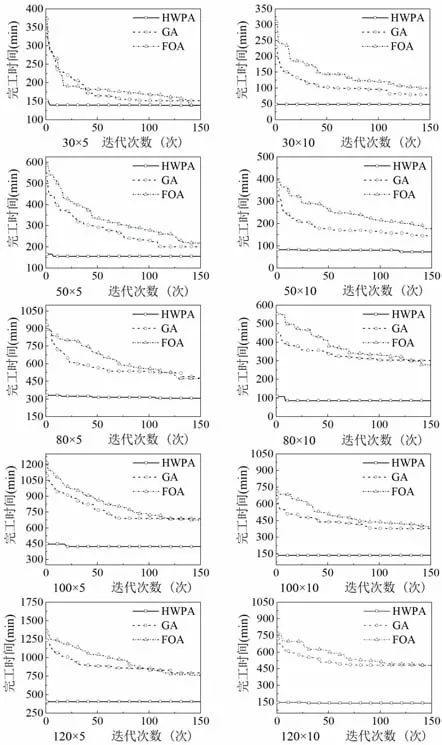
Fig.13 Optimal solutions of different scales圖13 不同規模最優解