PMSM新型積分快速終端滑模控制
諸德宏,周振飛
(江蘇大學電氣信息工程學院,江蘇鎮江 212013)
0 引言
永磁同步電機(Permanent Magnet Synchronous Motor,PMSM)因結構簡單、損耗低、功率密度高等優點在社會生產生活中受到廣泛關注與應用,但PMSM 是一個非線性、強耦合的復雜電磁動作系統,在實際運行過程中往往會出現參數攝動、負載波動、外部干擾等問題。
傳統PI 和滑模控制已無法滿足當今工業社會日益增長的高性能控制需求[1-3]。隨著現代控制理論的發展,國內外學者先后提出了許多優秀的控制方法。例如,自抗擾控制[4-6]、模糊控制[7-10]、滑模控制(Sliding Mode Control,SMC)等。
文獻[11-13]提出一種新型的指數趨近律,通過克服常規滑模控制的固有抖振問題以提高趨近速度。Kang等[14]設計一種雙冪次趨近率,改善系統在趨近模態中的動態品質。文獻[15-16]設計滑模觀測器采集PMSM 的轉速與轉子角度信息。張曉光等[17]提出混合非奇異終端滑模控制策略,結合線性滑模和非奇異終端滑模以解決非奇異終端滑模收斂速度慢的問題。周碩等[18]提出一種PMSM非奇異快速終端滑模控制(Nonsingular Fast Terminal SMC,NFTSMC)策略,能夠全局快速收斂狀態變量。李政等[19]通過在常規滑模面中加入狀態變量的積分項,設計了一個PMSM 積分型滑模速度控制器,雖能消除穩態誤差,但積分Windup 效應會使消除穩態誤差的時間過長,系統性能有所下降。王鑫等[20]提出一種高階積分滑模控制器,在減弱抖振現象的同時增強了系統的魯棒性。
為進一步提高PMSM 調速系統的控制性能,本文提出新型積分快速終端滑模控制(New Integral FTSMC,NIFTSMC)方法。該方法在快速終端滑模控制的基礎上引入積分型滑模控制思想,在繼承快速終端滑模快速性的同時,通過重新設計積分項避免傳統積分型滑模的積分Windup效應。
1 新型積分快速終端滑模控制策略
選用快速終端滑模面結合積分型滑模控制思想,將非線性函數與模糊量的積分形式引入滑模面,提出一種新型積分型快速終端滑模控制面,具體數學表達式如式(1)所示:

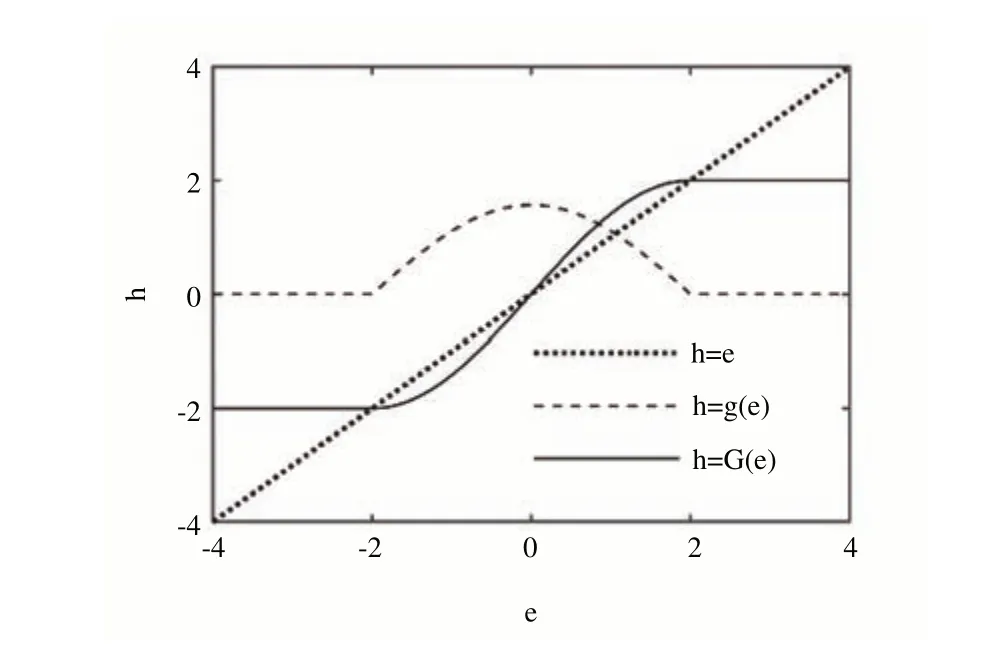
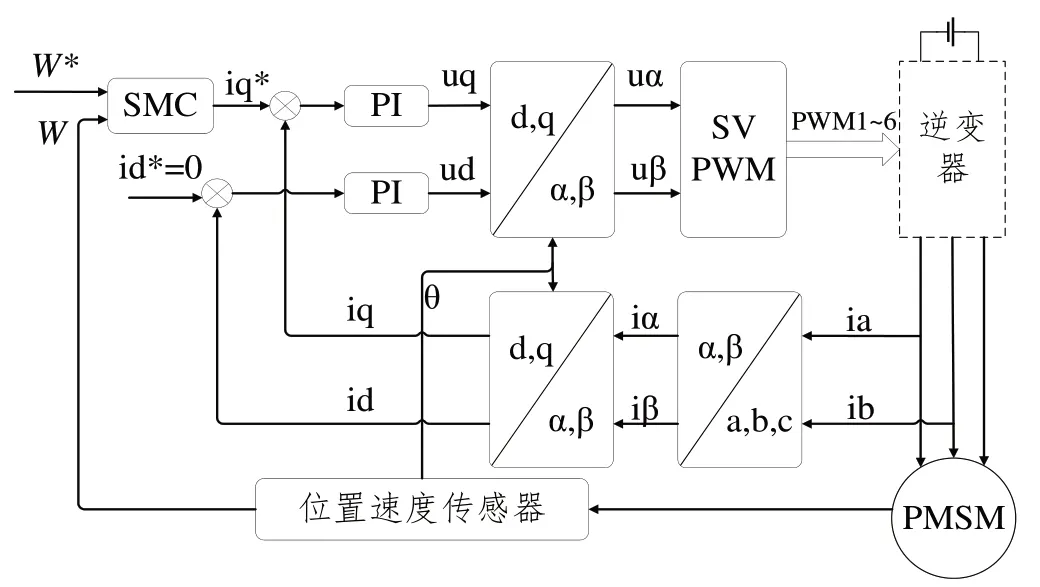
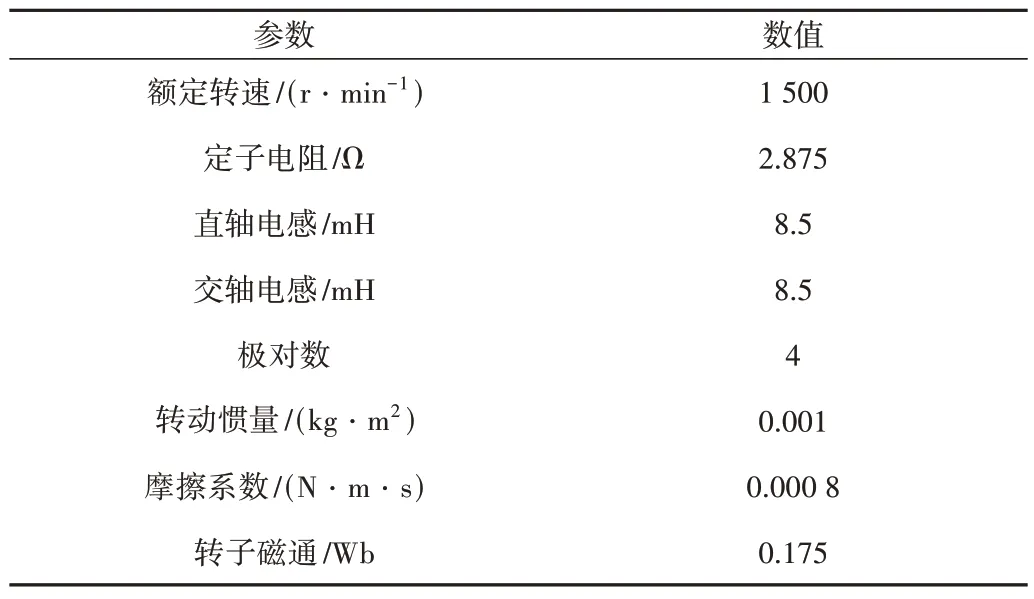
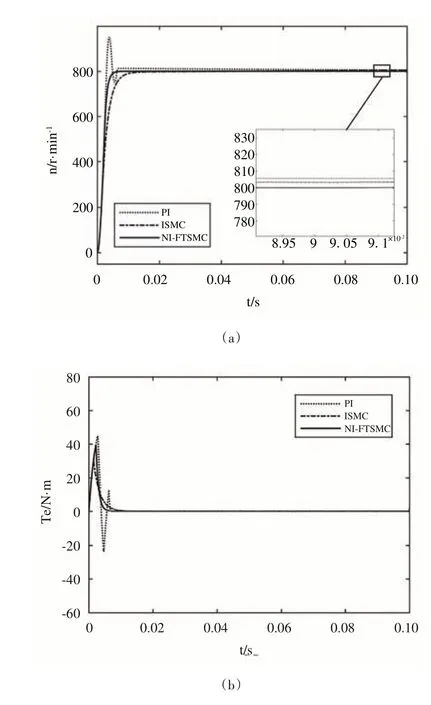
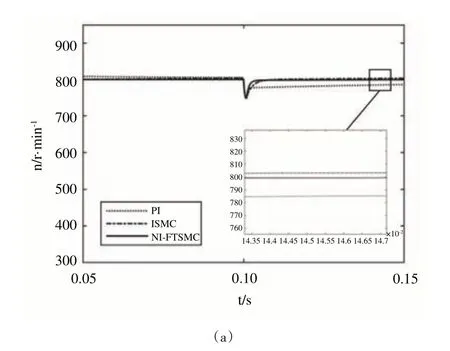
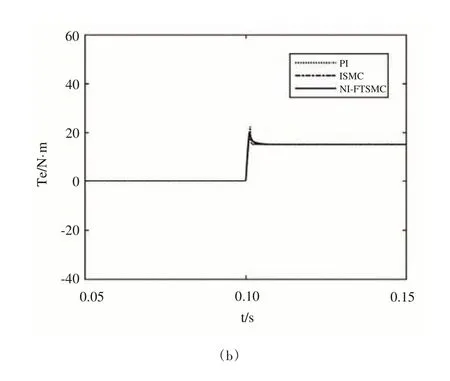
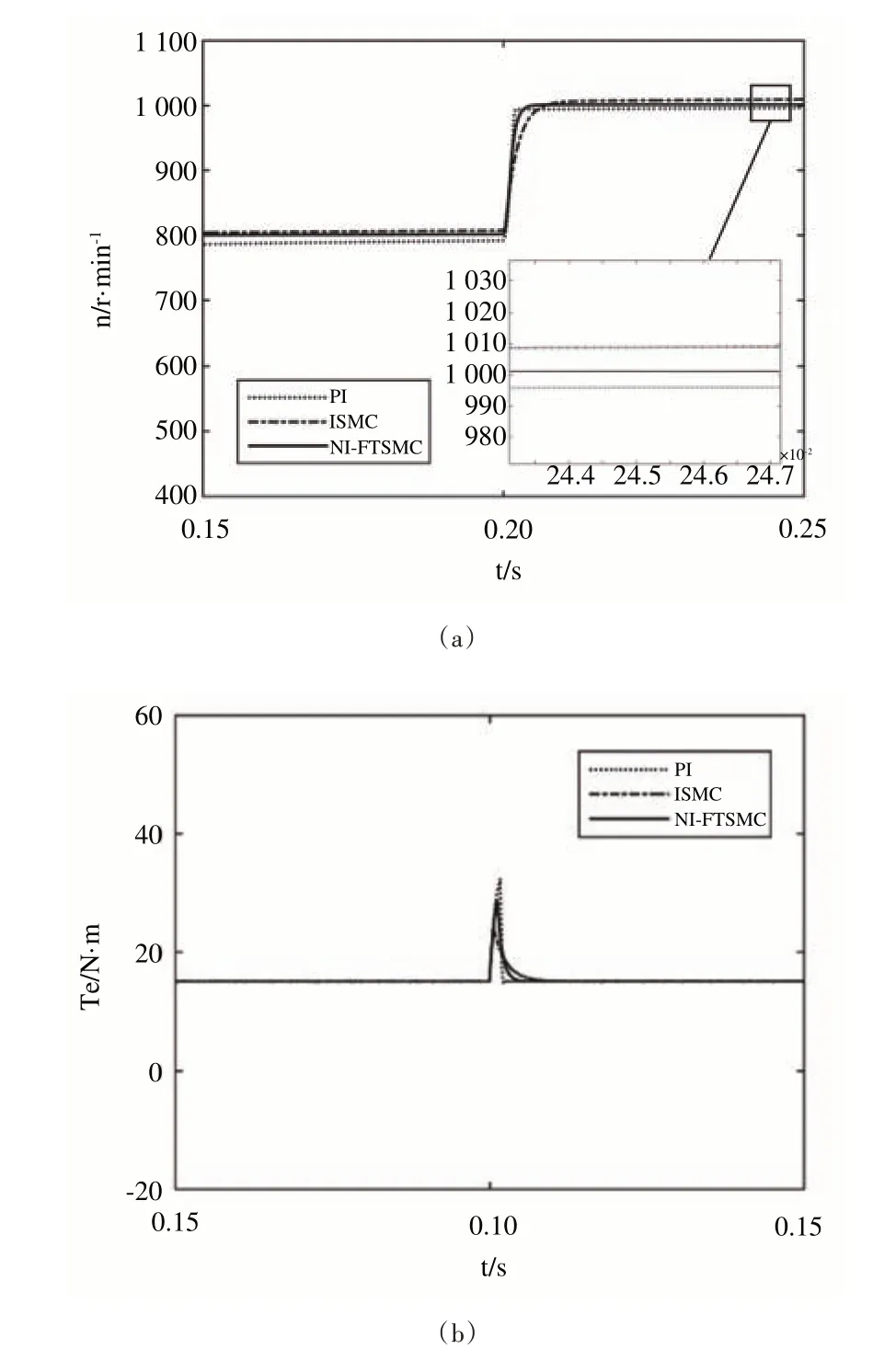
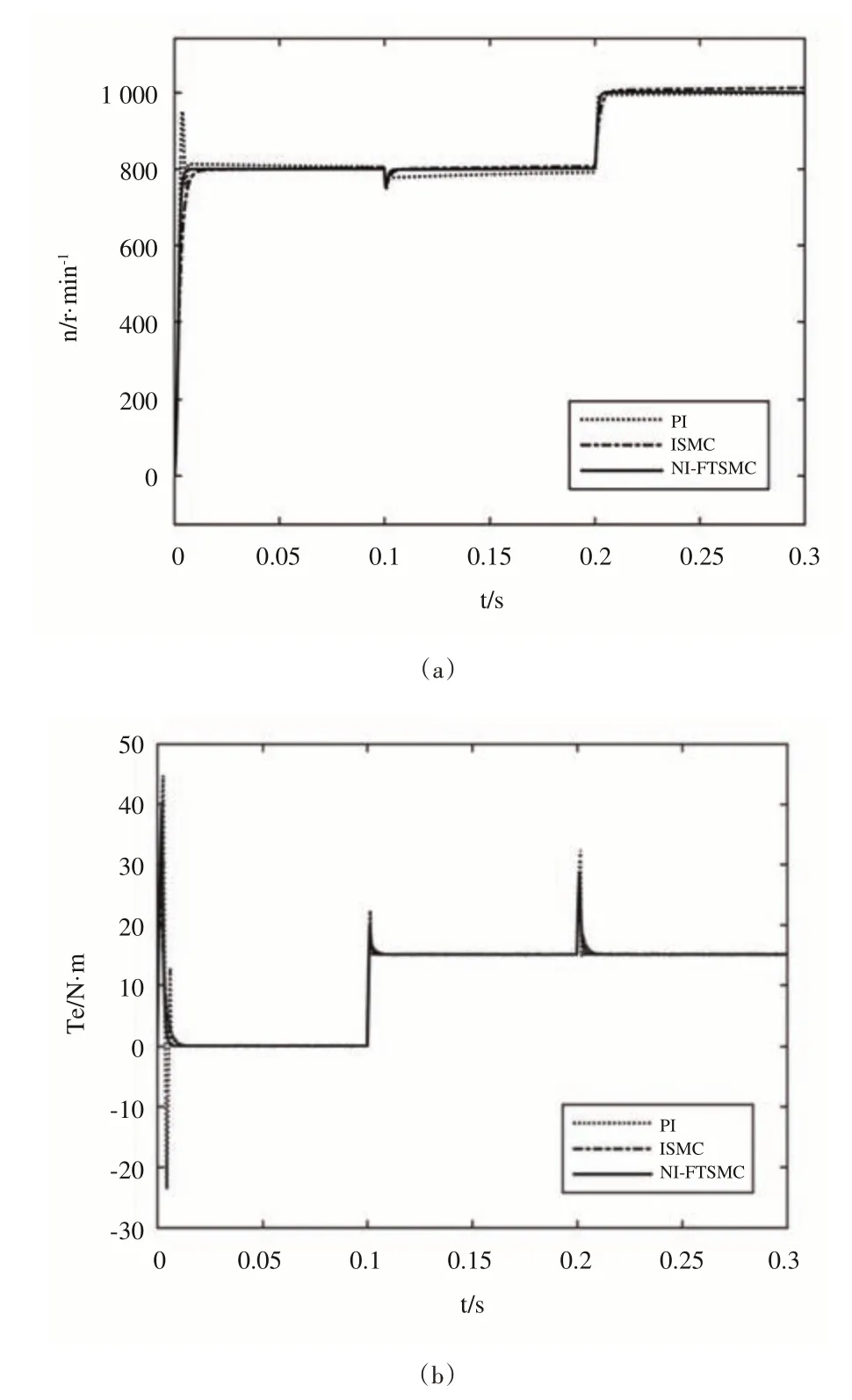
式中,c>0,p、q、m、n均為正奇數且0 如式(1)所示,滑模面由快速終端滑模和積分項兩個部分組成。當s=0 且系統未到達平衡點時,快速終端滑模部分起主要作用,使e快速收斂;當系統接近平衡點時積分項部分起消除穩態誤差作用。其中,G(e)是一類有界非線性光滑函數,可對積分起到減小系統穩態誤差的作用。為了對G(e)進行分析,首先引入以下函數: 其中,g(e)是一類中間高兩邊低的連續函數,對G(e)積分具有放大小誤差的作用,在大誤差處鎖定被積函數G(e)值的優點,可有效避免傳統積分滑模Windup 效應。G(e)的計算公式如式(3): 當δ=γ=2時,G(e)、g(e)的函數圖像如圖1所示。 由圖1 可見,當誤差較小(即|e| ≤δ)時當誤差較大(即|e| ≥δ)時飽和于±γ。通過調整δ和γ值,可實現所需要求的系統控制性能。 Fig.1 Nonlinear function and its derivative圖1 非線性函數及其導數 由于積分項消除穩態誤差存在一定滯后性,因此加入模糊量實現超前微調,通過模糊控制規則實時調整F值。 以表面式PMSM 為被控對象,在建立數學模型時做如下簡化處理:①假設永磁體無阻尼,且氣隙空間磁場正弦分布;②忽略鐵心磁鏈飽和,不計渦流與磁滯損耗;③假設磁路線性,電感參數恒定。 因此,在d-q坐標系下PMSM 電壓方程如下: PMSM 轉矩方程為: PMSM 運動方程為: 其中,ud、uq為d、q軸電壓,id、iq為d、q軸電流,Ld、Lq為d、q軸電感,R為定子電阻,np為電機極對數,wm為轉子機械角速度,ψf為永磁體磁鏈,Te為電磁轉矩,J為轉動慣量,B為摩擦系數,TL為負載轉矩,Ld=Lq。 設定系統狀態變量為: 根據式(6)-式(8)進行求導,可得: 新型積分快速終端滑模面設計如下: 對式(10)進行求導得: 取趨近律為: 聯立式(9)、式(11)和式(12)可得出PMSM 滑模速度控制器為: 接下來,進行系統穩定性分析,定義Lyapunov 方程為: 求導得: 根據Lyapunov 穩定性原理可知,該設計的滑模控制器能在任何初始情況下到達滑模面。 在積分項中加入模糊量實現超前微調,從而抑制由于積分作用引起的滯后效應。建立條件如下: (1)當x1與x2處于論域相反位置(包含中間位置Z0)時,此時的收斂處于正常狀態,設F為Z0以減少干擾。 (2)當x1、x2均為正時,設F為正值;當x1、x2均為負時,設F為負值,控制x1的發散狀態。 (3)當x1為正x2為負時,若x1絕對值較大,設F為正值,加快x1收斂;若x2絕對值較大,設F為負值防止過沖。 (4)當x1為負x2為正時,若x1絕對值較大,設F為負值,加快x1收斂;若x2絕對值較大,設F為正值防止過沖。 在滑移模態控制中,選取系統狀態變量x1和x2為輸入變量,F為輸出變量,使用模糊推理法對輸入、輸出變量進行歸一模糊化處理,記為其中,輸入變量隸屬度函數為Gusussmf類型,論域分別為[-3,3]、[-25,25];輸出變量隸屬度函數為Trapmf 類型,論域為[-18,18]。模糊控制規則設計如表1所示。 Table 1 Fuzzy control rules表1 模糊控制規則表 使用重心法對F進行解模糊計算,通過模糊規則建立的輸入、輸出3D 效果如圖2所示。 Fig.2 3D renderings of fuzzy control system圖2 模糊控制系統3D效果圖 為驗證本文所提出的控制策略的合理性及優越性,在MATLAB/Simulink 環境下搭建PMSM 調速系統仿真模型,采用id=0 的雙閉環矢量控制方式。在轉速環中將運用3種不同的控制器,分別為PI、傳統積分型滑模控制器(ISMC)和新型積分快速終端滑模控制器(NI-FTSMC),電流環采用傳統PI 控制器。系統結構框圖如圖3 所示。PMSM 參數如表2所示。 Fig.3 System structure framework圖3 系統結構框架 Table 2 Parameters of PMSM表2 永磁同步電機參數 仿真實驗的具體參數配置如下:仿真時間為0.3s,在轉速800r · min-1下空載啟動,運行0.1s 后突然增加15N ·m的負載,再過0.1s后將轉速提升至1 000r · min-1。 空載啟動后,3 種不同控制器控制下的系統動態響應結果如圖4所示。 Fig.4 Dynamic response of the system at no-load startup圖4 空載啟動系統動態響應 由圖4 可見,在空載啟動階段,PI 控制下的轉速波形出現了嚴重的超調及波動;ISMC 控制下的轉速調節時間較長,同時出現了轉速誤差;本文提出的NI-FTSMC 轉速調節時間最短,且未產生超調和波動。 突加負載后,3 種不同控制器控制下的系統響應如圖5所示。 Fig.5 System dynamic response when a sudden load is applied圖5 突加負載下系統動態響應 由圖5 可見,在突加負載的情況下,PI 控制下的轉速無法迅速恢復到給定狀態;ISMC 控制下的轉速響應速度較慢,且誤差依舊存在;而在NI-FTSMC 控制下的轉速波形響應迅速,波動小,無超調,轉速跟蹤精準。 轉速突變后,3 種不同控制器控制下的系統響應如圖6所示。 Fig.6 Dynamic response of the system with a given speed change圖6 給定轉速突變系統動態響應 由圖6 可見,當給定轉速突變后,ISMC 發生了由積分作用累積造成的誤差增大的結果,這意味著控制系統需要更長的時間消除誤差;NI-FTSMC 顯現出了在各種干擾情況下優越的控制性能。 3 種不同控制器控制下的系統總體運行結果如圖7所示。 Fig.7 Overall operating results of the system圖7 系統總體運行結果 由圖7 可見,PI 控制下的轉速和電磁轉矩波形波動最為明顯,同時轉速難以穩定跟蹤,效果最差;ISMC 在經歷頻繁干擾后,在積分累積作用下會出現誤差增大的現象,干擾會造成消除誤差的時間增長,系統抗擾性也隨之變弱;NI-FTSMC 反應靈敏,未發生超調現象,而且能夠穩定跟蹤,動靜態性能十分優越。 綜上所述,本文所提出的NI-FTSMC 方法相較于PI 和傳統積分型滑模控制器(ISMC)而言,性能更加優越。 本文通過結合積分型滑模控制的概念,基于快速終端滑模控制方法,在滑模面中引入改進積分項,在保留快速終端滑模控制優點的同時,相較于傳統滑模面具有更快的收斂速度。 此外,將積分項設計為非線性函數加模糊量的形式,能夠在有效消除穩態誤差的同時,盡可能的避免積分Windup 效應,顯著提高了系統的控制性能。 針對PMSM 矢量控制調速系統的特點,通過設計新型積分快速終端滑模速度控制器,并與傳統PI 和積分型滑模控制器進行比較。實驗結果表明,所設計的滑模控制器能夠有效提高系統的調速性能,為改善PMSM 調速系統的動態品質提供了一種有效的方法,但該控制方式需要設定較多參數,仍然還有較大的改進空間。

2 新型積分快速終端滑模控制器設計
2.1 PMSM 數學模型
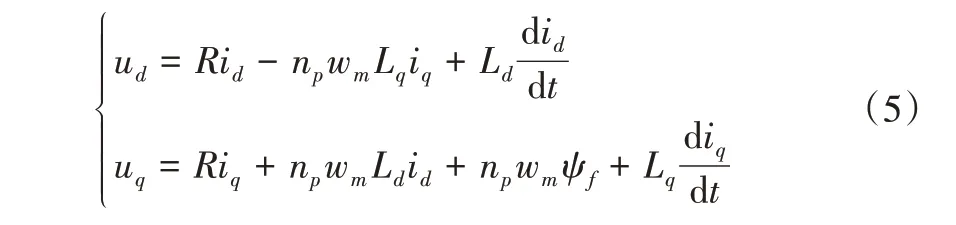

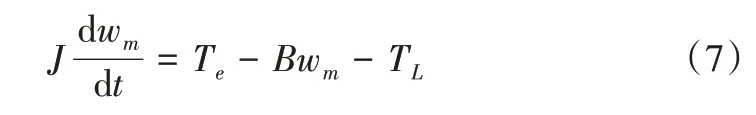
2.2 PMSM 滑模速度控制器

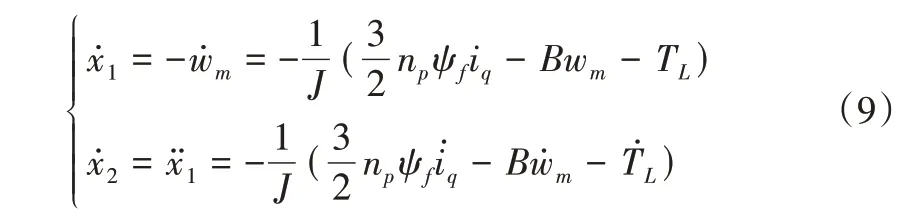
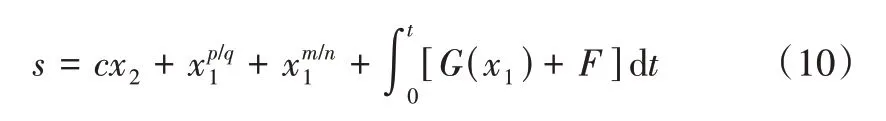
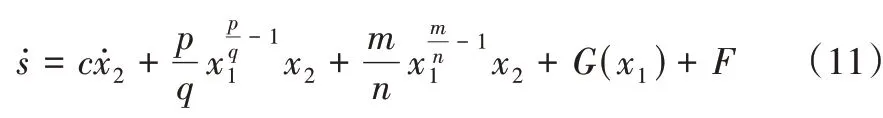
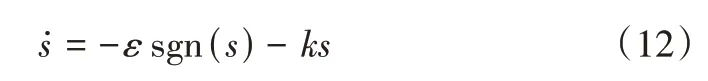
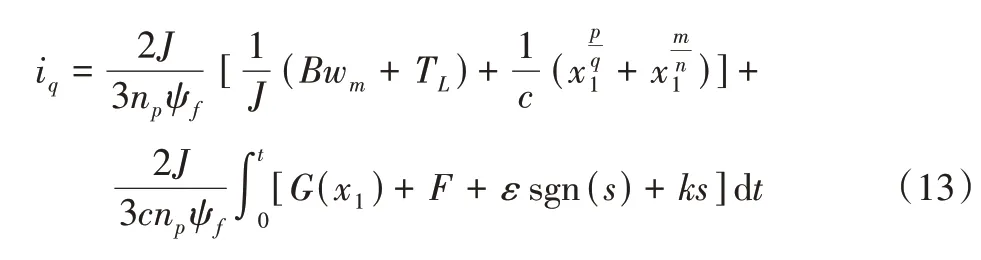

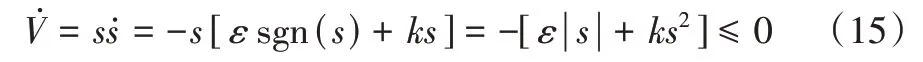
2.3 模糊控制器設計


3 仿真實驗
4 結語

