不同曲線半徑下彎橋抗傾覆穩定性分析

束文陽，紀海龍

(1.安徽省交通規劃設計研究總院股份有限公司，安徽 合肥 230088；2.公路交通節能環保技術交通運輸行業研發中心，安徽 合肥 230088)

1 抗傾覆機理

周所周知，單支座無法對梁體扭轉變形產生約束，同一個橋墩的多支座可以對扭轉變形的扭矩起到雙重約束。正常情況下，對于不同曲線半徑下的箱型梁橋各支座均應處于受壓狀態。然而，當上部荷載超限或偏載嚴重時，將產生較大的傾覆力矩，此時偏載另一側的支座會逐步脫空，直到只剩一個有效支座時，便失去對箱梁的抗扭約束，當所有橋墩支承均失去對扭轉變形的約束的時候，此時傾覆達到臨界狀態。隨著扭轉變形的進一步發展，梁體將發生傾倒、垮塌，連帶支座和下部結構損毀。

有關橋梁抗傾覆穩定性的計算方法一直以來便存有爭議，老版《公路鋼筋混凝土及預應力混凝土橋涵設計規范》(JTG D62—2004)中由于沒有關于橋梁抗傾覆穩定的相關計算要求，因而目前在運營的公路橋梁當中，大多沒有考慮過橋梁傾覆問題。隨著社會的不斷發展，荷載等級的進一步提升，橋梁傾覆問題便開始大量涌出，橋梁抗傾覆穩定也得到了進一步的重視，《公路鋼筋混凝土及預應力混凝土橋涵設計規范》(JTG D62—2012征求意見稿)(以下簡稱混規2012征求意見稿)首次給出了公路橋梁抗傾覆驗算的計算方法及公式[4]，但仍有爭議。混規2012征求意見稿中針對中小跨徑橋梁提出采用整體式斷面來驗算橋梁上部結構的抗傾覆穩定性，橋梁抗傾覆穩定性應滿足公式(1)要求

(1)

式中：γqf為抗傾覆穩定系數；Ssk為標準組合下使橋梁發生傾覆的汽車荷載(含沖擊作用)產生效應(效應)；Sbk為標準組合下抵抗橋梁上部結構傾覆的作用效應(抗力)。

混規2012征求意見稿中關于橋梁抗傾覆計算的類型共包含兩種，一種是正交橋梁和斜交角小于30°的斜交橋梁，另一種則是曲線橋。對于曲線橋，當中墩支承均位于橋臺或分聯墩曲線外側支承連線的內側時，傾覆軸線即為橋臺曲線外側支承連線；當跨中橋墩支承均位于橋臺曲線外側支承連線外側時，傾覆軸線即是某個橋臺或分聯墩曲線外側支承和中墩支承的連線。上部結構抗傾覆穩定性系數計算采用公式(2)

(2)

式中：qk為車道荷載中均布荷載；Pk為車道荷載中集中荷載；u為沖擊系數；RGi為恒載各支座的支反力；xi為各個支座到傾覆軸線的垂直距離；e為移動活載車道線與傾覆軸線所圍成的陰影部分面積；Ω為移動活載車道線與傾覆軸線最大垂直距離。

參考《公路鋼筋混凝土及預應力混凝土橋涵設計規范》(JTG 3362—2018)(以下簡稱混規2018)規定，橋梁的抗傾覆穩定性驗算采用“抵抗力矩≥抗傾覆穩定性系數×效應力矩”的型式。按各作用的標準組合計算時，橋梁抗傾覆穩定性應符合以下要求

(3)

式中：∑Sbk,i為使上部結構穩定的效應設計值；∑Ssk,i為使上部結構失穩的效應設計值；li為脫空支座與有效受壓支座的支座的距離；RGki為恒載標準組合作用下，按全部支座受壓的支承體系來計算確定的第i個橋墩處脫空支座的支座反力；RQki為可變荷載標準組合作用下，按全部支座受壓的支承體系計算確定的第i個橋墩處脫空支座的支座反力，考慮沖擊系數的汽車荷載按各脫空支座對應的最不利布置型式取值[5]。

混規2012征求意見稿中將梁體視為剛體，以車道荷載來計算傾覆力矩，以成橋狀態下恒載支反力來計算抗傾覆力矩。橋梁在傾覆過程中梁體的結構變形是剛體和扭轉運動的結合，顯然混規2012征求意見稿中的計算方法是一種簡化處理，其次，箱梁按照傾覆軸線切割后各力矩的求解也變得復雜。混規2018將扭轉因素考慮進來后，通過支座抗扭抵抗矩與傾覆力矩的比較來計算抗傾覆穩定性，這更為合理，計算也變得簡單。但是，各力矩中的力臂為脫空支座與受壓支座之間的距離，是個定值，且條文說明中認為箱梁橋處于傾覆臨界特征狀態時，每個橋墩都存在一個受壓支座，即相當于傾覆軸線為各有效支座的連線，與橋梁軸線曲率并沒有關系。綜上，橋梁傾覆是一個相當復雜的過程，國內外對于抗傾覆的驗算方法和要求也不盡相同，現依據混規2018來進行有限元建模計算分析。

2 建模計算

2.1 結構尺寸

以互通立交匝道橋中最為常見的4×20 m一聯單箱單室普通鋼筋混凝土現澆箱型梁橋為例，現澆箱梁頂板寬度為850 cm，底板寬度為450 m，懸臂長度為200 cm，梁高為150 cm。

2.2 支座布置

考慮匝道橋在被交路中分帶落墩或其他常見橋下空間限制因素等情況，中墩采用一個或多個獨柱墩，即單支座，兩側其余墩臺采用雙支座，支座中心距350 cm，典型支座布置示意如圖1所示，圖中數字為支座編號。

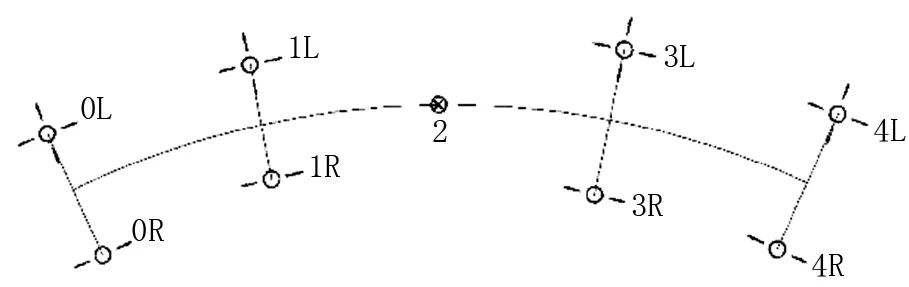
圖1 支座布置示意圖

2.3 模型建立

采用橋梁博士V4.4.1有限元軟件進行建模計算，選用最新的2018公路規范，定義運營階段抗傾覆穩定性分析。按左、右各橫向偏移2.35 m進行縱向移動荷載的加載，分別計算左傾(曲線外側)和右傾(曲線內側)抗傾覆穩定系數。計算模型如圖2所示。

圖2 抗傾覆驗算模型

3 穩定性分析

3.1 計算結果

根據主梁軸線曲線半徑及獨柱墩數量的不同，共分六個計算工況。

表1 計算工況一覽表

在擬定的驗算條件下橋梁上部結構抗傾覆穩定系數的計算結果匯總如下。

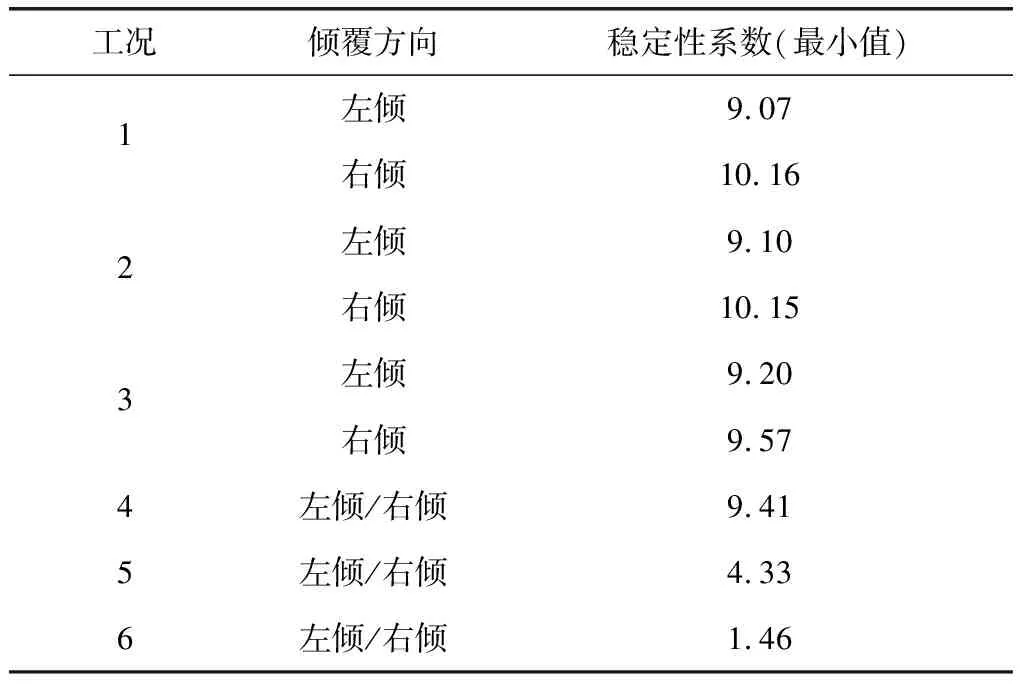
表2 抗傾覆穩定性系數

3.2 統計分析

(1)一個獨柱墩情況下，曲線半徑對抗傾覆穩定系數的影響

控制獨柱墩數量不變，均按2#墩采用單支座，其余墩臺采用雙支座，即對工況1至工況4的計算結果進行統計分析，箱梁外傾和內傾的抗傾覆穩定系數隨彎橋曲線半徑變化分別如圖3和圖4所示。

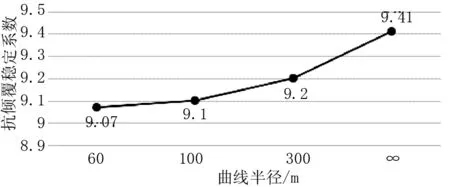
圖3 抗傾覆穩定系數(外傾)

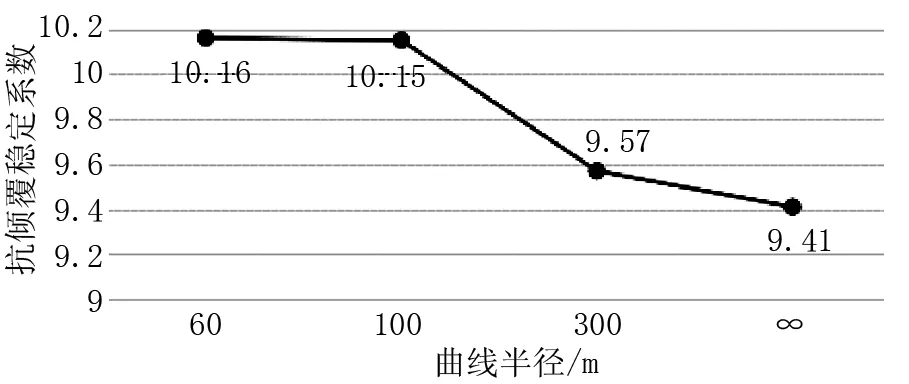
圖4 抗傾覆穩定系數(內傾)

由圖可得出。

①在不同的曲線半徑下箱梁內傾的抗傾覆穩定系數始終大于外傾，即對于彎橋而言，箱梁的橫向傾覆更容易發生在曲線外側。

②外傾的抗傾覆穩定系數隨曲線半徑的增大而提高，而內傾的抗傾覆穩定系數隨半徑的增大而降低。結合(1)即曲線半徑越大箱梁抗傾覆穩定系數的最小值是增大的。這相較于常規理解相悖，究其主要原因，是計算方法不同[6]。新規范中采用的穩定效應與失穩效應的計算力臂為失效支座與有效支座的支座中心距，而不是支座到傾覆軸的距離。

③按新規范的計算方法，不同曲線半徑下彎橋內、外側抗傾覆穩定系數有一定變化，但差值并不大，曲線半徑對抗傾覆穩定性并不敏感。

④對于一聯僅采用一個獨柱墩的彎橋來說，在不同的曲線半徑下，在設定計算條件下，抗傾覆穩定系數始終大于2.5，滿足混規2018抗傾覆穩定性要求。

(2)曲線半徑相同的情況下，獨柱墩數量對抗傾覆穩定系數的影響

控制曲線半徑相同，獨柱墩數量不同，即對工況4至工況6的計算結果進行統計分析，箱梁抗傾覆穩定系數隨獨柱墩數量變化圖如下。

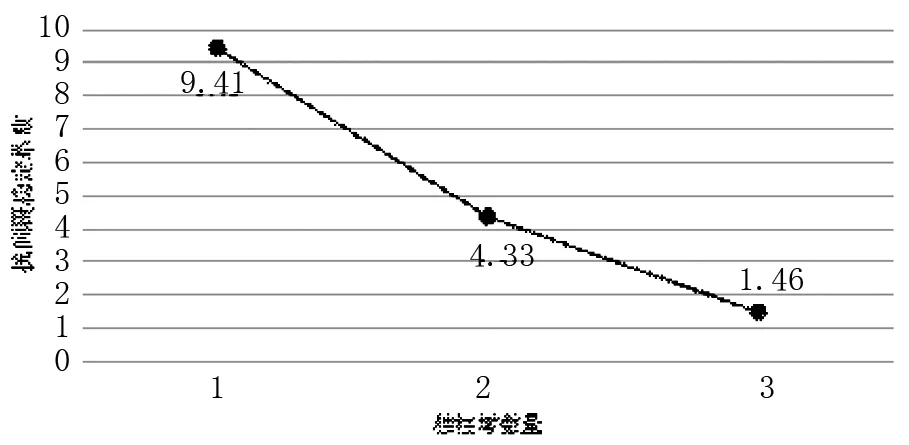
圖5 抗傾覆穩定系數

由上圖可得出：抗傾覆穩定系數隨獨柱墩數量的增加而有較大幅度的下降，當一聯含有2個獨柱墩時，抗傾覆穩定性已經沒有太多的富余，當一聯含有3個獨柱墩時，抗傾覆穩定性不滿足規范要求。這一結果也驗證了交通運輸部2021年2月發布的《公路危舊橋梁排查和改造技術要求》中的有關規定。《公路危舊橋梁排查和改造技術要求》規定：同一聯中連續3個及以上橋墩均為獨柱墩時，該聯不再進行結構驗算，應進行改造提升，少于3個獨柱墩的情況應進行抗傾覆穩定性驗算。

4 結 論

(1)彎橋曲線外側抗傾覆穩定系數小于內側，對于單車道的匝道橋，若考慮右側硬路肩不行車，左轉匝道相對而言對抗傾覆更有利，但若橋梁較寬或考慮特殊情況下硬路肩行車，右轉匝道相對而言對抗傾覆更有利。即對于彎橋靠曲線內側行車更不容易發生傾覆。

(2)按新規范計算出的抗傾覆穩定系數對曲線半徑并不敏感，曲線半徑越小，抗傾覆穩定系數越小。

(3)一聯存在連續3個及以上獨柱墩的橋梁具有極大的傾覆風險，在設計過程中應該嚴格禁止，既有橋梁應及時加固；對于一聯存在連續2個獨柱墩的情況應當加強驗算，設計宜避免，既有橋梁宜及時加固。

(4)對于一聯僅設置一個獨柱墩的彎橋來說，抗傾覆穩定性一般情況下能夠滿足規范要求，在設計中可以結合抗傾覆驗算結果靈活使用，沒有必要為了避免獨柱墩而強行使用多支座或大跨徑。