基于新型卸荷槽的齒輪泵內(nèi)部流場及空化特性分析*

李镕熙,周 龍,周振華,萬 方,張國慶*

(1.北京理工大學 宇航學院,北京 100081;2.中國航發(fā)貴州紅林航空動力控制科技有限公司 產(chǎn)品設計所,貴州 貴陽 550009)

0 引 言

航空燃油泵是飛機發(fā)動機的關鍵組成部分,是常見的液壓正排量裝置,其主要作用是輸送航空燃油,其性能的優(yōu)劣對航空發(fā)動機的運行有重要影響。

航空燃油泵的主要類型有齒輪泵、離心泵、柱塞泵等多種結構形式,而齒輪泵有體積小、效率高、結構簡單的特點。相比于普通齒輪泵,航空燃油泵具有轉速高、流量大、易發(fā)生空化現(xiàn)象等特點[1-6]。

有關于齒輪泵內(nèi)流特性和空化方面的研究一般有3種方法:(1)數(shù)學解析法,(2)實驗分析法,(3)數(shù)值模擬法。因為齒輪泵內(nèi)流屬于復雜的三維非定常流動,理論分析和實驗研究周期長、難度大,故主流的研究方法是利用數(shù)值模擬法研究齒輪泵流動和空化特性[7-10]。

目前,針對齒輪泵內(nèi)部流場出現(xiàn)的空化現(xiàn)象進行的研究已有不少。江傳惠等人[11]根據(jù)實驗數(shù)據(jù),對齒輪泵內(nèi)部流場空化初生的原因做出了推斷,但是該方法缺少在工程實例中的應用。李晗[12]研究了極限轉速下齒輪泵的空化現(xiàn)象,分析了影響齒輪泵流場的各種因素,但是缺少轉速對空化現(xiàn)象的影響方面的研究。劉兆領等人[13]研究了特定工況下齒輪泵卸荷槽的設計,并對齒輪泵流場進行了分析,但是缺少工程試驗來對該設計效果進行分析驗證。王安麟[14]研究了齒輪泵的吸油腔空化現(xiàn)象,并給出了相應的改進方案,發(fā)現(xiàn)了該方案不僅可以降低齒輪泵的整體流量,同時也能夠提高齒輪泵流場內(nèi)的流動穩(wěn)定性;但是該研究也同樣缺少試驗來對此進行驗證。

目前,國內(nèi)外研究人員對航空燃油齒輪泵內(nèi)流場空化受轉速的影響規(guī)律研究較少。因此,筆者設計一種能降低空化影響的新型卸荷槽,并對泵內(nèi)流場的流動特性進行研究。

首先,筆者對一種新型卸荷槽齒輪泵性能進行分析,然后,在不同轉速工況下,針對航空燃油齒輪泵內(nèi)流特性和空化現(xiàn)象,進行基于Pumplinx軟件的數(shù)值模擬研究,最后,進行試驗驗證,以期對今后航空燃油泵的相關設計提供參考。

1 齒輪泵模型

1.1 幾何模型

筆者所研究的對象為航空燃油齒輪泵。考慮到齒輪泵倒角等結構對其流場的影響較小,故在實際流場的基礎上,筆者對齒輪泵流場模型進行相應的簡化。

筆者所采用的流場幾何模型由吸油腔、壓油腔、齒輪和卸荷槽組成。

齒輪泵流場幾何模型如圖1所示。

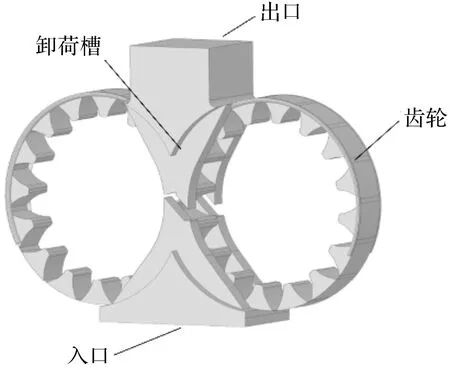
圖1 齒輪泵流場幾何模型

航空燃油齒輪泵參數(shù)如表1所示。

表1 航空燃油泵齒輪參數(shù)

筆者設計的新型卸荷槽的幾何模型如圖2所示。

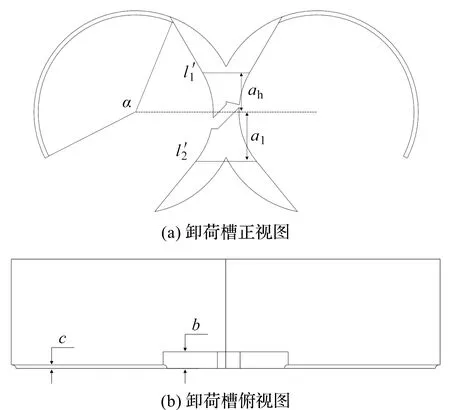
圖2 新型卸荷槽幾何模型

航空燃油齒輪泵的卸荷槽參數(shù)如表2所示。

表2 卸荷槽參數(shù)

1.2 網(wǎng)格與邊界條件

齒輪泵內(nèi)部流場屬于三維非定常流動,如果利用一般動網(wǎng)格技術,因為齒輪狹縫狹窄,會導致時間步長太短,計算成本過高。而Pumplinx軟件利用二叉樹法在出入口及卸荷槽生成笛卡爾網(wǎng)格,通過內(nèi)置網(wǎng)格生成模塊,在齒輪處生成結構網(wǎng)格,可以有效提高計算效率。

在對模型進行前處理時,筆者將嚙合輪齒之間的縫隙調(diào)至0.05 mm,齒頂和泵體之間的縫隙調(diào)至0.04 mm。

齒輪泵網(wǎng)格圖如圖3所示。

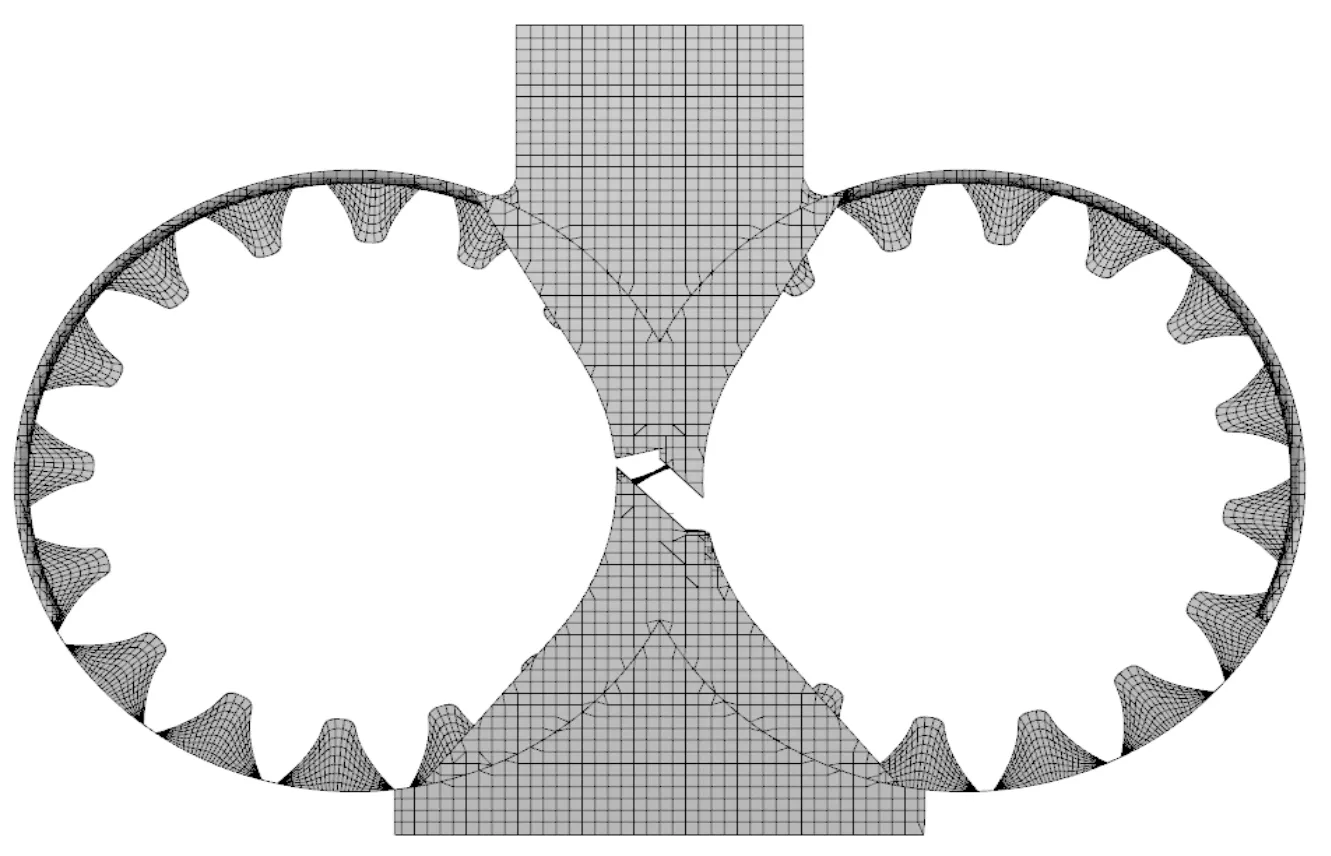
圖3 齒輪泵網(wǎng)格圖

齒輪泵內(nèi)流場的邊界條件設置如下:

齒輪泵入口邊界條件為壓力入口,壓力值為0.345 MPa;出口邊界條件為壓力出口,壓力值為8 MPa;溫度為300 K;齒輪設置為external gear模型;其他壁面設置為靜止無滑移壁面;各計算域交界面設置為mismatched grid interface;

流體區(qū)域材料為航空煤油,相關物理參數(shù):密度為800 kg·m-3,動力黏度為7×10-3kg·m-1·s-1,氣體質(zhì)量分數(shù)為9e-5。

在利用PumpLinx對齒輪泵內(nèi)部流場進行動態(tài)數(shù)值計算時,在齒輪泵的轉速n=6 000 r·min-1的情況下,齒輪泵旋轉周期為T=0.01 s。

為使得到的數(shù)據(jù)相對準確和穩(wěn)定,該處模擬齒輪泵的轉數(shù)為4轉,取后2轉的結果進行分析,齒輪每轉0.75°時,數(shù)值計算結果保存一次。

在無卸荷槽和矩形卸荷槽的齒輪泵數(shù)值計算中,以及齒輪泵在4種轉速n=5 500 r·min-1,n=6 000 r·min-1,n=6 500 r·min-1,n=7 000 r·min-1的數(shù)值模擬中,所有設置均與上述相同。

2 數(shù)值模擬基礎與空化模型

2.1 數(shù)值模擬基礎

齒輪泵內(nèi)部流動為非定常不可壓縮黏性流動,需要滿足質(zhì)量守恒、動量守恒和能量守恒方程。此處的湍流模型選擇標準k-ε模型[15-19]。具體如下:

(1)質(zhì)量守恒(方程)。

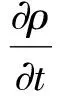
(1)

式中:ρ—流體密度;—哈密頓算子;u—速度矢量。

對于齒輪泵中的不可壓縮流體,可化簡為:

ρ(·u)=0

(2)

(2)動量守恒方程。

齒輪泵流場滿足基于牛頓第二定律的動量方程,即流體控制微元動量的變化率等于該微元體積上質(zhì)量力和面力之和,其表達式為:

(3)

式中:u,ν,w—x,y,z方向速度分量;μ—動力黏性系數(shù);u—速度矢量;gradu,gradν,gradw—x,y,z方向速度梯度;Su,Sν,Sw—廣義動量守恒源項。

(3)能量守恒方程。

齒輪泵流場滿足能量守恒定律,即控制微元中能量的增量等于該控制微元吸收的凈熱量與外力對其做功之和,其表達式為:

(4)

式中:T—流體溫度;k—導熱系數(shù);cp—定壓比熱容;ST—流體能量和流體黏性產(chǎn)生的傳遞能量。

(4)湍流模型。

在Pumplinx數(shù)值模擬中,采用標準k-ε湍流模型進行求解,其輸運方程為:

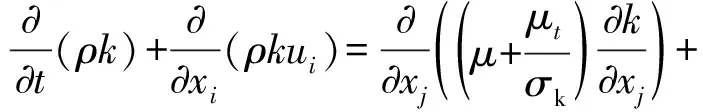
Gk+Gb+ρε-Ym+Sk

(5)

(5)

式中:μ—動力黏度;μt—湍動黏度;σk,σε—湍動能和耗散率對應的普朗數(shù);Gk—平均速度梯度引起的湍動能產(chǎn)生項;Gb—浮力湍動能;Ym—總耗散率;C1ε,C2ε,C3ε—經(jīng)驗常數(shù);Sk,Sε—自定義條件。

2.2 空化模型

基于Pumplinx進行數(shù)值模擬時,筆者所采用的是全空化模型[20-22]。基于兩相流理論,筆者利用Rayleigh-plesset方程描述氣泡的析出和溶入,同時利用混合密度概念,其表達式如下:

(7)

式中:ρm—平均密度;ρ1—流體密度;ui—平均速度;fv—氣相質(zhì)量分數(shù);Γ—有效傳遞系數(shù);pv—氣象臨界壓力;Ce,Cv—經(jīng)驗常數(shù);K—湍流動能。

3 計算結果分析

3.1 新型卸荷槽性能提升

在轉速保持6 000 r/min的工況下,筆者對無卸荷槽齒輪泵、矩形卸荷槽齒輪泵和新型卸荷槽齒輪泵進行數(shù)值計算,得到相關物理量的分布。

在齒輪的嚙合過程中,嚴重的困油會對齒輪泵出口流量以及流場品質(zhì)造成影響,而新型卸荷槽能降低該不良影響。

筆者取3種齒輪泵的0.02 s～0.04 s的仿真數(shù)據(jù)進行后處理分析,利用質(zhì)量流量和脈動系數(shù)來比較各齒輪泵的流量品質(zhì)。

各類型卸荷槽特征質(zhì)量流量與脈動系數(shù)如表3所示。

表3 特征質(zhì)量流量與脈動系數(shù)

由表3可知:與無卸荷槽齒輪泵相比,新型卸荷槽齒輪泵的平均流量下降2.99%,脈動系數(shù)降低40.32%;與矩形卸荷槽齒輪泵相比,新型卸荷槽齒輪泵的平均流量下降6.89%,脈動系數(shù)降低44.61%。

筆者所研究的3種齒輪均為16齒非標準齒輪,因此,在正常工作過程中,對比3種齒輪泵其內(nèi)部流場的空化情況時,只需要分析一對相互配合的輪齒在轉過相同角度過程中泵內(nèi)的空化情況即可,并取泵第3轉初始位置的空化云圖進行對比分析。

3種齒輪泵內(nèi)部流場的總體氣體體積分數(shù)FT分布情況,如圖4所示。

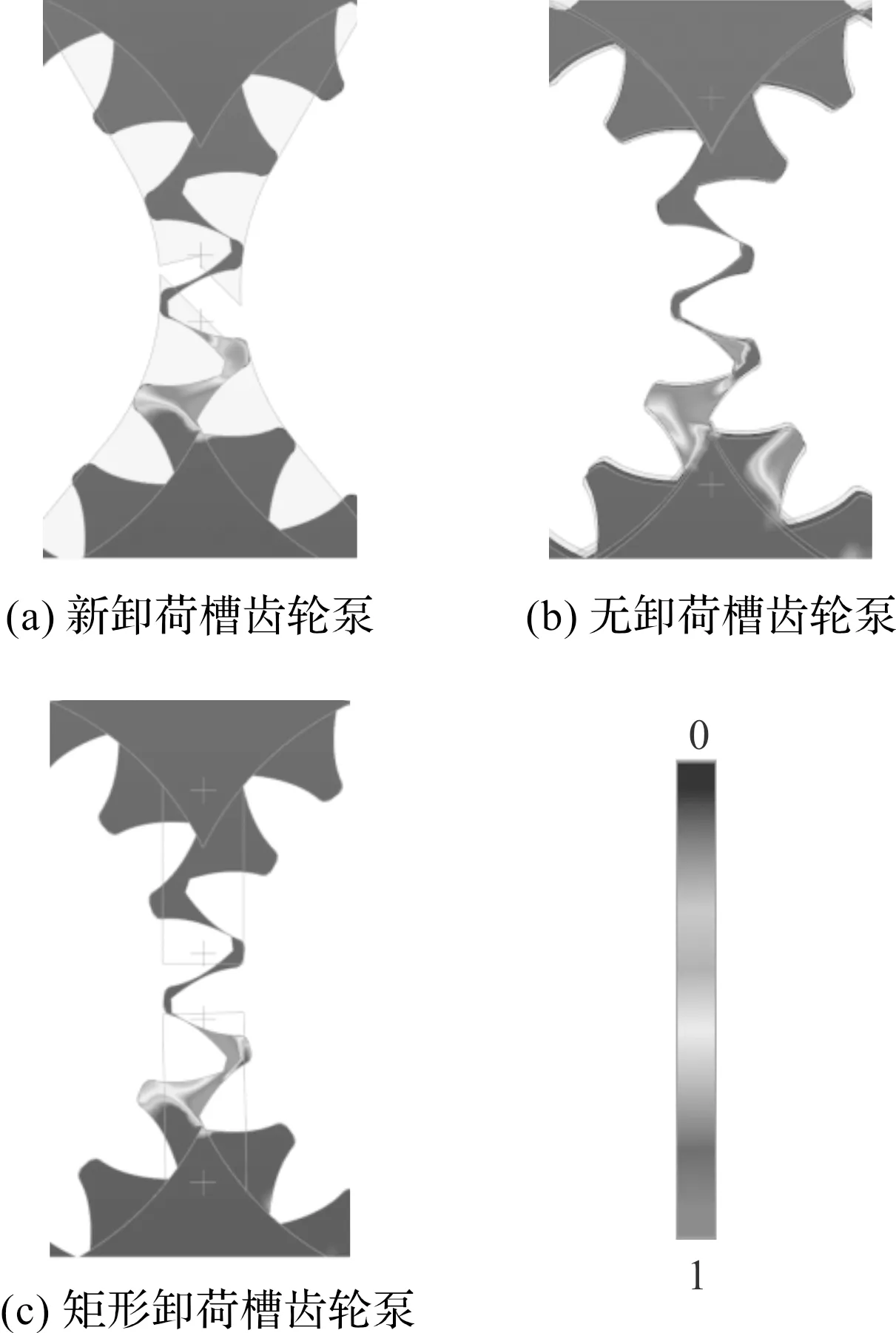
圖4 總體氣體體積分數(shù)FT分布情況

由圖4可知:泵的總體氣體體積分布主要集中在吸油區(qū)和嚙合區(qū),新卸荷槽齒輪泵空化范圍和強度最小,而無卸荷槽齒輪泵空化現(xiàn)象最為明顯;矩形齒輪泵質(zhì)量流量最大,無卸荷槽的齒輪泵脈動系數(shù)最高,新卸荷槽齒輪泵在質(zhì)量流量損失在7%以內(nèi)的情況下,減少了流量脈動的44%,有效提高了齒輪泵流場質(zhì)量。

以上結果證明了新型卸荷槽在降低空化現(xiàn)象方面的高效性,與降低出油口流量脈動方面的有效性,為漸開線外嚙合齒輪泵卸荷槽的創(chuàng)新設計提供了一種新的途徑。

3.2 轉速對齒輪泵流場影響

為實現(xiàn)齒輪泵大流量供油,最有效的途徑就是提高齒輪的轉速,但高轉速易使齒輪泵的空化現(xiàn)象加劇。

筆者對齒輪泵不同轉速n=5 500 r·min-1,n=6 000 r·min-1,n=6 500 r·min-1,n=7 000 r·min-1分別進行數(shù)值計算,分析齒輪泵內(nèi)部油液流動規(guī)律,研究轉速對空化特性的影響。

筆者在泵內(nèi)設置4個監(jiān)測點,其中,監(jiān)測點1位于壓油腔,監(jiān)測點2位于吸油腔,監(jiān)測點3位于壓油腔卸荷槽,監(jiān)測點4位于吸油腔卸荷槽。

在不同轉速下,齒輪泵流場壓力的分布如圖5所示。

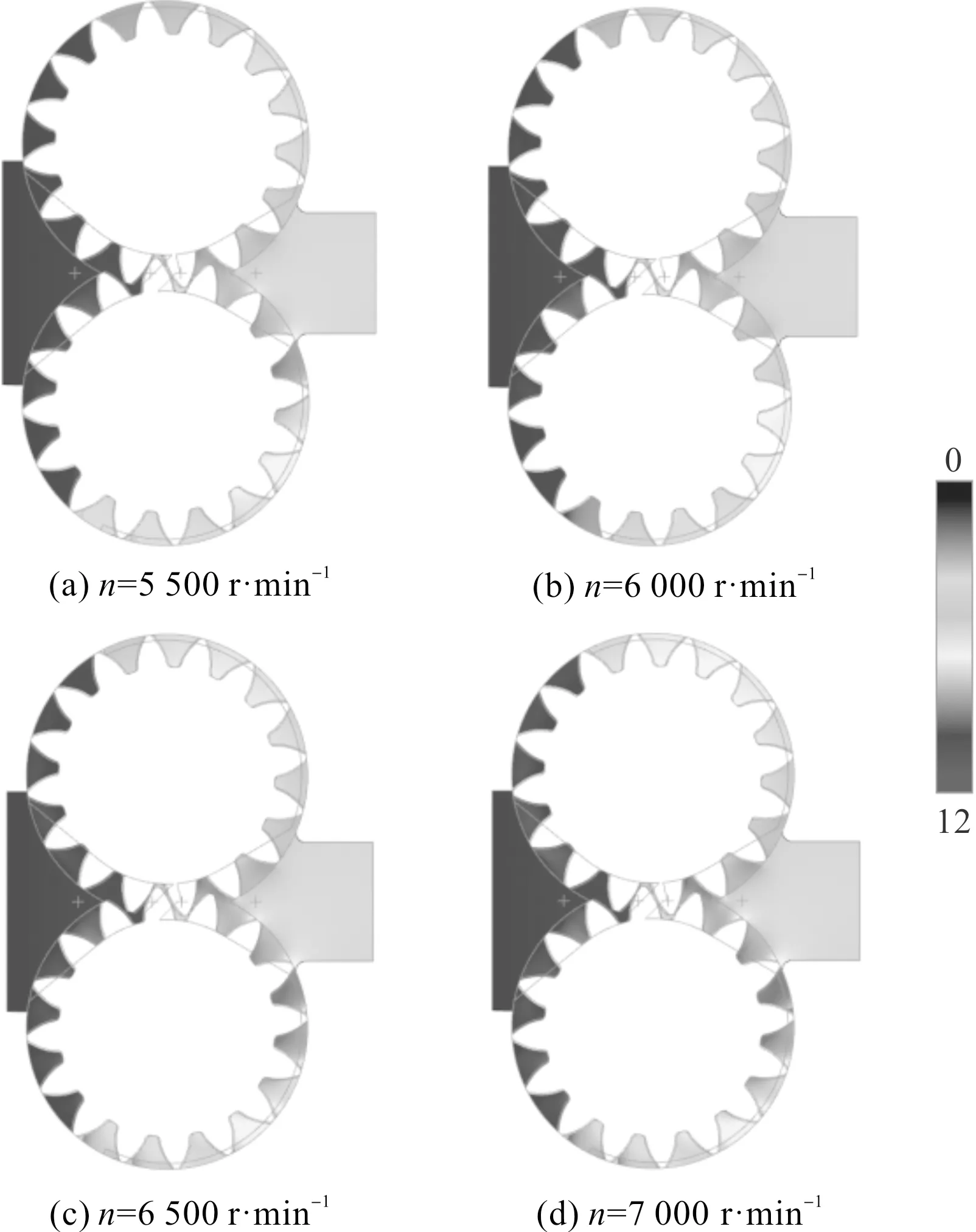
圖5 不同轉速流場壓力分布

由圖5可以看出:在高于5 000 r/min轉速的情況下,當齒輪處于相同位置時,隨著轉速n的逐漸上升,齒輪泵內(nèi)部流場的壓力分布情況變化不大;最大壓力Pmax出現(xiàn)在壓油腔齒輪嚙合處,大于出口壓力;最小壓力Pmin出現(xiàn)在吸油腔齒輪分離處,小于出口壓力。

在不同轉速下,齒輪泵各監(jiān)測點壓力如圖6所示。

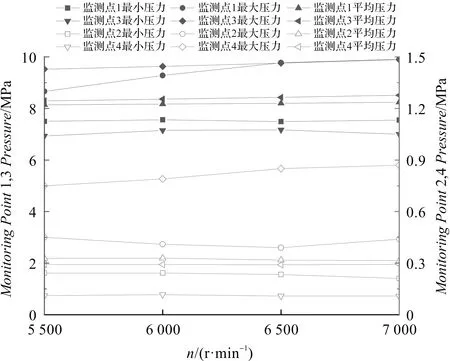
圖6 齒輪泵各監(jiān)測點壓力

由圖6可以看出:在不同轉速下,4個監(jiān)測點的壓力的變化幅度不明顯,4個監(jiān)測點的最大壓力都隨著轉速的增加而增加;壓油腔的監(jiān)測點平均壓力隨著轉速的增加而增加,吸油區(qū)的監(jiān)測點平均壓力隨著轉速的增加而減少。

齒輪泵內(nèi)部的流場流速分布如圖7所示。

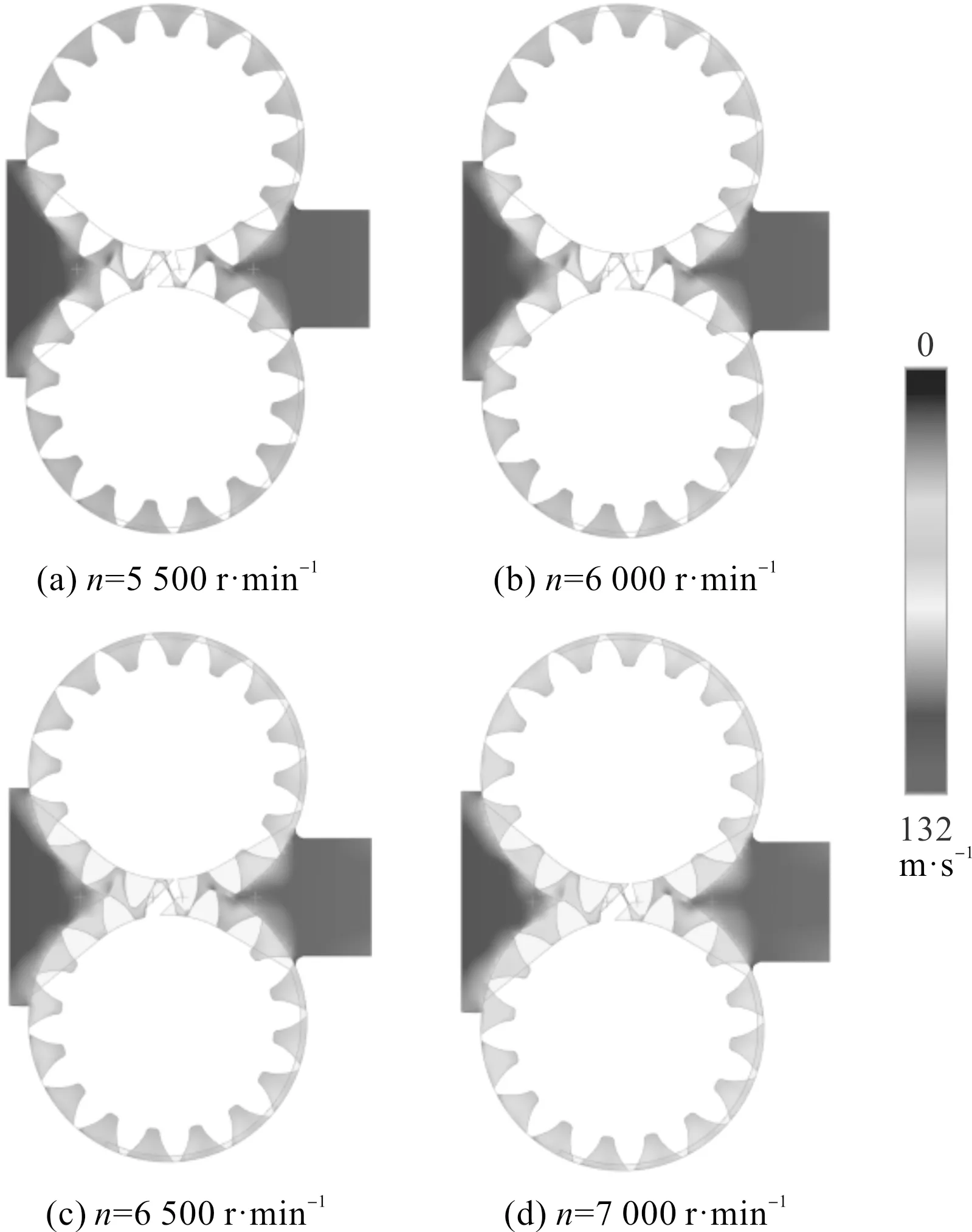
圖7 齒輪泵內(nèi)部流場流速分布

由圖7可知:在不同的轉速下,齒輪泵的流場流速分布相同,最高流速存在于齒輪的嚙合處,其速度遠大于齒輪外側的線速度;在齒輪擠壓的作用下,由于嚙合處封閉空間的體積急劇變化,嚙合處會存在較大的壓差。

在不同的轉速下,最大流速Vmax如表4所示。

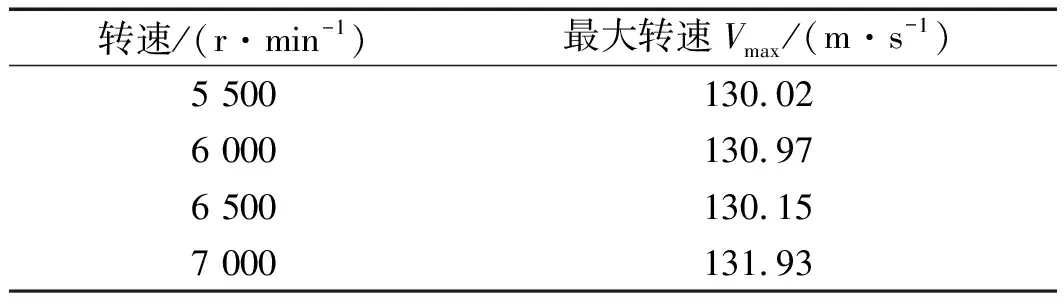
表4 流場最大流速

由表4可知:當齒輪轉速逐漸增大,流場的最大速度逐漸增大,但是變化幅度小,轉速從5 500 r/min提高到7 000 r/min,流場最大速度僅提高1.38%。這一現(xiàn)象說明,當轉速達到一定程度時,流場最大速度增長與齒輪轉速增加并非線性關系。

在4種轉速下,總體氣體體積分數(shù)FT如圖8所示。

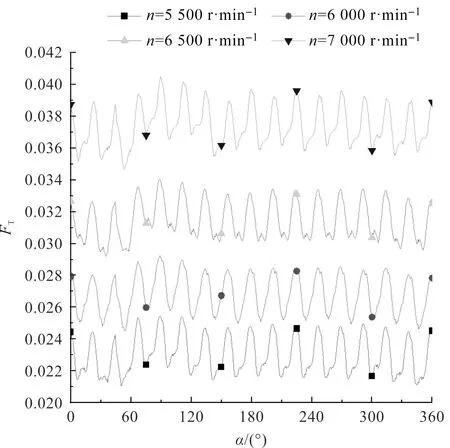
圖8 總體氣體體積分數(shù)FT

由圖8知:在每一對輪齒進入嚙合,到退出嚙合的過程中,齒輪泵內(nèi)流場的氣體體積分數(shù)都要經(jīng)歷一次波動,這表明泵內(nèi)流場的空化程度也會隨之經(jīng)歷一次波動;隨著轉速的逐漸增加,齒輪泵內(nèi)部流場的氣體體積分數(shù)的最大值、最小值都在逐漸增大,因此,隨著轉速的逐漸提高,齒輪泵內(nèi)部流場整體的空化程度在逐漸增大。

齒輪泵內(nèi)部流場的總體氣體體積分數(shù)FT分布情況,如圖9所示。

圖9 總體氣體體積分數(shù)FT分布情況

由圖9可知：隨著齒輪泵轉速的提高,齒輪泵嚙合處FT的數(shù)值和分布范圍都在逐漸增大。

4 對比試驗

為了驗證上述仿真模型的準確性,筆者對新型卸荷槽齒輪泵的質(zhì)量流量進行測試。

測試中的工作介質(zhì)為RP-3航空煤油;在出口處安裝節(jié)流閥以調(diào)節(jié)出口壓力,在節(jié)流閥處安裝齒輪流量計進行體積流量的測量,隨后測量航空煤油密度以得出質(zhì)量流量;保持溫度在規(guī)定值的±5 ℃范圍內(nèi);試驗泵由伺服電機驅動。

新型卸荷槽齒輪泵的質(zhì)量流量試驗裝置如圖10所示在試驗過程中,齒輪泵入口壓強保持在0.35 MPa,齒輪泵出口壓強保持在8 MPa,溫度保持在27 ℃,齒輪轉速在5 500 r/min,6 000 r/min,6 500 r/min,7 000 r/min。

圖10 新型卸荷槽齒輪泵的質(zhì)量流量試驗裝置

在4種轉速下,出口流量仿真與試驗對比如表5所示。

表5 出口流量仿真與試驗對比

由表5可知:泵的出口流量與轉速呈線性關系,并且誤差保持在5%左右。

仿真模型結果與試驗結果較為相符,驗證了筆者的模型準確性。

5 結束語

由于通過理論分析和實驗難以獲得高轉速航空燃油齒輪泵的內(nèi)部流場及空化特性,為此,筆者對一種采用了新型卸荷槽結構的航空燃油齒輪泵進行了數(shù)值模擬研究。

首先,基于標準k-ε湍流模型與全空化模型建立數(shù)學模型,筆者研究了新型卸荷槽齒輪泵的性能;然后,在不同轉速下,對新型齒輪泵內(nèi)流場進行了數(shù)值求解,得到了氣體體積分數(shù)、壓力和速度分布,分析了轉速變化對流場的影響;最后,搭建了試驗平臺,進行了不同轉速下流量測試,并對仿真結果進行了驗證。

研究結論如下:

(1)相比無卸荷槽齒輪泵和傳統(tǒng)矩形卸荷槽齒輪泵,在不影響質(zhì)量流量的情況下,筆者所設計的新型卸荷槽齒輪泵能夠有效降低齒輪泵內(nèi)流場的氣體總體體積分數(shù),減弱空化帶來的危害;而且能夠有效降低齒輪泵的脈動系數(shù),提高其輸出流量品質(zhì);

(2)在轉速較高(大于5 000 r/min)的齒輪泵中,其流場的最大壓力(和)最小壓力并非位于齒輪泵的出口或入口,而是位于齒輪的嚙合處,且最大壓力遠大于齒輪出口的設計壓力。由于受到壓差影響,最大的流場速度也出現(xiàn)在齒輪嚙合處。因此,在設計高速齒輪泵時,應考慮內(nèi)流場的壓力和速度分布,從而保證產(chǎn)品的壽命和可靠性;

(3)齒輪轉速從5 000 r/min提升到7 000 r/min的過程中,齒輪泵內(nèi)氣體體積分數(shù)的最大值、最小值和云圖所顯示的氣體分布范圍都在逐漸增大,說明齒輪泵內(nèi)部流場的空化程度也在隨之逐漸增大。因此,在提高送油效率而提高轉速時,也應考慮空化現(xiàn)象對產(chǎn)品的穩(wěn)定和壽命的影響。

在今后的研究中,筆者擬根據(jù)精確的試驗數(shù)據(jù),對全空化模型進行修正,使數(shù)值模擬結果更加符合高轉速航空燃油泵的實際情況,并在此基礎上,對其進行進一步的結構優(yōu)化設計,以便進一步降低齒輪泵的空化現(xiàn)象。