新能源汽車減速器錐軸承預緊量研究*

胡 迪,米承繼,劉祥環,張廣杰

(1.株洲齒輪有限責任公司,湖南 株洲 412000;2.湖南工業大學 機械工程學院,湖南 株洲 412007)

0 引 言

隨著新能源電動汽車的不斷發展,高集成度的多合一電驅總成應用越來越廣泛,對新能源減速器的噪聲和效率的要求也不斷提高。

中間軸、差速器采用錐軸承可以大幅提高減速器強度,同時有效減小中心矩,從而提高減速器集成度。因此,在減速器低速級上,錐軸承已逐漸取代深溝球軸承,得到了越來越廣范的應用。

但是,錐軸承的預緊不僅對軸承的壽命有直接影響[1],跟其噪聲、齒輪強度及效率也有緊密關聯[2-5]。因此,更加精細化的設計是提高錐軸承產品性能和質量的關鍵。

近年來,諸多學者對軸承設計展開了深入研究。中國科學院的王智[6]研究了錐軸承預緊力與系統剛度的關系,以及軸承預緊力、軸承剛度和軸系剛度之間的關系,推導了軸承預緊力與軸系固有頻率之間的數學模型。陳潤霖等人[7]基于瓦塊支點受力平衡,提出了一種彈性支點的圖解設計方法,根據特定工況條件下的動力學性能要求,合理設計了彈性支點的剛度和預緊力等參數。葉超等人[8]提出了一種基于有限元技術的軸承軸向預緊力優化方法,并利用六西格瑪法,對軸承的軸向預緊力進行了優化和可靠性驗證。

然而,由于汽車行駛工況復雜,不同的轉矩會有不同的變形,對錐軸承預緊量的需求也不同,需要對其進行綜合計算評估。

目前,對于錐軸承的預緊設計大多基于軸承壽命需求的考慮,未充分考慮對減速器總成的影響。計算錐軸承預緊量時,未充分考慮安裝狀態到工作狀態時零件的受力變形和受熱變形。缺乏中間軸和差速器軸兩根軸均為錐軸承時,兩軸不同預緊量組合對減速器的性能影響方面的研究[9]。

基于上述原因,筆者建立軸系錐軸承預緊量的理論模型,考慮減速器總成的零件受力及受熱變形,通過傳動系統分析軟件MASTA分析軸系預緊量、軸承效率、齒輪強度,及不同轉矩工況下的軸承變形。

由于齒輪傳遞誤差峰峰值(簡稱傳遞誤差)會直接影響減速器總成的振動,從而影響總成的噪聲,通過分析兩軸錐軸承預緊量與齒輪傳遞誤差的變化規律,由臺架測試驗證噪聲,最后確定減速器錐軸承軸系預緊量。

1 設計模型構建

1.1 軸承預緊模型

新能源汽車減速器一般采用二級齒輪傳動。由于高集成度及大功率密度等要求,對中心距的設計一般較小,限定徑向尺寸下的深溝球軸承強度無法滿足壽命要求,因此,中間軸及差速器一般采用額定動載荷更高的圓錐滾子軸承。在裝配時,在后軸承上選用不同厚度的調整墊片,以調節錐軸承的預緊量。

減速器傳動系模型的軸系結構,如圖1所示。

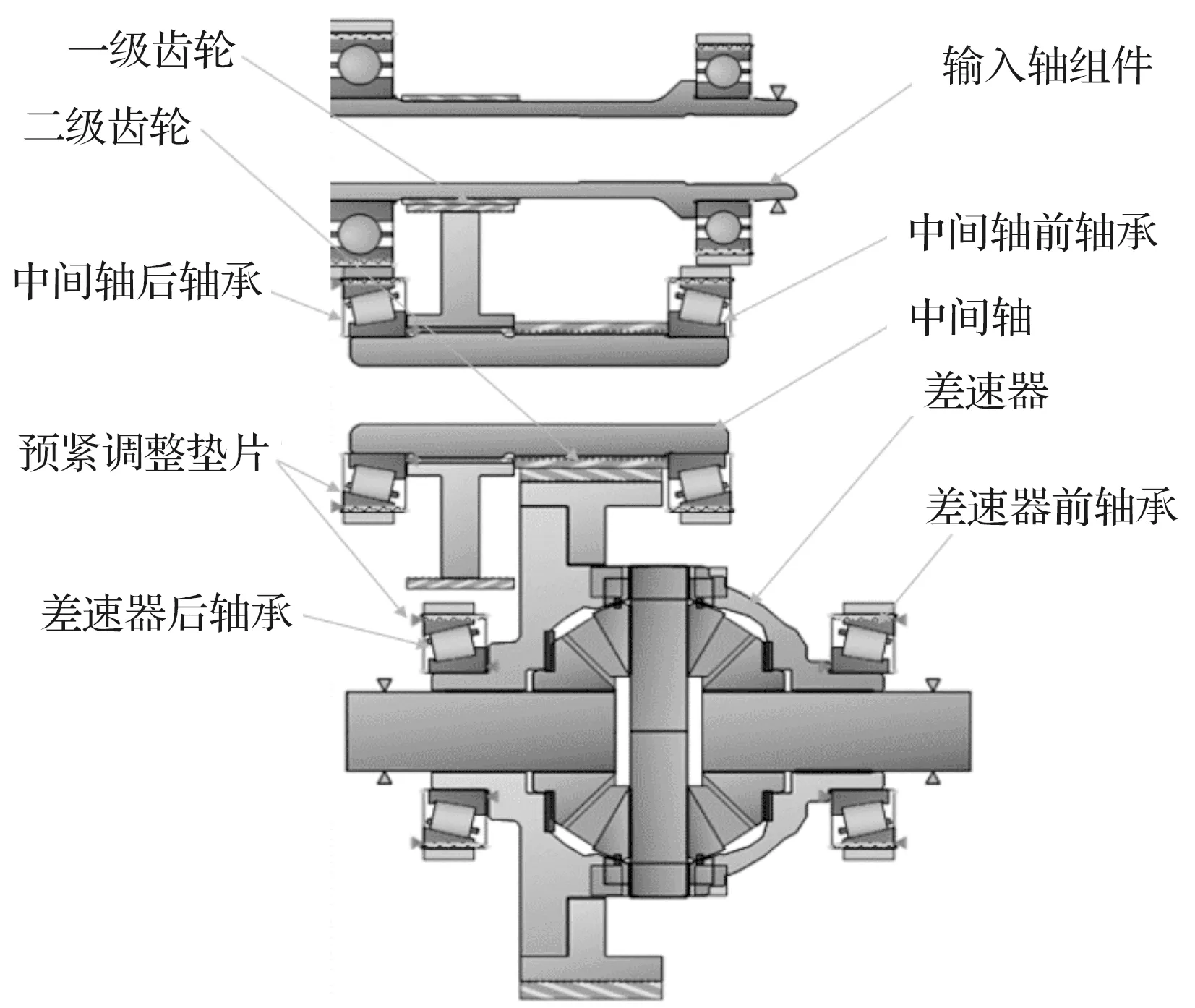
圖1 減速器傳動系模型簡圖

圖1中,減速器輸入軸采用深溝球軸承,中間軸和差速器軸均采用錐軸承。

筆者采用的錐軸承型號為30208,其具體參數如表1所示。

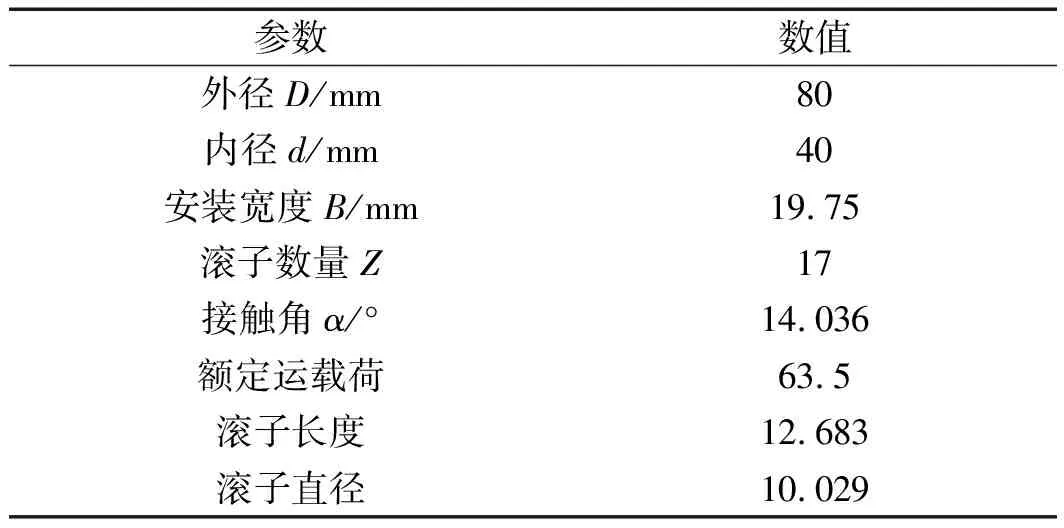
表1 軸承主要結構參數

由于錐軸承的剛度直接影響選片對總成性能的分析結果,需通過試驗測得剛度曲線,如圖2所示。

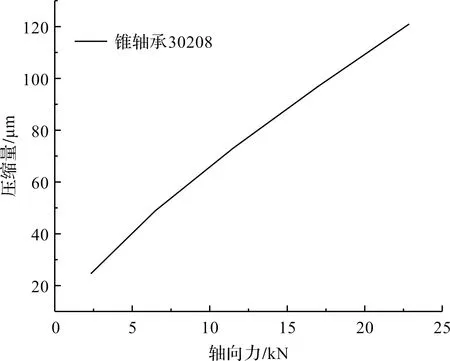
圖2 軸承單體剛度曲線

確定減速器總成設計方案后,筆者搭建MASTA總成模型,并在分析前對模型根據實際情況進行修正。由于差殼和殼體為非線性零件,不同產品有不同結構,受力變形與受熱變形的疊加也不同,兩個軸的預緊量會影響另一軸孔變形,需進行有限元分析。

筆者對差殼、殼體進行全有限元網絡導入進行分析,其結果如圖3所示。

圖3 殼體全有限元模型

齒軸、差殼、殼體材料及相應屬性如表2所示。

表2 零件材料屬性

一般在室溫狀態下,將各零件安裝成減速器總成,安裝溫度取20 ℃,安裝預緊量為初始預緊量。根據文獻[10]及試驗測量,減速器各零件的工作溫度有所差別,其中,油溫80 ℃,軸溫度95 ℃,軸承溫度85 ℃,殼體溫度65 ℃,工作溫度下的預緊量隨之改變。

為了具體分析安裝預緊量與軸承壓縮量之間的關系,筆者將軸組件簡化為錐軸承力學分析模型[11],如圖4所示。

根據受力分析及軸向位移分析,在常溫安裝狀態及工作狀態下,預緊力及預緊量滿足下式:

Fa1=Fa+Fa2

(1)

Fa1=Kh1*xh1=Ka1*δα1

(2)

Fa2=Kh2*xh2=Ka2*δα2

(3)

δ=xh1+xh2+δα1+δα2+xs

(4)

式(1～4)中：δ—軸承預緊量；δa—軸承壓縮量；δT—溫升間隙；δF—受力變形間隙；Fa—斜齒輪軸向力；Fa1—右軸承軸向力；Fa2—左軸承軸向力；Ka—軸承軸向剛度；xh—殼體軸向位移；xs—差殼的軸向位移。

其中，殼體與差殼的軸向位移為受軸向力及受熱變形疊加的結果，可由有限元分析求得，如式xh=f(δTh,δFh)，xs=f(δTs,δFs)。

由于軸承滾子與內外圈受溫度影響時會產生熱膨脹，零部件直徑會發生變化，軸向長度也會增加，直接影響軸承壓縮量δa，其變形滿足下式：

ΔdB=dB*αB(θI-θA)

(5)

ΔDB=DB*αB(θO-θA)

(6)

ΔDW=DW*αW(θW-θA)

(7)

式中：θI—內圈溫度；θO—外圈溫度；θW—滾子溫度；θA—安裝溫度；αW—滾子熱膨脹系數；ΔdB—軸承內徑變化量；ΔDB—軸承外徑變化量；ΔDW—滾子直徑變化量。

實際裝配時，需考慮常溫預緊量以及軸系測量間隙δP，即安裝時的墊片厚度S：

S=δP+δ

(8)

1.2 錐軸承墊片預緊設計

為了確定零件在不同溫度、不同受力下的具體變形量,筆者在MASTA軟件中設定分析工況,使齒軸的Fa=0;通過變形分析,由CAE計算求得相應結果;通過改變單一變量,由不同的溫度單一變量分析可以得到殼體的4個軸承孔軸向受熱變形量,及中間軸與差殼的軸向伸長量。

施加不同的預緊量,則可以得到殼體的4個軸承孔軸向受力變形量,及中間軸與差殼的軸向壓縮量,其結果如圖5所示。

由圖5可以看出:差速器軸的受力和受力變形量均大于中間軸,殼體孔受力變形量小于受熱的變形量。在具體工作時,是兩者的變形疊加,而非其線性的增減。

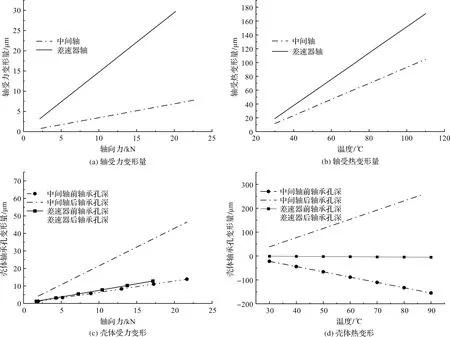
圖5 零件受力變形量及受熱變形量

根據前面提到的工作狀態下的溫度,即軸溫度95 ℃,軸承溫度85 ℃,殼體溫度65 ℃;筆者分析初始安裝溫度狀態下的預緊量與目標工況溫度下0 Nm時的差異,其對比結果如圖6所示。

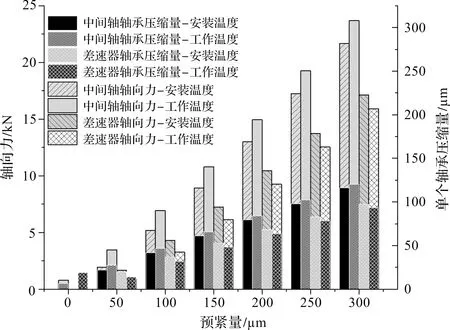
圖6 安裝溫度與工作溫度時預緊結果的變化

由圖6可知:由于軸和殼體受熱、受力變形而相互疊加,工作溫度下的軸承壓縮量大于安裝狀態初始預緊量,預緊結果差異不大。

筆者基于其安裝狀態下的初始預緊量,對分析模型進行雙變量線性掃描,設定2個變量為中間軸后軸承預緊量及差速器后軸承預緊量,設定范圍為-150 μm～300 μm,計算步長為50 μm,輸入轉矩10%、30%、50%、70%、100%,對各工況進行具體的載荷譜分析。

在各工況下,筆者對兩個變量軸承錯位量、齒輪錯位量、齒輪傳遞誤差等相關數據進行分析評估。

不同工況下,軸承內外圈徑向位移與預緊量的關系,如圖7所示。

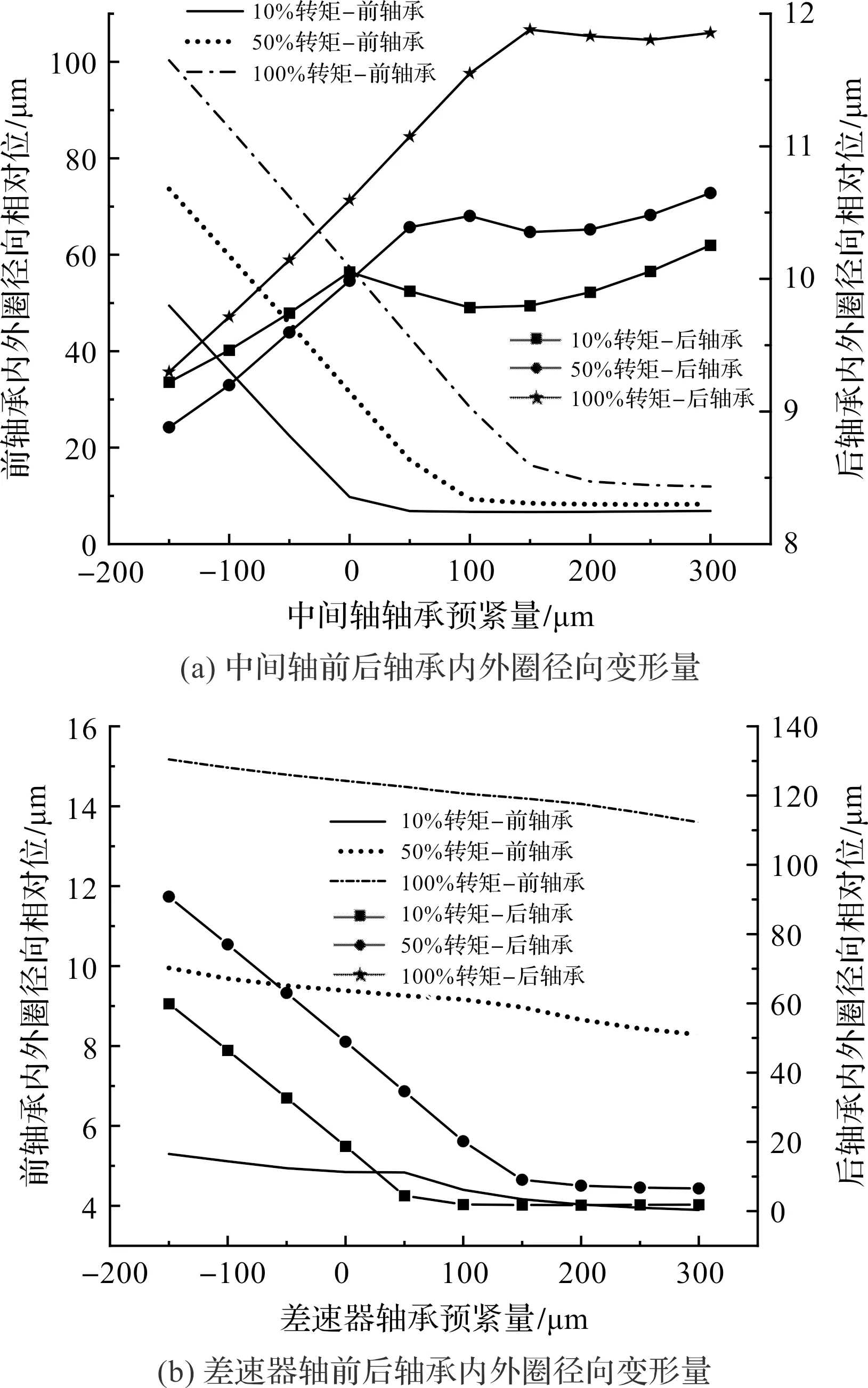
圖7 不同工況下軸承徑向位移與預緊量的關系

由圖7可知:軸承內外圈徑向位移均隨載荷增加而增大。受齒輪軸向力的中間軸后軸承、差速器前軸軸承始終處于軸向預緊狀態,故內外圈徑向位移相對較小;對于不受齒軸軸向力的中間軸前軸承和差速器后軸承,由于僅有派生的軸向力,軸向則為相對放松狀態,內外圈徑向位移相對較大。

這樣就導致兩齒輪軸歪斜,使齒輪附加一個裝配錯位量,會影響產品噪聲情況。不受齒軸軸向力的錐軸承隨著初始預緊量增大,徑向位移隨之減小。

不同工況下,軸承拖曳力矩與預緊量的關系分析結果如圖8所示。

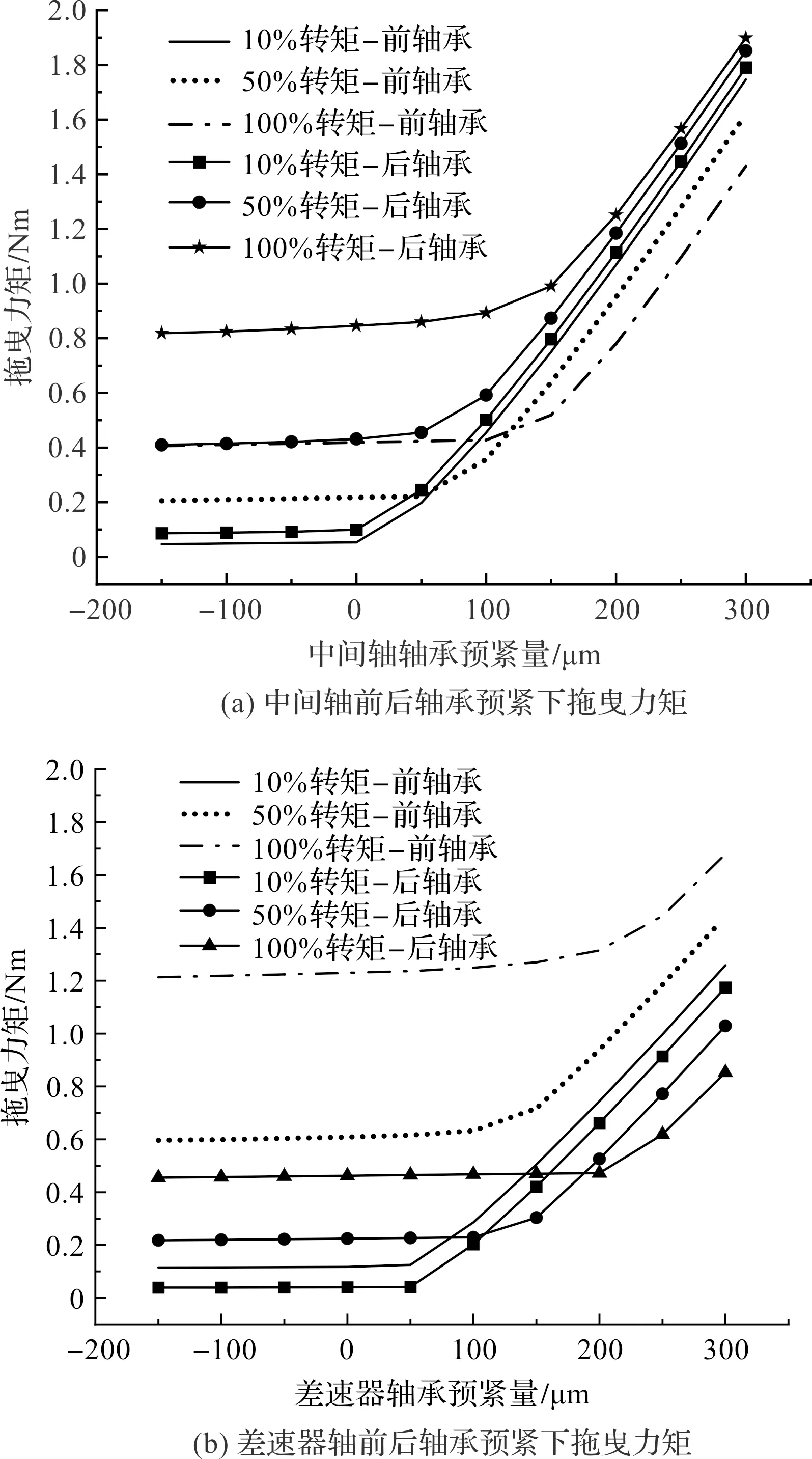
圖8 不同工況下軸承阻力矩與預緊量的關系

由圖8可知:軸承的拖曳力矩隨載荷增加而增大;對于預緊量的增加存在一個拐點,在拐點之前,隨著預緊量增加,拖曳力矩基本無變化,說明預緊量是由力變形導致的;在拐點之后,隨著載荷增加,拖曳力矩迅速增大,從而影響總成效率。

拐點附近為單個軸承實際軸向壓縮量變化的位置,因此,可通過拖曳力矩間接判斷軸承的預緊情況。

以30%轉矩工況為例,軸承軸向剛度與預緊量的關系分析結果如圖9所示。

由于軸承的變形及剛度變化,兩根軸系的4個錐軸承均不相同,對軸上的齒輪也會造成相應的影響,從而影響齒輪錯位量[12]。

在30%轉矩工況下,齒輪錯位量與預緊量關系,如圖10所示。

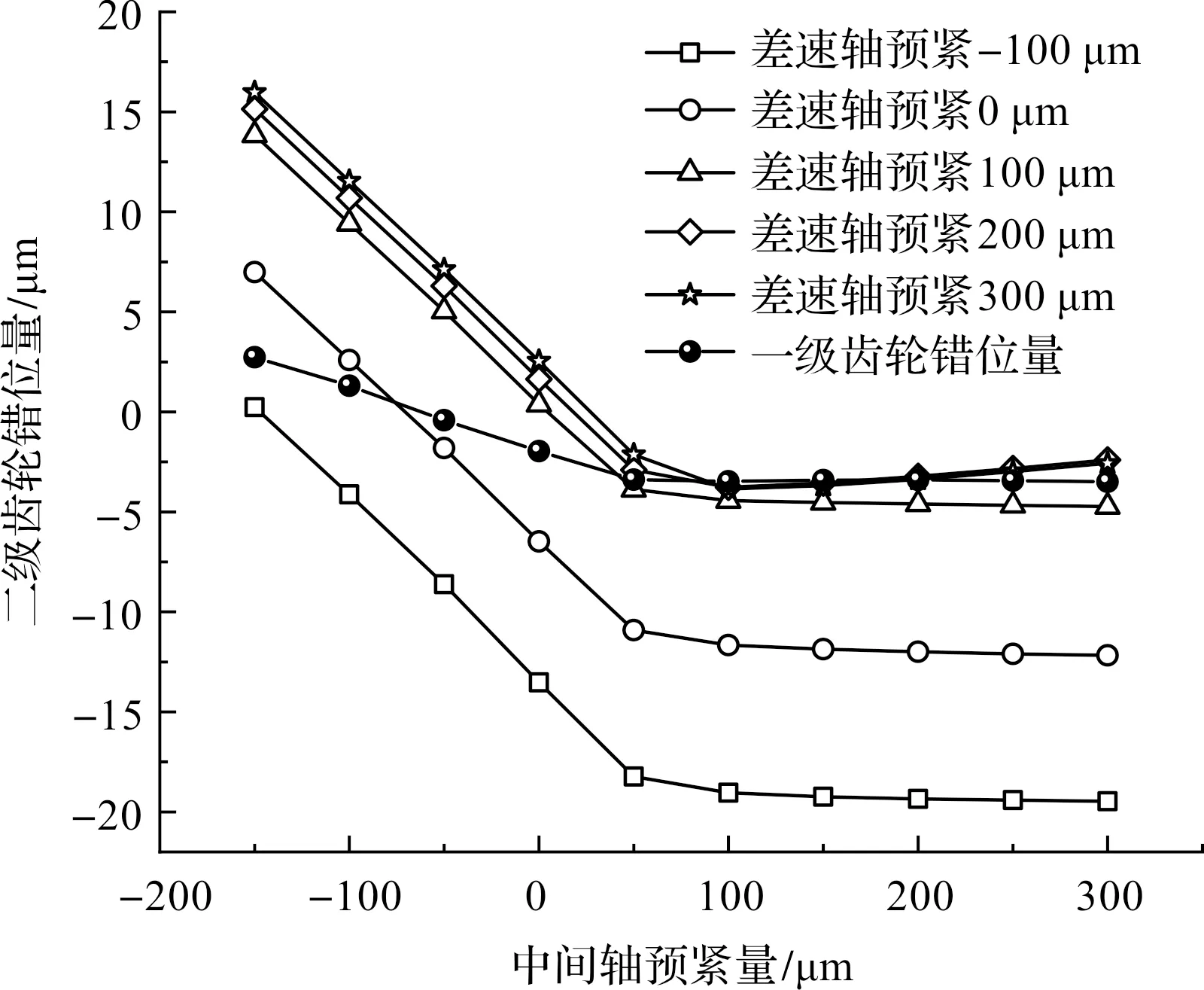
圖10 齒輪錯位量與預緊量的關系

由圖10可知:隨著預緊量的增加,二級齒輪的錯位量減小,進而影響齒向載荷分配系數、齒間載荷分配系數和實際重合度等。

因此,在減速箱總成中,軸系預緊量是否恰當,還需要結合強度、效率和傳遞誤差做進一步的分析,并加以綜合考慮。

2 分析與討論

2.1 預緊量變化規律

首先,筆者根據載荷譜分析兩個變量對新能源汽車減速器各個錐軸承的壽命影響,對新能源汽車減速器效率的影響,及對一級、二級齒輪的強度影響;然后,在輸入轉矩10%、30%、50%、70%、100%工況下,筆者對各工況進行具體的載荷譜分析,對兩個變量在各工況下,軸承錯位量、齒輪錯位量、齒輪傳遞誤差等進行分析評估;之后,對曲型工況進行具體分析,從而綜合評估確定預緊量的區間。

由于不同的預緊量會影響軸承的錯位量、滾子載荷分布等[13-15],需要根據ISO16281修正標準對此進行計算。

根據該文減速器應用的3×105km載荷譜計算結果,可知4個錐軸承的壽命情況,如圖11所示。

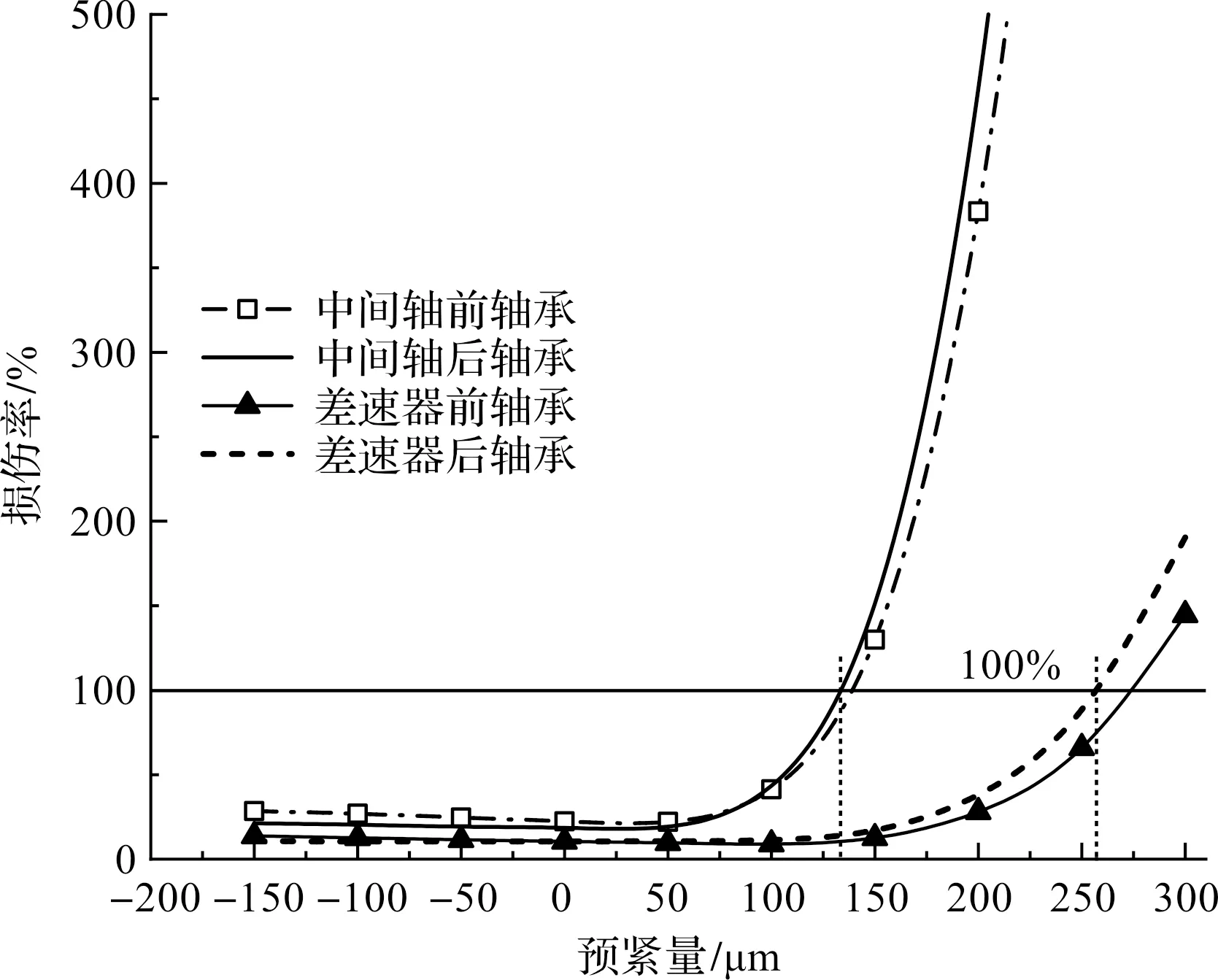
圖11 預緊量與軸承壽命關系

由圖11壽命曲線可知:為保證軸承損傷率在100%以內,通過插值計算后代入模型復核,可得中間軸預緊量需控制在130 μm以內,差速器軸預緊量需控制在250 μm以內。

由于不同的預緊量會導致軸承錯位,從而導致軸的傾斜和齒輪的錯位,影響齒輪的強度,因此,需對其進行分析。

新能源汽車減速器一般采用電機油冷,與減速器共油潤滑;潤滑油黏度很低,FZG等級為7—8級。為提高效率,有必要進行膠合。

在載荷譜計算下,一級齒輪強度與中間軸預緊量的關系,如圖12所示。

圖12 預緊量與一級齒輪強度關系

由圖12可知:一級齒輪的強度隨中間軸預緊量增加而降低,但當預緊量達到150 μm以后,基本趨于穩定,均符合設計要求。

中間軸預緊量不同,導致中間軸的不同變形,會影響二級主動齒輪;同樣,差速軸承預緊量的不同,會主要影響二級從動齒輪,所以二級齒輪的強度并不會像一級齒輪一樣隨預緊量變化而呈線性的變化,需要采用2個參數同時進行分析。

預緊量與二級齒輪強度關系(趨勢)結果,如圖13所示。

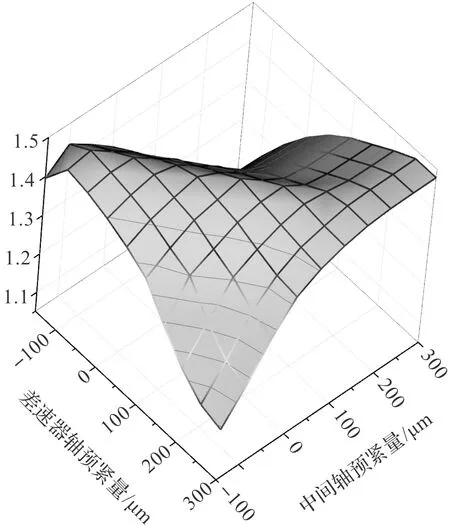
圖13 預緊量與二級齒輪強度關系

由圖13可知:當中間軸與差速器預緊量值相當時,二級齒輪安全系數較高;當一個軸的預緊量很大,而另一個軸的預緊量很小時,齒輪的安全系數變小;當中間軸或差速器軸承預緊量為負值時,即軸向存在間隙時,二級齒輪安全數計算結果小于設計要求值,存在強度風險。

因此,筆者建議兩軸的預緊量均至少控制在0 μm以上。

當軸承預緊量確定時,同樣的拖曳力矩,由于中間軸轉速高,功率損失大于差速器。

不考慮齒輪嚙合損失及攪油損失時,筆者對減速箱總成的所有軸承的總效率進行分析,其結果如圖14所示。

圖14 預緊量與軸承效率關系

由圖14可知:差速軸預緊量在200 μm內,減速器總成軸承效率無明顯下降趨勢;但隨中間軸預緊量的增大,減速器總成軸承效率呈快速下降趨勢。

因此,筆者建議將差速軸的預緊量控制在200 μm以內為宜。

2.2 噪聲分析

首先,在初始安裝預緊量為0時,筆者進行齒面微觀修形,以消除應力集中現象;然后進行不同預緊量下的軸承雙參數耦合計算。

根據上文分析結果(即不同轉矩工況下的齒輪錯位量不同),筆者采用MASTA進一步分析其傳遞誤差及重合度,以評價其對噪聲的影響情況。

一級傳遞誤差與不同工況的預緊量情況如圖15所示。

由圖15可知:當中間軸預緊量達到100 μm后,再增大預緊量對一級齒輪影響較小。

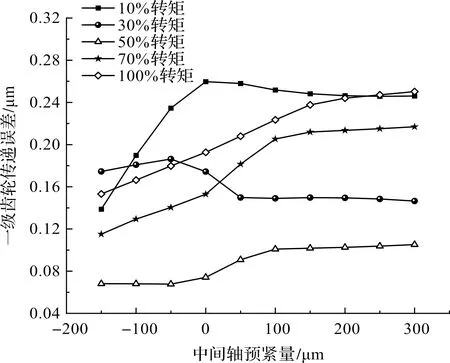
圖15 不同轉矩下預緊量與一級傳遞誤關系

對于一級齒輪,其傳遞誤差主要受中間軸預緊量的影響,當中間軸預緊量達到一定量后,中間軸軸承基本已處于無錯位狀態,增加預緊量不會影響其傳遞誤差。

下面,筆者主要對二級齒輪的噪聲情況進行研究,通過對全工況雙參數進行掃描分析,找出惡劣工況進行具體分析。

預緊量與二級齒輪傳遞誤差關系如圖16所示。

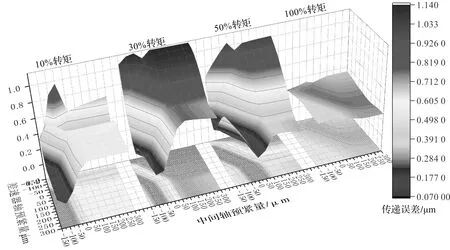
圖16 預緊量與二級齒輪傳遞誤差關系

由圖16傳遞誤差云圖可知:在小轉矩階段,二級齒輪的傳遞誤差隨差速器預緊量的增大而呈現變小的趨勢,隨中間軸預緊量增大而呈現變大的趨勢;到滿載時,系統本身的受載變形已大于軸承預緊產生的變形,故受軸承預緊量的影響較小,并且30%轉矩工況下的傳遞誤差明顯大于其他工況,而該工況一般為整車常用工況。

在30%轉矩工況下,筆者對二級齒輪噪聲情況影響的實際重合度和錯位量的影響進行具體分析,其結果如圖17所示。

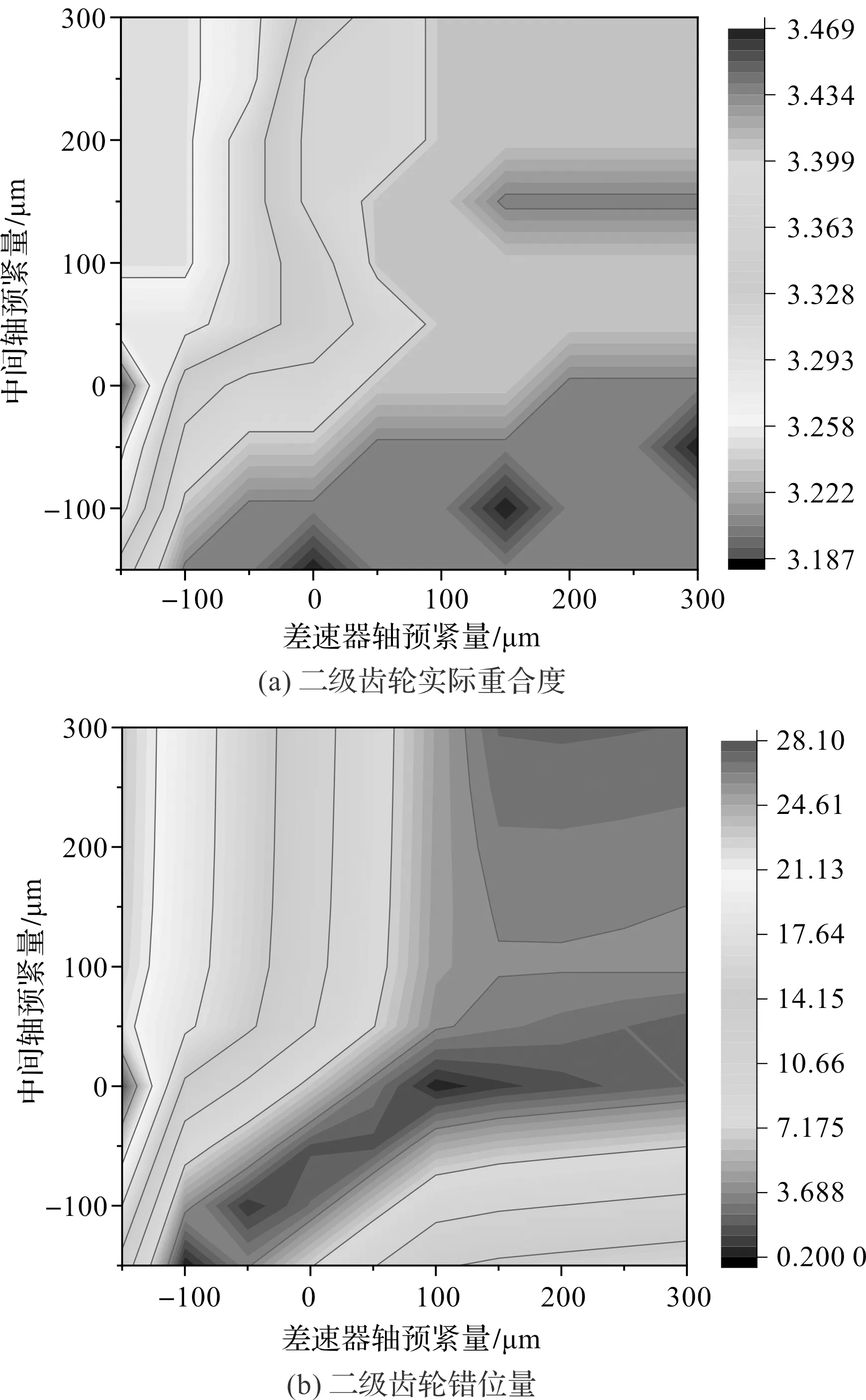
圖17 30%轉矩工況噪聲參數

由圖17可知:二級齒輪實際重合度最大的區域在差速器軸承預緊量偏大值,且中間軸預緊量偏小值處,與齒輪傳遞誤差的趨勢相同;二級齒輪錯位量最大的區域,在兩軸的軸承預緊量值相當處,與齒輪強度計算結果趨勢相同。

30%轉矩工況下,二級齒輪傳遞誤差與兩軸的預緊量關系,如圖18所示。

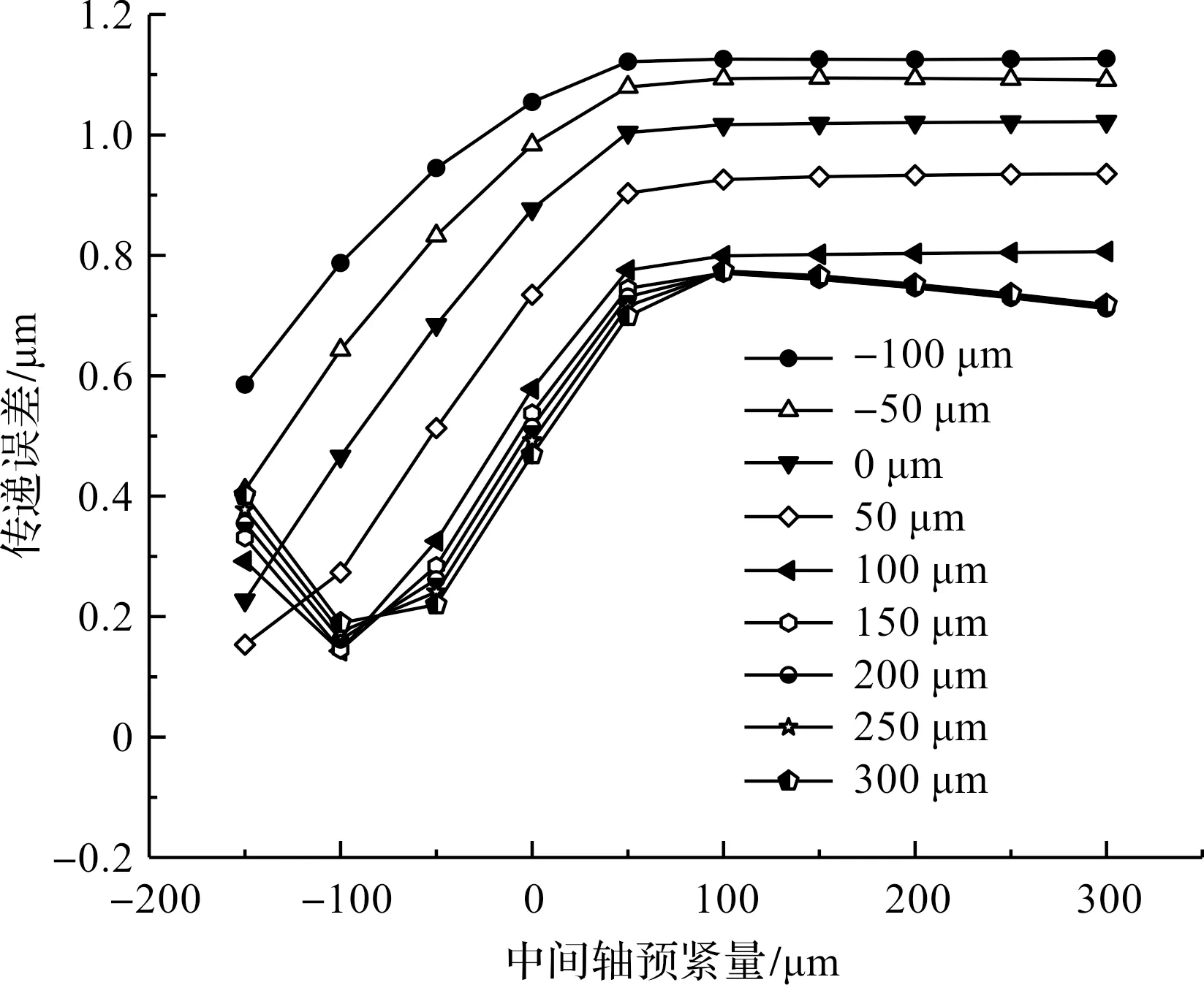
圖18 預緊量與傳遞誤差關系

由圖18分析結果可知:在30%轉矩工況下,差速器軸傳遞誤差隨預緊量增加而降低,達到150 μm后基本穩定;并且傳遞誤差隨中間軸預緊量增加而增大,在中間軸預緊量超過100 μm后基本穩定;但是,其值仍大于其他工況,在30%轉矩工況下,軸承完全預緊時的傳遞誤差仍大于其他工況。該結果說明,還需要進行其他設計優化,如齒輪修形等。

根據上述噪聲分析結果,綜合考慮其效率及壽命、強度情況,再結合生產選片控制精度,筆者建議將該款新能源汽車減速器的差速器軸預緊量控制在100 μm～200 μm以內,中間軸預緊量控制在40 μm～110 μm以內。

3 臺架試驗

對于軸承單體,筆者進行不同預緊力、不同轉速的拖曳試驗,在減速器總成裝配過程中,采用測量差速器軸啟動力矩的方式,以確定錐軸承預緊量是否符設計要求;并進行啟動力矩試驗,以得到不同預緊量下的啟動力矩范圍。

筆者根據前文得到的建議預緊量來考慮預緊公差,按差速器軸150 μm,中間軸50 μm進行裝配。

為了驗證上述測量誤差及仿真偏差,筆者進行了臺架試驗。試驗臺如圖19所示。

圖19 NVH臺架試驗臺

基于軸承的初始設計預緊狀態,筆者換裝不同厚度墊片,并調整預緊量值(保持其余狀態不變),進行臺架測試對比。

以30%轉矩為例,不同預緊量的齒輪階次切片結果,如圖20所示。

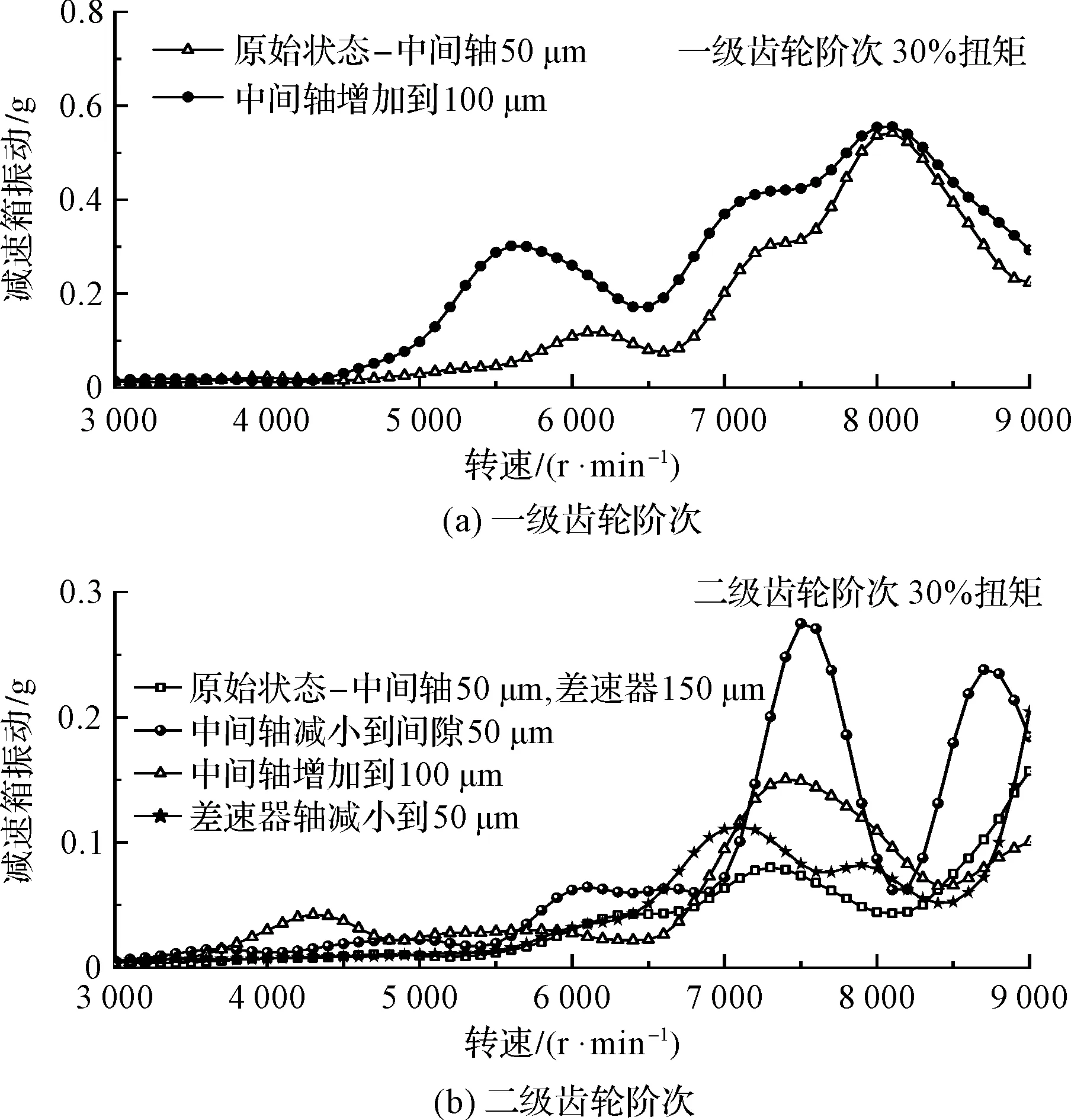
圖20 不同預緊量的齒輪階次切片

由圖20的測試結果可知:在各轉速段中,一級齒輪階次振動隨中間軸承預緊量的增加而增大;由二級齒輪階次振動確定的噪聲情況為,中間軸承預緊量為50 μm(該結果優于預緊量100 μm,且優于間隙50 μm);差速器預緊量減小50 μm后,噪聲略有增加。這說明噪聲的變化趨勢與設計分析結果相符。

最終,根據設計結果進行預緊量裝配的減速箱,通過了減速器總成的效率測試、噪聲測試和總成疲勞耐久試驗。

4 結束語

錐軸承的預緊對減速器的壽命、噪聲、強度及效率有緊密關聯,因此,為了得到最優的產品性能指標,筆者分析了減速器軸系錐軸承預緊量的影響因素,建立了力學分析模型,分析了初始安裝預緊量與工作狀態預緊量的具體差異;通過MASTA仿真模型,根據載荷譜計算了軸系安裝預緊量與軸承的壽命、齒輪強度及效率的關系;根據中間軸和差速器軸雙參數變量掃描分析,研究了預緊量與齒輪錯位量、重合度和傳動誤差的關系。

研究結果表明:

(1)兩軸的預緊量相當時,存在齒輪錯位量越小,其強度越高的趨勢;

(2)總成效率隨中間軸預緊量的增加而顯著降低;而差速器隨中間軸預緊量的增加時,其效率降低不明顯;

(3)在一定范圍內,中間軸預緊量越大,噪聲越大,而差速器軸預緊量越大,噪聲越小;再增加預緊量時,噪聲不再隨之變化;

(4)臺架測試結果表明,二級齒輪階次噪聲在中間軸承的預緊量為50 μm的結果優于預緊量100 μm的,且優于間隙50 μm的;差速器預緊量減小50 μm后,噪聲有所增加,驗證了噪聲變化結果與仿真結果一致。

因此,確定預緊量設計范圍,可以為類似新能源汽車減速器預緊設計提供指導。

因為熱變形對軸承實際預緊量有很大的影響,且差速器與中間軸、相應軸承的實際溫度有較大差異,所以在后續的研究中,筆者將對軸承及相關零件的溫升進行具體分析和驗證,以提高不同溫度下,軸承預緊量分析和設計的準確性,進而提升新能源汽車減速器總成的性能。