葉片質量失諧下整體葉盤的振動響應特性研究*

楊錚鑫,卞天天,黨鵬飛

(沈陽化工大學 機械動力工程學院,遼寧 沈陽 110142)

0 引 言

葉片—輪盤結構簡稱整體葉盤結構,在葉輪機械中起著關鍵的作用。整體葉盤具有循環對稱的結構特點[1],振動模態沿圓周方向均勻一致地分布。

但是在其使用過程中,由于材料離散性、安裝誤差、使用磨損等各方面原因,會導致各扇區在整體葉盤間產生微小差別[2],使其結構的循環對稱性遭到破壞。在結構動力學中,這種結構變異稱為失諧[3]。

在整體葉盤振動過程中,失諧會導致其能量始終集中在一個或幾個葉片上,即振動能量的局部化現象[4]。該現象使失諧葉片的振幅可以達到完整參考葉片振幅的數倍,從而產生局部葉片的高周疲勞(high cycle fatigue,HCF)失效[5],不僅會縮短葉輪機械的使用壽命,而且會造成重大的安全事故。

為了預測整體葉盤在失諧條件下的響應,有效避免葉片HCF風險,學者們對失諧整體葉盤的振動特性,及振動所造成的影響做了大量研究,并取得了許多重要的研究成果[1,6-8]。

近年來,許多學者對含有剛度失諧的葉片響應特性進行了深入的研究。

HUANG B H等人[9]先后采用連續性參數模型模擬的方式,在考慮科氏力效應的情況下,研究了剛度失諧對其葉盤模態局部化的影響。王紅建等人[10]建立了質量—彈簧組合模型,并采用該模型,分析出了剛度失諧后,整體葉盤結構的振動響應特性。YAO Jian-yao等人[11]采用節徑譜方法,對剛度失諧整體葉盤的動態特性進行了測試和模擬,通過分析得到了最優人為失諧(錯頻)規律,以及在剛度隨機失諧情況下,整體葉盤激振力的臨界現象;研究還發現,應用一定的諧波主動失諧[12]進行干涉,能夠使失諧整體葉盤的穩定性進一步得到提高。

然而,以上的研究僅限于處理未發生質量失諧條件下,整體葉盤的失諧問題,而對于葉片—輪盤結構中的質量失諧問題,卻并沒有進行過多的描述,并且很少對整體葉盤各葉片之間(由于質量不均引發)的失諧進行研究。

若將失諧問題僅歸結為簡單的剛度失諧,而忽略質量失諧所帶來的影響,勢必會在失諧整體葉盤動力學特性的分析及模擬過程中,造成失真現象,從而在葉片疲勞損傷檢測方面導致疏漏或誤導[13]。

姚建堯等人[14]在航空航天研究方向的發動機失諧整體葉盤研究中,對失諧結構多種建模分析方法進行了比較,總結出了不同分析方法研究葉盤動力學方向的優缺點。LIM S H等人[15]采用質量—彈簧組合系統模擬分組拉筋結構整體葉盤模型,研究出了具有分組拉筋結構葉盤的振動響應規律[16]。ZHOU Shui-ting等人[17]采用三維有限元方法,建立了葉片拉筋結構的轉子系統模型,分析出了其結構振動特性的響應規律。

在探索轉子動力學方向上,國內外學者應用多種方法,進行了大量深入的研究。

一些學者采用連續參數法,建立了失諧整體葉盤模型,對失諧整體葉盤的振動響應規律進行了研究,且在研究過程中,不僅考慮了葉片的阻尼、裂紋因素,而且還考慮了復合板、帶冠狀等特征,使其對失諧整體葉盤響應特性的分析更加具體。

如HUANG B H等人[18]采用Eular梁與曲梁相結合的方式,對整體葉盤葉片進行模擬,分析出了整體葉盤結構特性規律。但是連續參數模型的模擬是有局限性的,板和梁在模擬過程中,因為存在人為干擾,很難真正模擬實際葉片和葉盤[19]。在某些程度上雖然能夠提高模擬精度,但其模擬精度仍然較低,只適合用于機理研究[20]。

王艾倫等人[21]對失諧葉盤結構振動特性進行了研究,結果發現,葉片裂紋會使整體葉盤的振動特性產生較大的變化;通過建立了集中質量整體葉盤模型,證明了葉片裂紋擴展與失諧整體葉盤振動局部化之間存在關聯。HOU F J等人[22]的研究認為,葉片裂紋會加劇整體葉盤振動的局部化程度;通過建立帶有裂紋葉片的集中質量整體葉盤模型,定性研究了裂紋造成失諧的葉片對整體葉盤結構局部化的影響,并得出結論,即在非強耦合條件下,葉片基頻變化不受小長度裂紋影響,而其結構耦合比和裂紋長度對葉片最大振幅有影響。

因為人為干擾因素,在研究失諧振動,分析了某些失諧葉盤結構頻率轉向、模態局部化、動態響應局部化及振動響應等規律時,集中參數模型會存在模擬精度低等局限性[13,23]。

連續參數法和集中參數法雖然在研究整體葉盤基本振動響應規律起到了很好的作用,但這兩種分析方法同樣存在局限性,在對整體葉盤方向上進行更深層次的研究時,這兩種方法受到了限制。

在整體葉盤結構的進一步發展研究方面,高保真有限元模型的應用顯然更加廣泛。

劉鐵箭等人[24]采用ANSYS,建立了發動機壓氣機葉片的三維有限元模型,并對其葉片進行了動力學分析,通過模擬得到了激振力下葉片的振型及諧波響應,分析了葉片工作轉速下應力最大值出現的位置。Reddy等人采用渦輪-縮減編碼程序,分析了受迫響應結構與氣動耦合的顫振失諧,進行了氣動不穩定和ANSYS結構分析,研究發現,在顫振不穩定時,空氣動力效果最小[25]。

以上學者應用ANSYS三維有限元分析法,探索了轉子結構動力學特性,且均取得了很好的效果。

單個葉片質量失諧方程的建立推導與裂紋葉片導致的整體葉盤失諧方程的建立推導是相似的,因此,可以采用集中質量整體葉盤模型與ANSYS有限元分析結合的方法,以此來研究單個葉片質量失諧下的系統響應變化,以便更準確地反應失諧整體葉盤的振動特性規律。

筆者基于單個葉片失諧的集中質量整體葉盤模型與ANSYS有限元分析,通過模擬葉片在質量失諧條件下的整體葉盤振動響應變化,研究單個葉片質量失諧對系統振動特性的影響規律。

1 失諧葉盤模型及運動方程

筆者建立循環對稱結構的集中質量整體葉盤物理模型,如圖1所示。

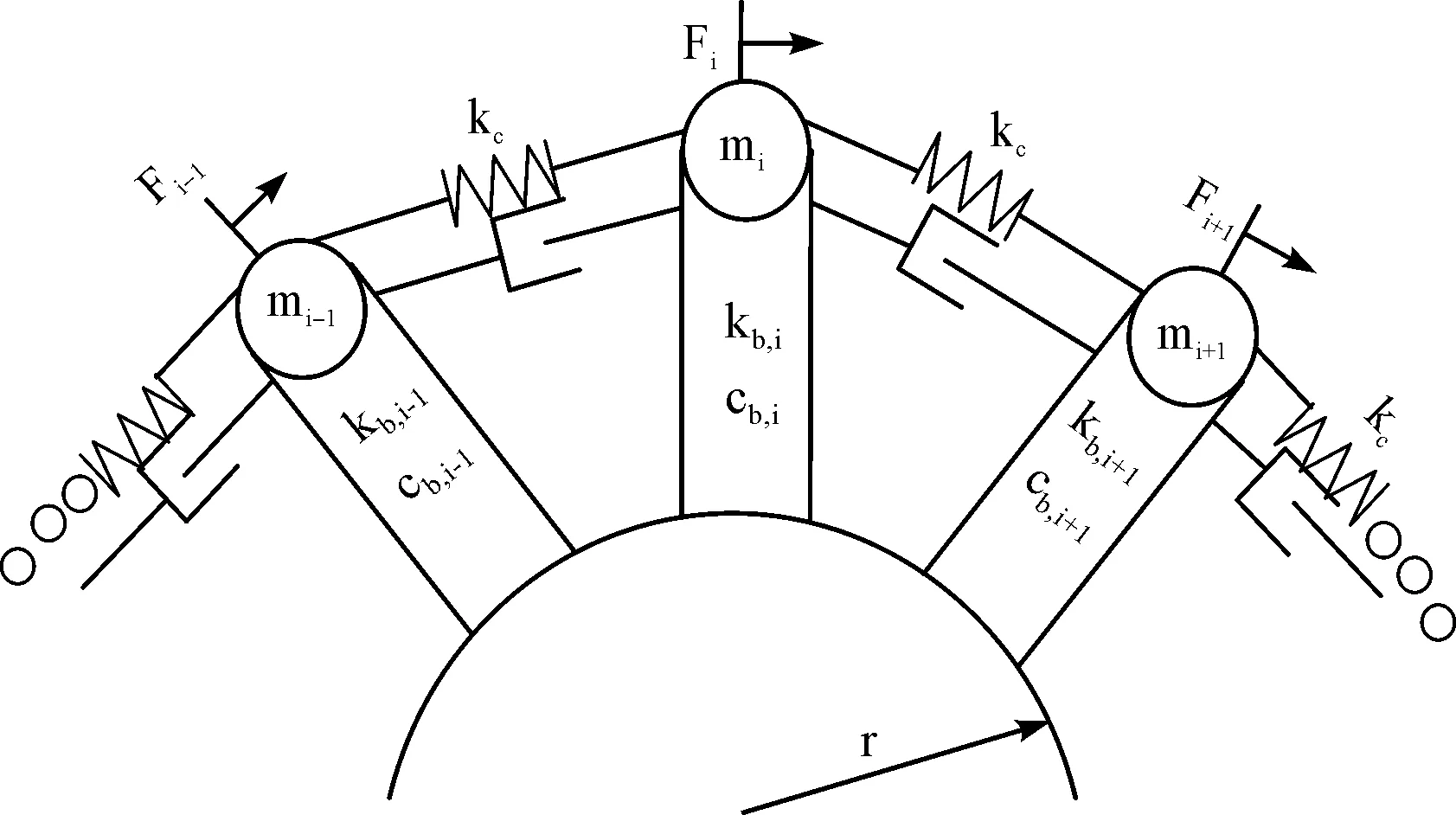
圖1 集中質量整體葉盤物理模型

假設在諧調狀態下,模型是半徑為r的剛性輪盤,N個葉片簡化為固定在輪盤上的集中質量梁,則第j個葉片固有頻率為:

(1)

設葉片自身固有頻率為:

(2)

在不考慮非線性因素,同時阻尼cc=0的情況下,第j個整體葉盤葉片的振動方程可表示為:

(3)

式中:xj—第j個葉片的位移;R—整體葉盤耦合強度;N—等效耦合頻率;N—葉片的自振頻率;Fj—諧調作用在第j個葉片上的激振力;ζ—葉片間阻尼比。

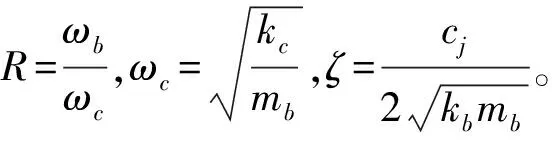
在N個葉片條件下,循環對稱結構的整體葉盤振動方程可用矩陣形式表示,即:

(4)

式中:FT—激振力矩陣;M—質量矩陣;K—剛度矩陣;C—阻尼矩陣;X—位移矩陣。

整體葉盤在工作過程中,由于其旋轉和非旋轉部件會受到氣流擾動的影響,通常將該擾動模擬為加載于諧調葉片上的激振力,因此,其擾動形式可假定為FT:

FT=Feiωt{1,eiΦ1,…eiΦj,…,eiΦN}

(5)

其中:

(6)

式中:Φj—第j個葉片上外力的相角;ω—激振力頻率;E0—激振力的階次。

其中:

XT={x1,x2…xj…xN}

(7)

(8)

(9)

在循環對稱的整體葉盤中,剛度矩陣Kj通常由無損葉片廣義剛度kj和耦合廣義剛度kc組合而成,即Kj=kj+kc。

剛度矩陣K的表達式為:

(10)

對于循環對稱的整體葉盤,所有葉片的質量,阻尼,剛度均相等,即x0≡xN,x1≡xN+1,m1≡mj≡mN。

因此,式(4)可進一步轉化為以下矩陣形式:

(11)

其中,A的表達式為:

(12)

假設整體葉盤的位移為:

X=xeiωt

(13)

將式(13)代入式(11)中,可得到:

(14)

通過式(1～14),采用集中質量整體葉盤物理模型,筆者建立諧調整體葉盤的響應方程。

基于圖1整體葉盤物理模型,假定N個葉片的整體葉盤中,第j個葉片發生了質量失諧,而葉片間耦合阻尼為0,并且根據質量失諧的定義,可得失諧葉片的質量為:mj=(1+ε)m。

因此,在式(4)循環結構葉片的基礎上,可通過增加質量失諧量ε來簡化為下式

(15)

引入質量失諧附加矩陣I0,并將I0代入式(15),可將其轉化為矩陣形式的質量失諧整體葉盤結構振動方程:

(16)

其中,質量失諧附加矩陣I0可表示為:

(17)

式(16)經推導可轉化為質量失諧系統的響應特性方程:

(18)

2 失諧量對整體葉盤幅頻特性的影響

為了研究不同失諧強度、耦合強度、阻尼比等參數下,整體葉盤的質量失諧振動特性響應規律,基于上述的葉盤模型,筆者選定基準值葉片數N=20,耦合強度R=0.1,激振力階次E0=2,阻尼比ζ=0.01;假設第2個葉片出現質量失諧,失諧量ε=0.1;并采用MATLAB進行模擬計算,得到質量失諧情況下,各個參數的響應特征。

取不同失諧量ε,即ε=-0.1、ε=-0.05、ε=0、ε=0.05、ε=0.1情況下,其他參數為初始值(不發生改變)時,系統的振動響應特性,如圖2所示。

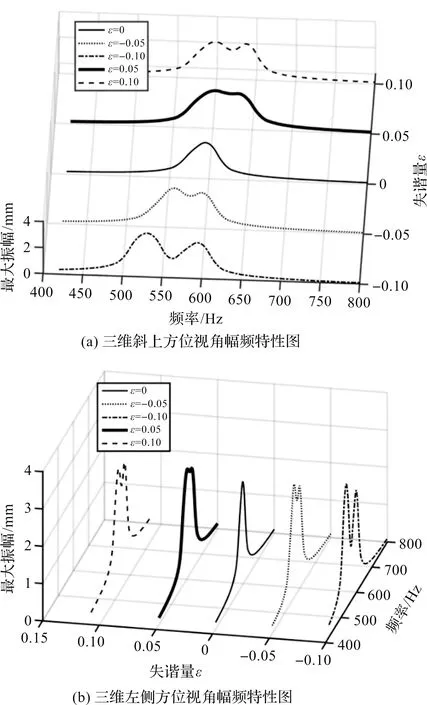
圖2 不同失諧量ε的幅頻特性曲線

從圖2可知:與未失諧的參考葉片ε=0相比,失諧葉片在失諧量ε=-0.1情況下,失諧葉片的共振幅值由初始值2.7 mm增加到3.5 mm,并且出現多余的波峰。這說明,當葉片發生質量失諧時,整體葉盤振動的劇烈程度加劇,破壞了葉盤的穩定性;

質量失諧系統的模態與作用在整體葉盤上的激振力不具有嚴格的正交性,隨著失諧量反向增加至ε=0.1,會出現整體葉盤的次峰值反向移動,大響應幅值的激振頻率范圍有所收斂,但是次峰值仍然存在,整體葉盤的振動仍然不具有穩定性。

3 不同參數整體葉盤幅頻特性的影響

3.1 不同耦合強度R的影響

相比非整體葉盤模型,在質量失諧的整體葉盤條件下,整體葉盤的葉片和輪盤間的耦合關系更強。因此,對輪盤和葉片的振動響應特性進行分析時,應當將其作為一個整體結構[26]。

分別取R=0.1、R=0.2、R=0.3、R=0.4、R=0.5,而其他參數為基準值時,系統的響應幅頻特性圖,如圖3所示。

圖3 不同耦合強度R下的幅頻特性曲線

由圖3(a)可知:耦合強度R增大,會使系統的最大響應峰值向右偏移。該現象說明：隨著耦合強度R增大,整體葉盤的剛度增加,使系統的固有頻率也跟著增加;

在低耦合R=0.1條件下,系統的響應激振頻率變化范圍更廣,激振敏感區變化范圍在450 Hz～650 Hz;低耦合向中高耦合R=0.4過渡時,激振敏感區縮減至500 Hz～650 Hz。這一現象說明,在低耦合條件下,失諧整體葉盤對失諧條件更加敏感。

由圖3(b)可知:當耦合強度R從0.1增加到0.2時,系統的響應峰值出現增加趨勢;而當耦合強度R從0.2增加到0.5的過程中,系統的響應峰值出現了降低。該現象說明,在低耦合條件下,增大失諧系統耦合數會使系統響應幅值增大;而在高耦合條件下,增大耦合強度會降低系統的響應峰值,從而起到了一定的積極作用。

以上現象表明,僅依靠單方面增加耦合強度,不能有效地控制系統的響應幅值。

3.2 不同阻尼比ζ的影響

當失諧整體葉盤的阻尼發生改變,即ζ=0.001、ζ=0.004、ζ=0.006、ζ=0.008、ζ=0.01時(其余基準值不變),質量失諧整體葉盤的幅頻特性曲線,如圖4所示。

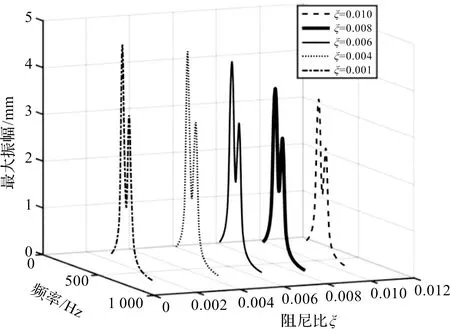
圖4 不同阻尼比ζ的幅頻特性曲線

圖4中,當阻尼比增大時,質量失諧整體葉盤的振動幅值會相應地降低。阻尼系統是工程師為有效地降低葉盤的振動,提高葉盤疲勞壽命而設計的一種結構,它對于減小葉盤(由于失諧引起)振動可以起到促進作用[27]。

在單個葉片質量失諧的整體葉盤同樣是適用的,阻尼比的增加使得系統除主峰值外的其余峰值變化趨于平緩,各波峰間的峰值差減小,即波峰鈍化現象。該現象表明,系統阻尼的增大仍對改善失諧整體葉盤的振動響應具有促進作用。

4 ANSYS仿真模擬及驗證

由于使用三維有限元分析法能夠更精確地描述失諧整體葉盤的振動特性,筆者采用ANSYS建立三維失諧整體葉盤結構模型,如圖5所示。

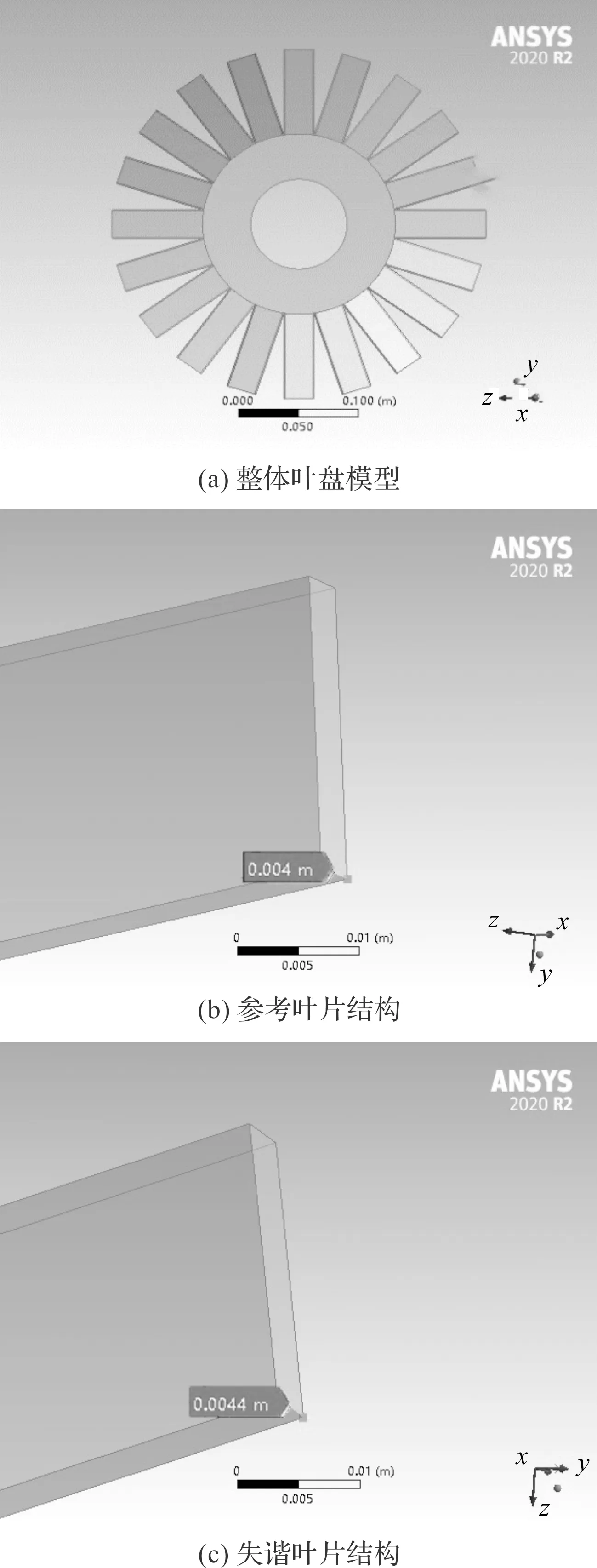
圖5 失諧葉盤有限元模型

筆者通過改變葉片幾何結構的方式,削減葉片厚度,使用ANSYS模擬葉片質量失諧,對整體葉盤進行諧響應分析,得到失諧葉片及不同參數在葉片質量失諧下的響應特性曲線。

其中,不同失諧量ε下的幅頻特性曲線如圖6所示。

圖6 不同失諧量ε下的幅頻特性曲線

不同耦合強度R下的幅頻特性曲線如圖7所示。

圖7 不同耦合強度R下的幅頻特性曲線

不同阻尼比ζ下的幅頻特性曲線如圖8所示。

圖8 不同阻尼比ζ下的幅頻特性曲線

由圖(6～8)可知:

在研究葉片質量失諧對整體葉盤的振動響應時,采用集中質量法與有限元分析法,所得結果仍然會存在小范圍的誤差,但兩種方法所得到的響應特性規律基本吻合,不影響最后的判斷結果。

5 結束語

葉輪機械的整體葉盤中,由于葉片質量的分布不均,會產生葉片質量失諧、振動局部化等問題,為此,筆者對失諧整體葉盤的振動響應特性規律進行了研究。首先,建立了整體葉盤物理模型,繪制出了不同葉盤參數下的幅頻特性曲線;然后,建立了不同葉片厚度的整體葉盤三維有限元模型,對其振動響應特性進行了分析,并繪制出了幅頻特性圖;最后,總結出了各項參數對系統振動特性的影響規律。

研究結論如下:

(1)單個葉片質量失諧很大程度上會破壞整體葉盤結構正常工作的穩定性,使整體葉盤系統的振幅有所增加,并且出現多余峰值,在幅頻特性曲線上可以很好地體現出來;

(2)耦合強度對于質量失諧整體葉盤的振動特性有非常重要的影響,不同耦合強度的工作環境,其響應幅值變化趨勢也不同。在低耦合強度下,質量失諧對系統的響應更加敏感;在某些情況下,改變耦合強度會對系統產生一定的積極效果;使系統振幅減小,響應頻率變化范圍也會根據耦合強度的大小進行調整;

(3)改善阻尼對優化失諧整體葉盤的幅頻特性具有促進作用,增大整體葉盤的阻尼比能夠有效地減小系統的響應振幅。在設計和制造葉盤的過程中,可以通過控制整體葉盤耦合強度和阻尼比,使系統遠離共振區域,延長葉輪機械的使用壽命。

在葉片質量失諧整體葉盤的實際工作環境中,需要充分地考慮各種葉盤參數條件下的失諧系統振動響應特性。因此,在后續的工作中,筆者將對此進行更進一步的探索。