雙立柱堆垛機結構分析與優化*

馬朝鵬,謝 暉,2,3*

(1.湖南大學 汽車車身先進設計制造國家重點實驗室,湖南 長沙 410082;2.大捷智能科技(廣東)有限公司,廣東 佛山 528225;3.季華實驗室,廣東 佛山 528200)

0 引 言

雙立柱巷道式堆垛機是立體化倉庫的核心設備。隨著科技水平的進步和生產效率的提高,立體化倉庫的整體性能也逐漸提高,包括額定載荷的增大、運行速度的提升以及運送貨物尺寸的加大等。

在堆垛機啟動、加減速和停止時,由于雙立柱巷道式堆垛機自身及貨物的重力,會在機械結構內產生巨大慣性力,并造成應力集中,使載貨臺、立柱或橫梁等關鍵結構件產生彎曲、扭轉變形,長期以往會造成其疲勞現象,最終影響立體化倉庫的穩定運行[1,2]。

因此,為了保證堆垛機運行的剛強度和運動穩定性,對堆垛機進行動靜態分析和結構優化十分重要。

近些年,由于立體化倉庫運用逐漸普及,國內外學者對堆垛機結構仿真及結構優化進行了一系列研究。衛巍等人[3]針對單立柱堆垛機的立柱和橫梁進行了力學模型的建立和剛強度分析,根據分析結果判斷了危險部位,建立了多目標優化模型,并使用MATLAB遺傳算法工具箱進行了結構優化。章真雄等人[4]分析了堆垛機在3種工況下的受力情況,通過給立柱加筋板,以及在立柱腹板兩側開孔這兩種設計,對存在問題進行了改進。黃超等人[5]改變立柱的界面尺寸,通過實驗的方式,對堆垛機結構進行了優化。

目前,國內外堆垛機結構優化的相關研究取得很多成果,但優化方法傳統且單一,僅對堆垛機的某一零件進行結構優化,無法做到全局最優。

筆者以某型號雙立柱堆垛機為研究對象,對其進行靜力學分析和模態分析,然后通過多目標優化的方式對堆垛機龍門結構進行結構優化,使堆垛機整體性能達到最優。

1 概 況

雙立柱巷道式堆垛機結構如圖1所示。

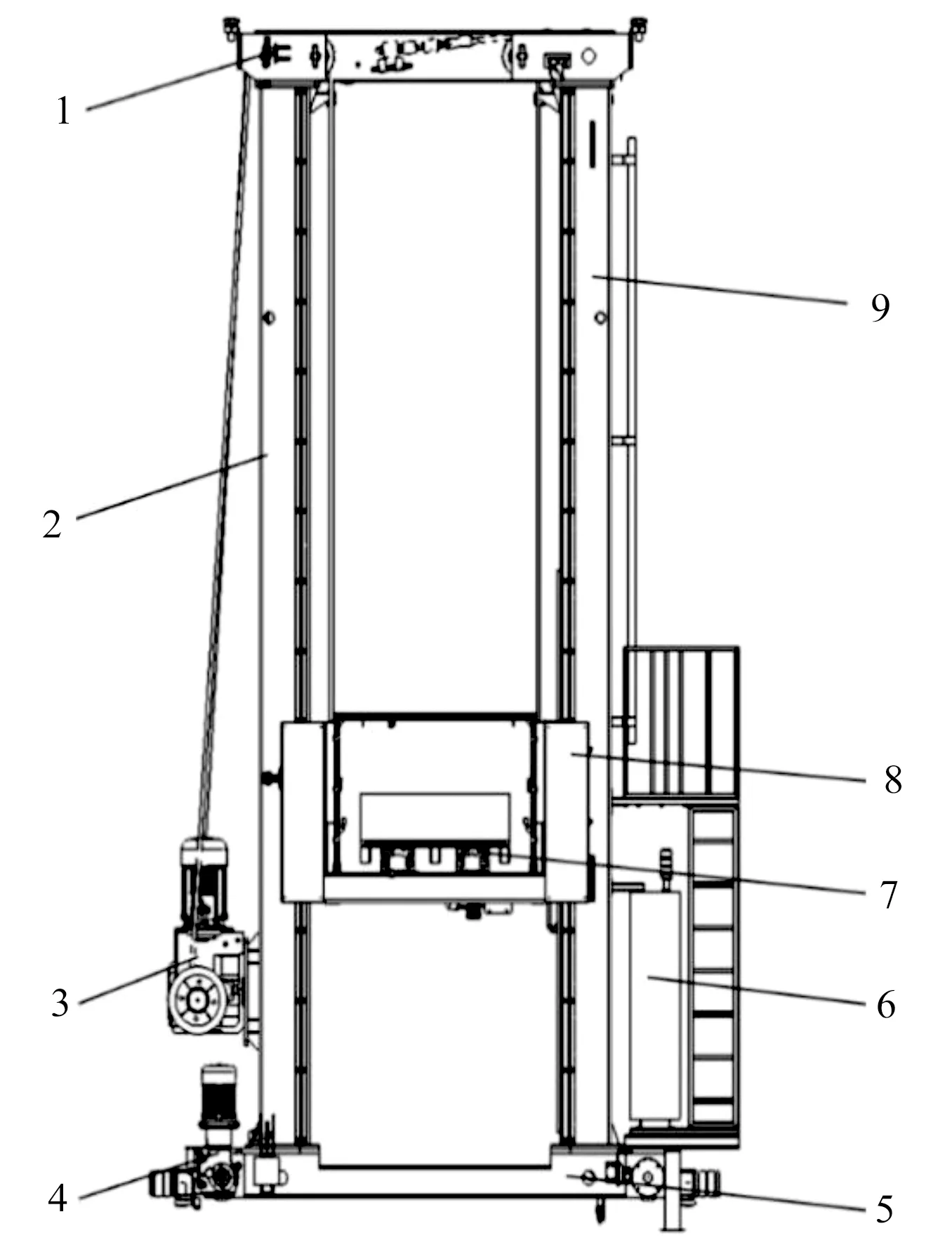
圖1 雙立柱巷道式堆垛機結構圖

圖1主要參數如下:額定載重3 000 kg,載貨臺質量770 kg,升降機構質量250 kg。標準工況下,水平運行速度2 m/s,水平運行加速度0.3 m/s2,升降速度0.3 m/s,升降加速度0.3 m/s2。

2 有限元分析預處理

2.1 模型簡化與導入

由于雙立柱堆垛機的結構復雜,零件種類和數量眾多,所以在進行有限元分析之前,需要對模型進行必要的簡化。

筆者著重研究了龍門結構和載貨臺等關鍵核心部件的受力變形情況,將一些不影響主要研究的零部件簡化,如電氣設備、控制柜、皮帶、軸承等。同時,去除模型中的無關倒角和螺紋孔簡化模型。

筆者使用Solid works完成以上簡化工作,以減少后期網格數量和計算機計算量[6]。在完成簡化后,將模型導入Workbench中。

2.2 材料特性和單元屬性定義

由于Q235A結構鋼良好的焊接性能,該型號堆垛機的結構部件均使用該材料。筆者定義材料屬性為:彈性模量210 GPa,密度7 800 kg/m3,屈服強度235 MPa,泊松比0.26。

另外,堆垛機的金屬框架均為規則的方形管或鋼板,所以在劃分網格時,使用性能完善的自適應劃分網格,即系統根據模型的具體情況決定使用四面體或六面體進行網格劃分[7]。堆垛機龍門機構(上橫梁、下橫梁、左立柱、右立柱)的材料厚度基本為10 mm,載貨臺的材料厚度基本為8 mm,兩者的厚度不同,為了在確保有限元計算精度的同時保證計算速度,堆垛機的網格尺寸大小不做統一化處理。

筆者分別使用50 mm、45 mm、40 mm、35 mm和30 mm依次遞減的網格尺寸劃分龍門結構,使用30 mm、25 mm、20 mm、15 mm和10 mm依次遞減的網格尺寸劃分載貨臺和貨叉。

經過多輪的計算實驗可得,當龍門結構的網格尺寸≤40 mm、載貨臺和貨叉的網格尺寸≤20 mm時,堆垛機的應力和變形基本收斂到某個小區間。所以,根據以上分析結果,筆者設置龍門結構(上橫梁、下橫梁、左立柱、右立柱)的網格最大尺寸為40 mm,載貨臺和貨叉的網格最大尺寸為20 mm。

整體網格劃分結果如圖2所示。

圖2 網格劃分情況

2.3 約束和載荷施加

筆者首先規定,堆垛機沿巷道移動的方向為X方向,載貨臺的升降方向為Y方向,貨叉的伸縮方向為Z方向,坐標系如圖2所示。

由于堆垛機在不同工況下,其受力和變形情況有差異,應選擇受力變形較大的情況進行分析。當載貨臺處于最高位,貨叉完全伸出時,堆垛機處于較危險的狀態[8]。此時,應約束下橫梁X,Y,Z3個方向自由度。另外,上橫梁保留Y軸移動自由度和Z軸的旋轉自由度,也應約束其他方向自由度。

通過對堆垛機施加沿Y軸負向、大小為9.8 m/s2的重力加速度,實現堆垛機重力加載;在托盤上施加沿Y軸負向3 000 kg等量的力;上橫梁的6個定滑輪承擔了載貨臺和貨物的重量,因此,對每個定滑輪的受力按照實際受力比例進行分配;載貨臺上的兩個大滑輪牽引載貨臺的起升工作,因此,它們平分載貨臺和貨物的重量。

3 堆垛機有限元分析

3.1 靜應力分析

3.1.1 變形分析

筆者應用Workbench軟件中Static Structural模塊,得到堆垛機整機的變形云圖,如圖3所示。

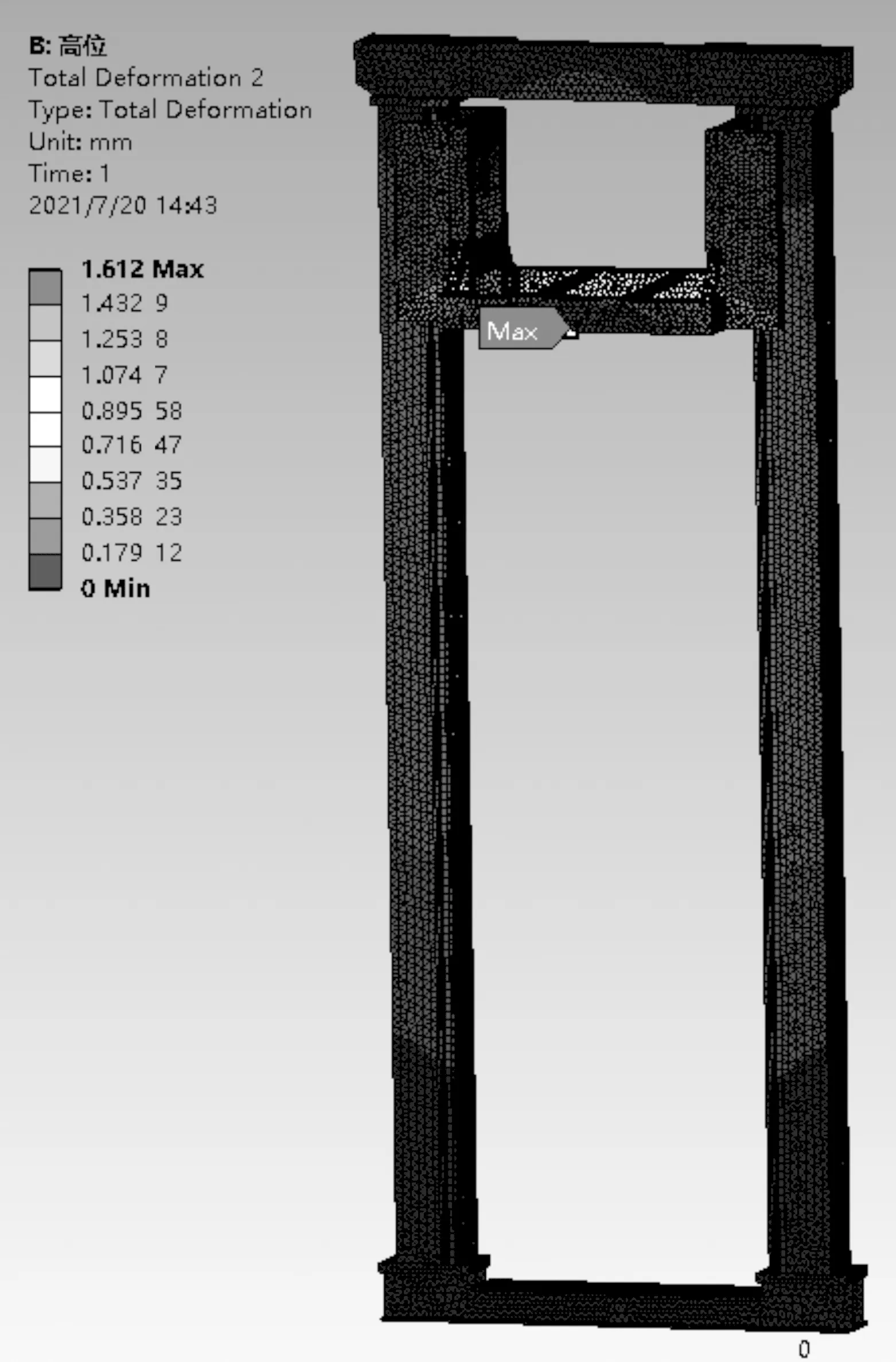
圖3 堆垛機整體變形云圖

在滿載工況下,堆垛機整機結構最大變形量為1.612 mm。

載貨臺的變形云圖如圖4所示。

圖4 載貨臺變形云圖

由4圖可知:堆垛機的變形最大位置也就是載貨臺的變形最大位置,出現于載貨臺的前橫梁;此時貨叉伸縮結構完全伸出,且貨物位于貨叉頂端,載貨臺為保持水平方向的平衡,承受貨物帶來的彎矩作用,與貨叉前端接觸的載貨臺前橫梁位置變形最大,但其變形量較小,因此,其對堆垛機的正常使用沒有影響。此外,載貨臺的變形呈現左右對稱。

龍門結構的變形云圖如圖5所示。

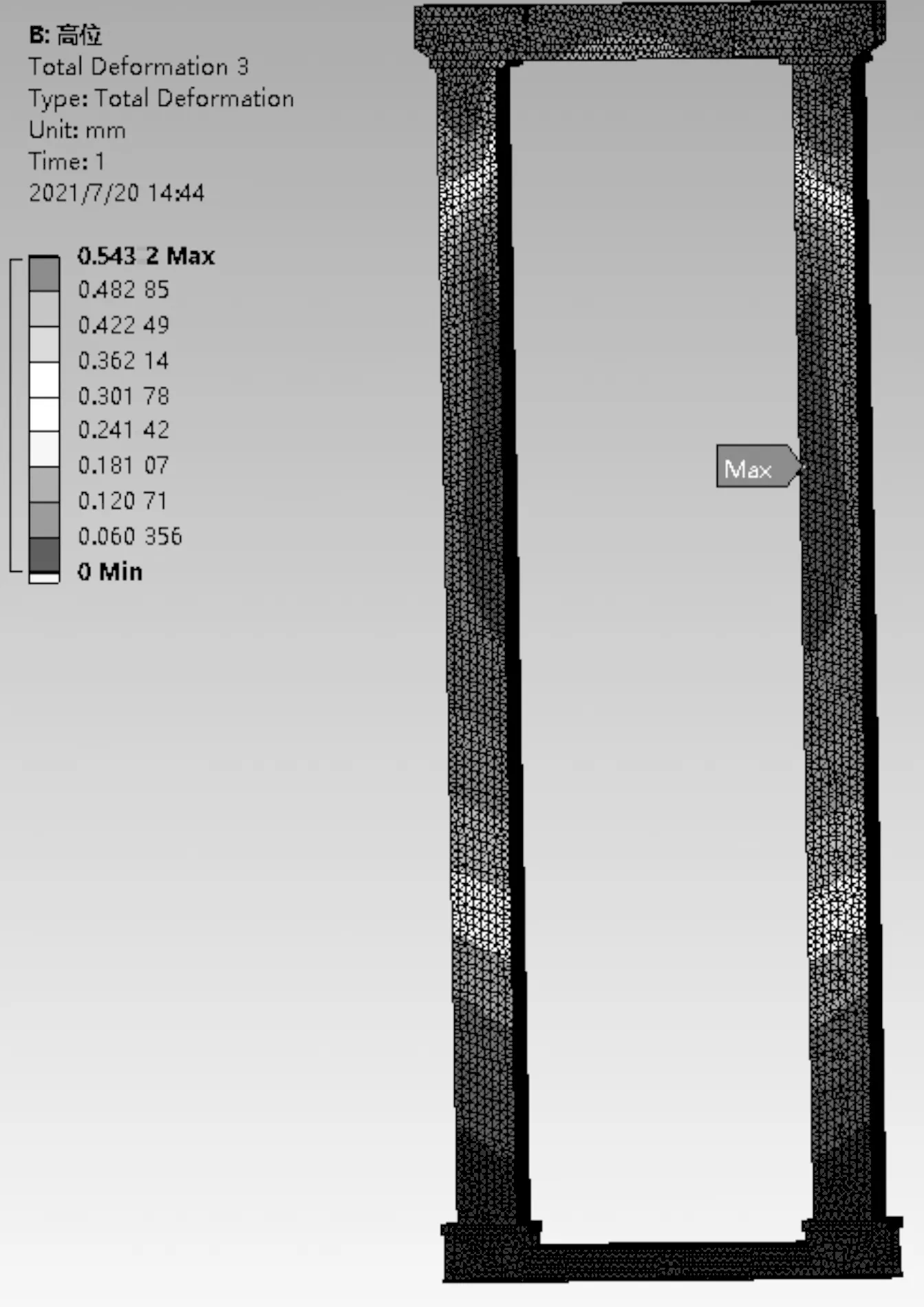
圖5 龍門結構變形云圖

龍門結構的最大變形量出現在左右立柱中段,大小為0.543 2 mm,原因是貨物的重力產生的彎矩對立柱產生拉伸作用[9]。另外,左右立柱的變形量依舊呈現左右對稱,也間接說明整個堆垛機結構有對稱性,不會出現重心偏置帶來的傾倒風險。

《JBT 7016—2017巷道堆垛起重機》對堆垛機立柱的靜剛度值做了性能要求,即“當起升高度不大于10 m時,其靜剛度值應不大于H/2 000(H為堆垛機全高);當起升高度大于10 m時,其靜剛度值應不大于H/1 500”,而靜剛度的定義為結構在特定的靜態激擾下抵抗變形的能力,一般用結構在靜載荷下的變形多少來衡量,所以選取堆垛機最大變形量作為檢驗堆垛機靜剛度的指標。

根據此國標設計原則,當堆垛機高度不大于10 m時,靜剛度值應不大于H/2 000=3.7 mm(該型號堆垛機全高7.4 m)。根據前文分析,本型號堆垛機在滿載情況下的靜剛度值為0.543 2 mm,沒有超過堆垛機的許用靜剛度值3.7 mm,滿足剛度的要求。

3.1.2 應力分析

雙立柱巷道堆垛機結構的等效應力云圖如圖6所示。

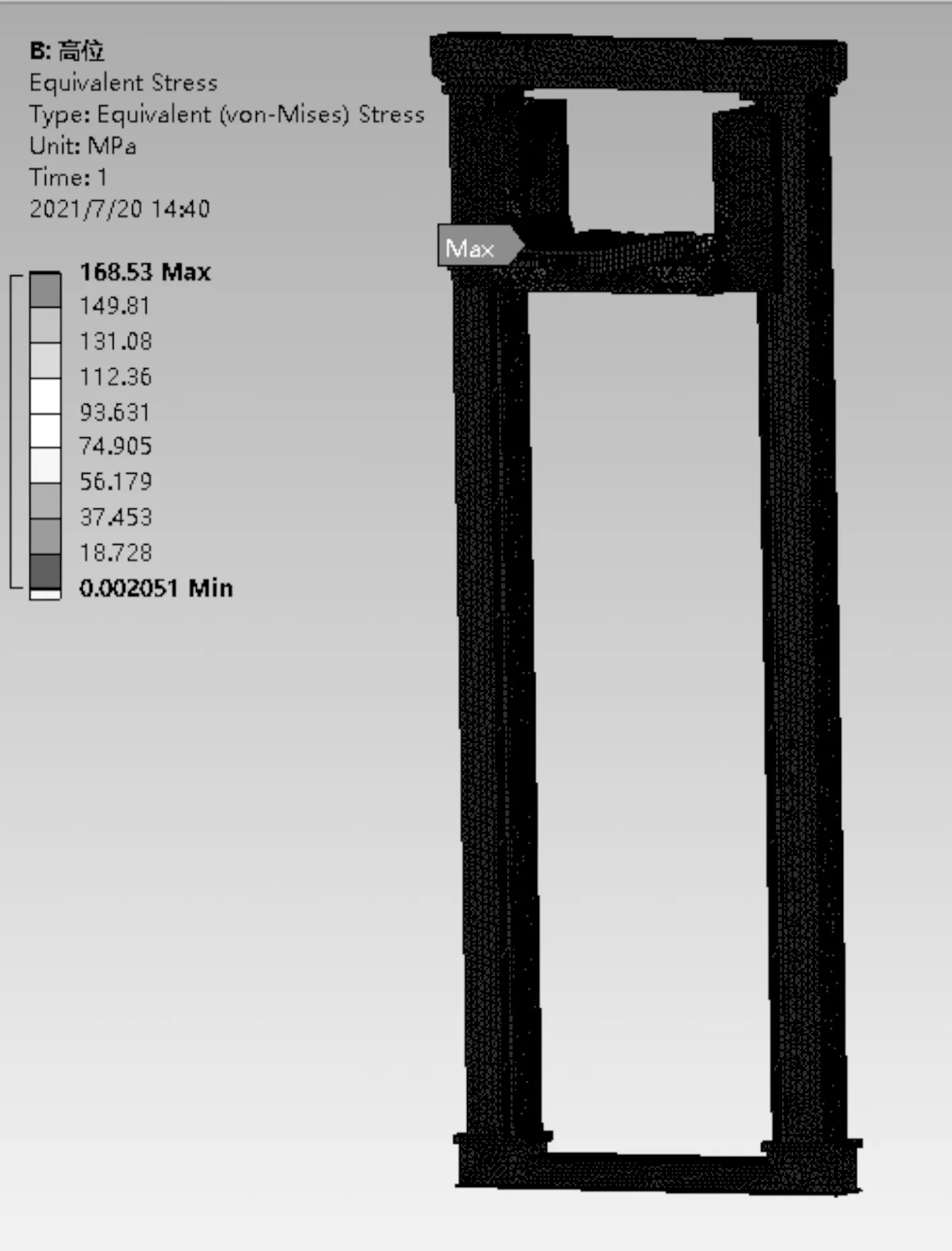
圖6 堆垛機整體應力云圖

在滿載條件下,堆垛機等效應力的最大值為168.53 MPa。

載貨臺的等效應力如圖7所示。

圖7中:最大應力位于載貨臺的下矩形管與垂直框架的連接處,原因是伸出的貨物對載貨臺產生的彎矩使矩形管受到擠壓,而此連接處原設計為直角連接,因此,有限元計算存在應力奇異,計算結果無法隨網格精細程度的提高而穩定到某一區間,需要添加圓角才能做到精密計算;

最大應力小于Q235的許用應力σs=235 MPa,所以載貨臺的強度符合要求。

龍門結構的等效應力如圖8所示。

圖8 龍門結構應力云圖

由于下橫梁承擔整個堆垛機的重量(包括載貨臺和貨物),所以龍門結構的最大應力出現在立柱與下橫梁的連接處,大小為17.811 MPa。國標《GBT 3811—2008起重機設計規范》中對堆垛機龍門結構強度校核做了相關規定。框架結構的應力安全系數s為1.4,許用應力[σ]=σs/[s]=167 MPa,龍門結構最大應力遠遠小于材料許用應力,強度符合要求。

3.2 模態分析

堆垛機運行穩定性由其動態特性決定,因此,在堆垛機設計校核階段需要對其進行模態分析[10]。筆者運用ANSYS有限元軟件,對堆垛機進行了空載運行下的模態分析,既可以得到堆垛機在不同階段的固有頻率和相應振型,也為之后結構優化提供數據支撐。

由于高階頻率對堆垛機結構的影響較小,研究意義不大,所以在選定工況下,筆者只計算了堆垛機的前6階固有頻率和相應振型,如圖9所示。

圖9 堆垛機前6階模態振型圖

分析圖9可知:

第一階頻率為14.142 Hz,立柱發生彎曲變形,表現為沿Z方向的擺動;第二階頻率為24.69 Hz,堆垛機主要變形發生在立柱上,表現為沿X方向的擺動,同時因為載貨臺與立柱相接觸,所以會伴隨產生變形;第三階頻率為24.828 Hz,立柱產生沿X方向的彎曲變形;第四階頻率為33.612 Hz,右立柱發生較大變形,表現為沿Y方向的扭轉;第五階頻率為39.352 Hz,最大變形發生在左右立柱中部,為1.004 4 mm;第六階頻率為43.367 Hz,變形主要發生在載貨臺,表現為在XOY平面的彎曲。

由以上分析可知:前六階模態振型的振動變形較小,固有頻率較高。模態分析是結構設計校核階段避免機器產生共振現象的有效手段。自動化倉庫堆垛機行走的上下巷道不是一段完整的鋼軌,是由很多段鋼軌焊接到一起。由于導軌的焊縫不平整,堆垛機的外界振動主要來源于堆垛機水平方向運動時,車輪與焊縫的接觸。

筆者根據《JBT 9018—2011自動化立體倉庫設計規范》對堆垛機水平方向速度做了規定:速度處于24 m/min～250 m/min之間,而筆者項目規定該型號堆垛機水平運行速度為2 m/s,位于此區間內。

由于堆垛機的底部輪之間的距離為3 420 mm,所以激振頻率為0.58 Hz,遠遠小于第一階固有頻率14.142 Hz,故堆垛機可以有效避免共振情況發生[11]。

4 結構優化

由上述動靜態分析結果可得:堆垛機在標準工況下,強度和剛度均滿足設計要求。作為核心部件的龍門結構,其承受的載荷最大,質量占比65%以上。因此,筆者將在保證龍門結構剛強度的前提下,以龍門結構的輕量化為主要優化目標,對堆垛機的龍門結構進行改進。

4.1 尺寸參數靈敏度分析

4.1.1 模型參數化

雙立柱堆垛機龍門結構由左立柱、右立柱、上橫梁和下橫梁4部分組成。筆者將通過調整各組成部分的尺寸,實現堆垛機的整體最優性能。

龍門結構參數優化需要參數化的結構有限元模型。在ANSYS優化分析過程中,模型建立和結果提取均通過參數實現,在進行大量尺寸迭代計算時,無需手工修改模型,可有效提高運算效率。

筆者通過將模型導入Solid works中,使用軟件幾何參數設置功能,將對目標函數影響較大的尺寸設置為變量;然后,將參數化的模型導入到Workbench中進行靜力學分析,設置最大應力、最大變形和質量為優化目標。

堆垛機龍門結構的設計變量如圖10所示。

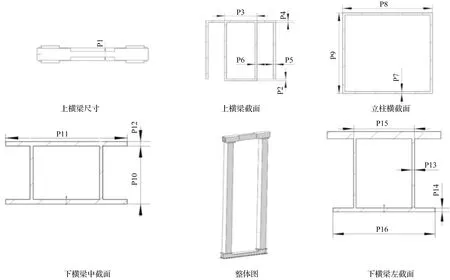
圖10 參數化模型尺寸圖

4.1.2 靈敏度分析

筆者設置堆垛機龍門結構最大應力、結構質量和最大變形為響應目標,運用Workbench軟件中的Response surface模塊,分析各個變量對響應目標的靈敏度,通過多次取樣擬合分析,得到16個變量(P1～P16)對響應目標的影響程度,即靈敏度,將其繪制為靈敏度曲線圖,如圖11所示[12,13]。

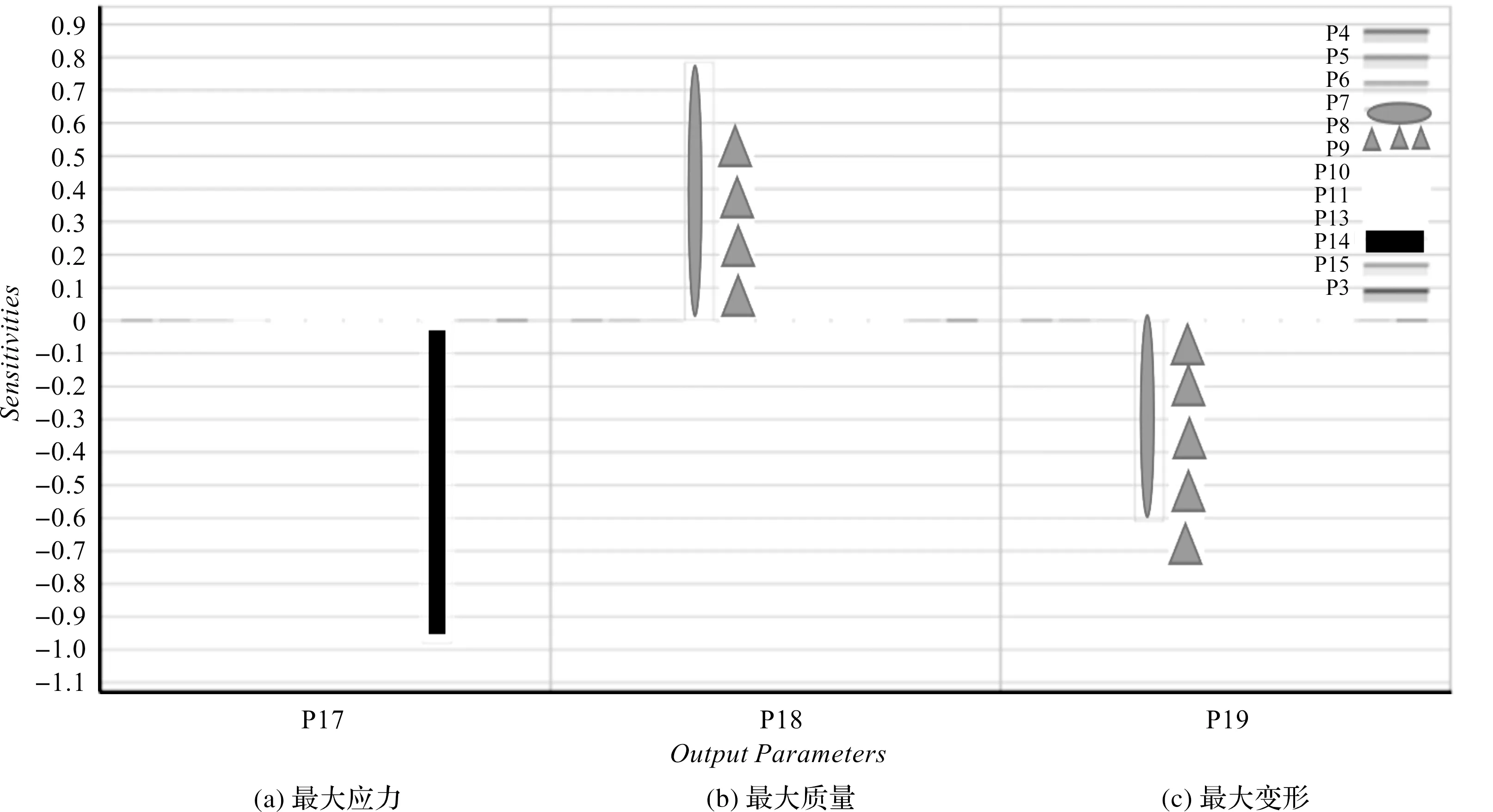
圖11 設計變量靈敏度

圖11(a～c)分別為各個變量對響應目標最大應力、最大質量和最大變形的靈敏度。從圖(a)可以看出,P14對堆垛機的最大應力影響最大;在圖(b)中,P7、P8對堆垛機龍門結構的結構質量影響顯著;圖(c)中,P8對堆垛機最大變形影響最大,P7次之。

因此,設計參數中P7、P8、P14這3個變量對3個響應目標函數值影響較大,筆者選其為優化變量[14]。

4.2 優化模型建立

筆者基于雙立柱堆垛機結構模型,建立以立柱厚度P7、立柱寬度P8和下橫梁底板厚度P14為設計參數,堆垛機質量、結構強度和剛度為優化目標的多目標優化模型,模型如下:

Min(m,σmax,smax)

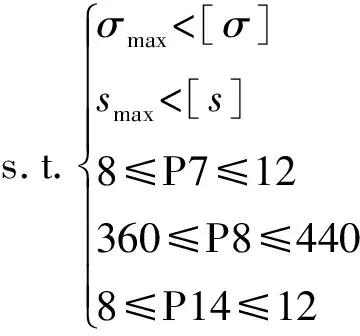
式中:m—堆垛機質量;smax—堆垛機結構的最大變形量;σmax—堆垛機最大應力值;[σ]—堆垛機設計規范中的許用應力值為167 MPa(見3.12);[s]—堆垛機設計規范中立柱的許用變形值為3.7 mm(見3.11);Pi—設計參數[15-18],i=1,2,…16。

4.3 優化結果分析

由于該型號雙立柱堆垛機結構較大,有限元模型單元數量較大,為提高雙立柱堆垛機的優化效率[19],筆者采用最佳填充空間(OSF)設計實驗,使樣本點均勻分配在設計區間,實現較少實驗點對設計參數計算;其次,使用Kriging代理模型模擬輸入輸出函數模型,實現對非線性函數的精準描述;然后,使用MOGA多目標優化方法,以減少優化計算時間,保證了優化的收斂穩定性。

MOGA參數設置如下:初始樣本數量3 000,最大允許的Pareto百分比為70%,收斂穩定率為2%。

通過Workbench的多目標優化,得到3個Pareto最優設計方案,如表1所示。

表1 3個最優Pareto解

分析表1的3種優化方案可知:

方案1對龍門結構的最大變形值優化結果最好,較初始值降低2.53%,方案3、方案2變形量增大;方案2對龍門結構的最大應力優化效果最好,較初始值降低7.40%,方案1、方案3優化效果次之;方案3對龍門結構的質量優化效果最為明顯,較初始值降低6.03%,方案2次之,方案1的龍門結構質量反而增加。

根據本次優化目標及以上的分析可知:第3組方案的優化效果最佳。通過對第3組方案圓整后的最優解與初始解相對比可得到優化前后對比表,如表2所示。

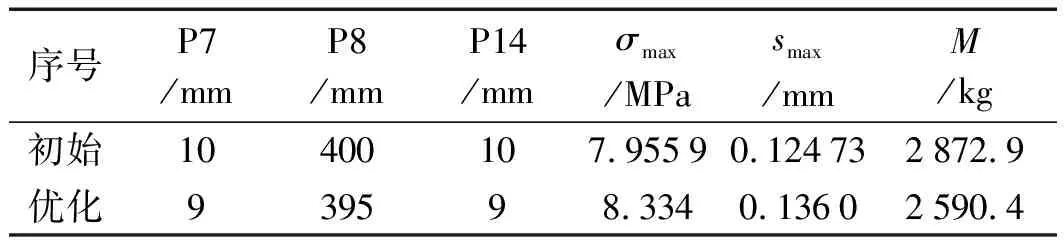
表2 優化前后對比表

雖然堆垛機龍門結構的最大應力增加4.82%,變形增大9.02%,但其強度、剛度仍在許用范圍內,質量卻降低了9.83%,從而實現了堆垛機龍門結構的輕量化。

5 結束語

針對雙立柱堆垛機存在的問題,筆者以某型號雙立柱堆垛機為例,對堆垛機龍門結構進行了優化,以使堆垛機的整體性能達到最優,即使用Workbench軟件對雙立柱堆垛機進行靜力學方法和模態分析方法分析,研究了結構的受力、變形和振動情況;使用多目標優化方法對龍門結構進行了結構優化。

研究結果表明:

(1)基于有限元分析的方法,通過堆垛機整機進行靜力學分析和模態分析,證明當前型號的堆垛機的剛度和強度滿足設計標準,且龍門結構的力學性能有很大冗余量,明確了堆垛機的龍門結構作為堆垛機優化對象的優化方向;

(2)針對堆垛機龍門結構的優化目標,使用Solid works建立龍門結構的參數化模型,采用Kriging建立其代理模型,通過MOGA多目標優化算法求解,獲得了多組最優解;通過比較分析,得到最優的一組解,并對最優值進行了驗證。

優化后的堆垛機龍門結構質量降低了9.83%,最大等效應力和最大變形量在立柱的許用變形范圍內,達到了預期的優化效果。

筆者后續將對堆垛機動力學進行分析研究,并對堆垛機進行運動學仿真，以模擬其真實運動,進一步優化堆垛機的性能。