表面粗糙度對(duì)三叉桿滑球式萬(wàn)向聯(lián)軸器彈流潤(rùn)滑特性的影響*

趙海霞 魏 昆 于夢(mèng)恬 張 宇

(青島科技大學(xué)機(jī)電工程學(xué)院 山東青島 266061)

早期對(duì)彈流潤(rùn)滑的研究大多是基于光滑平整的表面，但是實(shí)際上的潤(rùn)滑表面不可能絕對(duì)光滑，表面總會(huì)存在許多形狀不規(guī)則的微型凸峰和凹谷，這導(dǎo)致潤(rùn)滑的壓力和膜厚改變[1-2]。三叉桿聯(lián)軸器[3]內(nèi)部傳遞元件與滑道之間存在較大作用力，容易產(chǎn)生磨損[4-5]。由于三叉桿聯(lián)軸器彈流潤(rùn)滑的潤(rùn)滑膜厚度非常薄，因此在研究聯(lián)軸器油潤(rùn)滑線接觸等溫彈流潤(rùn)滑的特性時(shí)需要考慮表面粗糙度的影響。

近年來(lái)，關(guān)于粗糙度對(duì)彈流潤(rùn)滑影響的研究不斷發(fā)展。CHRISTENSEN[6]建立隨機(jī)模型，對(duì)具有連續(xù)粗糙峰而且沒(méi)有大量端泄的單面粗糙度表面提出一種修正的雷諾方程；TALLIAN[7]在彈流潤(rùn)滑中加入粗糙度，提出混合彈流潤(rùn)滑理論；PATIR和CHENG[8]考慮到表面粗糙度的因素，把流量因子考慮其中用以修正Reynolds方程，并推導(dǎo)了平均Reynolds方程；黃平和溫詩(shī)鑄[9]采用數(shù)值方法研究了隨機(jī)粗糙度表面在不同載荷和粗糙度條件下的彈流潤(rùn)滑問(wèn)題；MASJEDI和KHONSARI[10]根據(jù)粗糙峰接觸模型建立了線接觸混合潤(rùn)滑模型；王志堅(jiān)等[11]考慮表面粗糙度和潤(rùn)滑油性質(zhì)研究了有限長(zhǎng)線接觸副混合潤(rùn)滑特性。

目前有關(guān)表面粗糙度對(duì)三叉桿式萬(wàn)向聯(lián)軸器影響的研究已有相關(guān)報(bào)道，但并不全面。龐雪彬[12]和周燁[13]在牛頓流體條件下研究粗糙度對(duì)三叉桿滑移型萬(wàn)向聯(lián)軸器摩擦潤(rùn)滑的影響；徐雨田[14]在牛頓流體條件下研究粗糙度對(duì)新型三叉桿滑塊式萬(wàn)向聯(lián)軸器摩擦潤(rùn)滑的影響，進(jìn)行了等溫和熱彈流潤(rùn)滑分析。

三叉桿滑球式萬(wàn)向聯(lián)軸器[15]是一種新型三叉桿式萬(wàn)向聯(lián)軸器。張獻(xiàn)偉[16]已經(jīng)對(duì)其進(jìn)行了動(dòng)力學(xué)與力學(xué)分析，并優(yōu)化了滑球和三叉桿的結(jié)構(gòu)，并對(duì)其在等溫和溫升條件下的脂潤(rùn)滑特性進(jìn)行了分析，但并未考慮到表面粗糙度對(duì)三叉桿滑球式萬(wàn)向聯(lián)軸器摩擦潤(rùn)滑的影響。

因此，本文作者建立了三叉桿滑球式萬(wàn)向聯(lián)軸器等溫線接觸彈流潤(rùn)滑數(shù)值分析模型，改變滑球的表面粗糙度的幅度和間距，在不同表面粗糙度的條件下研究三叉桿滑球式萬(wàn)向聯(lián)軸器的油潤(rùn)滑特性。

1 數(shù)值模型

1.1 建立數(shù)值模型

1.1.1 三叉桿滑球式萬(wàn)向聯(lián)軸器的幾何模型

三叉桿滑球式萬(wàn)向聯(lián)軸器的結(jié)構(gòu)如圖1所示，其主要構(gòu)成部分是輸入軸、滑球、三叉桿、輸出軸，其中滑球與滑球滑道的接觸部位是磨損主要范圍。

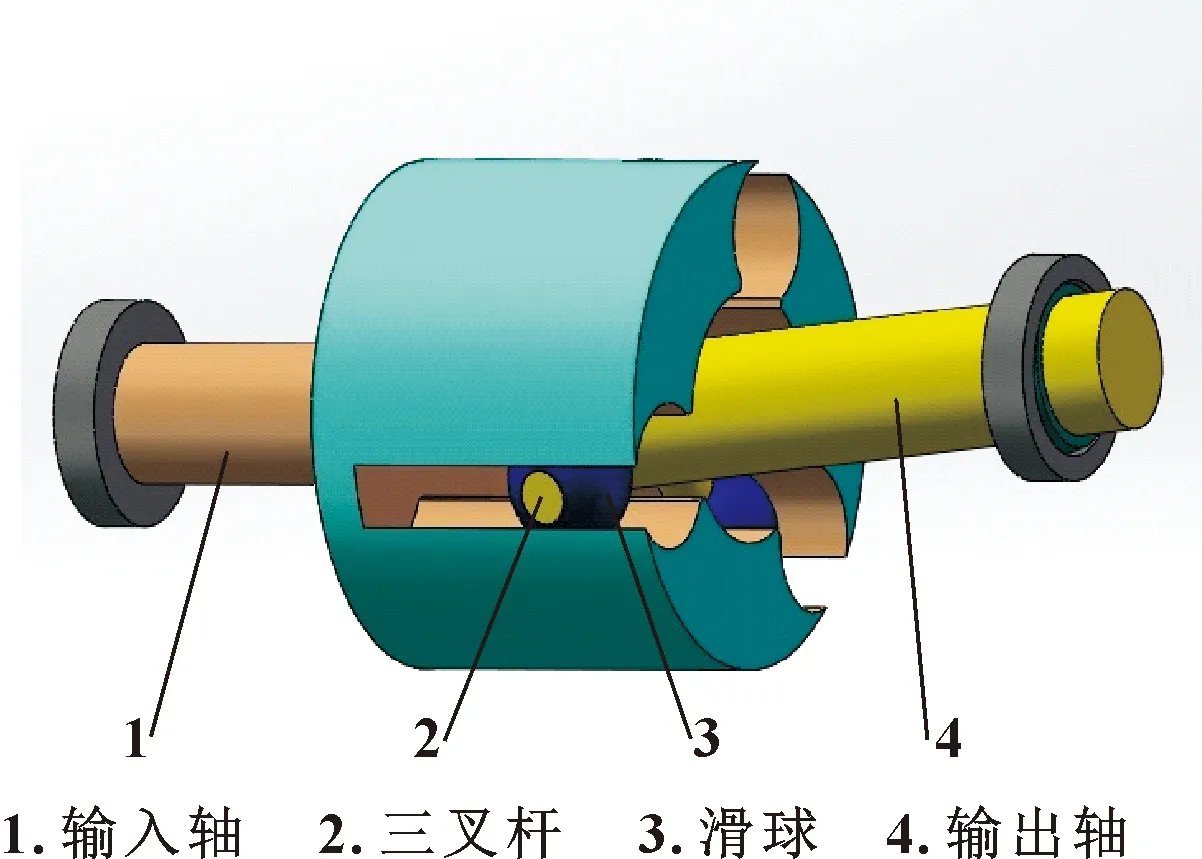
圖1 三叉桿滑球式萬(wàn)向聯(lián)軸器結(jié)構(gòu)

由于滑球與滑球滑道之間的幾何間隙沿滑球滑道是不變的，因此不容易形成有效的動(dòng)壓效應(yīng)，所以對(duì)三叉桿滑球式萬(wàn)向聯(lián)軸器的滑球重新設(shè)計(jì)。如圖2所示，文中在滑球上設(shè)計(jì)了一種多列相互平行的環(huán)形凸起新穎結(jié)構(gòu)，這種結(jié)構(gòu)可以形成局部先收斂后發(fā)散的接觸區(qū)域，更好地形成動(dòng)壓效應(yīng)和潤(rùn)滑油膜。根據(jù)滑球與滑球滑道的接觸部位特征，可以將滑球與滑球滑道的接觸部位當(dāng)作是線接觸。

圖2 滑球結(jié)構(gòu)

1.1.2 基本方程

假設(shè)潤(rùn)滑油為牛頓流體，則等溫線接觸彈流潤(rùn)滑Reynolds方程[17]如下

(1)

式中：x為卷吸速度方向標(biāo)量；p為油膜壓力，Pa；h為油膜厚度，m；η為潤(rùn)滑油黏度，Pa·s；ρ為潤(rùn)滑油密度，kg/m3；us為卷吸速度,m/s，潤(rùn)滑接觸面的平均速度us=(u+0)/2=u/2

Reynolds方程邊界條件設(shè)置為

p(x0,t)=0,p(xe,0)=0,p≥0(x0≤x≤xe)

膜厚方程為

(2)

式中：h0為剛體中心膜厚，m；R為等效曲率半徑，m；E′為兩接觸面的綜合彈性模量，Pa；s為x軸上的附加坐標(biāo)，為任意線載荷p(s)ds與坐標(biāo)原點(diǎn)的距離;p(s)是載荷分布函數(shù)；Ra(x)為表面粗糙度函數(shù)。

黏度-壓力方程為

η=η0exp{(lnη0+9.67)[(1+5.1×10-9p)z-1]}

(3)

式中：z=α/[5.1×10-9×(lnη0+9.67)]；η為潤(rùn)滑油黏度，η0為零壓時(shí)潤(rùn)滑油黏度；α為黏壓系數(shù)，Pa-1。

密度-壓力方程為

(4)

式中：ρ0為零壓時(shí)潤(rùn)滑油密度，kg/m3。

當(dāng)外載荷不變時(shí)，載荷方程為

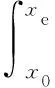
(5)

1.1.3 表面粗糙度

考慮三叉桿滑球式萬(wàn)向聯(lián)軸器的實(shí)際工作情況，采用隨機(jī)表面粗糙度更符合實(shí)際情況。為簡(jiǎn)便計(jì)算，可以采用將表面粗糙度當(dāng)成算數(shù)平均偏差Ra的2倍或輪廓的最大高度Rz，其中優(yōu)先采用Ra。由于計(jì)算過(guò)程中采用隨機(jī)數(shù)的方法可以簡(jiǎn)化計(jì)算[17]，則表面粗糙度函數(shù)Ra(x)簡(jiǎn)化為

Ra(x)=2×Ra×δ(x)

(6)

式中：Ra為粗糙度幅值;δ(x)為0～1之間的隨機(jī)數(shù)。

1.1.4 方程量綱一化

通過(guò)量綱一化后，等溫彈流潤(rùn)滑線接觸的Reynolds方程[18]為

(7)

式中：ε=ρH3/(ηλ)，λ=12η0UR2/(b2pH)，U為平均速度,R為等效曲率半徑,b為 Hertz接觸區(qū)半寬，b=[8wR/(πE′)]1/2；X=x/b，X為量綱一化坐標(biāo)；P=p/pH,P為量綱一化壓力，pH為最大 Hertz最大壓力；H=hR/b2，H為量綱一化膜厚，ρ*=ρ/ρ0；η*=η/η0。

其邊界條件為

量綱一化膜厚方程為

(8)

式中：H0為量綱一化剛體位移；X0和Xe分別為入口處和出口處量綱一化坐標(biāo)。

量綱一化密壓方程為

(9)

量綱一化黏壓方程為

η*=exp{(lnη0+9.67)[(1+5.1×10-9P)z-1]}

(10)

式中：z=α/[5.1×10-9×(lnη0+9.67)]。

量綱一化載荷方程為

(11)

1.2 數(shù)值計(jì)算方法

采用Newton-Raphson方法對(duì)方程進(jìn)行數(shù)值求解，計(jì)算出對(duì)應(yīng)矩陣變量的增量，并使用增量迭代計(jì)算法進(jìn)行計(jì)算。在計(jì)算過(guò)程中因?yàn)橐氡砻娲植诙龋捎跐?rùn)滑油膜膜厚的初始形狀比較粗糙，最后求得的理想表面的壓力值與實(shí)際情況的差距較為明顯，導(dǎo)致求解結(jié)果不易收斂[17]。因此在求較大的粗糙度值的解時(shí)，應(yīng)選取逐漸遞增表面粗糙度的幅度的方式來(lái)解決。當(dāng)粗糙度每次遞增后，該次的起始值就是在上一次的較小的粗糙度的結(jié)果中求解得到，從而使結(jié)果不容易發(fā)散。

由于油膜的彈性變形根據(jù)壓力的改變而發(fā)生改變，黏度也同樣如此。所以，為計(jì)算潤(rùn)滑油膜的厚度和所使用潤(rùn)滑油的黏度，通常先設(shè)定起始?jí)毫χ担春掌澖佑|壓力值，求出潤(rùn)滑油膜的厚度和潤(rùn)滑油的黏度后再代入雷諾方程中計(jì)算得到全新的壓力分布，迭代修正上一次求解得出的壓力分布，并且重新迭代求解油膜厚度和壓力值。重復(fù)迭代計(jì)算求解，直到計(jì)算出來(lái)的壓力差值滿足相對(duì)收斂精度判斷準(zhǔn)則，迭代計(jì)算結(jié)束，得到最終所需的油膜厚度和壓力分布[17]。

壓力的周期性相對(duì)收斂精度判斷準(zhǔn)則[17]為

(12)

式中：k+1表示目前所運(yùn)行的循環(huán);k表示上一次已經(jīng)結(jié)束的循環(huán)。當(dāng)超過(guò)4個(gè)循環(huán)并且滿足收斂準(zhǔn)則時(shí)，跳出循環(huán)，得到收斂解，計(jì)算結(jié)束。

計(jì)算流程如圖3所示。

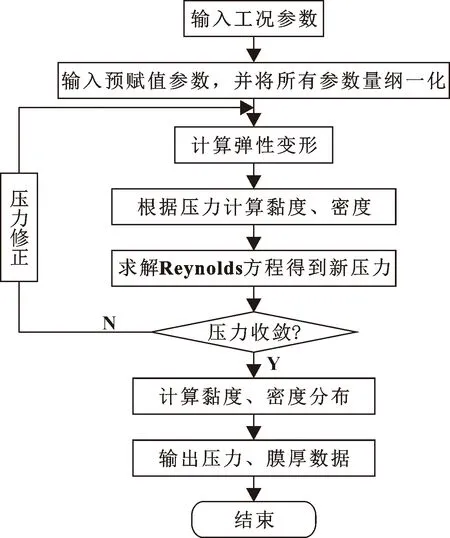
圖3 計(jì)算流程

2 計(jì)算結(jié)果及分析

計(jì)算時(shí)初始參數(shù)設(shè)置為：Xe=-X0=150，滑球半徑R=13 mm，載荷w=100 kN/m，轉(zhuǎn)動(dòng)頻率f=30 Hz，軸線夾角β=10°，潤(rùn)滑接觸面的平均速度為us=0.471 m/s，綜合彈性模量E′=2.27×1011Pa。潤(rùn)滑劑選擇P100潤(rùn)滑油，在溫度295 K下,η0=0.214 Pa·s，α=2.354×10-8Pa-1，ρ0=870 kg/m3。

2.1 表面粗糙度幅度的影響

其他條件不變，當(dāng)表面為理想表面和粗糙度幅度分別取0.01、0.03、0.05 μm的表面時(shí)， 對(duì)潤(rùn)滑油膜膜厚和壓力的影響如圖4和圖5所示。

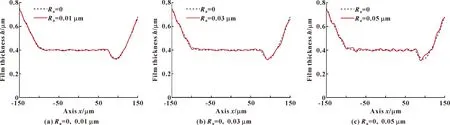
圖4 表面粗糙度幅度對(duì)膜厚的影響

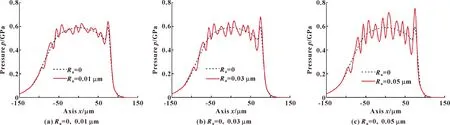
圖5 表面粗糙度幅度對(duì)壓力的影響

如圖4所示，從整體來(lái)看，相比理想表面，考慮表面粗糙度的表面油膜膜厚曲線存在波動(dòng)，并且隨著表面粗糙度幅度的增大，膜厚曲線從略微波動(dòng)到逐漸明顯的波動(dòng)，但是波動(dòng)沒(méi)有顯著的規(guī)律；接觸區(qū)域的中心油膜厚度隨表面粗糙度幅度的升高而變大。

由潤(rùn)滑理論得知，因?yàn)殡S機(jī)粗糙度改變膜厚的頻率是無(wú)序的，膜厚隨著表面粗糙度幅度的增大而增大，所以膜厚曲線的波動(dòng)是隨機(jī)粗糙度的無(wú)序頻率引起的，進(jìn)而導(dǎo)致了潤(rùn)滑性能的變化。在不考慮溫度變化的情況下，表面粗糙度較小時(shí)，表面粗糙度是影響潤(rùn)滑油膜厚度的主要因素，所以油膜厚度隨表面粗糙度幅度的增大而增大。但是當(dāng)潤(rùn)滑油膜厚度的增加值比表面粗糙度的增加值小時(shí)，即潤(rùn)滑油膜厚度相對(duì)于表面粗糙度減少了，這將導(dǎo)致滑球表面與滑球滑道表面的粗糙峰的接觸區(qū)域變大，從而造成潤(rùn)滑性能變差。

綜上所述，滑球與滑球滑道兩配合表面間的表面粗糙度幅度對(duì)于聯(lián)軸器的潤(rùn)滑性能影響較大，所以考慮表面粗糙度幅度對(duì)三叉桿滑球式萬(wàn)向聯(lián)軸器的摩擦潤(rùn)滑的研究至關(guān)重要。

如圖5所示，當(dāng)考慮表面粗糙度時(shí)，潤(rùn)滑油膜的壓力曲線產(chǎn)生了顯著波動(dòng)，曲線波動(dòng)范圍以理想表面壓力曲線為中心上下波動(dòng)，壓力波動(dòng)區(qū)域主要分布在中心部分，且局部壓力會(huì)很大；油膜的壓力波動(dòng)程度會(huì)隨著表面粗糙度幅值增大而加劇。

由潤(rùn)滑理論得知[14，17]，因?yàn)殡S機(jī)粗糙度改變膜厚的頻率是無(wú)序的，膜厚隨著表面粗糙度幅度的增大而增大。由于頻率的無(wú)序波動(dòng)，引起壓力曲線產(chǎn)生的波動(dòng)也是無(wú)序的，并且壓力值也隨著表面粗糙度幅值的增大而增大。所以壓力曲線波動(dòng)是隨機(jī)粗糙度的無(wú)序頻率引起的，進(jìn)而導(dǎo)致潤(rùn)滑性能的變化。

潤(rùn)滑油膜在滑球表面和滑球滑道表面之間形成，它們之間的表面由于隨機(jī)表面粗糙度幅度不一樣而產(chǎn)生高低不平，因此在這樣的表面之間會(huì)形成不一樣厚度的潤(rùn)滑油膜。此時(shí)的潤(rùn)滑油膜厚度相當(dāng)于原來(lái)的油膜厚度加上或減去隨機(jī)表面粗糙度幅度，并且從Reynolds方程中可以看出潤(rùn)滑油膜厚度與壓力之間存在關(guān)系，繼而使壓力曲線產(chǎn)生波動(dòng)，壓力值發(fā)生變化，而壓力又對(duì)初始油膜厚度有所影響，因此，隨機(jī)表面粗糙度的幅度對(duì)潤(rùn)滑油膜厚度產(chǎn)生重要影響，從而影響壓力。

2.2 表面粗糙度間距的影響

把表面粗糙度的間距縮小1/2，也就是把表面粗糙度輪廓單元的平均寬度縮小1/2，其他條件不變，當(dāng)表面為理想表面和粗糙度分別取0.01、0.03、0.05 μm的表面時(shí)，對(duì)潤(rùn)滑油膜膜厚和壓力的影響如圖6、7所示。

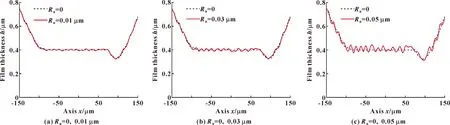
圖6 加密后表面粗糙度對(duì)膜厚的影響

圖7 加密后表面粗糙度對(duì)壓力的影響

如圖6、圖7所示，當(dāng)表面粗糙度間距縮小1/2后，考慮粗糙度的表面的潤(rùn)滑油膜厚度曲線和壓力曲線出現(xiàn)了波動(dòng)；并且與不改變表面粗糙度間距時(shí)相比，在波動(dòng)區(qū)域所產(chǎn)生的波動(dòng)程度更加密集，產(chǎn)生的潤(rùn)滑油膜厚和壓力的最大值會(huì)略微增大；另外隨著表面粗糙度的增大，波動(dòng)區(qū)域的波動(dòng)程度逐漸劇烈。

由潤(rùn)滑理論得知[14，17]，因?yàn)槟ず窈蛪毫η€的波動(dòng)是隨機(jī)粗糙度的無(wú)序頻率引起的，進(jìn)而引發(fā)了潤(rùn)滑性能的變化。當(dāng)表面粗糙度的間距縮小1/2時(shí)，相當(dāng)于在接觸區(qū)域內(nèi)的表面粗糙度改變膜厚和壓力的頻率加快，使膜厚和壓力發(fā)生改變，從而導(dǎo)致膜厚和壓力曲線的波動(dòng)密集且劇烈。

3 結(jié)論

(1)研究三叉桿滑球式萬(wàn)向聯(lián)軸器表面粗糙度幅度對(duì)膜厚和壓力的影響，結(jié)果表明，考慮粗糙度后表面的潤(rùn)滑油膜厚度曲線和壓力曲線相比理想表面存在波動(dòng)，并且隨著表面粗糙度幅度的增大，從略微波動(dòng)到波動(dòng)程度逐漸明顯。潤(rùn)滑油膜的壓力波動(dòng)區(qū)域主要分布在中心部分，且局部壓力會(huì)很大。

(2)研究表面粗糙度間距對(duì)膜厚和壓力的影響，結(jié)果表明，當(dāng)表面粗糙度間距縮小1/2時(shí)，考慮粗糙度后表面的潤(rùn)滑油膜厚度曲線和壓力曲線相比理想表面產(chǎn)生了波動(dòng)，并且與不改變表面粗糙度間距時(shí)相比，在波動(dòng)區(qū)域所產(chǎn)生的波動(dòng)程度更加密集，產(chǎn)生的潤(rùn)滑油膜厚度和壓力值的最大值會(huì)略微增大，并且隨著表面粗糙度的增大，波動(dòng)區(qū)域的波動(dòng)程度逐漸劇烈。