水壓馬達配流副橢圓形織構表面流場分析*

趙 濤 王優(yōu)強 胡 宇 何 彥 李夢杰 朱玉玲

(1.青島理工大學機械與汽車工程學院 山東青島 266520；2.工業(yè)流體節(jié)能與污染控制教育部重點實驗室 山東青島 266520)

進入21世紀，全球海洋事業(yè)迅速發(fā)展，海洋資源的開發(fā)利用成為了世界經濟增長的一大支柱。海水液壓馬達作為海洋探索的重要執(zhí)行元件有著極其重要的作用。然而，由于海水特殊的物理化學性質，海水液壓馬達中的關鍵摩擦副之一——端面配流副在海水中工作時極易因腐蝕、磨損而失效[1]。目前，國內外學者主要通過采用新材料[2-3]、改變潤滑方式[4-5]、進行涂層防護[6-7]等方法提高其摩擦學性能。隨著表面織構技術的發(fā)展，利用織構表面效應來進一步提高摩擦副的摩擦磨損性能有很大的潛力。

表面織構被認為是提高摩擦副表面摩擦學性能的有效方法之一。JONES和SCHMID[8]通過高頻率循環(huán)摩擦磨損實驗得到織構化表面的磨損性能明顯優(yōu)于光滑表面的結論。WAKUDA等[9]通過銷盤實驗模擬了具有很高接觸壓力的圓柱/平面接觸界面，研究發(fā)現(xiàn)織構化陶瓷摩擦副表面的摩擦特性與微坑大小和密度有很大關系，密度為5%～20%的微坑表面減摩效果最好。LIU等[10]通過數(shù)值模擬和實驗研究的方法，發(fā)現(xiàn)織構的幾何參數(shù)對摩擦副表面的摩擦學性能有顯著影響，最優(yōu)幾何參數(shù)取決于其所處的操作條件。袁明超[11]通過正交試驗分析了表面織構的不同參數(shù)對活塞環(huán)/缸套摩擦副摩擦學性能的影響，得出凹坑的直徑對摩擦副摩擦因數(shù)的影響最為顯著，當速度與載荷較高時，表面織構作用明顯。SAEIDI等[12-13]研究了不同工況下織構的不同參數(shù)對摩擦副摩擦學性能的影響，結果表明，織構直徑和面積率對摩擦因數(shù)的影響較大。GALDA等[14]研究了乏油條件下速度和載荷對織構化表面的影響，發(fā)現(xiàn)在低速低載條件下，織構的作用效果更明顯。

近年來，部分學者對海水液壓馬達關鍵部件進行摩擦學研究，探索織構化表面對其減摩抗磨性能的影響。梁瑛娜等[15-16]利用FLUENT仿真分析非光滑表面滑靴副的流體動壓支撐效應，并通過自制的試驗臺對加有織構的滑靴副進行了摩擦磨損測試，結果表明：織構能夠產生良好的動壓潤滑效應，織構的存在可以使?jié)櫥汉湍バ即鎯υ谄渲校档湍チＤp，加工有織構的摩擦副的摩擦因數(shù)和磨損率相較于光滑表面均大幅降低。孫怡龍等[17]利用ANSYS 軟件，分析了不同密度及不同深徑比凹坑對雙織構(上圓柱下圓錐)低速大扭矩水液壓馬達配流副等效摩擦應力的影響，發(fā)現(xiàn)織構化表面可以減小應力集中，有效降低摩擦副表面最大等效摩擦應力。WANG等[18]通過在CFRPEEK試樣上加工圓球形、橢球形和三棱柱型仿生織構，與光滑試樣進行摩擦磨損實驗對比，發(fā)現(xiàn)合適的非光滑表面能夠有效地降低摩擦副的摩擦因數(shù)，其中，橢球形織構的摩擦性能最好。馬浩等人[19-20]通過對比不同形狀的織構化配流副表面，發(fā)現(xiàn)圓形織構具有最好的流體動壓潤滑性能。但目前為止，很少有學者探究同一織構的不同參數(shù)對海水液壓馬達配流副潤滑性能的影響規(guī)律。

本文作者利用FLUENT軟件，在不同轉速、不同面積率下對不同直徑的橢圓形織構進行仿真分析，探究其影響規(guī)律，為加工織構化配流副表面提供理論依據(jù)。

1 仿真模型的建立

1.1 表面織構幾何模型及FLUENT模型選擇

文中根據(jù)WANG等[18]和YU等[21]的研究成果，選擇潤滑效果最好的垂直于滑動方向的橢圓形織構布置在配流副表面；同時為節(jié)省運算時間、提高精度，故選取配流副的一個具有表面織構的圓環(huán)單元進行計算，如圖1(a)所示，圓環(huán)單元尺寸如圖1(b)所示。

定義凹坑總面積與單元圓環(huán)總面積的比值為凹坑面積占有率A，則

式中：a、b分別為橢圓的短半軸長、長半軸長，mm；x為凹坑數(shù)量；R、r分別為圓環(huán)單元模型的外、內半徑，mm。

XU等[22]通過研究發(fā)現(xiàn)，長短軸比為2∶1的橢圓形織構能有效地減摩抗磨，而過大的長短軸比則會加劇磨損。故文中選取橢圓形織構的長短軸比為2∶1。文中設計3種不同尺寸的橢圓形織構，其長短軸分別是1.6、0.8 mm，1.2、0.6 mm和0.8、0.4 mm，在文中表示為1.6/0.8、1.2/0.6、0.8/0.4 mm；織構面積率分別是5%、8%、10%、13%、18%、21%；織構深度保持不變，為0.4 mm。

文中主要研究海水潤滑下織構化配流副表面的流體動壓效應，故采用不可壓縮流體、定常、湍流模型進行分析。湍流模型選用旋轉流動分析性能更好的Realizablek-ε模型。工作介質為海水，其密度為1 025 kg/m3，動力黏度為1.037×10-3Pa·s。

1.2 網格劃分及無關性驗證

網格質量的好壞會影響仿真分析結果，合適的網格能加快計算收斂速度，提高運算精度。文中利用ANSYS自帶的Mesh模塊對水膜單元模型進行四面體網格劃分，求解偏好為CFD Fluent，運用能夠較好捕捉曲率變化的Curvature法，關聯(lián)度采用Medium，跨度中心角設置為Fine。文中模型的網格質量系數(shù)的平均值約為0.75，偏斜系數(shù)的平均值約為0.27，配流盤水膜單元模型及網格劃分如圖2(a)、(b)所示。在保證計算精度同時，為減少計算時間，文中以1.2/0.8 mm的橢圓形織構水膜為例進行網格無關性驗證，如圖3所示。隨著單元總數(shù)的減小，水膜上表面最大壓力基本保持不變，網格質量隨單元總數(shù)的減小也基本趨于平緩。根據(jù)驗證結果，整個計算模型的單元總數(shù)取1 764 315個，即對應的網格尺寸為0.03 mm。

圖2 配流盤水膜模型及局部網格劃分

圖3 無關性驗證

1.3 邊界條件及計算參數(shù)的設置

邊界條件設置如圖4所示:與轉子相接觸的表面設置為動面，且沿主軸做逆時針勻速圓周運動，取主軸轉速分別為500、1 500、2 500 r/min；固定壁面設置為與配流副表面相接觸的表面，圓環(huán)內表面設置為壓力入口邊界，圓環(huán)外表面設置為壓力出口邊界，取進出口壓力均為0。采用 SIMPLEC 算法進行求解，壓力項選用Body Force Weighted，其余項均選用Second Order Upwind。

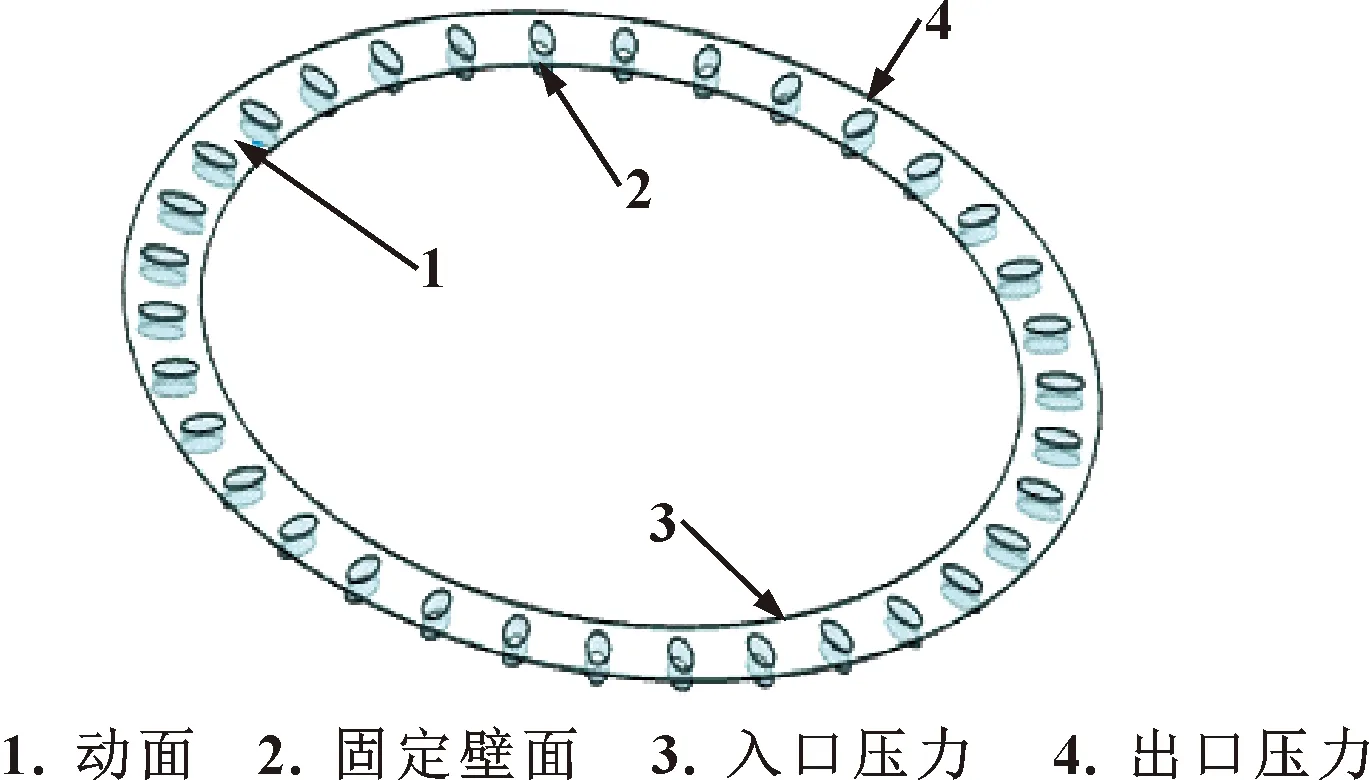
圖4 邊界條件

2 結果分析與討論

2.1 計算模型有效性驗證

為保證計算模型的有效性，設定模型幾何參數(shù)、控制方程、邊界條件及網格劃分方法與文獻[15]保持一致，但設定其工作條件與文中保持一致。如圖5所示為文中模型與文獻[15]中模型的壓力對比情況，文中壓力變化趨勢與文獻[15]中壓力變化趨勢基本一致，表明文中采用的計算模型和計算方法較為合理。

圖5 文中方法計算結果與文獻[15]結果對比

2.2 水膜上表面壓力分布

為探究橢圓形織構表面的水膜承載特性，取轉速為2 500 r/min，面積率為13%的3種不同尺寸的橢圓形織構進行了分析，其二維壓力云圖、三維壓力山峰圖如圖6所示。設定摩擦副繞軸線順時針旋轉，由圖6(a)、(c)、(e)可知，沿順時針方向，凹坑處的水膜壓力呈現(xiàn)出先減小后增大的現(xiàn)象，最小負壓出現(xiàn)在凹坑中心偏后位置，最大正壓出現(xiàn)在凹坑邊緣。結合三維壓力山峰圖，可以發(fā)現(xiàn)最大負壓均小于最大正壓，織構化水膜的整體壓力為正，即不同尺寸的橢圓形凹坑均能產生良好的水膜承載力。凹坑處水膜壓力先減小后增大的原因是加工在摩擦副表面的橢圓形織構在液體流動過程中會形成微小的收斂楔和發(fā)散楔[23]，水在流經凹坑時，凹坑的前緣會產生發(fā)散楔，導致水膜壓力下降，而水在流過凹坑時，凹坑后緣會形成收斂楔，水膜壓力急劇升高。

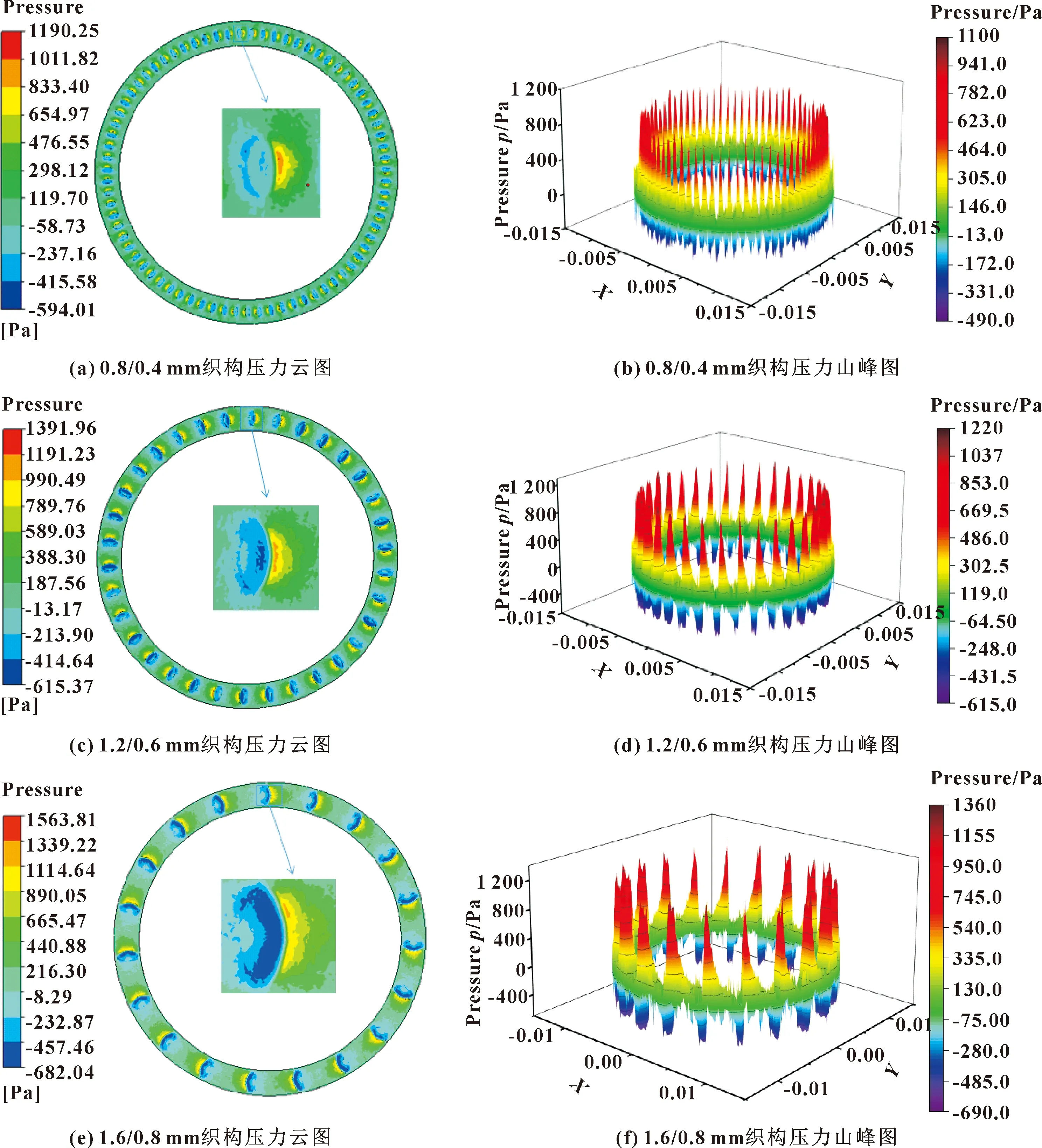
圖6 不同尺寸的橢圓形凹坑的壓力云圖和壓力山峰圖

2.3 面積率及轉速對不同尺寸橢圓形織構的影響

圖7所示為不同尺寸橢圓形織構在不同轉速下的平均水膜壓力隨面積率的變化情況。可知，在相同面積率下，3種不同尺寸織構的水膜壓力都隨轉速的增大而增大，這是因為水膜總壓由動壓和靜壓組成且由動壓主導[15]。動壓的表達式為ρv2/2。隨著轉速的不斷增大，動壓也隨之增大，從而導致總壓增大。對比3種不同尺寸織構的壓力曲線，相同尺寸的橢圓形織構在不同轉速下其水膜壓力隨面積率的變化呈現(xiàn)出相同的變化規(guī)律，并且，轉速越大，變化越顯著。另外，不同尺寸橢圓形織構的水膜壓力隨面積率的變化呈現(xiàn)出不同的變化規(guī)律。其中，尺寸為0.8/0.4、1.6/0.8 mm的橢圓形織構的水膜壓力隨面積率的變化總體呈現(xiàn)出先增大后減小的趨勢，其最優(yōu)面積率分別為13%和18%；而1.2/0.6 mm的橢圓形織構總體呈現(xiàn)出不斷增大的變化趨勢，其最優(yōu)面積率為21%。通過對比3種尺寸的橢圓形凹坑，可以發(fā)現(xiàn)隨著織構尺寸的不斷增大，橢圓形織構的最優(yōu)面積率的變化趨勢為先增大后減小。

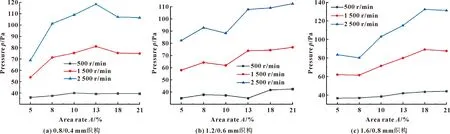
圖7 不同尺寸橢圓形織構在不同轉速下水膜壓力隨轉速的變化

針對以上變化規(guī)律，文中以直徑為0.8/0.4 mm的橢圓形織構為例，分析得到面積率為8%、13%和21%的織構化表面的單個凹坑內的流跡線和壓力曲線，如圖8所示。隨著面積率的增大，凹坑內已成核渦旋先向右上移動再回落，在凹坑面積率為13%時，渦旋離摩擦副上壁面最近，產生的流體動壓效應最強。通過對比壓力曲線圖，面積率為8%的凹坑在89°～90.5°的低壓區(qū)的壓力波動范圍較大，能量損失大，故其整體水膜支撐力最小；而面積率為13%和18%的凹坑在此范圍內的壓力集中在-200 Pa左右，但面積率為18%的凹坑水膜壓力波動較面積率為13%的凹坑的水膜壓力波動大；另外，面積率的增大導致織構間距不斷減小，當織構間距過小時，相鄰織構的發(fā)散楔和收斂楔相互影響顯著，即前一個凹坑的收斂區(qū)與后一個凹坑的發(fā)散區(qū)部分抵消[24]，故而，面積率為18%的織構表面凹坑內的高壓區(qū)不及面積率為13%的織構表面。綜上所述，面積率為13%的織構表面整體水膜支撐力最大，面積率為18%的織構次之。

由以上分析可知，直徑為0.8/0.4、1.2/0.6和1.6/0.8 mm的橢圓形織構的最優(yōu)面積率分別是13%、21%和18%，在此基礎上，文中進一步探究不同直徑的橢圓形織構在各自最優(yōu)面積率下的最大水膜壓力隨轉速的變化，如圖9所示。3種不同直徑橢圓形織構的水膜壓力都隨轉速的增大而增大，其中直徑為1.6/0.8 mm的橢圓形織構表面水膜壓力最高，直徑為1.2/0.6 mm的橢圓形織構表面水膜壓力次之；直徑為0.8/0.4 mm的橢圓形織構表面水膜壓力最低。

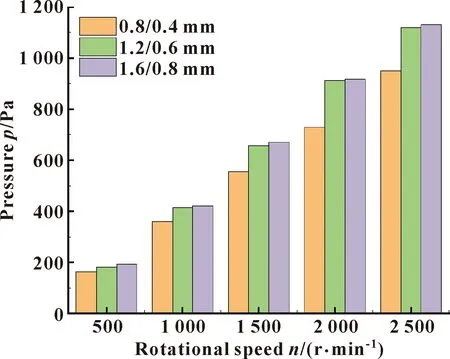
圖9 不同尺寸織構表面最大水膜壓力隨轉速的變化

圖10所示為2 000 r/min下不同直徑橢圓形凹坑的流跡線和速度梯度。對比圖10(a)、 (c)和(e)，可以發(fā)現(xiàn)凹坑的右上角存在一個成形的渦旋，隨著凹坑直徑的不斷增大，成形渦旋不斷向收斂楔方向移動；而在凹坑的左下角逐漸形成一個小渦旋。結合圖10(b)、(d)和(f)，隨著凹坑直徑的增大，右上角的渦旋體積不斷減小，流體動能轉換成漩渦能量的效應減弱，水膜壓力上升，且凹坑的左下角在渦旋形成的過程中，速度梯度變化更加緊密，流體動壓效應愈加明顯；另外，凹坑尺寸的增大使撞擊凹坑底部的水流束更加集中，產生更大的回流沖擊效應。通過以上各點的綜合作用，使得在一定范圍內，凹坑尺寸越大，水膜壓力越高。

圖10 2 000 r/min下不同直徑凹坑的流跡線和速度梯度

3 結論

建立橢圓形織構液壓馬達配流副表面模型，分析織構參數(shù)對水膜承載性能的影響，仿真結果表明：

(1)不同尺寸的橢圓形織構均能產生良好的水膜承載力，其水膜承載力隨面積率的變化呈現(xiàn)出不同的變化規(guī)律，但相同尺寸的橢圓形織構隨面積率的變化呈現(xiàn)出相同的變化規(guī)律，在實際應用中應根據(jù)不同的織構尺寸選擇不同的面積率。

(2)在相同面積率下，轉速越高，織構的水膜承載力越強，故在高轉速配流副中，織構能夠產生更好的承載效果。

(3)通過對比不同尺寸的橢圓形織構在各自最優(yōu)面積率下對水膜承載力的影響，無論在多大轉速下，1.6/0.8 mm的橢圓形織構能表現(xiàn)出較優(yōu)的水膜承載性能。