基于隨機森林算法的改性水潤滑軸承摩擦性能預測*

王 裕 徐起秀 郭智威 袁成清

(武漢理工大學，國家水運安全工程技術研究中心，可靠性工程研究所 湖北武漢 430063)

船舶尾軸承是船舶軸系中用于支撐螺旋槳軸的關鍵部件[1]。隨著綠色航運的發(fā)展，水潤滑軸承已逐步替代油潤滑軸承。但水潤滑軸承使用水作為潤滑介質，由于水的黏度低，對材料的摩擦磨損性能提出更高的要求，因而提高水潤滑尾軸承在船舶使用過程中的摩擦磨損性能已成為研究重點[2]。

針對船舶尾軸承的相關實驗研究很多，已累積了大量數(shù)據(jù)。以水潤滑尾軸承為例，目前已建立其相關摩擦性能數(shù)據(jù)集。因此，基于大數(shù)據(jù)理論，通過對原數(shù)據(jù)集進行算法建模，尋找數(shù)據(jù)間的關聯(lián)性，對于預測水潤滑尾軸承在不同工況條件下的摩擦性能，指導水潤滑尾軸承的開發(fā)具有重要意義。

隨機森林算法[3]是一種集成學習算法，該算法是在決策樹算法基礎之上進一步優(yōu)化的一種算法模型，其原理是以原始數(shù)據(jù)為模型的訓練集，進行算法的創(chuàng)建，然后再通過創(chuàng)建的算法模型預測數(shù)據(jù)的變化趨勢。隨著隨機森林算法的參數(shù)的不斷優(yōu)化，其性能也更加準確，可以較為精確地模擬數(shù)據(jù)中存在的未知關系并用于預測未知數(shù)據(jù)或者趨勢，通過構建隨機森林學習算法模型可以用來實現(xiàn)數(shù)據(jù)的分類或者預測回歸[4]。

本文作者運用隨機森林算法挖掘水潤滑尾軸承大量實驗數(shù)據(jù)中的隱藏信息，建立一種多模型思維的隨機森林算法，可準確地預測改性水潤滑尾軸承的摩擦磨損性能。

1 改性水潤滑軸承摩擦性能參數(shù)處理

水潤滑尾軸承的摩擦磨損性能對保障船舶的航行安全具有重要作用。本文作者所在的課題組，已針對該改性水潤滑軸承的摩擦磨損性能做了相關的實驗對比，獲得了相關的初始實驗數(shù)據(jù)。文中首先基于原始數(shù)據(jù)集進行建模前的數(shù)據(jù)預處理。

1.1 材料組成

文中研究的改性水潤滑尾軸承為質量分數(shù)10%聚乙烯蠟改性聚氨酯軸承，該軸承由聚乙烯蠟與聚氨酯聚合而成。首先將聚氨酯加熱至90 ℃，投入聚乙烯蠟后加熱至120 ℃共混，在共混過程中加入消泡劑(M-CDEA)，然后加熱至110 ℃，最后定性，得到如圖1所示的實驗樣品。文中將其命名為PU- PEW10[5]。

圖1 PU- PEW10試樣

1.2 數(shù)據(jù)處理

在PU- PEW10試樣摩擦磨損實驗的數(shù)據(jù)集中，原始數(shù)據(jù)集的特征屬性分別為溫度、壓力、扭矩、轉速、功率，以及經過實驗得出的摩擦因數(shù)。溫度控制由型號為HH-21-4的恒溫水箱控制。考慮到試樣磨合期數(shù)據(jù)存在波動，用于建模的原始數(shù)據(jù)取試樣磨合期后的穩(wěn)定實驗數(shù)據(jù)；考慮到恒溫水箱控制水溫時溫度會有一定的波動，文中針對溫度特征采用正態(tài)分布方法，補足數(shù)據(jù)集。HUANG等[5]的研究表明，在摩擦磨損實驗過程中，影響PU- PEW10試樣摩擦因數(shù)的外部因素主要為溫度、壓力和轉速。因此將對數(shù)據(jù)集整理后，得到如表1所示的可用于隨機森林算法建模的原始數(shù)據(jù)。

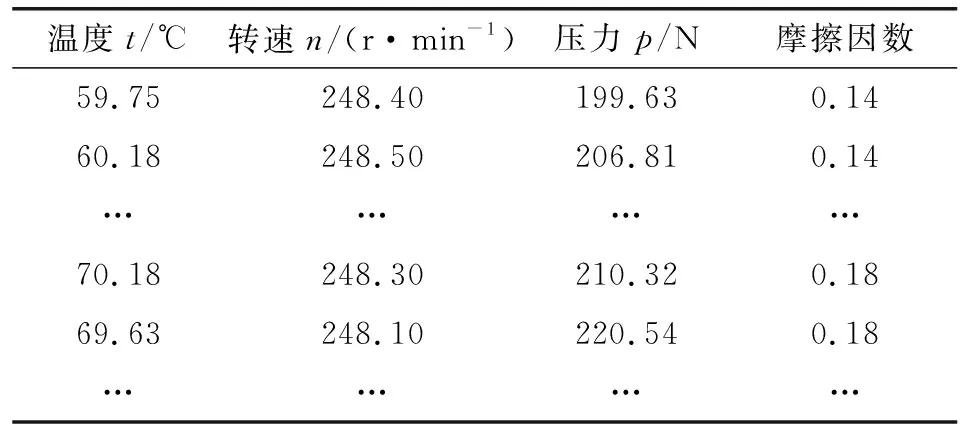
表1 處理后的影響因素數(shù)據(jù)和摩擦因數(shù)結果集

表1所展示的是將已知的5種工況下的數(shù)據(jù)整合成的一組數(shù)據(jù)。其中，5種工況參數(shù)分別為60 ℃、0.3 MPa，70 ℃、0.3 MPa，80 ℃、0.3 MPa，80 ℃、0.5 MPa以及60 ℃、0.7 MPa。溫度、轉速以及壓力都是隨機森林算法模型的特征屬性，即輸入值，摩擦因數(shù)是模型的輸出值。

2 隨機森林模型構建

隨機森林算法是一種集成學習算法，該算法是基于決策樹算法基礎上集合而成的一種多模型分類算法，因此文中先介紹決策樹算法原理。

2.1 決策樹算法原理

決策樹是一種最基本的模型分類回歸算法，是針對不同結果集進行分類的樹形結構算法。該算法通常包括3個學習步驟，分別為基于特征的選擇、決策樹的生成以及將構建的決策樹通過數(shù)據(jù)集進行剪枝操作。決策樹算法主要使用ID3算法、C4.5算法以及CART算法。決策樹由節(jié)點和有向邊組成，節(jié)點有2種類型：內部節(jié)點和葉節(jié)點。內部節(jié)點代表一個特征或一個屬性，葉節(jié)點表示一個類[6]。文中的隨機森林算法采用的是決策樹算法中的CART原理建模[7]，原理如下：

給定一個訓練集(文中的數(shù)據(jù)集為表1中的數(shù)據(jù))

D={(x1,y1),(x2,y2),…,(xn,yn)}

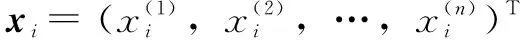
決策樹學習是根據(jù)給定的訓練數(shù)據(jù)集構建一個決策樹模型，使它能夠對實驗實例進行正確地分類。

文中使用的決策樹CART原理，是基于“基尼指數(shù)(Gini)”來選擇劃分特征屬性[8]。基于CART原理的決策樹模型用基尼系數(shù)最小化準則來進行特征選擇，生成二叉樹。數(shù)據(jù)集D的純度可用基尼系數(shù)來度量：

(1)

(2)

ΔGini(A)=Gini(D)-GiniA(D)

(3)

公式(3)用于計算基尼系數(shù)的增益，針對回歸問題應用最小平均誤差準則來檢驗模型的優(yōu)劣。文中構建模型的數(shù)據(jù)為經過預處理的摩擦因數(shù)數(shù)據(jù)集，將處理后的數(shù)據(jù)應用Python編寫決策樹算法模型，直接訓練數(shù)據(jù)集，得到訓練好的模型并對其進行準確性驗證，即計算該模型的均方根誤差(MSE)，發(fā)現(xiàn)該值為0.0，說明該模型可精確預測每一組摩擦因數(shù)值。但根據(jù)算法模型應用可知，當模型預測的MSE達到0.0時，表示模型能夠精準預測每一組數(shù)值，這種現(xiàn)象稱為“過擬合現(xiàn)象”，在該情況下需要對原模型進行超參數(shù)的調整，使其泛化能力更好。

調整超參數(shù)的方法有很多，文中采用網(wǎng)格搜索的方法確定模型的超參數(shù)數(shù)值，即包括樹的深度、節(jié)點數(shù)目等。網(wǎng)格搜索設置的參數(shù)為′max_depth′=[2, 3, 4, 5, 6, 7, 8, 9, 10]， ′min_samples_split′=[4, 8, 12, 16, 20, 24, 28]。′max_depth′指定了決策樹下鉆的深度，′min_samples_split′指定了分裂一個內部節(jié)點(非葉子節(jié)點)需要的最小樣本數(shù)。

決策樹構建完成后，需對優(yōu)化后的模型進行驗證。文中采用偏差方差法對優(yōu)化后的模型進行準確性驗證，通過算法自行計算，其MSE值為0.143，偏差(Bias)的值為0.055，方差(Variance)的值為0.088。可見，通過調整超參數(shù)′max_depth′以及′min_samples_split′的數(shù)值，使得模型有了一定的改進。但是一棵決策樹并不能很好地說明預測的準確性，最佳的處理方法是應用多棵決策樹進行預測值投票，得到最佳的預測結果，此時需要引進隨機森林算法來實現(xiàn)。

2.2 隨機森林算法

隨機森林算法是決策樹的集成，是以決策樹為基學習器基礎上構建bagging的方法，該方法在訓練數(shù)據(jù)時，通過每棵決策樹的CART方法，對數(shù)據(jù)中特征屬性隨機選擇最優(yōu)作為分類的基礎。采樣時，通過有放回的方法，構建多棵決策樹，每棵決策樹基于一定的精度進行分類。在此基礎上，每一棵樹再對預測或者分類的結果進行投票篩選，使得分類或預測的結果精度提高。

文中的隨機森林算法相對每個決策樹設置有同一個根節(jié)點，該節(jié)點的選擇由隨機森林算法隨機選取。從該節(jié)點中隨機選擇一個包含m個特征屬性的子集，再通過篩選的子集擇優(yōu)選擇一個特征屬性用來劃分，直到獲得最優(yōu)深度及節(jié)點數(shù)。其中m的含義為控制模型隨機性[9]的程度：當m與特征屬性數(shù)量相同時，那么構建的基決策樹與直接應用決策樹建模一致；如果m取1，則是通過算法選擇一個特征屬性來劃分；通常使用推薦值，即取m為log2d，其中d為特征屬性數(shù)量[6]。文中的特征屬性數(shù)量有3個，所以d取3，m取log23。

與決策樹算法一樣，將處理后的數(shù)據(jù)集直接用于隨機森林算法構建模型，模擬數(shù)據(jù)后計算該初始模型的MSE值，得出結果為0.027。鑒于數(shù)據(jù)量較少，文中采用了K折交叉驗證的方法，將數(shù)據(jù)重新進行構建模型。交叉驗證的方法是一種常用的模型選擇方法，該方法的提出是為了解決數(shù)據(jù)不充足問題，其基本思想為重復使用原始數(shù)據(jù)集。K折交叉驗證[10]是應用最多的一種交叉驗證方法，文中K取值為5，為一個較為適中的參數(shù)。

交叉驗證方法的原理[11]如下：將處理后的數(shù)據(jù)集進行數(shù)據(jù)切分，切分的原則是隨機性，保證數(shù)據(jù)的可信度；將切分后的數(shù)據(jù)集按照一定比例(文中按照8∶2的比例)分為訓練集與測試集，對數(shù)據(jù)集進行訓練并優(yōu)化。通過交叉驗證方法得到的不同訓練模型并用于投票選擇，然后通過測試集對每個模型進行誤差計算，并最終選出誤差最小的模型。

以K=5為例，K折交叉驗證的過程是：將處理后的數(shù)據(jù)集切分成5份互不相交、大小一致的數(shù)據(jù)子集；隨機選取其中的4份數(shù)據(jù)子集訓練模型，利用剩下的1份數(shù)據(jù)子集作為測試集驗證模型；每進行一次交叉驗證就將原始數(shù)據(jù)打亂并重新按照8∶2的比例將數(shù)據(jù)重新選擇并拆分為5份；將上述過程執(zhí)行5次，最終算法會選取其中平均測試誤差最小的模型用于改性水潤滑聚氨酯材料摩擦性能的預測。

基于上述方法，計算了優(yōu)化后模型MSE，其值為0.189。MSE值偏大，為此再將模型進行網(wǎng)格搜索[12]尋找隨機森林模型的最佳參數(shù)。首先嘗試12種(3×4)超參數(shù)組合，分別為′n_estimators′= [3, 10, 30]， ′max_features′=[2, 4, 6, 8]。其中n_estimators為隨機森林決策樹的數(shù)目，max_features為用來控制特征子集的數(shù)量，其值越小，隨機森林算法中的樹形結構差異越大，文中默認使用bootstrap重采樣方法，即有放回的可重復的抽取樣本；然后嘗試6種(2×3)boosting方法進行網(wǎng)格搜索最優(yōu)參數(shù)，即不放回的進行樣本建模，參數(shù)設置為′bootstrap′=[False]， ′n_estimators′=[3, 10]， ′max_features′=[1, 2, 3]，之后通過算法尋找最優(yōu)的參數(shù)組合。將′bootstrap′設置為True，即將數(shù)據(jù)集有放回的可重復的進行建模；′max_features′= 2，′n_estimators′= 30，即選取特征子集中的2個特征屬性組合，建立30棵樹模型。計算得到優(yōu)化后的模型的MSE值為0.178，可見優(yōu)化后的模型較之前的模型有了更好的泛化能力。

因為數(shù)據(jù)集中有5種分類狀況，為了評估每一類的預測情況，文中又對原始數(shù)據(jù)集做了分類算法，然后針對該模型計算每一類的接受者操作特征(ROC)曲線值，結果如圖2所示[11]。

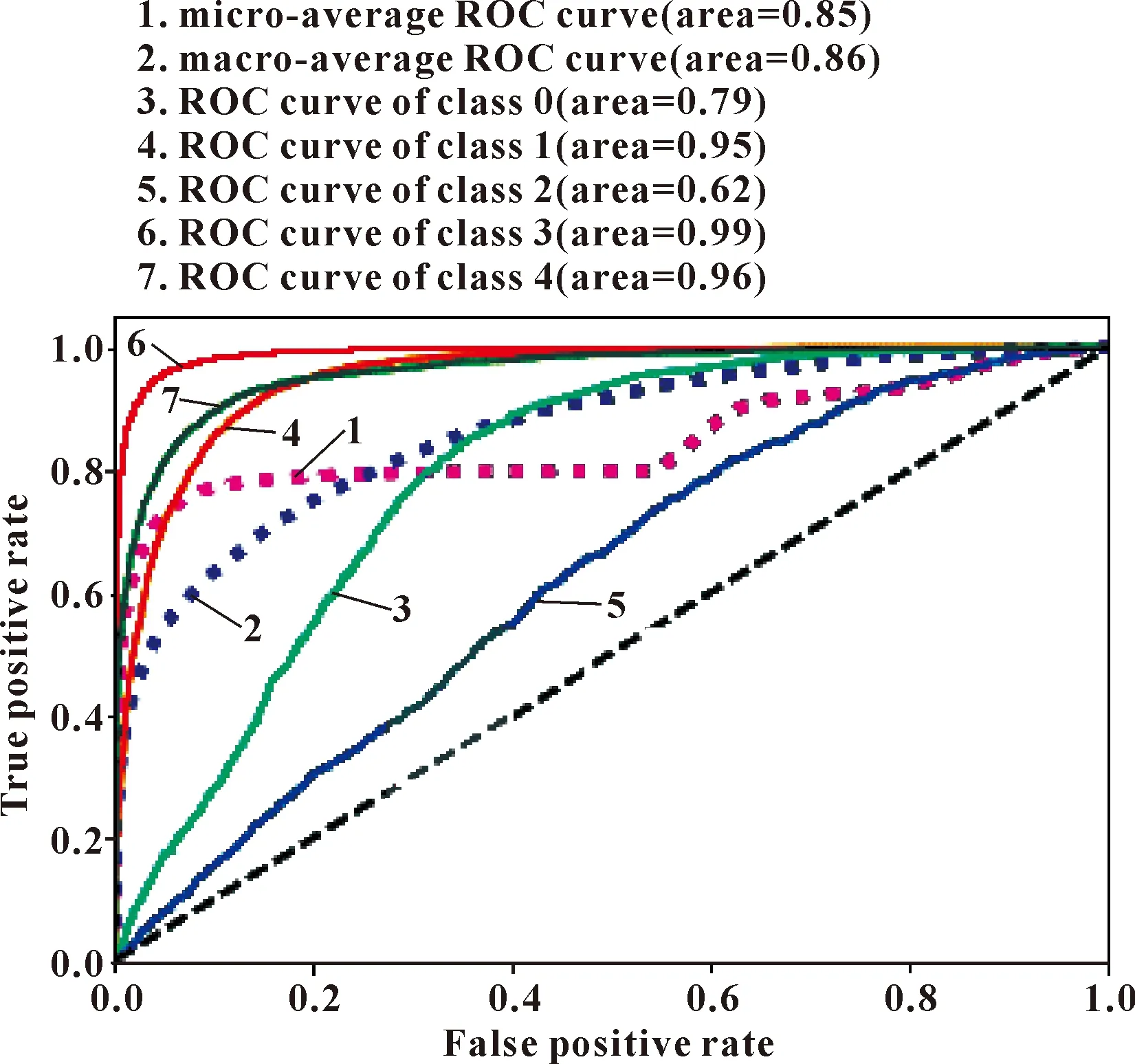
圖2 改性水潤滑軸承摩擦因數(shù)預測的ROC曲線

如圖2所示，其中class0—class4分別對應上述的5種不同工況，發(fā)現(xiàn)class0類與class2類的面積較低，即得分較低。但是micro-average ROC curve與macro-average ROC curve的平均值分別為0.85與0.86，從整體來看，該算法調整參數(shù)優(yōu)化后的模型分類較為準確，沒有出現(xiàn)過擬合或者欠擬合的狀態(tài)。所以優(yōu)化后的模型能夠較準確地預測出并分類改性水潤滑軸承的摩擦學性能。

2.3 模型結果

將所建的模型的均方根誤差(MSE)值進行對比，優(yōu)化前后其值分別為0.03以及0.178。優(yōu)化前MSE值不足0.1，即在預測每一個工況時均能夠準確預測摩擦因數(shù)，這種現(xiàn)象屬于過擬合現(xiàn)象[13]，模型不能完全準確地預測水潤滑軸承的摩擦性能。所以，優(yōu)化后的模型比優(yōu)化前的模型擁有更好的泛化性能[14]。隨機森林算法相較于決策樹算法，屬于一種多模型的算法，從上述分析得知，隨機森林是將數(shù)據(jù)集劃分成多棵樹來建立模型的一種集成算法，文中通過構建30棵決策樹，然后對其優(yōu)化并擇優(yōu)選擇最佳的模型，構建一種較為準確的隨機森林算法模型。

圖3所示為優(yōu)化后模型預測的不同工況下的摩擦因數(shù)。

圖3 隨機森林算法預測的不同工況下的摩擦因數(shù)

圖3中，T65N3、T75N3、T75N4、T75N5以及T85N3代表5種不同的工況，分別為65 ℃、0.3 MPa，75 ℃、0.3 MPa，75 ℃、0.4 MPa，75 ℃、0.5 MPa以及85 ℃、0.3 MPa，對應的摩擦因數(shù)預測值分別為0.18、0.20、0.20、0.18、0.18。

3 實驗驗證

3.1 摩擦因數(shù)實驗結果

采用表2所示實驗條件，通過實驗測量了該改性水潤滑軸承的摩擦因數(shù)及磨損量。

表2 實驗條件

考慮到實驗過程中改性水潤滑尾軸承和摩擦件之間有一個磨合階段，所以不同工況下材料的摩擦因數(shù)取磨合之后數(shù)據(jù)的平均值。圖4所示為0.3 MPa下改性水潤滑軸承不同溫度下的平均摩擦因數(shù)。根據(jù)HUANG等[5]的研究結果，在60～80 ℃之間該種材料的摩擦因數(shù)不斷增加，但是80 ℃后摩擦因數(shù)增加幅度開始下降。而文中實驗在文獻[5]的基礎上將溫度最大范圍增加5 ℃，達到85 ℃的工況，實驗發(fā)現(xiàn)，該材料的平均摩擦因數(shù)出現(xiàn)了下降的趨勢，表明該材料在80～85 ℃之間可能取得負載0.3 MPa工況下的最大平均摩擦因數(shù)。

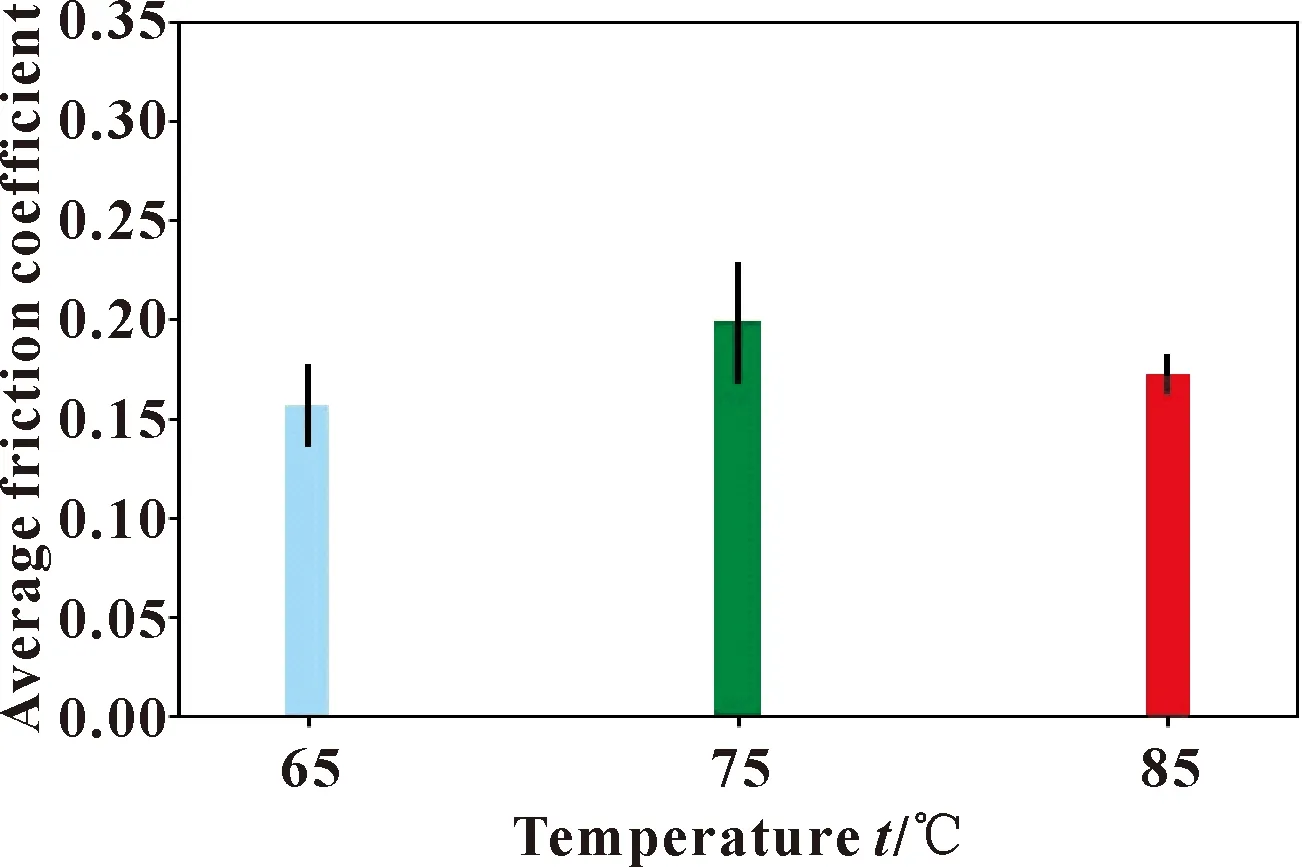
圖4 0.3 MPa下改性水潤滑軸承不同溫度下的平均摩擦因數(shù)

實驗過程中測得的材料在0.3 MPa載荷及65、75和85 ℃下的摩擦因數(shù)變化曲線如圖5所示。可得出，在相同的負載條件下，高介質溫度對于該材料摩擦因數(shù)的穩(wěn)定性和機械性能都產生了負面的影響[15-16]，其摩擦穩(wěn)定后的摩擦因數(shù)值均在0.15以上，說明高溫對于該材料的摩擦性能影響較大。

圖5 0.3 MPa及不同水潤滑溫度下的實時摩擦因數(shù)

圖6所示為75 ℃溫度及載荷0.3、0.4、0.5 MPa下的實時摩擦因數(shù)。在相同的水潤滑溫度條件下，隨著壓力增加，該材料的摩擦因數(shù)呈略微下降的趨勢，且壓力越大，摩擦因數(shù)越穩(wěn)定。產生這種現(xiàn)象的原因可能是，隨著壓力的增加，改性水潤滑聚氨酯與摩擦件之間接觸面變大，貼合效果也越好[17]。通過圖6也可以看出，在研究的載荷范圍內，載荷的大小對于該材料摩擦因數(shù)的數(shù)值影響不大，但是對其穩(wěn)定性影響較大。

圖6 75 ℃及不同壓力下的實時摩擦因數(shù)

3.2 仿真與實驗結果對比

表3給出了實驗和仿真得到的該改性水潤滑軸承在不同工況下的摩擦因數(shù)及誤差率。可見實驗值和仿真值誤差率均在5%左右。考慮到在實驗過程中產生的振動等因素導致壓力不穩(wěn)的情況，會導致實驗結果和預測結果有一定的偏差，但兩者的偏差較小，所以可認為預測結果較為準確。

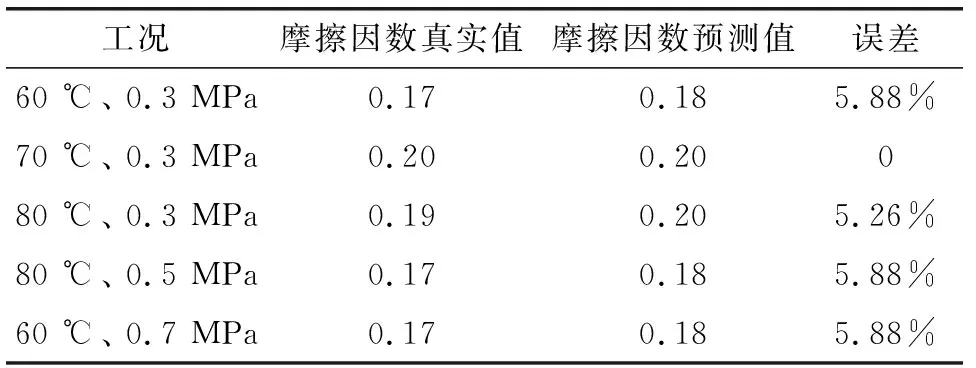
表3 不同工況下摩擦因數(shù)真實值與預測值對比

比較隨機森林算法預測的摩擦因數(shù)值與實驗得出的結果，可以發(fā)現(xiàn)：溫度對于該改性水潤滑軸承的平均摩擦因數(shù)有較大的影響，在75～85 ℃之間會產生一個峰值，此時該改性水潤滑軸承的磨損會增加；負載對于該材料的平均摩擦因數(shù)的影響較小，但是對于軸承的運轉穩(wěn)定性影響較大。

4 結論及展望

(1)基于大量實驗數(shù)據(jù)，建立了一種多模型思維的隨機森林算法，作為一種基于決策樹的集成算法，提高了計算精度。

(2)引入ROC曲線，基于構建的模型分類器進行了準確度評價，進一步證明了算法的準確性。隨機森林算法引入了隨機性的概念，使得模型不容易過擬合，模型的訓練速度快，較為準確地預測了改性水潤滑尾軸承的相關摩擦性能數(shù)據(jù)。

(3)比較隨機森林算法預測結果與實驗結果可以得出：溫度對于該改性水潤滑軸承的平均摩擦因數(shù)有較大的影響，在75～85 ℃之間會產生一個峰值，此時該改性水潤滑軸承的磨損會增加；負載對于該材料的平均摩擦因數(shù)的影響較小，但是對于軸承的運轉穩(wěn)定性影響較大。

(4)文中研究尚有不足之處，即在進行摩擦性能預測時，只針對一種特定的改性水潤滑軸承進行了預測，下一步研究將會針對不同的改性水潤滑軸承的摩擦性能進行預測，使算法預測更具有普適性。