基于分形接觸理論的機械密封泄漏率與膜厚預測*

趙玉霞 丁雪興 王世鵬

(蘭州理工大學石油化工學院 甘肅蘭州 730050)

隨著旋轉類透平機械軸端密封的不斷發展，機械密封在服役過程中，密封性能會隨端面摩擦接觸發生變化[1-2]。端面參數的變化會使得機械密封泄漏率和平均膜厚發生改變[3]。機械密封的磨損加劇時，密封端面的摩擦性能逐漸變差，使得其泄漏率超標，會造成密封嚴重的泄漏損失。因此，如何結合密封端面性能參數，對泄漏率和平均膜厚進行有效預測，是機械密封性能研究的關鍵性問題。

近年來，國內外學者對于機械密封端面參數對密封特性和泄漏率影響的研究，已經取得一定成果。MAYER[4]通過平行端面泄漏模型對平面縫隙的泄漏率進行計算，發現試驗與理論值存在偏差，表明摩擦狀態接觸壓力會影響密封的磨損性能。LEBECK[5-6]通過考慮機械密封的摩擦狀態，建立混合狀態下泄漏率計算模型，并得出彈性接觸為粗糙表面接觸的主要形式。GREEN[7]通過研究端面微凸體接觸磨損對端面錐角產生的影響，提出了和時間相關的泄漏通道模型，得出當臨界速度較高時，氣體黏性較低以及加熱效應較小，接觸端面主要為干摩擦狀態。MECK和ZHU[8-9]利用有限元分析和計算流體力學CFD集成了流體膜和摩擦學模型，以此預測機械密封的性能，通過試驗驗證發現界面潤滑條件的改善，會使密封面摩擦減少。KEY、SALANT等[10-11]提出密封泄漏模型，并通過有限差分法計算了槽型對泄漏率的影響，驗證了轉速低于臨界值時，泄漏率將超過相同油膜厚度的等效平面密封。DAPP等[12]通過對密封泄漏通道中流體流動的數值仿真，研究了密封面彈性固體間具有隨機粗糙及自仿射表面的流體流動，可以得到密封面泄漏通道的流體速度分布以及密封面總泄漏量。ZAHORULKO和LEE[13]采用穩態CFD和實驗設計方法，分析了鐮刀槽扇形密封泄漏率與其幾何參數的關系，發現泄漏率的增加更可能是由于周向流速的降低而不是軸向流速的增加。隨后越來越多學者致力于粗糙表面對密封性能的影響研究。丁雪興等[14-15]通過迭代法、PH線性化方法求解二階非線性雷諾方程，以此得到氣膜壓力、流速和泄漏量的近似解；同時結合分形接觸模型與塑性變形機制，建立了與分形參數相關的磨損率模型，研究表明磨損率隨接觸面積增大而增大。彭旭東、楊笑等人[16-17]對機械密封端面粗糙度、錐度及流體性能進行研究并提出徑向泄漏模型，發現隨著粗糙度增加，泄漏量和膜厚會增加；同時基于空化理論建立了機械密封混合潤滑計算模型，得到機械密封粗糙表面性能優于光滑表面性能的結論。孫見君等[18-19]根據分形幾何理論，建立了機械密封接觸剛度分形模型和密封泄漏模型，驗證了密封運轉過程中存在使泄漏最小的端面參數。魏龍等人[20-22]根據平均膜厚分形模型，結合壓力流量因子，建立了機械密封泄漏分形模型，得出了泄漏率與端面參數的關系。李小彭等[23]通過對機械密封動靜環間的接觸進行簡化，建立了解析泄漏模型，證明機械密封泄漏率Q與端面分形維數D成反比，而與尺度系數G成正比。陳志等人[24]對干摩擦時機械密封端面接觸特性進行研究，建立轉動摩擦熱-力耦合模型，得出隨外載荷的增大機械密封粗糙端面的真實接觸面積近似線性增加。當前，對機械密封的微凸體面積泄漏率的計算研究存在偏差并且鮮有文獻發表。

為了更近一步提高機械密封泄漏率計算的精確度，本文作者將分形泄漏率模型與分形接觸模型相結合，并根據泄漏率等效原則，建立了基于分形接觸理論的平均膜厚預測模型；此外對不同端面分形參數、工況條件、材料特性系數下的泄漏率與平均膜厚進行了分析討論，為今后進一步研究機械密封的摩擦與潤滑提供一定的支撐。

1 理論模型

機械密封動環與靜環一般采用一硬一軟2種材料進行配副，因此，在機械密封端面研究中，將機械密封的硬質環簡化為剛性理想光滑平面，將軟質環簡化為粗糙表面。此外，在模型建立時做出如下假設：

(1)機械密封端面間的流體流動為不可壓縮黏性流體的層流流動；

(2)密封端面為平行端面，其接觸視為粗糙表面與光滑平面之間微凸體接觸，微空穴的尺寸不同，并在接觸表面隨機分布；

(3)忽略接觸過程中相鄰微凸體間的相互作用、微凸體間的摩擦力、接觸強化作用以及硬度隨深度的變化；

(4)端面載荷的改變以及接觸端面的摩擦磨損不影響微空穴分布；

(5)不考慮密封間隙流體黏性的變化和流體的旋轉。

基于以上假設，機械密封端面可視為兩平面間微凸體間的相互接觸，微凸體承擔密封面載荷的作用。動、靜環接觸過程中，會產生尺寸不同并隨機分布的微空穴，如圖1所示。圖中hm為平均膜厚，用來表征密封面間的平均高度。

通過對接觸端面的簡化，機械密封的泄漏通道可視為由隨機分布的微空穴共同構成，即單個微凸體作為單個泄漏通道，研究單個微凸體在載荷作用下發生磨損后的輪廓線，得到磨損后的輪廓線函數，可求得單個泄漏通道體積流量。之后，通過面積分布函數積分后可得基于分形接觸理論的密封面整體體積泄漏率[25]：

(1)

式中：r1、r2為密封面內、外徑；p1、p2為密封面內、外側的介質壓力；D為分形維數；G為特征尺度系數；Aa為密封端面名義面積；Ar為真實接觸面積；ψ為區域擴展系數。

計算泄漏率時需要得到特定接觸載荷下的接觸面積，在接觸端面較粗糙時，在摩擦過程中載荷發生變化引起接觸面積的改變會對機械密封泄漏率產生較大影響。為了在高載荷接觸狀態下，獲得的理論接觸面積依然具有較好的結果，故此引用文獻[26]建立的粗糙表面分形接觸模型，具體表達式如下：

(2)

(3)

(4)

(5)

(6)

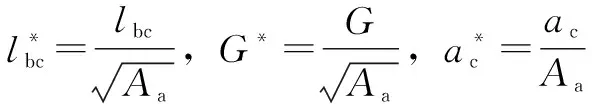
平均膜厚是密封端面形貌參數、材料性能參數、密封面的載荷以及摩擦特性參數的函數，即：

hm=h(pg,Δp,D,G,d1,d2,db,E,σ2y,f,K)

(7)

式中：pg為端面比壓；Δp為密封面內外壓差；d1和d2為密封內外徑；db為密封面平衡直徑；K=H1/σ2y為材料系數。

從式(1)可以看出，機械密封泄漏率模型建立了表面分形參數與泄漏率之間的關系。為了進一步建立分形參數與平均膜厚間的關系，還需補充泄漏率與平均膜厚間的關系。對此，文中基于泄漏率等效原則，將分形泄漏率預測模型與光滑平行端面泄漏模型進行了結合。

假設機械密封的流體運動符合流體動力學規律,泄漏通道中的流體為層流運動，HEINZE[27]建立的理想光滑平行端面泄漏模型為

(8)

式中：p1、p2為密封內外側壓力；hm為端面平均流體液膜厚度；rm為機械密封端面平均半徑；bf為密封面的寬度。

通過式(1)與式(8)，可得機械密封平均膜厚預測模型為

(9)

基于接觸模型分析對平均膜厚的影響時，由于接觸端面參數會隨時間發生變化，因此分形維數包含時間項，但時間為定值時，可不計入時間對端面參數的影響，因此可將模型簡化為

(10)

2 理論計算與分析

采用分析軟件對機械密封進行給定工況參數和密封面尺寸下的泄漏率和膜厚進行計算，模擬參數如下：密封副為SiC-浸漬石墨配對材料，密封面內、外半徑為r1=3.4×10-4m，r2=3.95×10-4m，材料彈性模量E1=410 GPa，E2=20 GPa，泊松比ν1=0.24，ν2=0.29,硬度H=30 MPa。文中模擬分析采用忽略時間后的平均膜厚模型，基于重構分形理論對給定工況進行計算。

2.1 模型驗證

模型驗證中對比模型采用泄漏預測模型，接觸分形模型采用重構接觸模型，對比兩模型泄漏率計算值及變化趨勢，驗證重構接觸模型泄漏率計算的準確性，并通過驗證平均膜厚與泄漏率變化的追隨性，以及驗證平均膜厚模型變化趨勢是否正確。

2.1.1 接觸模型驗證

在Mathematica中給定初始參數，對2種接觸模型進行泄漏率計算分析。在給定條件下，設定端面比載荷pg=0.55 MPa，材料系數K=0.5，得到分形維數和尺度系數變化下模型泄漏率，如圖2(a)所示。設定尺度系數G=1×10-9，材料系數K=0.5，得到端面比載荷和分形維數變化下模型泄漏率，如圖2(b)所示。設定尺度系數G=1×10-9，端面比載荷pg=0.55 MPa，得到材料系數和分形維數變化下模型泄漏率，如圖2(c)所示。

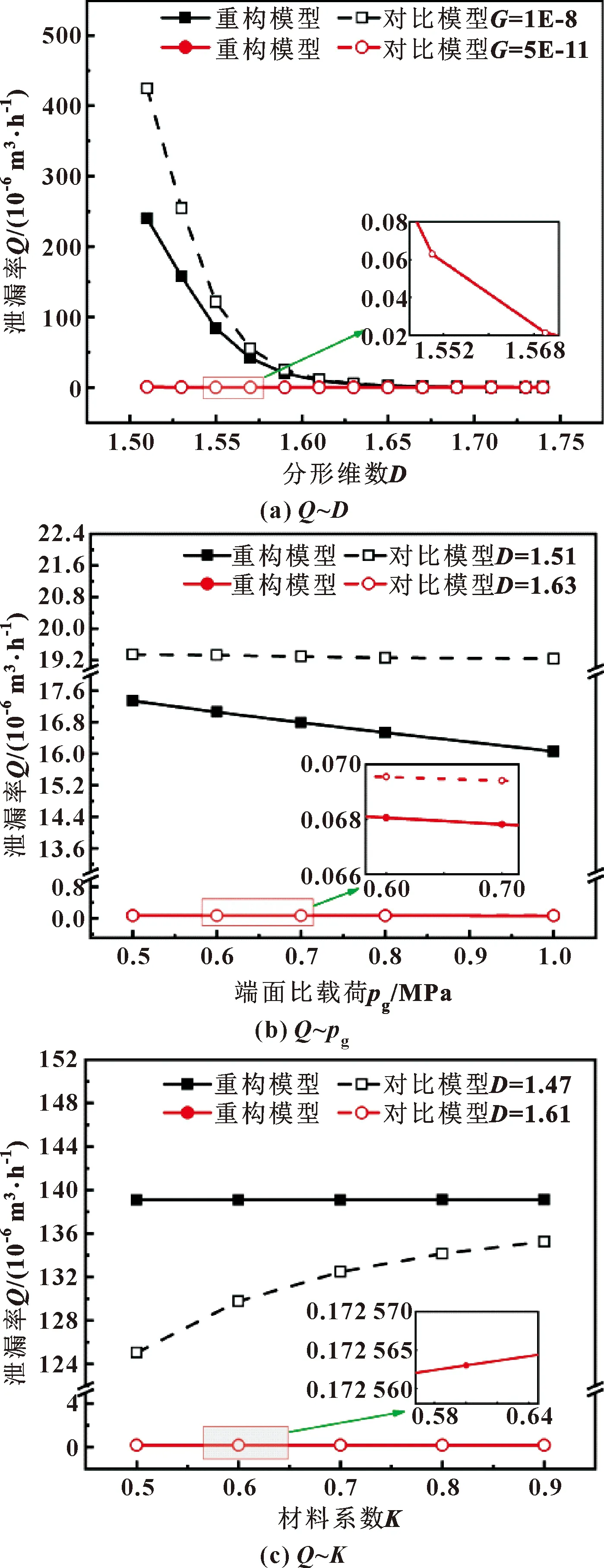
圖2 不同參數下2種模型泄漏率對比

從圖2(a)可知，在相同工況下，當分形維數較小且尺度系數較大時，兩模型數值差異較大，當兩模型分形維數與尺度系數增大后，兩模型計算結果相對誤差小于4%，并且隨著參數條件變化兩模型泄漏率變化趨勢一致。從圖2(b)所示可知，分形維數較小時，兩模型存在計算差異，分形維數增大后，兩模型數值相對誤差不超過5%。從圖2(c)可知，分形維數較小時，兩模型差異較大，隨著分形維數增大，兩模型相對誤差不超過4%。由于已有接觸模型單個微凸體函數描述中定義的接觸長度所對應的微凸體存在空白區域，且隨著接觸長度增大而增大，從而導致模型真實接觸面積與實測值有所偏差，而重構模型引入基地長度消除空白區域誤差，故在表面參數較小時，兩模型由于真實接觸面積計算結果的不同，存在差異，且重構模型計算結果更接近實測值。隨著參數增大微凸體面積的影響減小，模型數值接近且趨勢相同，文中的計算結果與對比模型的數值具有較好的吻合性，通過兩模型對比分析，驗證了模型的正確性。

2.1.2 平均膜厚驗證

在Mathematica中給定初始參數，對平均膜厚進行計算對比，通過對比平均膜厚與泄漏率的變化趨勢，驗證平均膜厚追隨性及正確性。

通過對機械密封真實工況的模擬，得到端面比載荷pg=0.55 MPa時不同表面參數下泄漏率與平均膜厚的變化趨勢，如圖3(a)、(b)所示。可以看出，隨著分形維數和尺度系數的變化，平均膜厚的變化趨勢與泄漏率變化趨勢一致，且與理論變化趨勢吻合。在給定尺度系數G=1×10-9時，得到端面載荷變化下，泄漏率與平均膜厚的變化趨勢，如圖3(c)、(d)所示。可以看出，在端面載荷改變下，平均膜厚的變化趨勢與泄漏率一致，符合理論結果，通過對比分析，驗證了模型的正確性。

圖3 不同參數下平均膜厚和泄漏率變化趨勢對比

在通過對給定工況下泄漏率模型的模擬對比，驗證了重構接觸模型泄漏率計算結果的正確性；基于重構模型對平均膜厚進行計算，驗證了平均膜厚與泄漏率的追隨性，得到基于重構模型的平均膜厚模型膜厚預測結果的正確性。

2.2 泄漏率影響參數分析

采用模擬驗證的初始參數，對機械密封端面參數改變下泄漏率的變化趨勢進行分析。在對形貌參數分析時，分別給定端面載荷pg=0.55 MPa、尺度系數G=1×10-9和材料系數K=0.5，改變端面參數，得到表面參數、端面比載荷和材料系數變化下的泄漏率變化曲線如圖4所示。

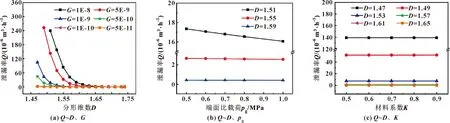
圖4 不同參數對泄漏率的影響

如圖4(a)所示，當分形維數D<1.69時，泄漏率隨著尺度系數減小而逐漸減小，在尺度系數G<1×10-9時，尺度系數變化對泄漏率影響較小;當分形維數D>1.69時，尺度系數變化對泄漏率的影響可忽略;當尺度系數一定時，分形維數增大，表面的支撐面積隨之增大，導致接觸面間的空穴面積減小，泄漏通道截面積變小，故隨分形維數增大泄漏率逐漸減小。尺度系數較小時，接觸面間的輪廓空穴較小，故泄漏通道直徑很小，流體沿程阻力較大，泄漏率較低，分形維數增大，空穴面積減小，由于輪廓空穴小，泄漏率減小趨勢較為平緩。尺度系數較大時，接觸面間輪廓空穴越大，分形維數增大，使得接觸表面更加光滑，泄漏通道截面積減小，泄漏率減小較為明顯。

其他參數一定，端面比載荷變化對泄漏率的影響如圖4(b)所示。可以看出，當分形維數D<1.55時，表面支撐面積較小，接觸面間的空穴面積較大，隨著機械密封端面比載荷增加，接觸面間空穴面積減小，泄漏率呈現下降趨勢；當分形維數D>1.59時，表面支撐面積較大，空穴面積較小，端面比載荷增大不足以導致微凸體大面積變形，故泄漏率隨著端面比載荷的增大，近似保持不變。

在給定其他參數，得到材料系數對泄漏率的影響，如圖4(c)所示。材料系數表征硬度，分形維數較小時，隨著材料系數增大，泄漏率增大；由于材料系數變化對接觸面積的影響較小，分形維數增大時，隨著材料系數變化，泄漏率未發生明顯改變。

通過分析可得，端面分形維數越大，尺度系數越小，密封性越好。在其他參數給定時，端面比載荷對密封泄漏率的影響可忽略不計。通過分析材料系數影響可以得出，在機械密封性能研究中，可以忽略材料系數改變下密封泄漏率的變化。

2.3 平均膜厚影響參數分析

在對機械密封平均膜厚分析時，分別給定端面載荷pg=0.55 MPa、尺度系數G=1×10-9和材料系數K=0.5，改變端面參數，得到表面參數、端面比載荷和材料系數變化下的平均變化曲線，如圖5所示。

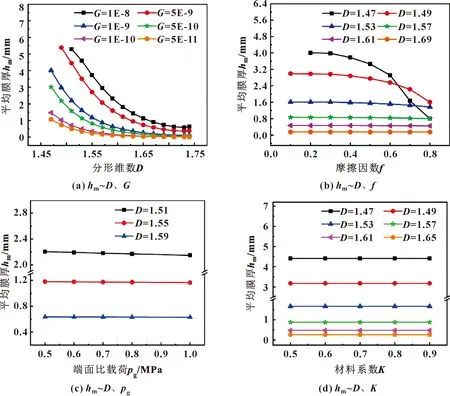
圖5 不同參數對平均膜厚的影響

從圖5(a)可以看出，隨著分形維數增大，平均膜厚不斷減小;增大尺度系數，機械密封平均膜厚不斷增大，平均膜厚增量比隨分形維數增大而不斷減小。但此時，平均膜厚隨尺度系數變化較為平緩。在給定尺度系數時，隨分形維數的增大，平均膜厚逐漸減小，并在分形維數增大的過程中，平均膜厚的變化趨于平穩且近似保持一致。

圖5(b)所示為其他參數一定時摩擦因數對泄漏率的影響。可以看出，在分形維數D<1.61時，隨著摩擦因數增大，平均膜厚逐漸減小，并且平均膜厚在f=0.6附近變化較為明顯；當分形維數D>1.61后，摩擦因數變化對平均膜厚的影響可忽略。

從圖5(c)可以看出，分形維數較小時，端面比載荷的改變會對泄漏率產生影響，隨著載荷增大，平均膜厚逐漸減小；在分形維數D>1.55時，端面比載荷改變，平均膜厚近似保持不變。從圖5(d)可以看，在不同分形維數下材料系數的變化對平均膜厚的影響較小。

通過對平均膜厚變化趨勢分析，由于尺度系數較小時，輪廓空穴小，泄漏通道的直徑較小，故參數變化對平均膜厚變化的影響較小，可得平均膜厚的變化趨勢在尺度系數較小時較為平緩。分形維數較小時，空穴面積較大，改變端面比載荷，導致空穴面積變化，平均膜厚隨之改變，在分形維數較小時，需計入端面比載荷的影響。分形維數較大時，空穴面積較小，端面比載荷對空穴面積影響較小，在分形維數較大時，其變化可忽略。材料系數表征硬度，對接觸過程中空穴面積變化的影響可忽略，在分形維數較小時，材料系數變化對平均膜厚的影響仍可忽略。

3 結論

(1)基于重構分形粗糙接觸模型，結合機械密封泄漏預測模型，建立了機械密封平均膜厚預測模型。

(2)分形維數較小時，泄漏率隨著尺度系數減小以及端面比載荷增大而逐漸減小。當分形維數D>1.69后，尺度系數和端面比載荷變化對泄漏率影響可忽略，并且材料系數對泄漏率的影響可忽略。

(3)分形維數較小時，尺度系數、端面比載荷以及摩擦因數的改變會對平均膜厚產生影響，當分形維數過大時，平均膜厚逐漸減小，上述參數對平均膜厚的變化可忽略。