基于改進SIFT和位置方向距離函數的胃腸道圖像匹配算法*

李俊憓，張永順

（大連理工大學精密與特種加工教育部重點實驗室，遼寧大連 116024）

0 引言

膠囊機器人替代了傳統內窺鏡對患者進行無痛無創的胃腸道便利檢查。在檢查過程中，姿態信息十分重要，準確的姿態信息對于醫生判斷病變區域起到很大幫助[1]。而基于視覺的位姿檢測，需要對胃腸道圖像進行圖像匹配以獲取位姿信息[2]。圖像匹配是指在兩張或者多張圖片中尋找一致點的過程，在機器視覺、機器人定位、醫療等領域有著廣泛的應用[3-4]。膠囊機器人拍攝的胃腸道圖像圖幅小、圖像姿態不穩健以及胃腸道自身存在因紋理復雜、顏色差異和成像條件導致的非線性灰度差異，導致匹配過程中出現正確匹配對較少，且匹配時間較長的問題。而匹配結果的質量，直接影響到后續位姿信息處理的準確性，甚至會加大處理難度。

目前，圖像匹配算法主要分為兩類：基于圖像區域的圖像匹配和基于圖像特征的圖像匹配。前者主要依靠像素強度之間的相似行關系來確定圖像間的對應關系[5]，常用的相似性關系有互相關和互信息，但這種匹配方法計算復雜度較高，容易受到噪聲干擾，匹配效果較差。后者是在參考圖像中提取特征，采用相似性度量和一些約束條件確實幾何變換，并將該變化應用于待匹配圖像[6]，其中最為經典的是SIFT（尺度不變特征變換）[7]。SIFT算法對于圖像縮放、平移、旋轉、尺度等具備不變性，但SIFT算法比較復雜，計算繁瑣，耗時較長[6]。此外也有一些算法被提出，如SURF[8]、ORB[9]和GLOH[10]等，主要是在計算速度上進行了提高。當SIFT算法直接應用與胃腸道圖像時，由于非線性灰度差異的存在，使得匹配精度很低。目前尚未有專門針對胃腸道圖像的匹配算法研究，這一方面仍是空白。

本文提出了一種基于改進SIFT和位置方向的胃腸道圖像匹配算法，利用新的梯度定義克服了胃腸道圖像間的灰度差異，采用對數極坐標完成了描述子的降維，提高計算效率。此外，結合特征的位置和方向建立了魯棒性更強的距離匹配函數，以獲取更多的正確匹配對。

1 SIFT算法

SIFT算法是由Lowe于2004年提出的一種圖像匹配算法，主要包括以下幾個部分。

（1）尺度空間極值檢測：利用高斯卷積核函數計算不同尺度下的高斯尺度空間以得到高斯金字塔圖像，將高斯金字塔的相鄰層相減構造高斯差分金字塔（Difference of Gaussians，DoG）[11]。

（2）特征點定位：將每一個像素點與它的所有相鄰點對比確定極值點，然后利用泰勒公式將DoG在局部極值點展開計算極值的偏移量，若偏移量過小則該極值點需要剔除，剩下的就是特征點[4]。

（3）特征點主方向的確定：利用特征點鄰域范圍的像素梯度幅度和方向直方圖為每一個特征點確定主方向[11]。

（4）確定特征點描述子：將特征點鄰域劃分成4×4的子區域，在每個子區域選取8個方向進行計算，因此每個特征點可以生成一個4×4×8=128維的描述子。

2 改進后的SIFT算法

對SIFT算法進行改進主要體現在兩個方面：（1）對梯度進行重定義，采用SOBEL算子重新計算胃腸道圖像的梯度和主方向，以消除非線性灰度差異；（2）利用GLOH和對數極坐標構建描述子，完成描述子的降維處理。改進的SIFT算法流程如圖1所示。

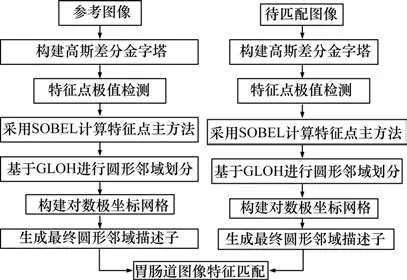
圖1 胃腸道圖像特征的檢測流程

2.1 新的梯度定義

SIFT算法中采用下式進行像素梯度幅度和梯度方向的計算：

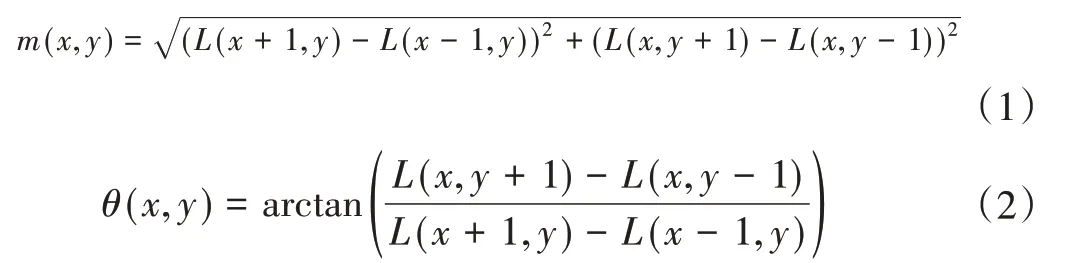
式中：I(x,y)為圖像位于(x,y)的像素值；m(x,y)為像素梯度幅值；θ(x,y)為像素梯度方向。

由于胃腸道的特殊管腔結構，腔內比周圍環境要暗。由于非環境照明，靠近光源的組織成像時非常明亮，使得胃腸道圖像之間存在非線性的灰度差異。特征描述子由特征點鄰域的像素梯度直方圖構成[12]，而胃腸道圖像的非線性灰度差異會導致參考圖像和待匹配圖像相同區域的像素梯度具備較大差異。圖2（a）和圖2（b）分別為參考圖像和待匹配圖像的像素梯度幅值圖和像素梯度方向圖。通過分析可發現在使用傳統梯度定義時，兩幅圖像在藍色圓形區域的梯度幅值相似性較大，而梯度方向差異較大，這種差異導致了圖像在特征識別中存在了誤差，對特征點的主方向帶來了一定誤差。而特征描述子是利用了特征點的主方向來保證旋轉不變性，梯度主方向誤差使得提取的描述子準確性降低，在匹配階段出現問題，因此需要對該算法的像素梯度計算方法進行改進。

圖2 原梯度方法得到的梯度幅值和梯度方向

為改善特征描述的魯棒性，本文對胃腸道圖像梯度的計算采用二階SOBEL進行計算。首先，在高斯尺度空間圖像上計算像素梯度，計算公式如下：

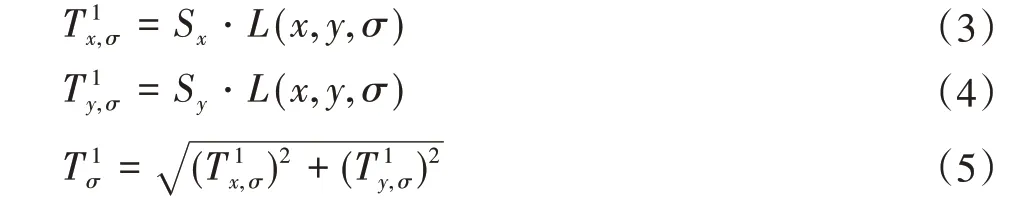
式中：L(x,y,σ)為高斯尺度空間；和分別為一階高斯尺度空間沿水平方向和豎直方向的差分；為高斯尺度空間的梯度幅度；S為SOBEL算子；σ為尺度。

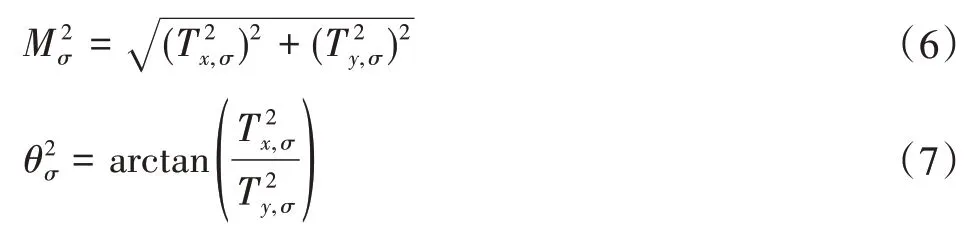
圖3所示為使用二階SOBLE算子重新計算梯度后得到的圖2中胃腸道的梯度幅度和梯度方向圖像。從圖3中的圓形區域可知道，不僅相同區域的梯度幅度圖像有較好的一致性，并且該區域的梯度方向圖像也有較好的一致性，因此可以確定采用新的梯度定義計算方法可消除胃腸道圖像的非線性灰度差異，為后續精準匹配奠定了基礎。

圖3 新梯度方法得到的梯度幅值和梯度方向

2.2 對數極坐標描述子生成

對數極坐標可將圖像由笛卡爾坐標系描述轉換到對數極坐標描述[13]，這樣的轉換使得圖像的尺度和旋轉變換變為平移變化，降低了匹配難度，可提高匹配精度，能更好地處理亮度變化等問題。GLOH（梯度方向直方圖）是一種利用笛卡爾坐標和對數極坐標確定網格生成圓形鄰域。本文采用采用基于GLOH的半徑為12σ′圓形鄰域和有13個子區域的對數極坐標網格生成特征描述子。圓形鄰域如圖4（a）所示，針對胃腸道圖像，當R3和R2與R1的比率分別是0.25和0.65時，此時比率設置為最佳結果。對數極坐標網格如圖4（b），水平方向代表極角。對兩個外層圓形區域6等分，一共得到13個子區。再按照45°一個方向的原則計算每個扇區內的特征點維度數目，共計8個維度。最終累計獲得每個特征維度為104維的對數極坐描述子。

圖4 圓形鄰域和對數極坐標網格示意圖

3 位置方向歐式距離匹配

最近鄰與次進鄰比匹配是常用的特征匹配算法，這種算法是尋求兩個對應點之間的最近歐式距離與次進歐式距離，當二者比值大于某一設定值時，認為是錯誤匹配進行刪除，剩下就是正確匹配對。這種方法在胃腸道圖像中可獲得比較精確的對應關系，但沒有考慮到特征的位置變換和方向偏移，使得很多特征點找不到正確的匹配對。因此，本文提出了基于位置方向歐式距離（Position Orientation Euclidean Distance，POED）函數來計算匹配對。首先需要構建POED函數，隨后采用MS和RANSAC算法對錯誤匹配對進行篩選，以獲得更多正確的匹配對。

3.1 POED函數確定

位置方向歐式距離函數是結合特征點的位置方向信息來進行建立，需要確定特征點的位置變換誤差和主方向偏移誤差。

從參考圖像和待匹配圖像獲得的特征點集合分別為P=p1，p2，p3，…，pm和P′=p′1,p′2,p′3,…,p′n。(x′j,y′j)和θ′j分別代表待匹配圖像中特征點p′n的位置和方向；(xi,yi)和θi分別代表參考圖像中特征點pm的位置和方向；pm點和p′n點之間的位置變換誤差是：

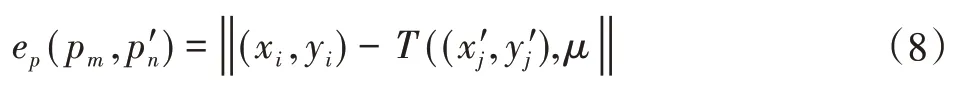
式中：T(*)為相似變換模型；μ為相似模型變換參數。

pm點和p′n點之間的主方向誤差為：

式中：Δθ*為主方向差直方圖的峰值位置。

基于以上兩個誤差定義一個穩健性更好的特征匹配距離，即位置方向歐式距離（POED），公式如下所示：

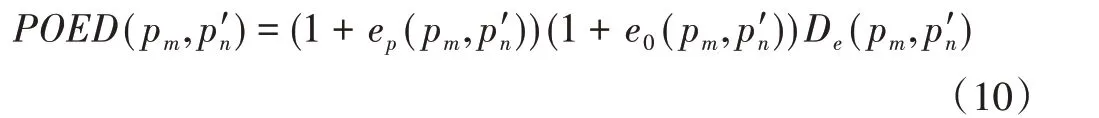
式中：D e(p m,p′n)為兩特征點之間的歐式距離。

3.2 匹配過程

（1）粗匹配：采用最近鄰與次近鄰比匹配進行胃腸道圖像的特征匹配，獲得初始匹配點對集合P1，并計算主方向差，水平位移，豎直位移和尺度比的直方圖，從圖中獲取峰值位置Δθ*、Δx i、Δy i、r*。采用隨機抽樣一致（RANSAC）算法進行錯誤匹配對的刪除并計算初始變換參數μ。

（2）精匹配：采用POED作為描述子的距離度量，并再次使用最近鄰與次近鄰比的特征匹配方法進行匹配，至此，完成了兩次匹配并獲得了匹配對集合P2。

（3）錯誤匹配對刪除：在完成圖像的特征點匹配后，會出現一些誤匹配點。要解算出正確的匹配關系，需要去掉誤匹配點，主要采用MS算法和RANSAC算法進行錯誤點刪除。MS算法是指在變換空間中，將每個特征點和與其對應的位置，方向進行聯系，采用模式搜索的方式消除弱匹配關系的方法。具體操作如下：令(xi,yi)和(x′i,y′i)分別為匹配對P2中第i個匹配點的位置坐標，其相應的水平位移和垂直位移定義如下：

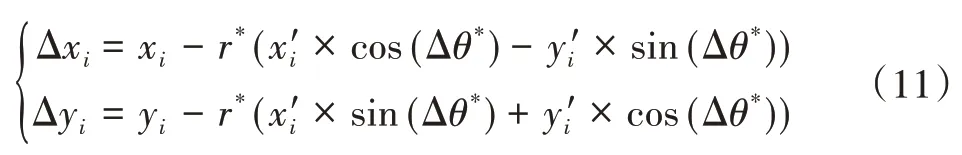
采用上述公式進行錯誤點刪除后得到匹配點集合P3，在使用RANSAC算法刪除P3中的錯誤對應對，隨后即可得到正確的匹配關系。RANSAC算法是指在有錯誤匹配的匹配集合中，不斷進行迭代已刪除錯誤匹配對，提高匹配精度。特征匹配流程如圖5所示。

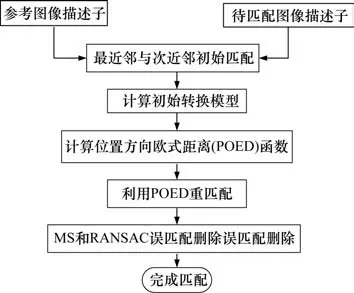
圖5 特征匹配流程

4 胃腸道圖像匹配結果

4.1 實驗圖像

為評估本文提出算法的有效性，采用雙半球膠囊機器人獲取胃部圖像與腸道圖像進行特征匹配。考慮到本文算法是針對胃腸道圖像開發的，加上在匹配階段，定義了POED函數，因此將本文算法定義為GIPOED-SIFT。本文算法與其他算法做了對比實驗，如：SIFT，PSOSIFT，SURF+FLANN，ORB+FLANN；本文還專門比較了“新的梯度定義+FSC”算法來確定對于胃腸道圖像非線性灰度差異的處理。硬件開發環境為Intel（R）Core（TM）i5-7300HQ CPU@2.50GHz、內存為16GB的PC，軟件開發環境為Microsoft Visual Studio 2019和計算機視覺庫OpenCV 3.4.1。

4.2 評價標準

采用均方根誤差（Root Mean Square Error，RMSE）進行算法評估[5]，其公式如下：

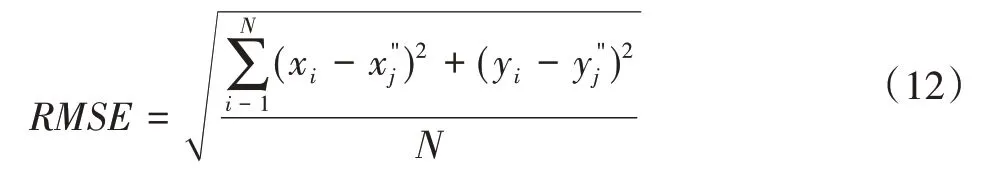
式中：N為選取的匹配點個數；(xi,yi)和(x′i,y′i)為第i個匹配點的坐標；(x"

i,yi")為第i個待匹配圖像特征點(x′i,y′i)在經過匹配幾何關系后轉換的坐標。

4.3 實驗結果

如圖6～7和表1所示，給出了GIPOED-SIFT算法與其他算法在胃腸道圖像的實驗結果，可以發現在匹配時間上，GIPOED-SIFT算法相比于SURF，ORB等算法耗時較長，但對比其他算法耗時較短，這是由于GIPOEDSIFT算法主要耗時在匹配階段，需要對特征點進行二次匹配并進行新的匹配距離計算，這導致了其耗時較長，但匹配時間在3 s以內，可以滿足姿態檢測實時性要求；從圖6（a）和圖7（a）中可以看出，GIPOED-SIFT算法可以正確匹配胃腸道圖像，并且不存在誤匹配點，相比于其他算法而言，匹配的特征數目較少，但匹配點的準確率遠遠高于其他算法，并且匹配點數目滿足相機本質矩陣求解，不會對姿態估計帶來匹配誤差；從匹配誤差來看，本文算法在胃腸道圖像匹配中RMSE均為最小。為了驗證新的梯度算法針對胃腸道圖像非線性灰度差異的有效性，實驗中對比了“新的梯度定義”和“SIFT”算法，可以發現新的梯度應該可以減小匹配誤差，增強匹配對正確數目。從以上可以看出，本文提出的匹配算法在胃腸道圖像匹配中匹配精度、匹配時間上相比于SIFT算法得到了顯著提高，滿足了姿態檢測實時性要求，可用于姿態檢測的特征匹配。

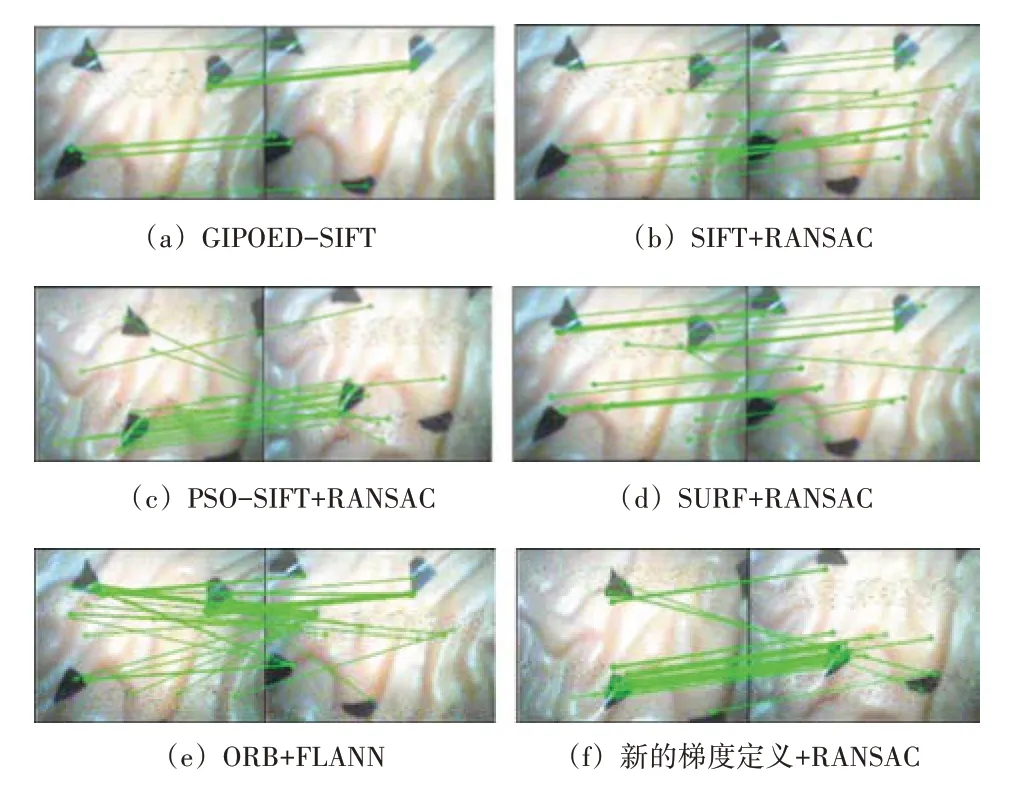
圖6 胃部圖像匹配結果

圖7 腸道圖像匹配結果

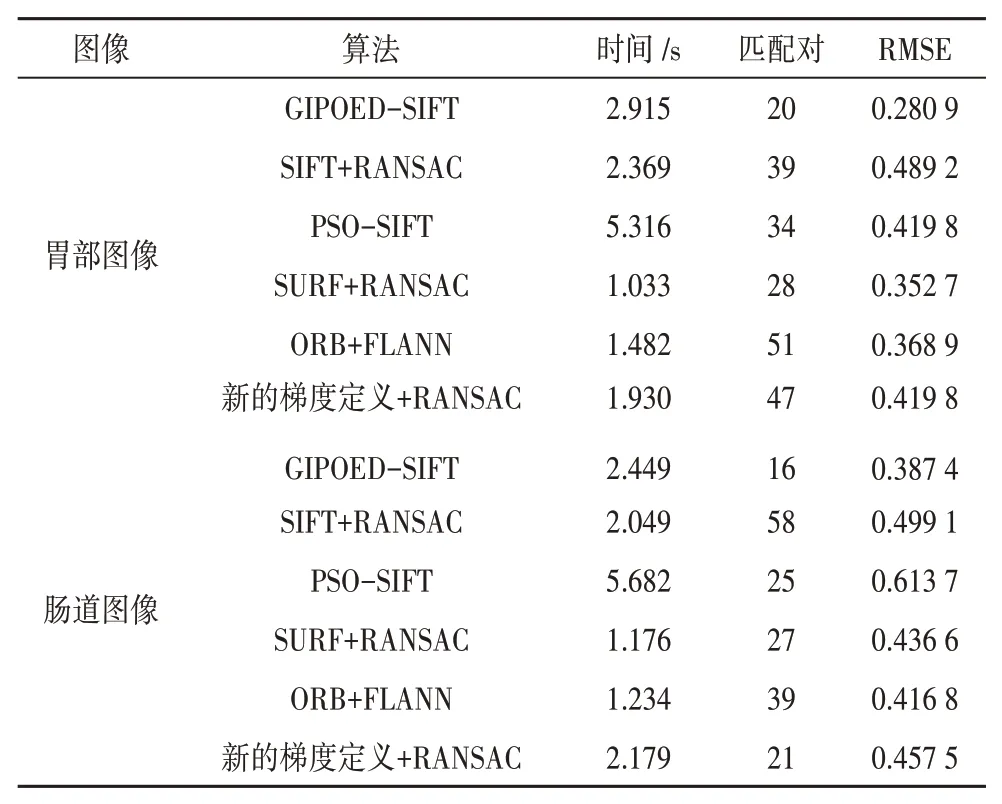
表1 本文提出的算法和對比算法實驗結果

5 結束語

本文提出了一種聯合SIFT和特征點位置方向距離的胃腸道圖像匹配算法。首先采用新的梯度定義消除了胃腸道圖像的非線性灰度差異；此外在特征描述子生成階段，利用對數極坐標進行構建，對描述符進行了降維，使得匹配更為穩健；最后提出了一種結合每個特征點的位置和方向來增加正確匹配對數的穩健匹配算法。在胃腸道圖像上的實驗結果表明，本文提出的算法與其他算法進行比較后，在匹配精度和正確匹配數目方面均得到提升，可為膠囊機器人位姿求解提供精確位姿信息。