汽車起重機泵閥復合系統高性能控制研究*

和進軍，賈鵬碩，唐琛淇，李 凱，謝 帥，艾 超

（1.三一汽車起重機械有限公司，長沙 410600;2.燕山大學機械工程學院，河北秦皇島 066004）

0 引言

汽車起重機具備機動性能強、承載能力大、適用范圍廣等多方面的突出優勢，在建筑工地、橋梁交通、港口搭建等多方向工程領域中實現了廣泛應用[1]。目前起重機控制系統普遍采用傳統的負載敏感液壓系統，但負載敏感系統需要預設一定的壓力裕度實現泵口壓力閉環控制，導致這部分壓力均損失在壓力補償閥和換向主閥上，使得系統能耗較大[2]。泵閥復合控制系統是通過永磁同步電機和比例閥的協同控制實現起重機變幅伸縮機構的單獨和復合動作，節能效果好。但由于系統中存在永磁同步電機轉速波動、液壓泵流量非線性等因素，使得變幅伸縮機構的控制精度不高，動態性能受限[3-4]。

李銳等[5]提出了改進徑向基函數（RBF）神經網絡PID控制方法，設計了負載敏感平衡閥，經過實驗證明，能夠有效改善系統控制精度。Sakaino和Tsuji[6]提出基于反饋調節器和擾動觀測器，設計控制器以消除摩擦力干擾，增強了液壓系統的魯棒性。Ren等[7]利用系統識別提出了低帶寬線性控制器，獲得良好的魯棒性，可以降低噪聲，消除未建模的高頻動力學影響。韓小霞等[8]針對泵控系統控制精度低的問題，對泵控系統流量死區數學模型進行研究，提出動態逆補償的方法，改善了控制性能。付永領等[9]針對泵控系統參數不確定性擾動的問題，通過對系統內存在的摩擦特性的分析，設計新型的自適應模糊控制算法，使得跟蹤速度得到提高。Helian B等[10]通過實際擬合提出了非線性泵流速圖，將所需泵流量的適當非線性補償將其用于控制器設計，實現了高性能控制。

本文以起重機變幅伸縮機構為研究對象，對電機泵組輸出流量控制進行研究。詳細介紹了泵閥復合控制系統的工作原理，建立流量控制數學模型，針對系統中存在的電機轉速波動、泵輸出流量非線性等影響因素，將模糊算法動態響應好、魯棒性強的特性和傳統PID穩態精度高、穩定可靠的優點進行整合，提出模糊PID線性復合控制器，最后通過與傳統PID控制的仿真對比驗證了該方法的有效性，提高了系統流量控制性能。

1 泵閥復合控制系統

汽車起重機變幅伸縮泵閥復合控制系統液壓原理如圖1所示。

圖1 泵閥復合控制系統液壓原理Fig.1 Hydraulic principle of pump and valve compound control system

系統將變幅伸縮電手柄信號反饋到控制器中，控制器進而判斷變幅伸縮機構處于單動還是復動狀態。當系統處于單獨動作時，控制器根據手柄的開度大小給定電機相對應的轉速值，通過泵口流量傳感器信號反饋，實現對流量的控制，比例主閥開度最大，僅實現換向。當系統處于復合動作時，控制器計算變幅伸縮機構所需的總流量，進而給定電機轉速，使得液壓泵輸出基礎流量，變幅伸縮機構各自所需的流量再由比例主閥進行調節，實現泵閥復合協同控制。

在傳統的負載敏感系統中，輸入到變幅伸縮機構的流量僅由比例主閥調節，非線性影響因素少。而泵閥復合控制系統在閥控系統的基礎上，又加上泵控系統，電機轉速波動、液壓泵流量非線性等因素嚴重影響了系統的控制性能。所以本研究主要針對泵控系統的控制理論進行研究，改善流量控制的動態響應和控制精度。

2 泵閥復合控制系統電機泵組數學模型

2.1 永磁同步電機

永磁同步電機負責將控制輸入電壓轉化成電機輸出轉速，電機輸出轉速與輸入電壓信號之間的關系為：

式中：Uq為電機q軸電壓，V；Rs為電機繞組阻值，Ω；L q為q軸電感，H；iq為q軸電流，A；ωm為電機輸出轉速，rad/s；Ke為永磁體反電動勢系數，V/（rad·s-1）；Te為電機扭矩，N·m；Kt為電機扭矩系數，N·m/A；TL為液壓泵產生的反扭矩，N·m；Dp為液壓泵排量，m3/rad；pL為液壓泵兩腔壓差，pL=pA－pB，Pa；Jm為電機泵轉動慣量，kg·m2；Bm為電機泵運動副產生的與ωm相關的摩擦因數。

整理式（1）得：

2.2 液壓泵

考慮油液壓縮與內外泄漏等因素分析定量泵流量分布特性，如圖2所示。

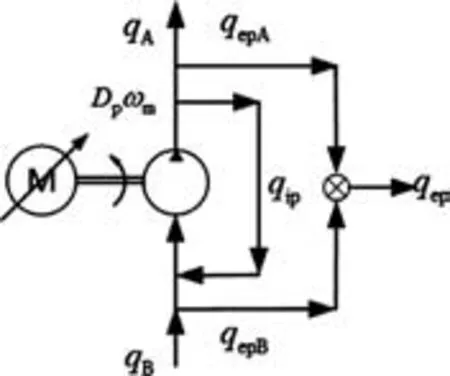
圖2 液壓泵流量分布Fig.2 Flow distribution of hydraulic pump

假定液壓泵的泵容積排量為常數，從泵到被控液壓缸的兩腔負載容積流量可表示為：

式中：qA為系統流量，m3/s；qB為泵吸入的油箱油液流量，m3/s；Cip為泵的內泄漏系數，（m3·s-1）/Pa；Cep為泵的外泄漏系數，（m3·s-1）/Pa；pA為系統負載壓力，Pa；pB為標準大氣壓力，Pa。

聯立式（2）、式（3）可以得到泵閥復合控制系統由輸入電壓Uq到輸出流量qA的數學模型。

3 模糊PID控制器設計

常規PID控制具有較高的精度，良好的穩定性，但面對系統多種非線性干擾，適應性較差；模糊控制動態性能較好，適應能力強，卻無法獲得較高的穩態精度，可能會發生震蕩。所以研究將兩種方法進行組合，形成模糊PID線性復合控制結構，如圖3所示。

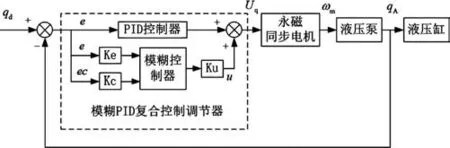
圖3 模糊-PID復合控制結構Fig.3 Block diagram of fuzzy-PID compound control structure

（1）模糊控制器結構

采用二輸入一輸出構架。輸出量為控制量u，輸入量為系統給定流量qd和泵出口反饋流量qA的偏差e和偏差變化率ec，將復合控制器輸出傳輸給電機，進而控制系統流量。

（2）輸入和輸出變量論域

設定ec和u的模糊集合為：

{NB，NM，NS，O，PS，PM，PB}

設定偏差e的模糊集合為：

{NB，NM，NS，NO，PO，PS，PM，PB}

為了得到更高的精度需求，將O分成了NO、PO兩個部分。

（3）模糊制規則表和隸屬函數

模糊控制規則的建立是模糊推理法能成功應用的保證，模糊推理符合一般推理方法的邏輯。模糊控制規則如表1所示。可以通過模糊量賦值得到e、ec以及u的隸屬函數，再利用MATLAB模糊工程箱結合隸屬函數得到輸出曲面圖，如圖4～7所示。

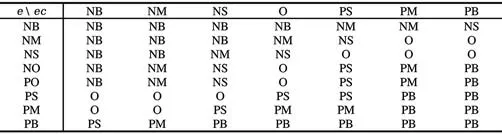
表1 模糊控制規則Tab.1 Fuzzy control rule list

圖4 模糊控制對于偏差為e的隸屬函數圖像Fig.4 Fuzzy control for the deviation of e membership function image

圖5 模糊控制對于偏差為ec的隸屬函數圖像Fig.5 Fuzzy control for the deviation of ec membership function image

圖6 模糊控制對于控制量為u的隸屬函數圖像Fig.6 Fuzzy control for the control quantity u membership function image

圖7 模糊控制綜合輸出曲面Fig.7 Fuzzy control integrated output surface diagram

4 系統仿真分析

4.1 仿真模型建立

利用Simulink構成模糊PID線性復合控制系統和傳統PID控制系統仿真模型，如圖8～9所示。

圖8 PID控制仿真模型Fig.8 PID control simulation model diagram

在Simulink仿真過程中，模型參數設置是十分重要的一部分，整體參數賦值結合元件技術樣本，得到其系統參數如表2所示。

表2 仿真模型參數Tab.2 Simulation model parameter Tab

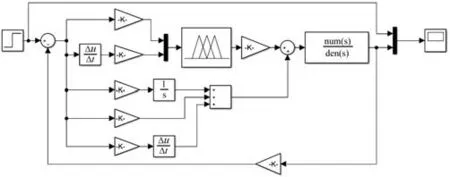
圖9 模糊PID復合控制仿真模型Fig.9 Simulation model diagram of fuzzyPID compound control

利用Simulink模糊控制箱，運用試湊法對模糊PID控制器與傳統PID控制器中的參數進行調整，能夠得到控制過程中最佳的各個參數的值。

模糊PID復合控制器的偏差因子KE、偏差變化因子KEC以及控制量因子KU分別是0.45、0.003、50，其中PID參數為：Kp0=900，Ki0=2，Kd0=1；傳統PID控制器參數為：Kp=800，Ki=2，Kd=1。

4.2 60 L/min階躍仿真分析

給定泵閥復合控制系統一個60 L/min的階躍信號，得到傳統PID控制系統的階躍響應及其偏差曲線，如圖10～11所示。

圖10 PID控制階躍響應曲線Fig.10 PID control step response curve

圖11 PID控制階躍響應偏差曲線Fig.11 PID control step response deviation curve

模糊PID線性復合控制系統的階躍響應及偏差曲線如圖12～13所示。

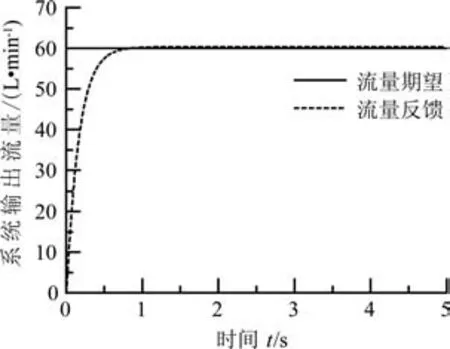
圖12 模糊-PID線性復合控制階躍響應曲線Fig.12 Step response curve of fuzzy-PID linear compound control

圖13 模糊-PID線性復合控制階躍響應偏差曲線Fig.13 Step response deviation curve of fuzzy-PID linear compound control

為了分析方便，將實際系統流量輸出曲線和期望流量曲線放到同一界面顯示，通過60 L/min流量階躍響應曲線進行分析，可以得出以下結論：傳統的PID控制器動態響應速度較慢，在2 s后系統才逐漸趨于穩定，而且穩態誤差比較大，達到了0.67 L/min。而模糊PID線性復合控制器在1.5 s后系統便趨于到達穩態，且輸出流量精度可以控制到0.34 L/min以內。

4.3 120 L/min階躍仿真分析

給定泵閥復合控制系統一個120 L/min的階躍信號，傳統PID控制系統的階躍響應及偏差曲線如圖14～15所示。

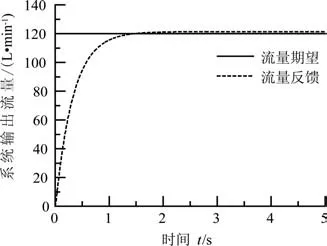
圖14 PID控制階躍響應曲線Fig.14 PID control step response curve

模糊PID線性復合控制系統的階躍響應及偏差曲線如圖16～17所示。

圖16 模糊-PID線性復合控制階躍響應曲線Fig.16 Step response curve of fuzzy-PID linear compound control

圖15 PID控制階躍響應偏差曲線Fig.15 PID control step response deviation curve

圖17 模糊-PID線性復合控制階躍響應偏差曲線Fig.17 Step response deviation curve of fuzzy-PID linear compound control

對流量控制系統在PID控制器、模糊PID線性復合控制器下的120 L/min流量階躍響應曲線進行分析，可以得出以下結論：傳統的PID控制器動態響應速度較慢，在2.5 s后系統才逐漸趨于穩定，而且穩態誤差比較大，達到了1.33 L/min。而模糊PID線性復合控制器在1.8 s后系統便趨于到達穩態，且輸出流量精度可以控制到0.68 L/min以內。

4.4 180 L/min階躍仿真分析

當給定泵閥復合控制系統一個180 L/min的階躍信號時，傳統PID控制系統的階躍響應曲線如圖18所示，階躍響應偏差曲線如圖19所示。

圖18 PID控制階躍響應曲線Fig.18 PID control step response curve

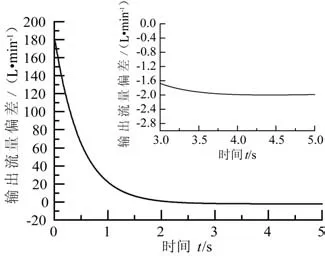
圖19 PID控制階躍響應偏差曲線Fig.19 PID control step response deviation curve

模糊PID線性復合控制系統的階躍響應及偏差曲線如圖20～21所示。

圖20 模糊-PID線性復合控制階躍響應曲線Fig.20 Step response curve of fuzzy-PID linear compound control

圖21 模糊-PID線性復合控制階躍響應偏差曲線Fig.21 Step response deviation curve of fuzzy-PID linear compound control

對流量控制系統在PID控制器、模糊PID線性復合控制器下的180 L/min流量階躍響應曲線進行分析，可以得出以下結論：傳統的PID控制器動態響應速度較慢，在3.5 s后系統才逐漸趨于穩定，而且穩態誤差比較大，達到了1.98 L/min。而模糊PID線性復合控制器在2.5 s后系統便趨于到達穩態，且輸出流量精度可以控制到1.02 L/min以內。

綜合以上可以判斷，相比傳統PID控制器，系統在模糊PID線性復合控制器下的流量輸出不僅動態響應快，且具有更好的穩態精度。

5 結束語

本文以起重機變幅伸縮機構為研究對象，針對泵閥復合控制系統因受到永磁同步電機轉速波動、液壓泵流量非線性等因素影響而出現的精度不高，動態性能受限問題進行研究，得到結論如下。

（1）搭建泵閥復合控制系統電機泵組非線性數學模型，設計一種模糊PID線性復合控制器并利用模糊工程箱在Simulink中完成控制器仿真模型搭建。

（2）分別對PID控制系統和模糊PID線性復合控制系統輸入流量階躍信號進行仿真，基于仿真結果可知，對比PID控制系統，本研究提出的模糊PID線性復合控制器使得泵閥復合控制系統動態響應時間縮短0.5～1 s，流量穩態精度提升50%，有效改善了泵閥復合控制系統的控制性能。