異構多基地雷達直線柵欄覆蓋的布站優化方法

李海鵬， 馮大政， 陳少鋒

(1.西安電子科技大學 雷達信號處理國家重點實驗室， 陜西 西安 7100071;2.西安電子工程研究所 總體一部， 陜西 西安 710100；3.武警工程大學 教研保障中心， 陜西 西安 710086)

0 引言

柵欄覆蓋在無線傳感器網絡(WSN)的應用中有著極其重要作用與地位，其廣泛應用于工業、經濟、軍事等諸多領域。近年來，基于雷達的WSN被用于對重點區域進行探測與監控。為能夠檢測到以任意路徑進重點區域的入侵者，通常需要利用雷達網絡構建一個連續的雷達柵欄覆蓋。

傳統的雷達柵欄覆蓋是基于圓盤或扇形覆蓋模型而構建的，在這些模型中發射器與接收器共置，通常稱其為單基地雷達。但是單基地雷達發射器利用率不高、安全性較差。相對的，多基地雷達由若干分開放置的發射器和接收器構成，具有抗干擾、抗反輻射導彈、反隱身、反低空突防能力強等特性，在性能上和成本上相比于單基地雷達更具有優勢。由于發射器和接收器的布站位置對多基地雷達的覆蓋區域有直接影響，因此近年來關于多基地雷達的布站優化問題受到了廣泛關注。根據應用場景不同，布站優化問題可分為直線(帶狀)柵欄覆蓋和圓周(圓環帶)柵欄覆蓋。文獻[11]以布站成本最小化為準則構建帶狀柵欄覆蓋,并研究了雷達布站的容錯和節能問題；文獻[12]構建K柵欄覆蓋；文獻[13]構建點目標柵欄覆蓋；文獻[14-18]基于直線構建帶狀柵欄覆蓋，使得布站總成本最小；文獻[19-20]以最小化布站總成本為準則，分別研究圓周型柵欄覆蓋問題和具有給定寬度的圓環型柵欄覆蓋問題。同時，以上文獻均假設發射器和接收器的性能參數都分別相同，即為同構多基地雷達(HMMR)。而實際應用中由于布站位置受限的原因，基于HMMR的優化結果可能不易實現。利用含有不同發射器的多基地雷達網絡進行布站，即采用異構多基地雷達(HTMR)，則可以適應更復雜的應用場景。如圖1(a)所示，假設兩條曲線之間為限制區，雷達不能布置在該范圍內，此時基于HMMR的布站結果不符合實際應用要求。相對的，在圖1(b)中，采用HTMR的布站方法可以避開限制區。、是兩種不同的發射器，其中紅色發射器為異構發射器，,…,為接收器。

圖1 雷達網絡構建柵欄覆蓋示意圖Fig.1 Barrier coverage diagram of the radar network

文獻[21]基于HTMR進行研究，主要討論了直線柵欄覆蓋的布站問題，通過仿真實驗表明HTMR的最優布站結果依賴于不同發射器的布站次序，指出從理論上給出如何確定這一最優次序是十分困難的。因此，如何優化HTMR網絡的布站位置，使得成本最小是一個值得研究和探討的問題。本文受文獻[21]啟發，但與該文獻不同，主要有以下區別：

1) 文獻[21]對雷達傳感器的布站位置無要求與限制，本文從實際應用場景出發，考慮在布站位置受限的情況下，基于HTMR的優化布站方法。

2) 文獻[21]在仿真中采用6種HTMR(每種發射器最多只有一個)構建柵欄覆蓋，由于使用雷達種類較多，不利于實施及維護。

3) 文獻[21]方法的優化結果為近似最優，本文方法計算的布站結果是最優。

4) 本文進一步提出了基本布站模式中接收器個數上限閾值的計算方法。

1 多基地雷達基本概念與問題描述

1.1 多基地雷達覆蓋區域模型

設、分別表示雷達發射器與接收器，其組成的雙基地雷達記為(,)，位于點處的目標信噪比()為

(1)

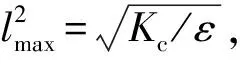
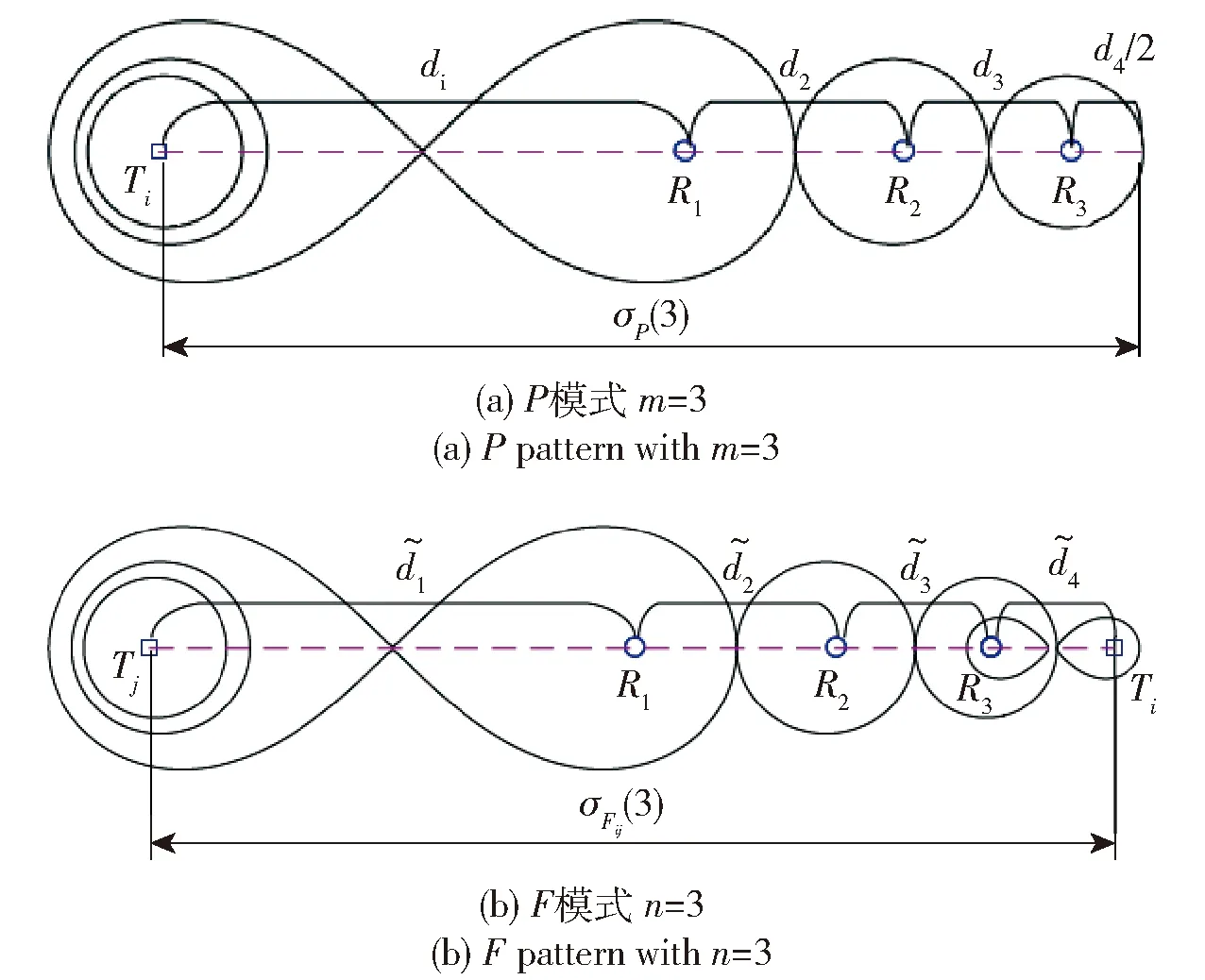
圖2 基本布站模式Fig.2 Basic deployment patterns

目標在點處可能被多組雙基地雷達探測到，記該點的最大噪聲比為()，即有

(2)

式中：由發射器所確定的常數。因此，點處的目標能被多基地雷達覆蓋的充分必要條件是()≥。

若發射器與發射器發射功率相同，記為=；若發射器的功率大于發射器，記為>。同時假設所有接收器相同，布站成本一樣，用、分別表示發射器與接收器的成本，設=為發射器與接收器成本之比。實際應用中發射器成本高于接收器，因此有>1。

1.2 直線柵欄覆蓋的基本概念

假設雷達傳感器網絡中所有發射器、接收器均部署在直線段上，以形成直線柵欄覆蓋。那么對于直線段上任一點，滿足()≥，?∈, 直線段被稱為布站線。此時所有穿越直線段的目標均可以被多基地雷達網絡探測到。不失一般性，在直線段上從左到右依次部署發射器和接收器。同時，為了充分發揮發射器的作用，布站線的左右兩端均部署接收器，如圖3所示。

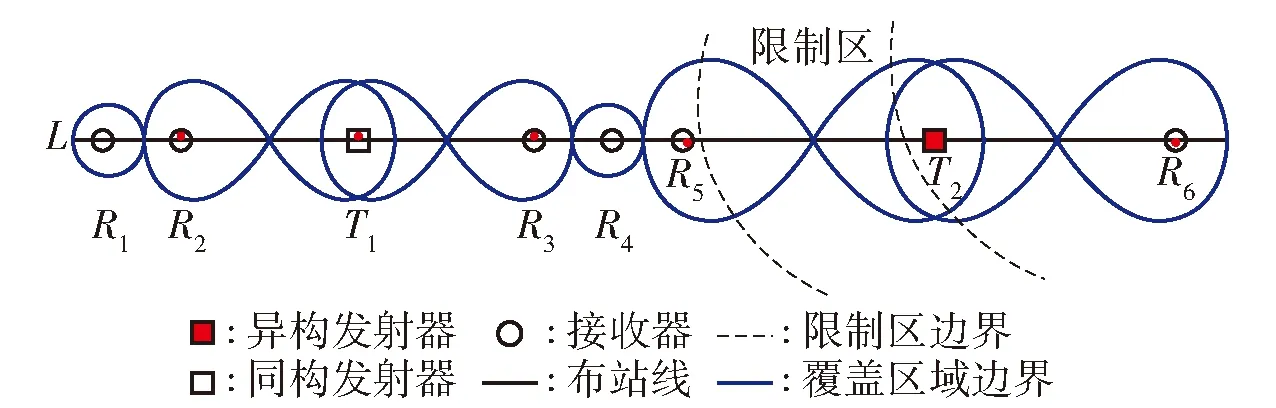
圖3 HMMR直線柵欄覆蓋示意圖Fig.3 HMMR linear barrier coverage diagram

圖4 模式中發射器耦合度(Tj>Ti)Fig.4 Transmitter coupling degree of

1.3 直線柵欄覆蓋問題描述

圖5中，布站線左端點為數軸的原點，布站限制區寬度‖‖=，限制區將布站線分為和兩段，長度分別記為、。

圖5 布站線示意圖Fig.5 Deployment diagram

因此問題可表述為：在有約束的布站線上采用1個異構發射器和若干同構發射器及接收器構建直線柵欄覆蓋，上任意一點均處于雷達網絡的覆蓋范圍內。在總布站成本最小的準則下優化布站節點的位置和數量。相應的模型為

min++
s.t.()≥,?∈,=+
=,,?(,),=1,…,

(3)

2 最優柵欄覆蓋序列的特征與優化模型

2.1 基本模式覆蓋長度的計算及性質

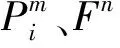
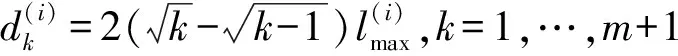
(4)

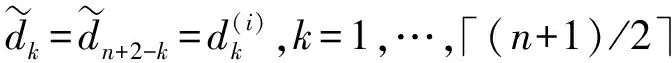
(5)

式中：「?表示向上取整。

以下進一步給出柵欄覆蓋長度的計算公式及主要證明過程。

211 覆蓋長度計算公式

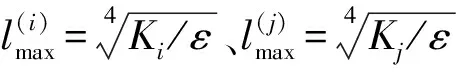
(6)

(7)

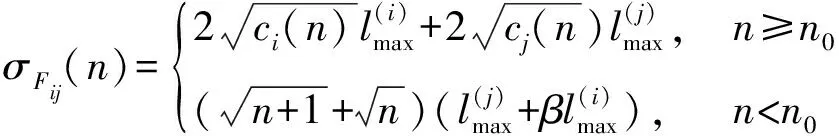
(8)

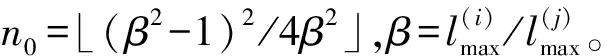
結論1和結論2可通過簡單的代數運算證明，過程從略。

進一步，構建HTMR覆蓋長度增幅序列{|=(+1)-()}，由(8)式可以證明該序列具有單調遞減性。該特點說明隨著接收器數量增加，HTMR覆蓋長度也會增加，但是增加的幅度是遞減的。因此僅通過增加接收器來增加覆蓋長度的方法不是最優的。同理可構造HMMR覆蓋長度序列{|=(+1)-()}，該序列也是單調遞減序列，即通過增加接收器來增加HMMR覆蓋長度的方法也不是最優的。因此需要研究覆蓋長度的性質，確定最優布站方法。

212 HMMR模式的性質

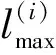
設,為自然數，如下結論成立：

1)若+=2,則當且僅當=，或、均為連續奇數時，()+()取得最大值2()；

2)若+=2+1，則當且僅當|-|=1時，()+()取得最大值()+(+1)。

1) 不妨令=-，=+,為非負整數。當、均為奇數時，分為奇數和偶數2種情況進行證明。

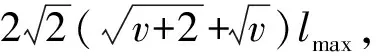
②若為奇數，則為偶數，類似可證明當且僅當=0，即、均為相等奇數時取得最大值。

在、均為偶數時，也分為奇數和偶數2種情況進行證明。

其余情況可類似證得結論1成立。

2) 不妨令=+1-,=+，為偶數，為奇數。類似結論1的證明，可得結論2成立。由定理2可知(2+1)+(2-1)=2(2),這表明兩個同構模式2-1與2+1覆蓋長度之和可用2個相同的模式2等量替代。另一方面，模式2與2+2的覆蓋和不可用2個模式2+1替代，即(2)+(2+2)<2(2+1)。

設、為自然數， 若+為定值，那么，當且僅當|-2|≤1時，()+()的值最大。進一步有，當為奇數時，=(-1)2或=(+1)2；當為偶數時，=2。

分3種情況進行證明：①+=3+2;②+=3+1;③+=3。下面給出當+=3+2時的證明過程，不妨令=2+1-,=+1+，則

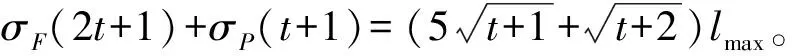
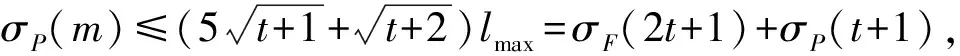
同理可證，若+=3，則當且僅當=2，=時，()+()取最大值(2)+(),即=2。若+=3+1，則當且僅當=、=2+1時，()+()取最大值(2+1)+()，即=(-1)2。

定理2和3說明了HMMR中最優柵欄覆蓋序列的性質，以下研究HTMR中最優覆蓋序列性質。

213 HTMR模式的性質

(′)+(′)≤()+()

(9)

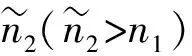
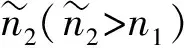
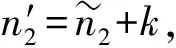
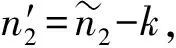
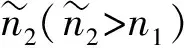
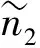
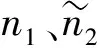
214 最優柵欄覆蓋序列的基本結構

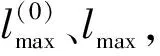
2.2 布站問題的優化模型及其求解算法

模型M：

(10)

模型M的目標函數中沒有顯含變量Δ，但目標函數值的大小卻依賴于Δ。直接求解十分困難，因此本文提出分層分解的算法：第1層，模型M拆分為模型M-1、模型M-2及模型M-3；第2層，模型M-1,M-2再分別按照模型M-1-1、M-1-2拆分。

模型M-1:

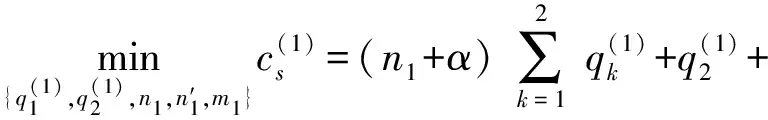
式中:

(11)

模型M-2:

式中:

(12)

再求解以下優化模型：

模型M-3:

(13)

由于優化模型(11)式與優化模型(12)式的求解算法類似，下面以求解模型(11)式為例給出具體算法。

首先對給定的進一步分解模型M-1，則有

模型M-1-1：

min{q(1)1,q(1)2,n′1,t(1)1,t(1)2}cn1=q(1)1(n1+α)+t(1)1n12+n1+q(1)2(n1+1+α)+t(1)2n1+12+αs.t. q(1)1σF(n1)+q(1)2σF(n1+1)+σF10(n′1)+t(1)1σP(n12)+t(1)2σP(n1+12)≥ξs1

(14)

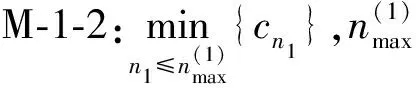
由此可得模型(11)式的最優解。綜上，本文模型分解過程如圖6所示，相應的算法流程如圖7所示。

圖6 模型分解過程Fig.6 Model decomposition

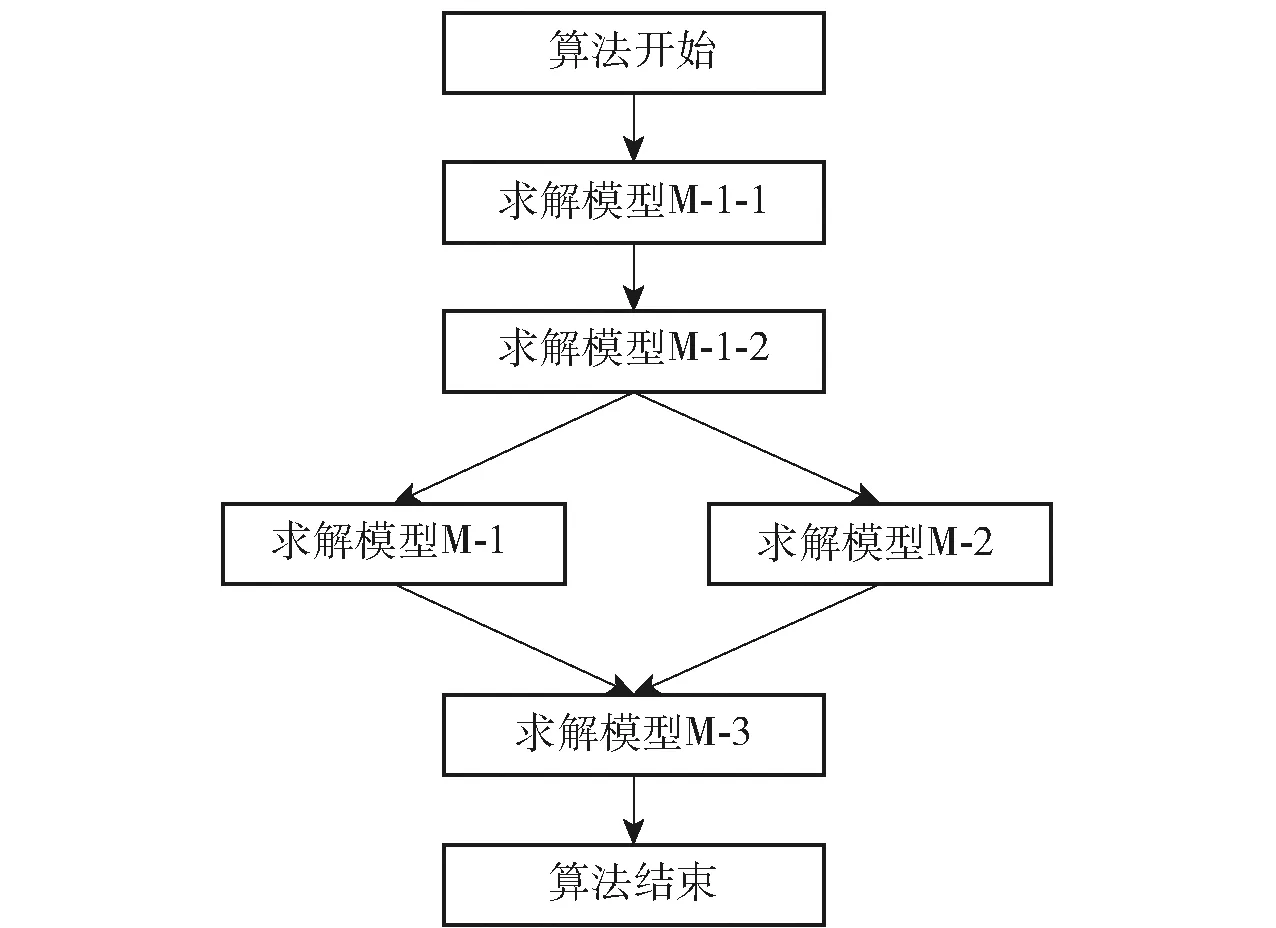
圖7 算法流程圖Fig.7 Algorithm workflow

=?(-1)2」

(15)

具體算法步驟如圖8所示。

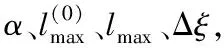
3： 對求解子優化問題(14)，得到HMMR模式中接收器個數為時，直線最優覆蓋序列

優化模型(13)式的求解算法如圖9所示。

3 仿真實驗與結果分析

本節通過仿真實驗來說明所提方法的有效性與可行性。假設柵欄的長度從100 km以步長20 km增加到300 km，限制區的寬度為3 km，且其左右兩邊的布站線長度分別為=67+10和=30+10,=0,…,10。不失一般性，設接收器的費用=1元，在算法2中設置步長為01 km。其他參數設置如表1所示。

表1 仿真試驗參數設置

方案1柵欄長度與布站費用關系如圖10所示。由圖10可以看出，總費用隨著柵欄長度的增加而增加，且呈現近似線性關系。發射器的費用總是大于

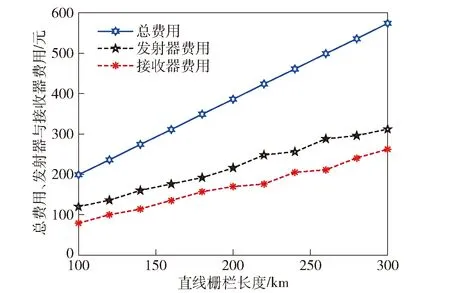
圖10 方案1柵欄長度與布站費用關系Fig.10 Barrier length versus deployment cost for Scheme 1

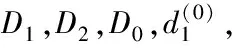
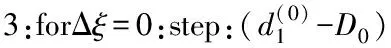
4： 初始化集合=?

5： for=1∶2

6：=()+Δ，=-

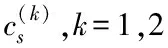
接收器的費用，若發射器費用增加幅度大，相應地接收器費用增加幅度就小，反之亦然。

方案1柵欄長度與傳感器數量關系如圖11所示。由圖11可以看出，布站所用總節點數量、接收器數量和發射器數量隨柵欄長度增加的變化趨勢。總節點數量與接收器數量的變化趨勢一致，且變化幅度較大，而發射器數量的變化趨勢平緩，呈近似線性變化。這是因為發射器的費用要遠大于接收器的費用，為了使布站費用最小，盡可能多用較低費用的接收器而少用發射器。當然也不能僅通過增加接收器，定理1指出隨著接收器數量的增加，其覆蓋效果就越差，因此，需要優化使用發射器與接收器才能使布站費用最少。

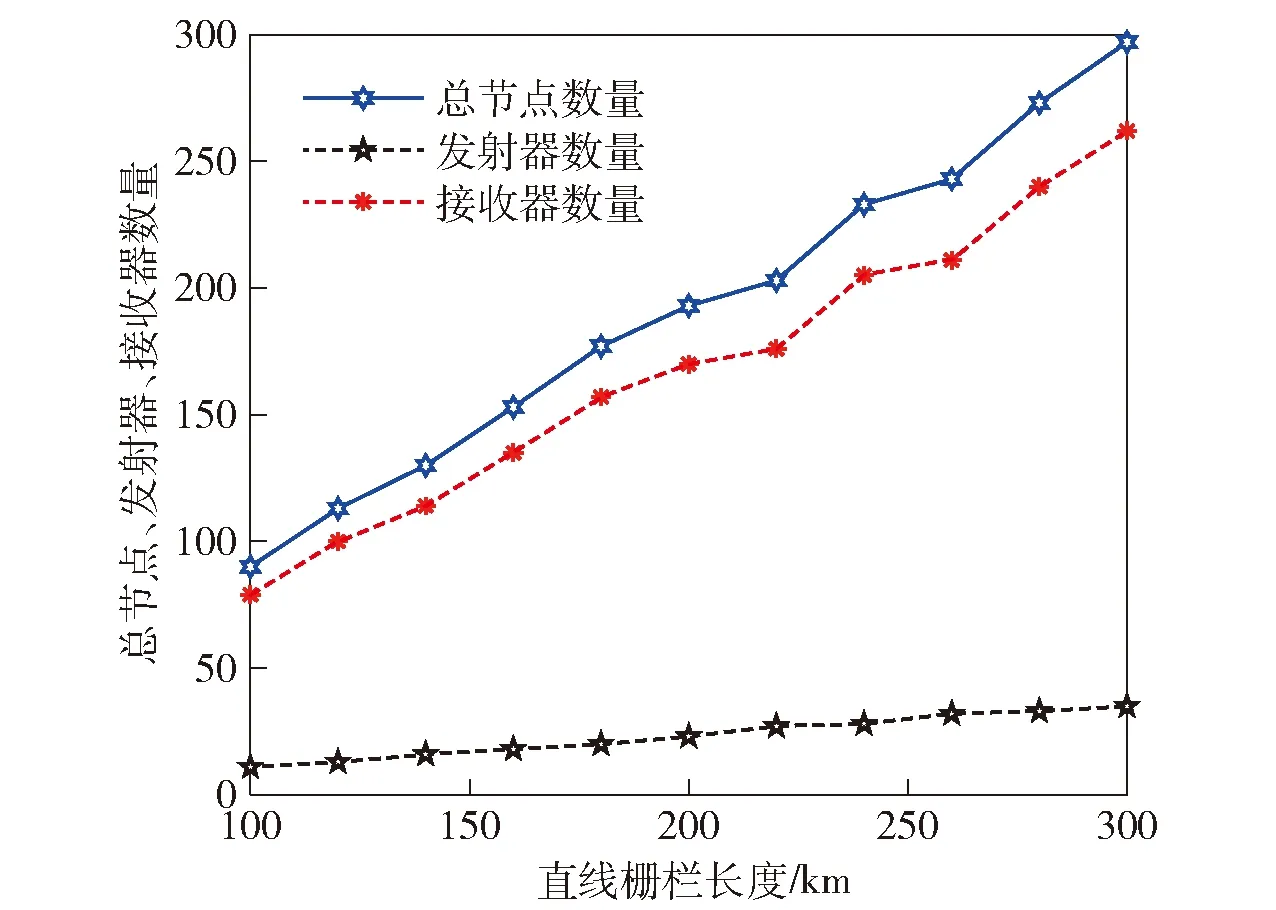
圖11 方案1柵欄長度與傳感器數量關系Fig.11 Barrier length versus number of sensors for Scheme 1

下面對方案2與方案1的優化結果進行比較。在方案2中，HTMR模式中發射器性能不變，而其余同構雷達發射器的性能增強。相應的布站總費用、發射器、接收器費用差如圖12所示(方案1費用減方案2的相關費用)。

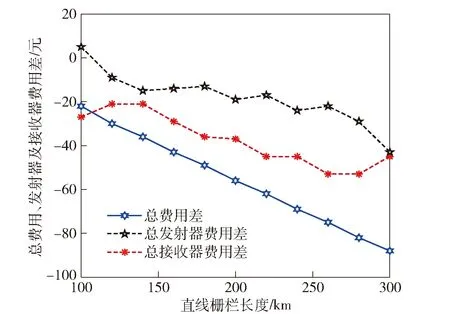
圖12 方案1與方案2費用差Fig.12 Cost difference between Scheme 1 and Scheme 2

圖12表明，與方案2相比，方案1消耗的總費用、接收器費用和發射器費用普遍較少。這是由于方案2中HMMR發射器的成本更高，因此在方案2中更多使用了成本較低的接收器，少用了成本高的發射器，但是方案2中發射器的費用仍高于方案1發射器的費用。

方案3與方案1優化結果的比較。在方案3中，發射器的性能增強，而其余發射器性能不變，相應的布站總費用、發射器、接收器費用差如圖13所示(方案1費用減去方案3的相關費用)。

圖13 方案1與方案3費用差示圖Fig.13 Cost difference between Scheme 1 and Scheme 3

由圖13可知，方案1比方案3節省費用，但節省的數量不大，且不隨柵欄的長度變化而改變。這是由于兩個方案的差別僅在于一個異構的發射器，方案3中異構雷達發射器的探測性能增強了，而其余的發射器探測性能相同。發射器費用及接收器費用隨著柵欄長度的改變而變化，但二者呈現出此消彼長的趨勢。

在仿真實驗中，假設雷達的探測閾值與雷達的費用為近似線性關系，在實際應用中可根據實際情況進行調整。

仿真實驗表明，布站總費會隨采取的布站方案不同而改變。因此在有多種雷達可選擇的條件下，參考本文方法進行仿真，有助于選擇最經濟的布站方案。

下面以柵欄長度=180 km(其中限制區寬度等于3 km，=107 km，=70 km)為例給出以上 3種方案的具體布站序列。

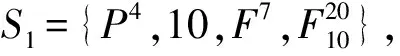
4 結論

本文在雷達布站位置受限的情況下，討論了一種直線柵欄覆蓋的優化布站方法。本文假設當有一對雷達的布站位置受限制的情況，在尋找兩個柵欄覆蓋分界點(即發射器的布站位置)時，由于是在一維區間，故采用定步長的一維搜索方法。從本文的仿真結果看出，利用本文所提方法，在實際應用中可以準備多種不同的雷達布站方案，從中選擇成本最小的方案作為最終的布站結果。最優的柵欄覆蓋布站方法往往與實際場景密切相關，如無法構建直線柵欄覆蓋，而用若干段直線構成的折線柵欄覆蓋；或跨越多條河流的直線柵欄等等。本文所構建的數學模型與布站方法可以拓展到這些雷達布站位置受限制的情況，此時優化模型的復雜度增大，相應求解算法的難度會顯著增大，這種情況下，定步長搜索方法效率低，需要采用其他的優化算法進行求解，如智能算法中的遺傳算法、蟻群算法、鯨魚優化算法、哈里斯鷹優化算法等等。