結構保持圖拉普拉斯正則的快速圖像修復

曾勛勛，陳飛

(1.福州大學數學與統計學院，福建 福州 350108;2.福州大學計算機與大數據學院，福建 福州 350108)

0 引言

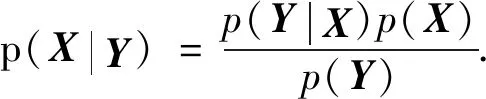
(1)

最近，圖拉普拉斯作為圖像的正則先驗受到極大的關注[16-17]，其假設原始的圖像關于一個給定的圖是分片平滑.這種基于圖的表達跟傳統的方法相比具有更加緊、精確和結構自適應等優點[16].早期圖拉普拉斯正則[18]是采用固定的圖拉普拉斯矩陣提升信號的分片平滑性.之后，考慮到信號的變化對所構建的圖有輔助作用，信號依賴的圖拉普拉斯正則(SDGLR)[17]被提出，其中拉普拉斯矩陣的邊權重的構建是依賴于圖像像素的灰度值差，即拉普拉斯矩陣可以看作是信號的函數.最近，特征圖拉普拉斯正則[19]被提出并應用于提升點云數據的分片平滑性質.對于圖像修復，梯度有助于結構保持，可以促進待修復區域與周圍圖像信息的一致性.然而，如何有效將梯度特征融合至圖拉普拉斯矩陣是一個關鍵問題.

將梯度作為圖像結構保持的重要特征，利用圖拉普拉斯矩陣提升梯度域圖像的分片平滑性.首先將圖像看作圖信號，構建圖拉普拉斯矩陣，然后對水平梯度圖像和垂直梯度圖像進行圖拉普拉斯正則，接著圖像修復模型可以轉化為線性方程組，最后通過共軛梯度法快速求解.

1 圖的構建

對于二維圖像X∈RM×N，首先按列排成一維長向量x,x=vec(X)∈RMN×1,其中：vec(·)表示向量化操作算子.接著，定義一個包含MN個節點(圖像像素)的圖，圖中每個節點包含兩個信息：像素位置li和像素的灰度值xi,i∈{1,2,…,MN}.wi,j表示節點i和節點j之間的邊權重,其定義用高斯核函數表示為：

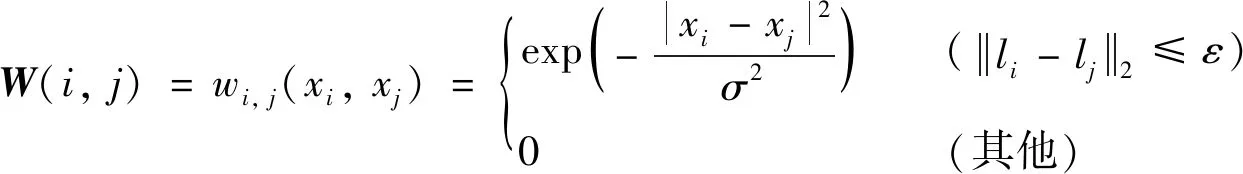
(2)

(3)

2 結構保持圖拉普拉斯正則

對于圖像修復來說，利用周圍信息向待修復區域傳播時，通過引入圖像梯度信息，保持圖像結構特征是一種有效方法.給定二維圖像X∈RM×N，其水平梯度圖像和垂直梯度圖像可通過逐行和逐列計算得到.為了使得到的水平梯度圖像與垂直梯度圖像維數一致，將邊界梯度值置0.以水平梯度圖像為例，對于任意k∈{1,2,…,M},l∈{1,2,…,N-1}，定義Gh(k,l)=X(k,l+1)-X(k,l)且Gh(k,N)=0.那么水平梯度圖像Gh∈RM×N可以轉換為一維形式，gh=vec(Gh)∈RMN×1，其矩陣表達方式為：gh=Fhx.其中：Fh∈RMN×MN為水平梯度算子.類似地，對任意l∈{1,2,…,N}，垂直方向的梯度圖像定義為：Gv(k,l)=X(k+1,l)-X(k,l),k∈{1,2,…,M-1}且Gv(M,l)=0,那么，有：gv=Fvx.其中，Fv∈RMN×MN為垂直梯度算子.

對于圖像X，在點(k,l)處的梯度(Gh(k,l),Gv(k,l))指明了圖像灰度值最大的增長方向.如果點(k,l)處在圖像的邊緣位置，那么其切線方向將近似垂直于該點的梯度方向(見圖1).因此在周圍已知區域向待修復區域信息傳播的過程中，通過梯度方向保持一致可以保護圖像的邊緣結構.為了提升梯度域圖像的近似分片平滑性，對圖像X的水平梯度圖像Gh和垂直梯度圖像Gv，提出結構保持的圖拉普拉斯正則項：

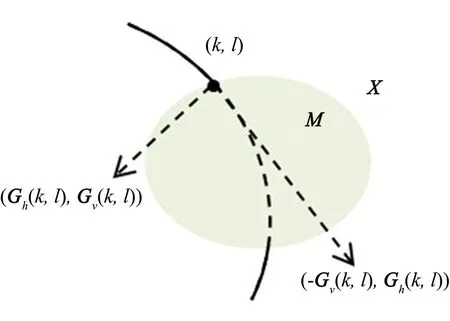
圖1 圖像X上邊緣點(k,l)處梯度方向Fig.1 The gradient direction of edge point(k,l) on image X

(4)

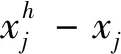
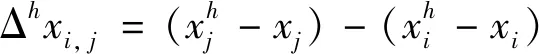
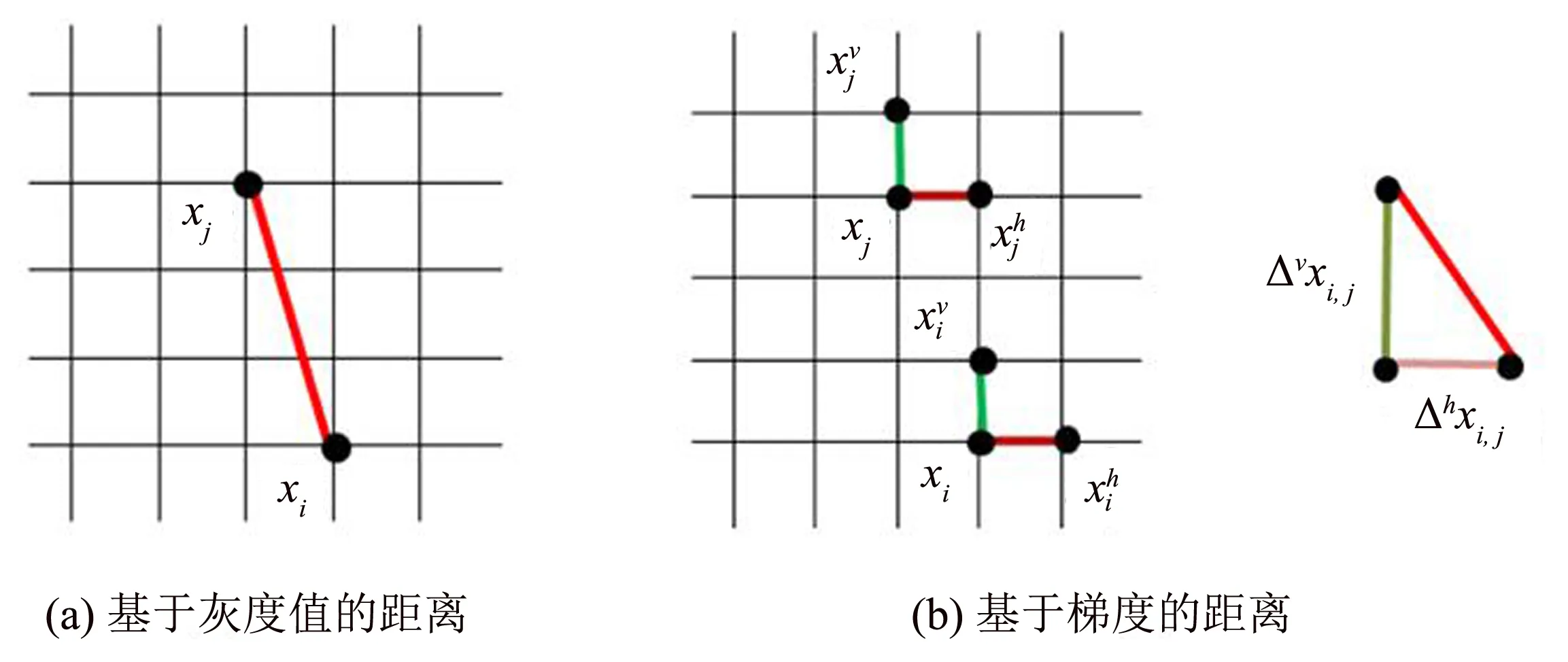
圖2 兩種距離的比較說明Fig.2 Comparison illustration of two distances

接下來，從連續域上證明任何分片平面圖像f是正則函數Φ的全局最小值.假設Ω是圖像支撐域,Ωi(i=1,2,…,T)是Ω的一個劃分.那么，分片平面圖像可以定義為：

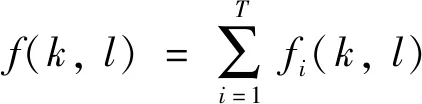
(5)

其中，

(6)

這里，組合圖像f(k,l)是連續的.注意到任何兩個連接的fi(k,l)和fj(k,l)必須在不同平面上，否則可以合并為一個平面.定義?Ωi為劃分區域Ωi的邊緣，那么Ωi-?Ωi是Ωi的內部.顯然有

?fi(k,l)=常數 ((k,l)∈(Ωi-?Ωi))

(7)

那么，對于i=1,2,…,T,有：

?2fi(k,l)=0 ((k,l)∈(Ωi-?Ωi))

(8)

則可以得到：

?2f(k,l)=0 ((k,l)∈(Ω-?Ω))

(9)

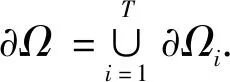
對于任意兩個相鄰的不同平面fi和fj上，由于梯度在邊界?Ω處是不連續的，故?fi≠?fj.因此，?2f(k,l)=∞,(k,l)∈?Ω.如果權函數w(k,l)是通過高斯核函數計算得到，那么有w(k,l)=exp(-∞)=0.所以，下式成立.有：

w(k,l)(?fi(k,l)-?fj(k,l))=0 (?(k,l)∈Ω)

(10)

因此，分片平面圖像滿足：

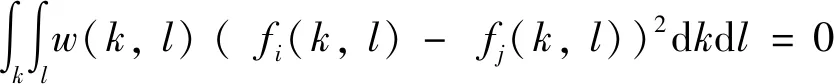
(11)

那么，Φ(f)=0.對于一個分片平面圖像x及其圖定義權重wi,j，在不同平面的交界處wi,j≈0，有

(12)

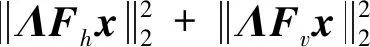
3 圖像修復

給定一張退化的一維圖像y∈RMN×1，引入結構保持的圖拉普拉斯正則項式(4)，從中恢復潛在的真實圖像x，可以用模型表示為：

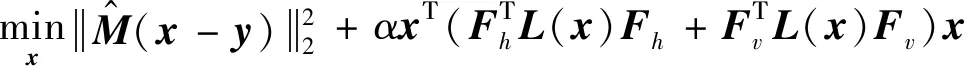
(13)

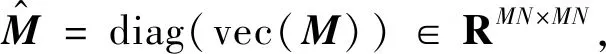
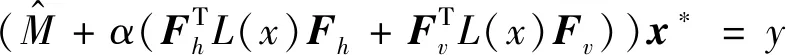
(14)

為了評價所提出算法的圖像復原效果，定理1給出了圖像修復誤差上界，說明了該上界與矩陣Γ的特征值緊密相關.針對分片平面圖像x，與傳統的拉普拉斯矩陣相比，定理2給出了特征值之間的關系，從而保證所提出的解與圖拉普拉斯正則得到的解相比可以得到更小的上界.

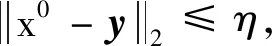
(15)

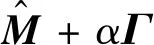
證畢.

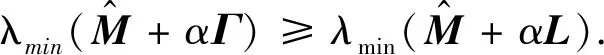
證明 假設ρ(xi)是xi所在的平面，wi,j是指用相同的高斯核函數定義的xi與xj相似性權重，那么有：

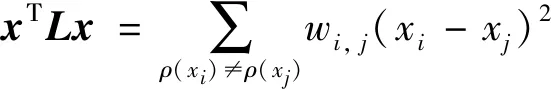
(16)

以4鄰域4連接圖為例，考慮xi與xj所有可能的平面，都有：

因此，Γ≥L.通過Rayleigh引理[20],有：

(17)

證畢.

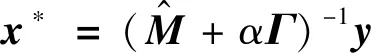
4 實驗結果與分析

本研究算法在設置權重矩陣式(2)時，ε采用4鄰域構建4連接圖，核函數σ設置為0.58.圖像修復算法中正則項參數α設置為0.01.為了評價圖像復原的質量，引入PSNR (峰值信噪比)和SSIM(結構相似性)作為衡量指標：

為了驗證所提出的算法，首先與圖拉普拉斯正則(SDGLR)[17]做比較.圖3給出了兩組實驗結果，SDGLR容易過于平滑，且與周圍的紋理不一致，塊狀明顯.本研究提出的結構保持圖拉普拉斯正則化方法，可以更好地保持圖像紋理信息，使得修復后的圖像更加自然.

圖3 視覺與PSNR比較Fig.3 Visual and PSNR comparison

為了綜合比較所提出的結構保持圖拉普拉斯正則器，比較了當前主流的圖像修復算法，包括SDGLR、EPLL[22]、CSC[3]、IRCNN[23]、IDBP[2]、GSC[24].注意到IRCNN是基于深度學習的方法.以12張常見圖像為測試數據[25]，隨機丟失90%以上像素，采用不同方法重建圖像，其修復后的的平均PSNR和SSIM列在表1.

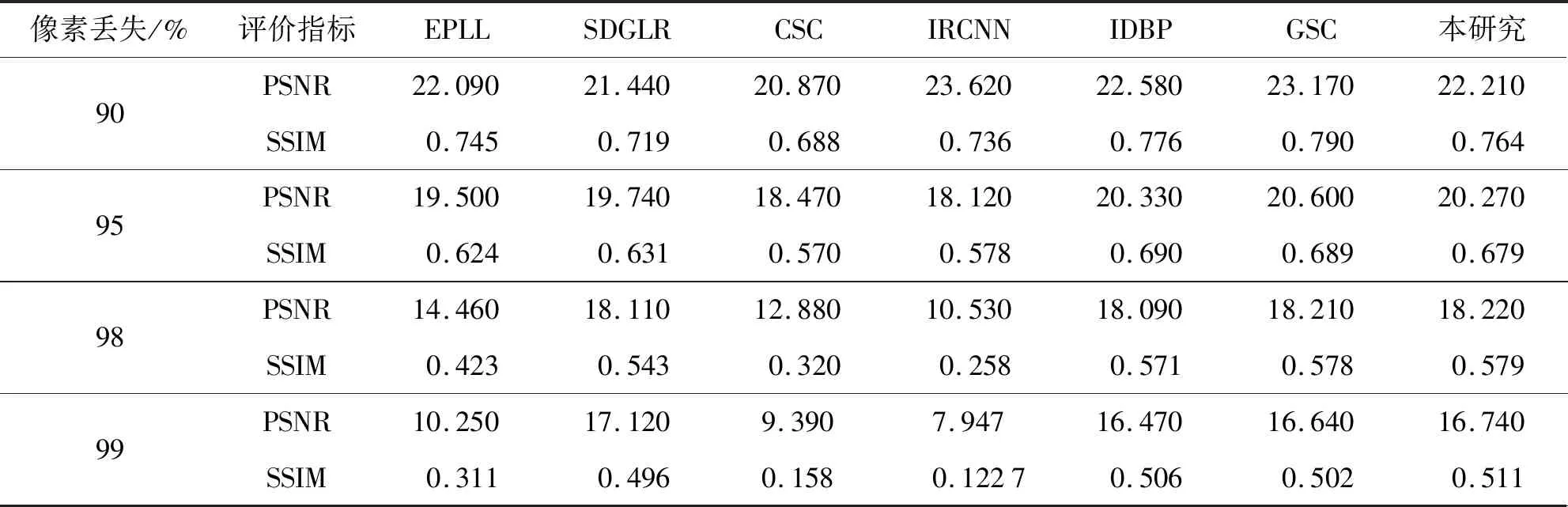
表1 不同方法在12張隨機丟失90%以上像素的圖像上實驗結果比較Tab.1 Comparison by different methods on 12 test images with more than 90% randomly missing pixels

圖4為針對Man圖像隨機丟失90%像素的幾種算法結果比較.可以看到，本研究所提出的算法雖然PSNR不是最高，但是其視覺質量明顯比主流的基于塊學習的算法效果好.特別對于大量丟失像素的圖像，基于深度學習和字典學習的方法，由于其性能強依賴于訓練數據，使得其修復精度不高，局部圖像紋理細節丟失，比如衣服袖子.基于非局部自相似算法，由于部分圖像局部細節不存在明顯的自相似性，因此容易造成過平滑或塊效應，且會產生虛假的邊緣結構信息，比如人臉面部.圖5為針對Boat圖像隨機丟失90%像素的幾種算法結果比較.同樣的，本研究算法的視覺質量明顯比主流的基于塊學習的算法效果好，沒有明顯的塊效應和過度平滑現象.表2列出了不同方法針對128 px×128 px圖像的運行時間,其中筆記本電腦配置：Intel Core i5-8365U CPU 1.60 GHz，所有實驗都運行在Matlab 2015b上.實驗結果表明所提出的圖像修復算法相比于現有圖像修復算法速度提升6倍左右.

圖4 Man圖像的幾種算法結果比較Fig.4 Comparison by different methods on the Man image

圖5 Boat圖像的幾種算法結果比較.Fig.5 Comparison by different methods on the image

表2 幾種算法在128 px×128 px圖像上平均運行時間Tab.2 Average run time (in sec) on 128 px×128 px images (s)

5 結語

提出一種基于結構保持圖拉普拉斯正則的圖像修復算法.相比于傳統的二階圖拉普拉斯正則化算法，引入梯度信息實現結構保持，使周圍信息沿著圖像梯度的法方向延伸至待修復區域，從而達到圖像修復的目的.修復模型可以轉化為線性方程組，并通過共軛梯度法實現快速求解，對于一張128 px×128 px的圖像處理時間不到2 s.通過重建誤差分析，對于分片平面圖像，所提出的算法具有更小的誤差下界.從結果上視覺比較，重建的圖像沒有明顯的塊效應，更加自然.