六自由度工業(yè)機(jī)器人運(yùn)動(dòng)學(xué)分析與仿真

李雪梅，崔菲菲，駱海濤，李 喆

（1.桂林電子科技大學(xué) 機(jī)電工程學(xué)院，桂林 541004；2.中國科學(xué)院沈陽自動(dòng)化研究所，沈陽 110016）

0 引言

隨著制造業(yè)的日益發(fā)展與進(jìn)步，各行各業(yè)對(duì)產(chǎn)品的質(zhì)量和生產(chǎn)效率的要求也在不斷提高，然而人工作業(yè)很難滿足工業(yè)發(fā)展的需求[1]。為了解決這一問題，許多行業(yè)開始使用機(jī)器人代替人工作業(yè)，從而促使工業(yè)機(jī)器人的需求量越來越大。同時(shí)，對(duì)機(jī)器人的控制精度、穩(wěn)定性以及生產(chǎn)效率的要求也在不斷提高[2]，而機(jī)器人運(yùn)動(dòng)學(xué)分析是實(shí)現(xiàn)機(jī)器人運(yùn)動(dòng)控制與軌跡規(guī)劃，提高機(jī)器人控制精度、穩(wěn)定性以和生產(chǎn)效率的基礎(chǔ)[3]。

機(jī)器人的所有操作動(dòng)作都靠其關(guān)節(jié)變化來實(shí)現(xiàn)，關(guān)節(jié)數(shù)越多其靈活性越高，越能完成較復(fù)雜的動(dòng)作[4]。目前使用最為廣泛的是6自由度工業(yè)器人，該類型機(jī)器人的運(yùn)動(dòng)學(xué)分析相對(duì)復(fù)雜。因此，對(duì)6自由度機(jī)器人的運(yùn)動(dòng)學(xué)進(jìn)行研究很有必要。

1 機(jī)器人運(yùn)動(dòng)學(xué)分析

1.1 基于D-H參數(shù)法的機(jī)器人模型

以EFORT機(jī)器人作為分析模型，該模型是一個(gè)開式運(yùn)動(dòng)鏈機(jī)器人。它由7個(gè)連桿通過6個(gè)旋轉(zhuǎn)關(guān)節(jié)串聯(lián)而成，可以在工作空間以不同的方式運(yùn)動(dòng)。采用Denavit與Hartenberg兩位科學(xué)家提出的D-H參數(shù)法來描述連桿和關(guān)節(jié)的幾何關(guān)系。由于連桿0是機(jī)器人的基座，連桿6連接著末端執(zhí)行器。因此，在機(jī)座處建立基坐標(biāo)系{0}，在連桿6處建立工具坐標(biāo)系{6}，其他坐標(biāo)系分別建在余下的各個(gè)關(guān)節(jié)處[5]，如圖1所示。

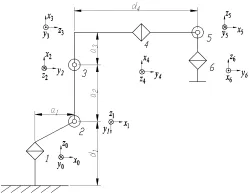
圖1 機(jī)器人的D-H空間坐標(biāo)系

根據(jù)圖1建立的機(jī)器人連桿坐標(biāo)系，可以獲得EFORT機(jī)器人的D-H參數(shù)表，如表1所示。

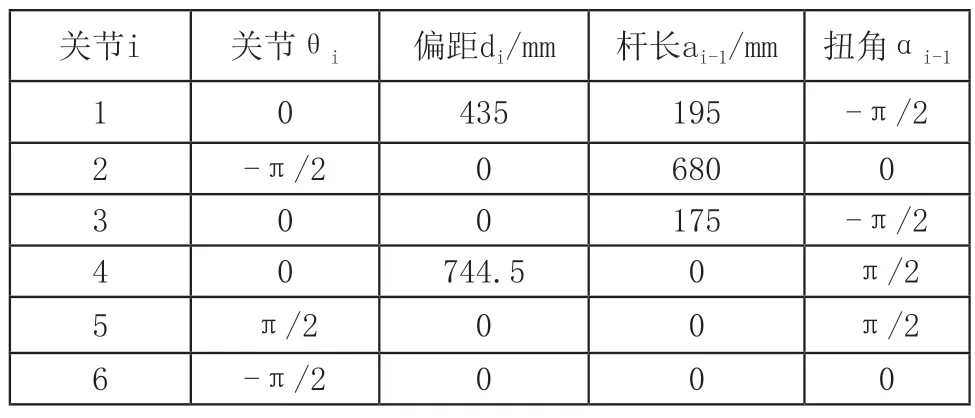
表1 EFORT機(jī)器人參數(shù)

1.2 正運(yùn)動(dòng)學(xué)分析

機(jī)器人正運(yùn)動(dòng)學(xué)分析是在已知機(jī)器人各個(gè)關(guān)節(jié)的轉(zhuǎn)角θi和關(guān)節(jié)偏移di的條件下，通過運(yùn)動(dòng)學(xué)方程求解出機(jī)器人末端執(zhí)行器任意時(shí)刻的位姿[6]。根據(jù)EFORT機(jī)器人坐標(biāo)系和D-H參數(shù)表，可以計(jì)算出相鄰兩個(gè)坐標(biāo)之間的變換矩陣nTn+1(i=1，2，…，6)。即：

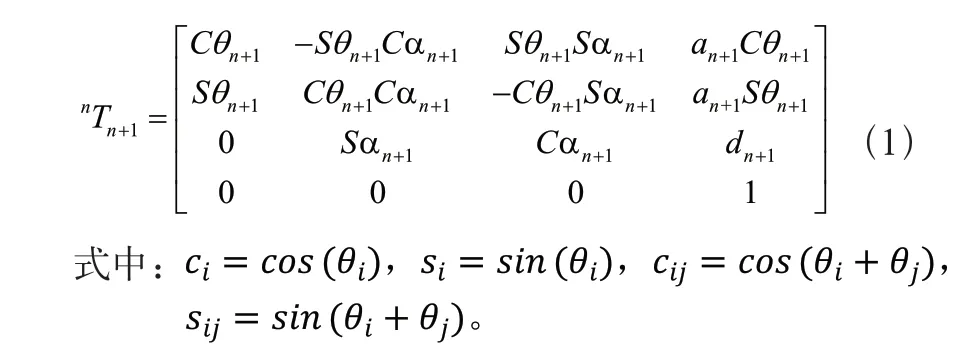
由于該型機(jī)器人含有6個(gè)旋轉(zhuǎn)關(guān)節(jié)，所以存在6個(gè)未知變量，即關(guān)節(jié)角θ1～θ6，將6個(gè)關(guān)節(jié)參數(shù)代入到式(1)中，然后依次相乘，得到六自由度機(jī)器人末端執(zhí)行器相對(duì)基坐標(biāo)系的總變換矩陣：

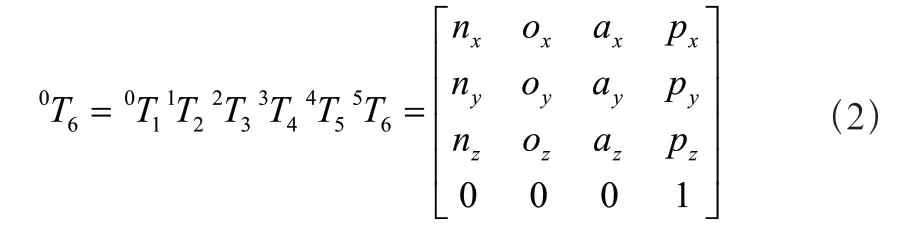
為了檢驗(yàn)機(jī)器人的正運(yùn)動(dòng)學(xué)方程是否正確，將表1中的數(shù)據(jù)代入式(2)中并利用MATLAB計(jì)算，計(jì)算的結(jié)果為：

0T6的左側(cè)3x3矩陣表示機(jī)器人的姿態(tài)，可以發(fā)現(xiàn)：機(jī)器人末端的x軸與基坐標(biāo)系的y軸方向相反，y軸與基坐標(biāo)系的x軸同向，z軸與基坐標(biāo)系的z軸同向。第四列元素代表機(jī)器人末端的位置，可以發(fā)現(xiàn)：機(jī)器人末端位置在基坐標(biāo)系中沿x0軸平移了940mm的距離，沿z0軸平移了1290mm的距離[7]。計(jì)算結(jié)果與圖1所示的工具坐標(biāo)系6的位姿完全相同，表明正運(yùn)動(dòng)學(xué)方程是正確的。

1.3 逆運(yùn)動(dòng)學(xué)分析

機(jī)器人的逆運(yùn)動(dòng)學(xué)分析是在已知機(jī)器人末端執(zhí)行器某一個(gè)期望點(diǎn)位置和姿態(tài)的條件下，求解機(jī)器人6個(gè)旋轉(zhuǎn)關(guān)節(jié)的參數(shù)。由于所研究的EFORT機(jī)器人滿足Piper準(zhǔn)則，所以采用反變換法求解6個(gè)關(guān)節(jié)角度值。由式(1)可以發(fā)現(xiàn)，矩陣中含有三角函數(shù)，為了使角度解耦[8]，可用單個(gè)矩陣的“逆”左乘末端執(zhí)行器的位姿矩陣0T6，于是可求得各關(guān)節(jié)變量θ1～θ6，依次求得結(jié)果如下：

由于在[-180°，180°]區(qū)間內(nèi)，θ1有1個(gè)解，θ2、θ3分別有4個(gè)解，θ4、θ5、θ6分別有8個(gè)解，因此可以得到8組封閉解。

為了檢驗(yàn)?zāi)孢\(yùn)動(dòng)學(xué)算法是否正確，在機(jī)器人的工作空間中任意選取一個(gè)末端點(diǎn)的位姿，其矩陣為：

調(diào)用MATLAB工具箱中的robot.ikine(T)函數(shù)，計(jì)算出各個(gè)連桿的關(guān)節(jié)角為：

q=[0，-1.5708，0.5236，0，1.0472，0]

用時(shí)0.043毫秒。由于機(jī)器人工具箱中自帶的ikine函數(shù)在求解時(shí)會(huì)出現(xiàn)迭代不收斂的情況，從而無法確定每次獲得的任意位姿下機(jī)器人的關(guān)節(jié)角度是否都是準(zhǔn)確的、合理的[9]。因此，用MATLAB編寫出前文用反變換法計(jì)算出的逆解表達(dá)式的相應(yīng)代碼，可求出機(jī)器人的8組封閉解：

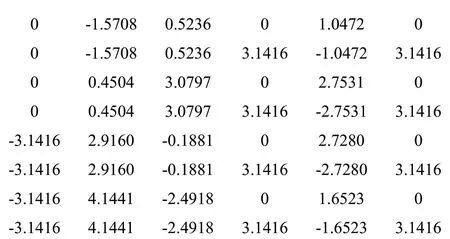
用時(shí)0.006毫秒。將以上8組解分別代回MATLAB的fkine函數(shù)中，均能得到與式(4)相同的結(jié)果，從而對(duì)逆運(yùn)動(dòng)學(xué)算法的準(zhǔn)確性進(jìn)行了檢驗(yàn)。

2 運(yùn)動(dòng)學(xué)仿真

為了更直觀地觀察機(jī)器人在工作空間中的運(yùn)動(dòng)狀態(tài)，采用MATLAB軟件對(duì)其進(jìn)行運(yùn)動(dòng)學(xué)仿真。利用MATLAB Robotics Toolbox中的Link和robot函數(shù)對(duì)機(jī)器人的初始位姿進(jìn)行建模。相關(guān)程序如下：

建立的模型如圖2所示。

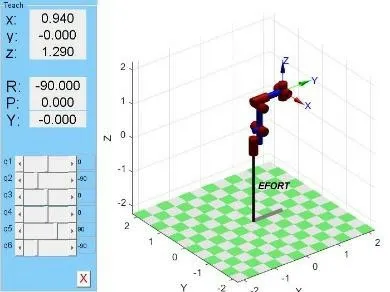
圖2 機(jī)器人三維結(jié)構(gòu)圖

圖2顯示，將初始值（0，-pi/2，0，0，pi/2，-pi/2）分別輸入到q1～q6中，可以得到機(jī)器人末端的位姿，與圖1所示位姿相同，進(jìn)一步檢驗(yàn)了正運(yùn)動(dòng)學(xué)的正確性。也可以通過拖動(dòng)q1～q6的值來觀察機(jī)器人在空間中的運(yùn)動(dòng)情況，方便實(shí)時(shí)模擬仿真。

3 機(jī)器人工作空間分析

當(dāng)機(jī)器人的所有關(guān)節(jié)進(jìn)行所有可能的運(yùn)動(dòng)時(shí)，機(jī)器人末端執(zhí)行器所能達(dá)到的所有點(diǎn)的集合稱為機(jī)器人的工作空間。對(duì)機(jī)器人的工作空間進(jìn)行分析，常用的方法是蒙特卡羅法，該法是通過隨機(jī)抽樣來使機(jī)器人的關(guān)節(jié)取值多樣化，以便在笛卡爾空間中獲得大量的末端點(diǎn)，進(jìn)而可獲得機(jī)器人工作空間的形狀。該法求解步驟如下：

1）由機(jī)器人的正運(yùn)動(dòng)學(xué)方程，可以求解到機(jī)器人末端參考點(diǎn)在笛卡爾坐標(biāo)系中的位置向量為：

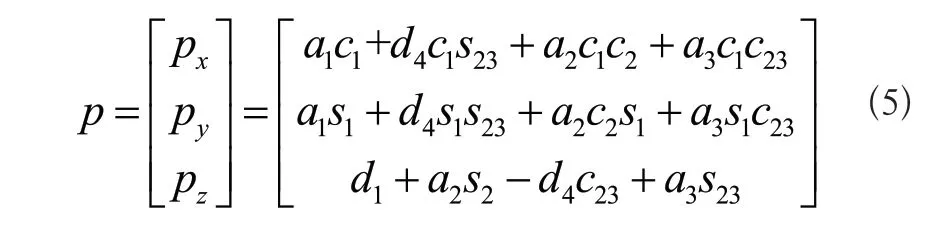
2）使用MATLAB中的RAND函數(shù)，可以在0～1范圍內(nèi)得到一組偽隨機(jī)數(shù)，得到各個(gè)關(guān)節(jié)變量的隨機(jī)值：

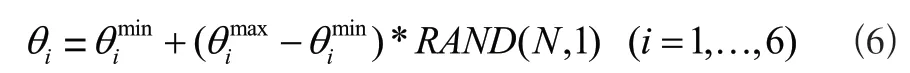
其中：θimax、θimin分別表示關(guān)節(jié)i運(yùn)動(dòng)轉(zhuǎn)角范圍的最大、小值；N為迭代次數(shù)，這里N取值為20000。

3）將機(jī)器人各關(guān)節(jié)變量隨機(jī)生成的N個(gè)隨機(jī)數(shù)代入末端執(zhí)行器位置向量[px，py，pz]T中，可得機(jī)器人末端執(zhí)行器在笛卡爾空間中的位置坐標(biāo)。

4）借助MATLAB中的plot3函數(shù)繪制出機(jī)器人末端的工作空間點(diǎn)狀云圖，如圖3所示。

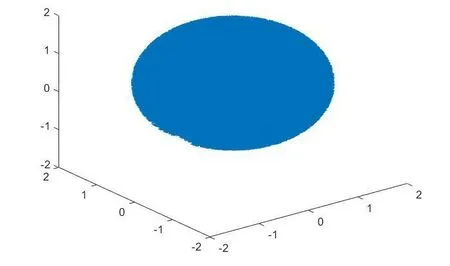
圖3 三維工作空間

圖4、圖5分別為空間點(diǎn)云圖在xoy二維平面和xoz二維平面上的投影。機(jī)器人的三維空間隨機(jī)位置點(diǎn)數(shù)量足夠的多，獲得的空間的精確度就越高，空間輪廓也越清晰。

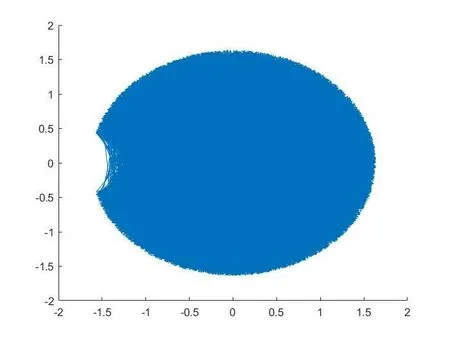
圖4 XOY平面投影

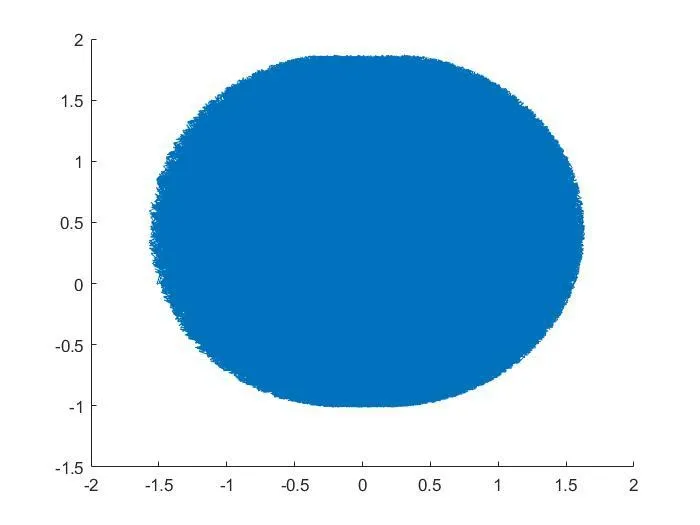
圖5 XOZ平面投影

通過分析機(jī)器人的工作空間點(diǎn)云圖可以發(fā)現(xiàn)，機(jī)器人的工作空間沒有出現(xiàn)空腔和空洞，說明機(jī)器人整體上滿足作業(yè)要求[10]。

4 機(jī)器人的可操作性分析

機(jī)器人的可操作性是一個(gè)相對(duì)重要的技術(shù)指標(biāo)，它關(guān)系到機(jī)器人在工作過程中與操作目標(biāo)之間的協(xié)調(diào)性，這對(duì)于提高生產(chǎn)效率及生產(chǎn)安全性都至關(guān)重要[11]。

分析機(jī)器人的可操作性，一般用雅克比矩陣J(q)的行列式是否為0來判別機(jī)器人是否處于奇異位置，用雅克比矩陣的奇異性來描述機(jī)器人的靈巧性[12]。速度可操縱性橢球體可以表示機(jī)器人任意改變末端執(zhí)行器位置和方向的能力。

末端執(zhí)行器速度空間橢球體方程為：

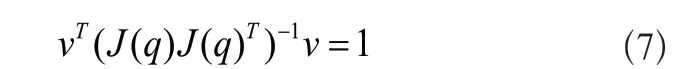
式(J(q)J(q)T)-1指工作空間中的某個(gè)橢球，也叫作機(jī)器人操作度橢球。末端執(zhí)行器可以以較高的速度沿著橢球的主軸方向運(yùn)動(dòng)，而以較慢的速度在副軸上運(yùn)動(dòng)。如果該橢球的形狀近似于球形，即它所有的半徑均在同一數(shù)量級(jí)，那么機(jī)器人末端可以達(dá)到任意的笛卡爾速度。如果其中一個(gè)或多個(gè)半徑相對(duì)較小，表明機(jī)器人末端不能達(dá)到那些小半徑所對(duì)應(yīng)的速度。

當(dāng)關(guān)節(jié)角為[0，-π/2，-π/2，0，π/6，-π/2]時(shí)，機(jī)器人是奇異的。然后用MATLAB 中的plot_ellipse(J*J’)函數(shù)繪制出末端執(zhí)行器平移速度橢球，如圖6所示，可以發(fā)現(xiàn)，末端執(zhí)行器的平移速度橢球近似于一個(gè)厚度幾乎為零的厚板。這表明機(jī)器人不能繞小半徑對(duì)應(yīng)的方向旋轉(zhuǎn)，同時(shí)用MATLAB工具箱中的maniplty函數(shù)計(jì)算出此狀態(tài)下的機(jī)器人可操作度為0。

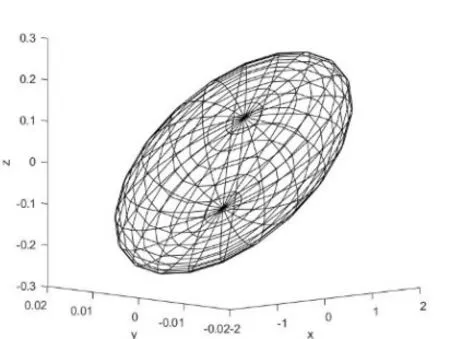
圖6 機(jī)器人末端平移速度橢球

當(dāng)機(jī)器人處于標(biāo)準(zhǔn)位置時(shí)，末端執(zhí)行器的旋轉(zhuǎn)速度橢球如圖7所示。由圖7可以看出：機(jī)器人末端執(zhí)行器旋轉(zhuǎn)速度橢球近似于一個(gè)球體，所以末端執(zhí)行器可以在y軸和z軸方向?qū)崿F(xiàn)比x軸方向更高的速度，機(jī)器人的可操作度大一些。此時(shí)機(jī)器人旋轉(zhuǎn)操作度為0.475631，平移操作度為2.44949。

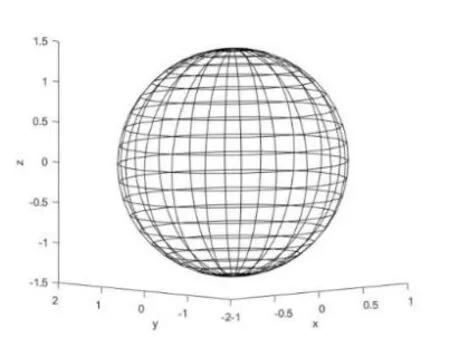
圖7 機(jī)器人末端旋轉(zhuǎn)速度橢球

5 結(jié)語

以EFORT機(jī)器人作為研究目標(biāo)，采用D-H方法完成了6R機(jī)器人的運(yùn)動(dòng)學(xué)分析。通過兩個(gè)相鄰連桿之間的變換矩陣順次相乘得到末端執(zhí)行器的位姿矩陣。根據(jù)反變換法求解出機(jī)器人的8組封閉解，并運(yùn)用MATLAB軟件檢驗(yàn)了其正、逆運(yùn)動(dòng)學(xué)方程的準(zhǔn)確性和合理性。結(jié)果表明：用反變換編寫的函數(shù)求解速度要快于工具箱自帶函數(shù)求解速度。其次，依據(jù)蒙特卡羅法分析了機(jī)器人的工作空間，結(jié)果顯示，所得到的點(diǎn)云圖均勻且并不存在空腔等問題。最后，利用雅克比矩陣函數(shù)，分析了機(jī)器人的靈活性，結(jié)果表明機(jī)器人具有良好的可操作性。