繩牽引并聯機構末端執行器運動軌跡規劃

侯澤群，楊 芳,2，薛玉君,2,3，李 航,2，彭 程

1河南科技大學機電工程學院 河南洛陽 471003

2河南省機械設計及傳動系統重點實驗室 河南洛陽 471003

3礦山重型裝備國家重點實驗室 河南洛陽 471039

并聯機構具有累計誤差小、運動精度高、動態性能好等特點，被廣泛應用在重型機械、機器人和智能裝備等領域[1-2]。繩牽引并聯機構是并聯機構的一個分支，用繩索代替了剛性連桿。繩牽引與剛性連桿相比，由于其質量較輕，極大地減小了運動部件的慣性，因而繩牽引并聯機構在需要高速運動的場合下具有明顯優勢[3]。此外，相對于傳統的剛性連桿并聯機構，繩牽引并聯機構還具有工作空間大、結構簡單、運動速度快等優點[4-5]。繩牽引并聯機構具有并聯機構和繩索驅動的共同優勢，使得繩牽引并聯機構一直是相關領域研究熱點，受到越來越多的關注[6-8]。

為了獲得較高的末端軌跡運動性能，需要對運動軌跡進行規劃。Jiang 等人[9]針對六自由度繩牽引并聯機構的點對點軌跡規劃問題，利用球面線性插值法使線段之間的平移和旋轉加速度過渡具有連續性。Gosselin 等人[10]針對兩自由度懸索并聯機器人的點對點軌跡規劃問題，采用多項式插值法和三角函數法進行對比，2 種方法都可以保證加速度的連續性。Xiang等人[11]將懸索并聯機器人建立成線性等效動力學模型，進行了部分解耦，并利用二次規劃的方法實現了軌跡生成。張文佳等人[12]提出了一種 S 型-梯形規劃方法，可以使得起止點和終止點的加速度為零，而中間若干點的加速度不為零，實現軌跡規劃。Yuan 等人[13]采用三次樣條插值法對繩牽引并聯機構進行軌跡規劃并設計試驗，通過試驗表明基于運動學模型的軌跡規劃具有良好的精度。Li 等人[14]對四自由度SCARA 型并聯機器人，利用 5 次 B 樣條曲線生成了光滑的運動軌跡，在試驗結果中獲得了連續平滑的關節力矩，降低了末端執行器的振動。

筆者面向繩牽引并聯機構運動性能需要，開展繩牽引并聯機構的運動軌跡規劃研究。在考慮牽引繩柔性特點的基礎上，結合運動學模型，采用 Adams 和MATLAB 建立聯合仿真模型，來模擬牽引繩的非線性特征。在此基礎上，設計了改進多項式方法來規劃末端執行器的運動軌跡規劃。通過仿真分析與試驗驗證了該軌跡規劃方法的有效性，使末端執行器運動軌跡平滑，有效減少了驅動電動機的啟停次數，為后續開展軌跡運動控制奠定了基礎。

1 繩牽引末端執行器運動學建模

1.1 繩牽引并聯機構

繩牽引并聯機構采用 4 臺直線電動機牽引繩索，進而通過帶動繩索使末端執行器按照規劃的軌跡進行運動，繩牽引末端執行器運動機構如圖 1 所示。初始時，直線電動機動子滑塊都在軌道中間位置，末端執行器中心位于坐標原點處。由于末端執行器為圓形，所以位姿的變化沒有影響，可以將末端執行器考慮為質點。

圖1 繩牽引并聯機構Fig.1 Cable-driving parallel mechanism

繩牽引并聯機構簡圖與坐標系如圖 2 所示，Mi(i=1，2，3，4) 為直線電動機，d為每組直線電動機運動方向，4 個出繩點為Ai(xi，yi) (i=1，2，3，4)，P為末端執行器，Fi(i=1，2，3，4) 為末端執行器所受各根繩上的拉力，出繩長度為Li(i=1，2，3，4)。實物框架用四邊形代替，4 個頂點為出繩點，并以框架中心點O為原點，建立直角坐標系Oxy。

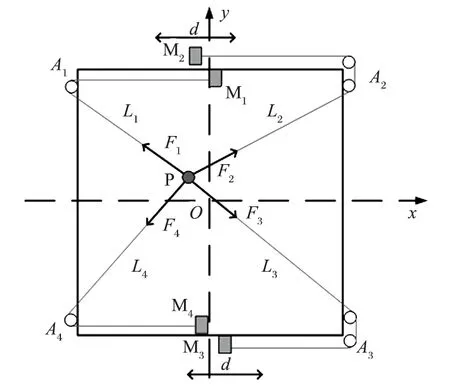
圖2 繩牽引并聯機構簡圖與坐標系Fig.2 Sketch and coordinate system of cable-driving parallel mechanism

1.2 運動學建模

設 4 根驅動繩的出繩長度為Li(i=1，2，3，4)，末端執行器的中心點坐標為P(x，y)，則根據運動學逆解公式[15-17]可得

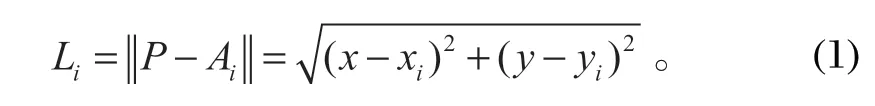
由圖 2 可知，4 組直線電動機沿x軸方向運動，y軸方向位置不變。出繩長度減去初始出繩長度，對應為末端執行器與直線電動機位置，直線電動機Mi(i=1，2，3，4) 沿x軸位置di(i=1，2，3，4) 如表 1 所列。其中LAiO(i=1，2，3，4) 為初始位置時的出繩長度即出繩點到坐標原點的距離。

表1 末端執行器與直線電動機位置關系Tab.1 Position relationship between end actuator and linear motor

由式 (1) 將繩長公式對時間求一階導即可得到繩索速度變化公式，可以具體表示為

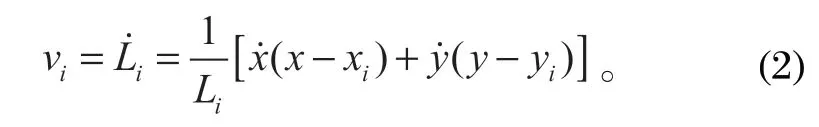
由式 (1) 將繩長公式對時間求二階導即可得繩長加速度變化公式，可以具體表示為

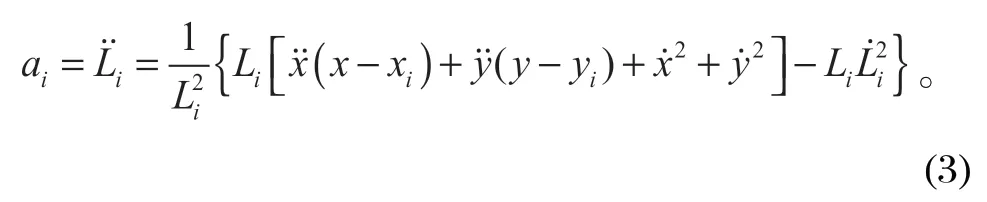
1.3 聯合仿真模型

繩牽引過程中繩索具有非線性，該因素會影響運動精度。為了反映繩索非線性因素對末端執行器運動精度的影響，用數學模型建模較為復雜，因此設計了聯合仿真模型進行仿真計算。該模型在 MATLAB/Simulink 環境下運行，建模步驟如下。

(1) 軌跡規劃 把時鐘信號和參考點信息代入軌跡規劃式，得到期望的末端執行器 P 運動中實時位置坐標。

(2) MATLAB 中逆運動學模型 將規劃的末端執行器P 軌跡代入式 (1)，就可以得到解算后電動機的位移Di(i=1，2，3，4)。

(3) Adams 中建立實體模型 把末端執行器 P 簡化成等質量小圓柱體，將直線電動機簡化成小滑塊，小滑塊要添加約束和驅動，驅動設置接口由 MATLAB中解算出的電動機位移Di(i=1，2，3，4) 提供。用Adams 中的繩輪模塊完成對繩索和滑輪的建立。繩輪模型要設置滑輪的位置、繩索的直徑、彈性模量等參數。仿真完成后，可以提取各電動機實際位移li(i=1，2，3，4) 即末端執行器運行軌跡。

聯合仿真模型的整體結構如圖 3 所示，參數設置如表 2 所列。

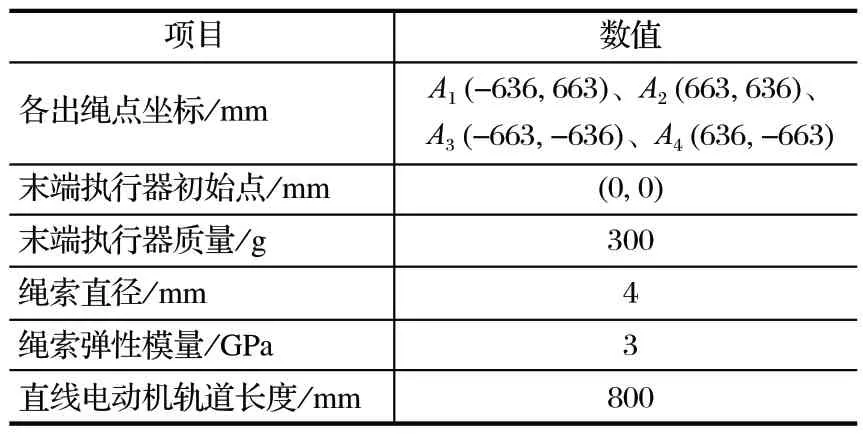
表2 繩牽引并聯機構參數Tab.2 Parameters of cable-driving parallel mechanism

圖3 仿真結構圖Fig.3 Simulation structure diagram

2 軌跡規劃

2.1 參考點選取

對多點的軌跡規劃可分為插值法與擬合法。由圖4 可以看出，插值法下末端執行器運動軌跡有序經過各個參考點；擬合法下運動軌跡不能準確的經過各個參考點，存在一定的誤差。

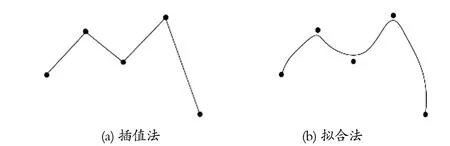
圖4 同一組參考點下的軌跡Fig.4 Trajectory at same set of reference point

當使用插值法，末端執行器經過參考點時，會出現以下 2 種情況：①若速度過快，突然改變速度方向產生較大的沖擊，會造成末端執行器振蕩影響運動精度；② 若速度過慢，失去對高動態末端執行器運動規劃的意義。因此，筆者采用擬合法開展軌跡規劃。

2.2 改進多項式軌跡擬合

試驗中，需要用不同曲率的拋物線軌跡來模擬不同情況下末端執行器的運動，以第 2 組拋物線為例，采用等x軸間距的方式把軌跡分成離散點，如圖 5、6所示。

圖5 不同曲率軌跡與參考點選取Fig.5 Various curvature trajectories and selection of reference point

從圖 6 可以看出，傳統插值法規劃的運動軌跡并不光滑，還可能會因為速度方向的變化而產生突變的力。為使擬合函數更加準確，筆者使用三次多項式進行擬合。

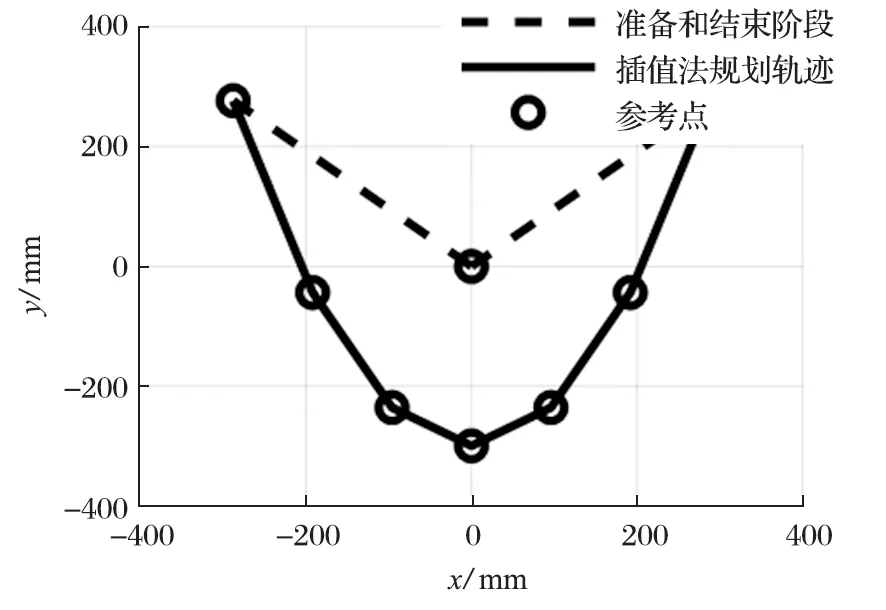
圖6 插值法末端執行器運行軌跡Fig.6 Motion trajectory obtained with interpolation method of end actuator

根據給定的n個數據點pi(xi，yi) (i=1，2，…，n)，求近似曲線，使得近似曲線在pi點處的偏差平方和最小。

設三次多項式為

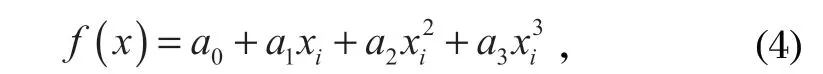
式中：ai(i=0，1，2，3) 為待定系數。

各點到這條曲線的偏差平方和

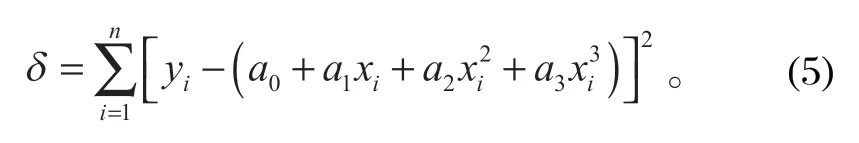
為了求得符合條件的a值，對每個系數求其偏導數為 0，即

對式 (6) 進行化簡處理可得

把等式 (7) 改寫為矩陣形式

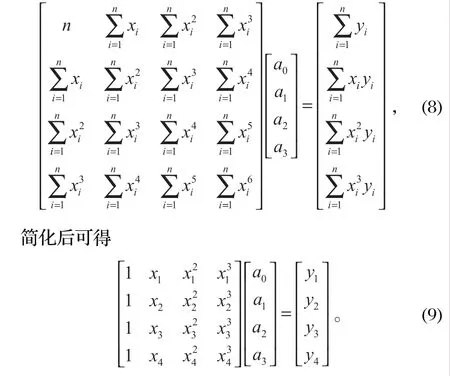
將數據點坐標代入式 (9)，求解可得ai(i=0，1，2，3) 的值。從而得到優化后的軌跡方程。由式 (9) 可知，要擬合 3 次多項式至少需要 4 個數據點，當數據點較多時可以去掉偏差較大的點。得到軌跡函數后，再進行梯形速度規劃，首先求出總路徑長度

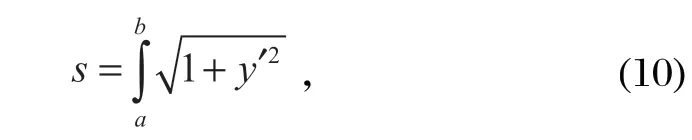
式中：a為軌跡起始點x軸坐標；b為軌跡結束點x軸坐標。

再將末端執行器整段運動路徑分為勻加速、勻速、勻減速階段，設勻加速階段和勻減速階段長度各占全軌跡長度的比例系數為k，則勻速階段占全軌跡長度的比例系數為 1-2k，這里假設k＝0.4，k值越大，勻變速階段路徑越長，則所需加速度越小。期望末端執行器的最大速度vmax為 2 m/s。

分別得到末端執行器勻加速階段s1(t)，勻速階段s2(t)，勻減速階段s3(t) 的表達式。

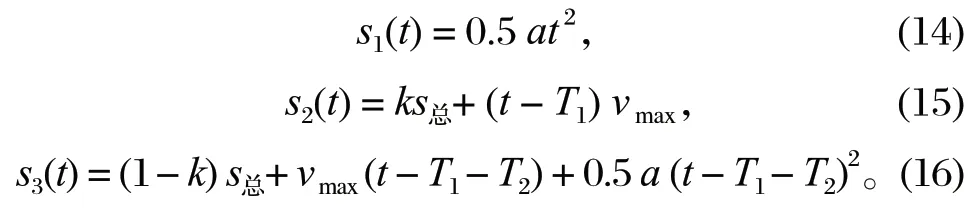
由此，可得到每個仿真步長已走過的路徑長度，再與軌跡起始點x軸坐標代入式 (10)，就得到每個仿真步長末端執行器所在的x軸坐標位置，再代入得到的軌跡函數式，就可得到末端執行器經規劃后的實時軌跡坐標。

3 仿真分析

設置仿真步長為 0.001。選取離散參考點如表 3所列，代入式 (4)～ (9) 可得到優化后的軌跡方程

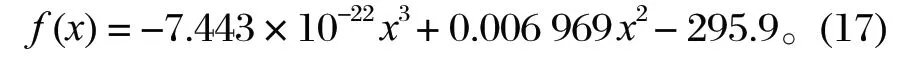
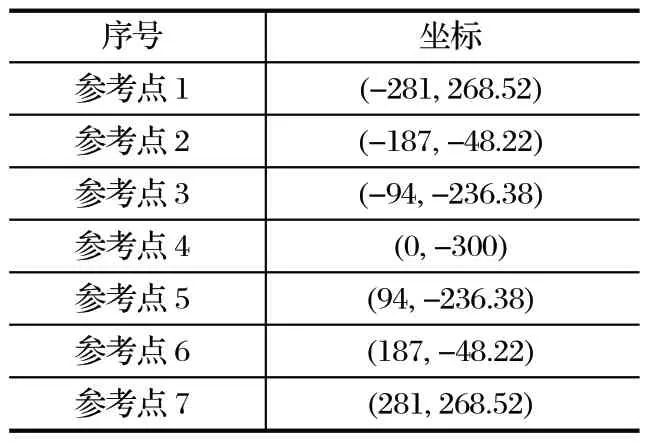
表3 參考點坐標Tab.3 Coordinates of reference point mm

優化后末端執行器運動軌跡如圖 7 所示。運行軌跡分為勻加速、勻速和勻減速階段，可以使末端執行器更長時間保持在峰值速度，提高運動效率。優化前后 2 種方法的運行軌跡如圖 8 所示。由圖 8 可以看出，改進多項式法優化后末端執行器的運行軌跡更加光滑，貼合期望物體運動情況。

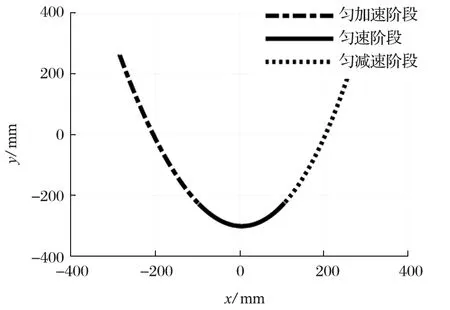
圖7 優化后末端執行器運行軌跡Fig.7 Motion trajectory of end actuator after optimization

圖8 優化前后 2 種方法下運動軌跡仿真Fig.8 Simulation on motion trajectory with two kinds of method before and after optimization

為清晰的對比優化前后電動機運動情況，以 1 號驅動電動機為例進行對比。1 號電動機位移仿真如圖9 所示。由圖 9 可以看出，優化后的電動機位移變化更加平穩順滑，波動更少，同時縮短了運行時間。1號電動機速度仿真如圖 10 所示。由圖 10 可以看出，優化后電動機的啟停次數為 4 次，而插值法啟停次數達到了 8 次，優化后電動機啟停次數減少了 50%。啟停次數減少，增加了保持在峰值速度的時間，同時避免了末端執行器運動中產生振蕩對運動精度造成影響。1 號電動機加速度仿真如圖 11 所示，由圖11 可以看出，使用優化方法后加速度減少了突變次數，使得末端執行器運動更加平穩，并且使用插值法時，最大加速度達到了 6.68×104mm/s2，而使用優化方法后，最大加速度為 4.76×104mm/s2，減小了約28.74%。

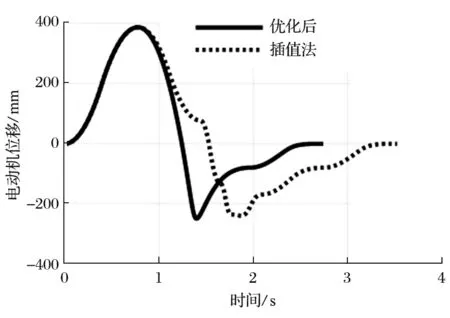
圖9 電動機位移仿真Fig.9 Simulation of motor displacement

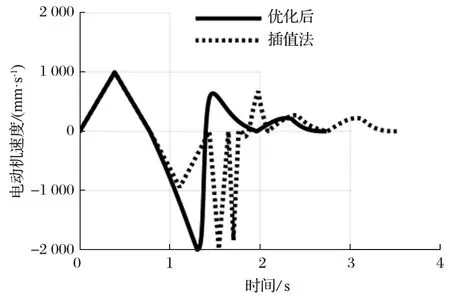
圖10 電動機速度仿真Fig.10 Simulation of motor velocity

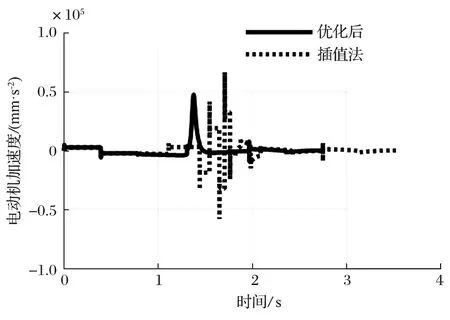
圖11 電動機加速度仿真Fig.11 Simulation of motor acceleration

從仿真時間可以看出，傳統插值法運行總時長需要 3.524 s，而經過優化后運行總時長只需要 2.740 s，縮短了 0.784 s，優化后的軌跡所用時間減少了22.25%，縮短了整體運行時間。

4 試驗驗證

選擇工控 PC 機作為控制器，在 TwinCAT 3 平臺上完成試驗樣機控制系統程序。將 2 種方法下的位置變化情況作為輸入信號，在試驗中通過 Twin CAT 3 中 Scope 模塊監測得到 4 組直線電動機實際運動情況。采用高速相機，對優化后的試驗軌跡進行了多次測量記錄，如圖 12 所示。

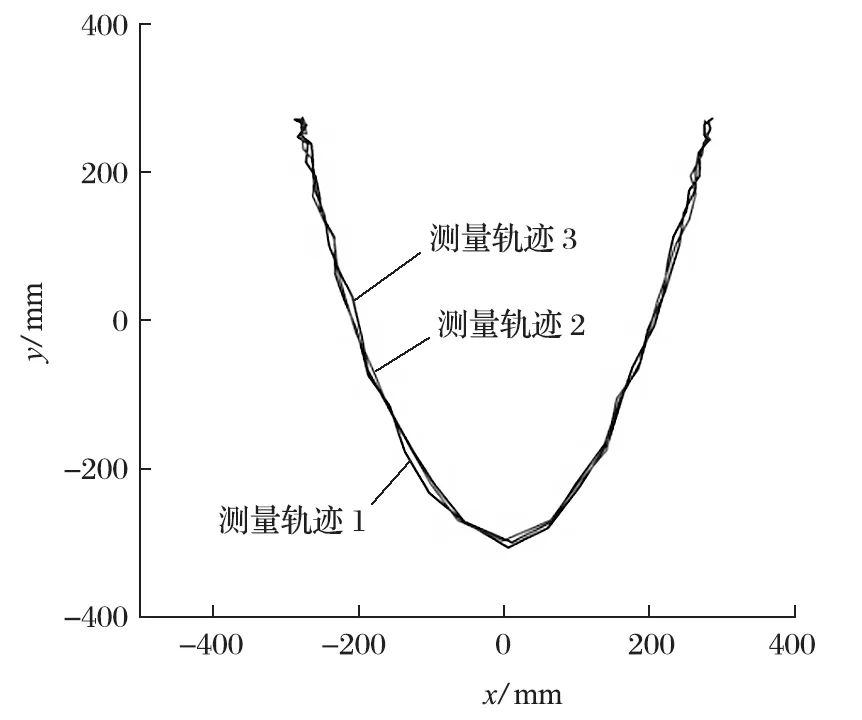
圖12 優化后多次測量軌跡Fig.12 Multiple measurement trajectories after optimization

仍以 1 號驅動電動機為例，對比優化前后直線電動機運動情況。優化前后 1 號電動機位移對比如圖13 所示。由圖 13 可以看出，優化后電動機位移更加平滑，與仿真結果基本相同。優化前后 1 號電動機速度對比如圖 14 所示。由圖 14 可以看出，使用插值法時，速度發生了突變，造成了較大的沖擊。造成這種現象的原因，可能是由于直線電動機頻繁啟停，導致響應不及時，并且在運動過程中造成了較大的噪聲。優化前后 1 號電動機加速度對比如圖 15 所示。由圖15 可以看出，采用優化方法后，直線電動機加速度變化次數減少，避免了末端執行器振動，與仿真趨勢基本一致。

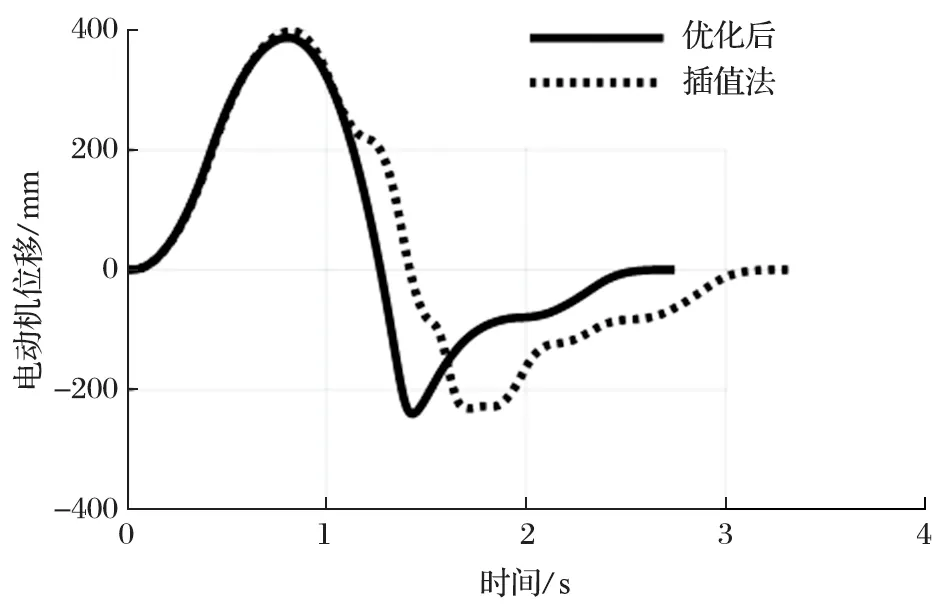
圖13 電動機位移對比Fig.13 Comparison of motor displacement

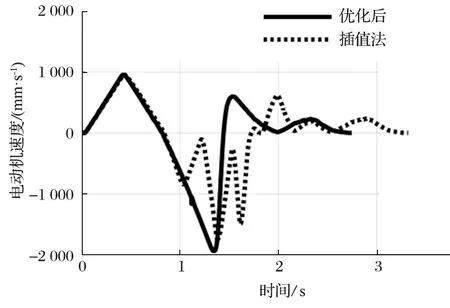
圖14 電動機速度對比Fig.14 Comparison of motor velocity

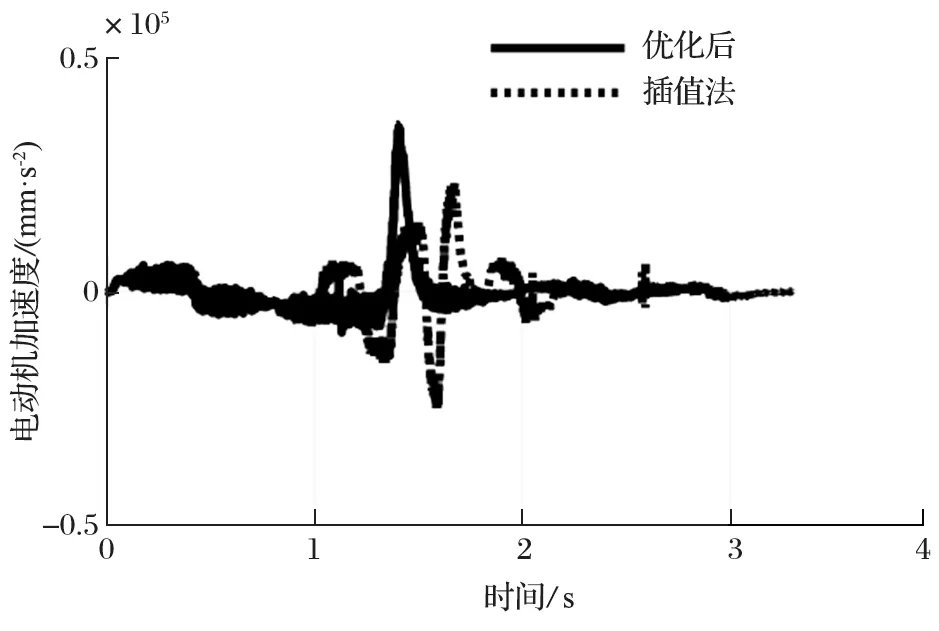
圖15 電動機加速度對比Fig.15 Comparison of motor acceleration

對比仿真與試驗結果可以看出，仿真結果與試驗結果變化趨勢相同，驗證了仿真模型的準確性。

5 結論

(1) 通過仿真分析，改進多項式法可對末端執行器軌跡與直線電動機運動性能進行優化。優化后的末端執行器軌跡更加平滑，縮短了運行時長；直線電動機位移波動明顯減小，并且啟停次數減少，避免了沖擊與振動的影響。

(2) 搭建了試驗樣機，對傳統插值法和改進多項式法進行了試驗對比。結果表明，使用改進多項式法優化后，直線電動機位移、速度和加速度曲線更加平滑。

(3) 通過仿真與試驗結果對比可以看出，各直線電動機的位移、速度以及加速度情況基本相同。驗證了聯合仿真模型的準確性。