矢量數據多尺度表達圖譜認知理論與計算

宗 琴，劉艷霞，陳明建，秦萬英

（1. 重慶建筑工程職業學院，重慶 400000；2. 武漢市測繪研究院，湖北 武漢 430072）

在地理空間數據呈幾何級數增長中，出現了較為突出的兩個問題。一是對于地理空間數據的存儲管理而言，各行業部門在開展國家空間數據基礎設施建設工作時，由于對地理空間數據的應用要求不同，導致在數據結構、數學基礎、空間尺度、空間參考、語義以及幾何位置等方面存在不一致；二是盡管國家投入了一定經費加強建設數據共享機制；但仍出現了地理空間數據生產隨機性大、數據更新和共享管理機制不健全等問題。因此，如何對海量、多源、異構的地理空間數據進行管理、分析和更新成為當下相關科研機構、管理部門著重研究的課題[1-14]。

1 矢量信息圖譜

1）矢量信息的“圖”特征，是指描述地理空間實體的輪廓線條表征出的形態、大小、面積、輪廓、結構等，相比遙感信息的“圖”特征，矢量信息的“圖”特征更適應多尺度表達，因為其不會隨著尺度變化而失真。目前自動綜合技術對多尺度空間數據表達的限制使得矢量信息無法實現連續化表示，但“圖特征”可以實現以其抽象、簡潔、形象的符號離散化地表示地理信息。

2）矢量信息的“譜”特征，是指矢量數據表征出的類別、方向、關系、規律、變化等，相比遙感信息的“譜”特征，矢量信息雖沒有光譜維信息，但其隨尺度變化表現出的譜系更易量化。“圖特征”實現了離散化表示地理信息，“譜特征”則完成了連續化表示，以運動、系列的譜系定量表示地理信息。

綜上所述，矢量數據和遙感影像作為空間數據的組成部分，也具備了“圖”和“譜”的綜合信息，兼有“圖形”與“譜相”的雙重特性。矢量數據圖譜合一的特性是多尺度表達的結果，反映了地理空間實體的地理屬性，譜寫了地理空間實體在空間分布、時間推移、尺度變化上的表現，是進行地理信息認知的起點和立足點[2，15-16]。

2 矢量信息圖譜特性

矢量信息圖譜的目標對象是地理空間實體，如同知識圖譜本質上揭示實體之間關系一樣，矢量信息圖譜本質上具有目標的動態性、目標的相似性、關系的細粒度分析等3 個方面的特性，基于這3 個方面的特性，矢量信息圖譜揭示著地理空間實體的關系，得以實現從理論上認知矢量數據的多尺度表達。

1）目標的動態性：指矢量信息圖譜自動識別出同類事物，即某地理空間實體形態發生變化后，自動識別出它變化后的形態信息。

2）目標的相似性：指目標對象在不同尺度上的綜合相似性。地理空間實體表達為計算機世界的空間數據后，連續尺度表達下的“圖”特征和“譜”特征存在局部差異，但綜合來看是相似的，這也驗證了朱阿興[17]等提出的地理相似性是地理學的第三定律。

3）關系的細粒度分析：地理空間實體因為實體類型不同表現出多樣化，實體之間的關系也可能存在細粒度的不同，即要素級、目標級和幾何特征級等不同層次的粒度，要素級的粒度最粗，幾何特征級的粒度最精細，矢量信息圖譜可以呈現出精細的實體關系。

3 矢量數據多尺度表達圖譜認知理論與計算

矢量數據多尺度表達由地理信息自動綜合技術實現，但目前自動化綜合技術還處于理論研究階段，真正的全智能化全自動化綜合技術實時提取任意尺度表達的數據尚處于發展研究階段。如若完成矢量數據多尺度表達圖譜認知理論和計算方法論，多尺度空間數據庫相關問題必將邁上新的臺階。下文將從“由圖抽譜”、“圖舊譜新”和“相譜相成”3 個階段對認知理論進行論述。

3.1 由圖抽譜

矢量數據的圖形特征因實體對象的維度不同而有不同的描述方法。對于點實體而言，描述點實體的空間數據僅僅是單一的坐標，無法構成圖形，常常將其升維為面群進行描述；對于線實體而言，描述線實體的空間數據是一系列坐標串，往往把首尾起止點連接形成封閉的面實體進行描述。基于這樣的升維思想，矢量數據的圖形特征更多的是面實體的幾何特征。常見的特征包括面積、周長、內角、Feret直徑、面積周長比率等。大部分學者專研于這些特征的描述方法，較有成效的包括形狀中心點位置法、凸包法、包圍盒法、重心射線法、重疊面積法、離散幾何矩法、方位編碼法和相對參數法等。這些描述方法更多地服務于實體之間的匹配，以實現數據更新、變化檢測、數據融合等方面的應用，而挖掘圖形特征中描述矢量數據發展規律的譜特征則是由圖抽譜的智能化目的。

3.1.1 面實體圖特征

面狀實體的輪廓可以看作一系列輪廓點沿著指定的方向（順時針或者逆時針）首尾相連形成的。已知某面狀實體A的形狀輪廓表示構成輪廓的輪廓點，n表示輪廓點的數量，每個輪廓點P'(i)的坐標為如圖1所示。

圖1 面狀矢量數據輪廓點提取

有了輪廓點的概念，相鄰2個輪廓點則構成輪廓線段，輪廓線段再由有序的點相連成面實體形狀輪廓。已知n個輪廓點P'(i)(i∈[1,n]) 組成的面實體形狀輪廓S'，以每對相鄰的2個輪廓點P'(i)與P'(i+1) 構成一個輪廓段l'(i)，則此時的形狀輪廓可表示為S'={l'(i)|i∈[1 ,n] }，l'(i)表示第i個輪廓段，n表示輪廓段的數量。

構成一個面實體形狀輪廓的輪廓點數量往往比較多，因此利用等間隔采樣的方法采樣輪廓點從而簡化計算過程，得到采樣后的輪廓點集合S={P(i)|i∈[1 ,m] }，P(i)為重采樣后的輪廓點；m為重采樣后的輪廓點數量。圖2 表示重采樣后的面狀實體，可見適當的采樣頻率能夠在減少輪廓點數量的同時保留形狀細節，所以形狀輪廓可以表示為S={l(i)|i∈[1 ,m] }，l(i)為由重采樣后的輪廓點構成的輪廓段（圖2）。

圖2 重采樣后的面狀矢量數據

按照參考文獻[18]針對柵格數據模型的提取策略，提取面實體的圖特征，提出如表1 所示的圖特征要素。本文將輪廓距離定義為從形狀輪廓段的起點沿著輪廓，到另一端點所經過的輪廓長度為輪廓段的輪廓距離。輪廓段lk(i)兩端點P(i)和p(i+ak)的輪廓距離codk(i)：從起點P(i)到終點p(i+ak)沿著輪廓經過的所有輪廓點，每對相鄰接輪廓點的歐氏距離之為：

表1 面實體圖特征要素

式中，p(j)∈C(i)；C(i)為輪廓段lk(i)從起點P(i)到終點p(i+ak)構成輪廓路徑的輪廓點集合。

3.1.2 面實體譜特征抽取

由面實體的圖特征抽取面實體的譜特征，組成參數包括3.1.1 中的歐氏距離、輪廓距離、輪廓距離之和與形狀內距離。抽取的譜特征包括歸一化形狀內距離、形狀內距離變化率、歸一化形狀內距離與輪廓距離的比值、歸一化歐氏距離與形狀內距離的比值、歸一化歐氏式距離與輪廓距離的比值（如表2）。

表2 面狀實體譜特征

抽取如表2所示的面實體譜特征，即：

式中，k表示當前尺度層序數；K為尺度的總層數；這里選擇6個尺度及K=6

3.1.3 面實體譜特征尺度化

采樣后的面實體有m個輪廓點，輪廓段lk(i)表示從起點p(i) 按逆時針方向以間隔ak個輪廓點的p(i+ak)為終點構成的輪廓段，其中：

式中，k為當前尺度層序數，以6 個尺度為例，那么采樣后的輪廓點p(i)為起點構成的多尺度輪廓段分別為以輪廓點為終點構成的輪廓段。從公式（12）中可以看出，當K=6 時，表示最小尺度輪廓段，此時lk(i)最短，包含的形狀輪廓最小，體現了實體的局部特征；當K=1 時，表示最大尺度輪廓段，此時lk(i)最長，即第一層尺度時表示輪廓段最長，包含了面實體的半全局特征。

這樣，對于采樣后的實體，每個輪廓點在每個尺度上都有5類特征參數，即每個輪廓點p(i)都有5×K個特征參數，分別代表了以p(i)輪廓點為起點的面實體的局部細節與全局整體特征。

3.2 圖舊譜新

矢量數據多尺度表達，常規的表達思維是根據不同的應用存儲靜態的不同尺度的數據版本，或者存儲精細的數據版本再根據應用進行動態綜合，尚未實現真正意義上的全自動表達。實際上構成矢量數據的主要空間實體面實體，其形態的變化規律如果組建圖譜，那么多尺度表達便可開辟新的路徑。

面實體在當前尺度下的圖特征本身是靜態化的屬性，而當前尺度下的譜特征可以動態化，從而預測下一個尺度的圖特征（這一構建思想在早期的研究中已有說明）。設當前尺度為N，面實體A、B、C分別為尺度N，N-1，N+1 下的面實體，其輪廓點為pi和qj與rk，兩實體之間的距離函數定義為d(pi,qj)和d(pi,rk)，即：

其中：

為了推算尺度N+1 下的面實體C 的輪廓點特征，以面實體A 輪廓點的特征序列為行向量，以面實體B輪廓點的特征序列為列向量，利用前面定義的距離函數構成距離矩陣。

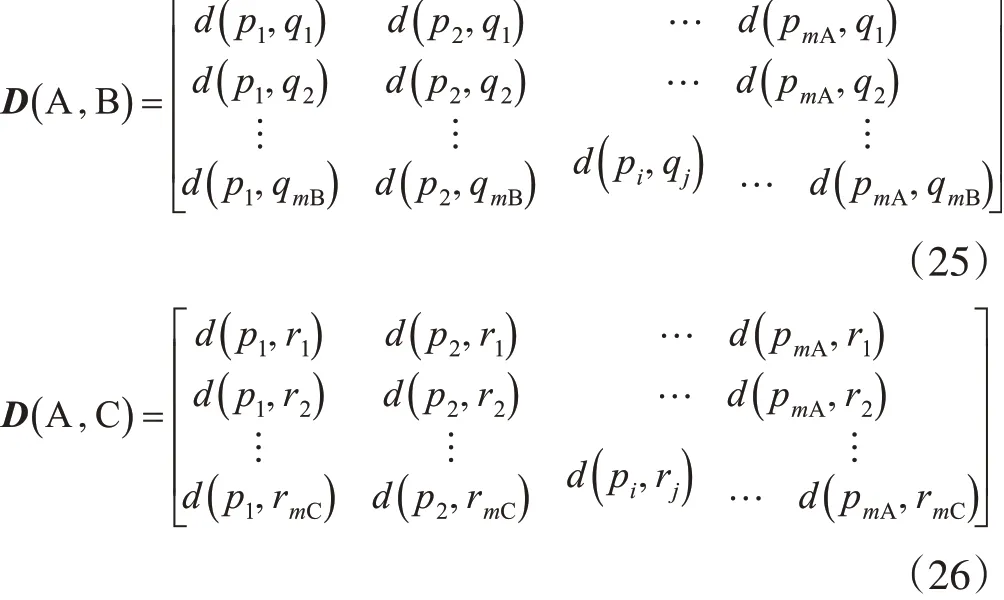
通過計算尺度N和尺度N-1 下的距離矩陣，以及尺度N-1和尺度N-2 下的距離矩陣，發現距離矩陣變化規律，從而推算尺度N和尺度N+1 下的距離矩陣，由此反演尺度N+1 下的C 實體的輪廓點及其圖特征。

4 結 論

在大數據時代，地理信息的飛速增長使得現勢數據呈現堆積的狀態，隨之出現的數據融合、聯動更新、變化檢測方面的問題限制了矢量數據的及時應用。本文對矢量數據多尺度表達圖譜理論進行了論述，從根源上剖析地理空間實體認知規律，為大數據背景下的地理信息研究提供相應的參考。