融合kmeans 聚類與Hausdorff 距離的點云精簡算法改進

彭海駒，嚴科文*，林 松，賴浩源，張澤鑫

（1. 惠州市自然資源規劃勘測院，廣東 惠州 516000）

隨著三維激光掃描技術的不斷發展，點云精簡成為高效處理海量的點云數據重要技術手段。常用的點云精簡方法有體素下采樣法[1]、曲率采樣法[2]、基于聚類的精簡方法、隨機采樣法。相關研究人員對幾種方法分別進行探討，歸納出其面臨的問題有容易丟失特征點數據、精度較差、曲率估算精度較差問題等[3-4]。針對上述問題，本文對融合kmeans 聚類與Hausdorff距離的點云精簡算法進行改進，基于其對特征區域和非特征區域采用不同特征點提取策略的原理，在非特征點區域仍然采用kmeans 聚類算法提取特征點，但采用手肘法確定聚類數，保證聚類精度。在特征區域采用維數特征Hausdorff 距離代替主曲率Hausdorff 距離提取特征點，避免了曲率的估算和在曲率值過小時設定Hausdorff 距離閾值，最后融合kmeans 聚類簇心與采用維數特征Hausdorff 距離提取的特征點實現數據精簡。

1 融合kmeans與Hausdorff距離的點云精簡算法

1.1 kmeans聚類算法

kmeans 聚類算法中的k代表聚類個數，means 代表取每一個聚類中數值的平均值作為該簇的中心，即每一個簇都用這個類的中心描述[5]。這種聚類算法容易實現，其具體實現流程如下：

1）確定簇的個數k。

2）計算各個采樣點到簇中心的距離，一般是歐氏距離。

3）根據新劃分的簇，更新“簇中心”。

4）重復步驟（2）和步驟（3），直到“簇中心”不再移動。

1.2 Hausdorff距離

Hausdorff距離是一種描述兩組點集之間相似程度的量度[6-7]，若存在兩組數據點A={a1,a2,…,an} ，B={b1,b2,…,bn} ，則這兩組數據的單向Hausdorff 距離為：

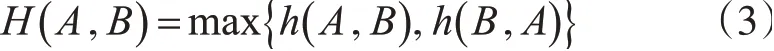
1.3 算法描述

融合kmeans 與Hausdorff 距離的點云精簡算法首先建立空間索引，然后基于局部點云數據擬合局部曲面，再通過擬合曲面估計采樣點的2 個主曲率值。對于某一采樣點pi和其鄰域內某點qj的主曲率分別為k1、k2和k1'、k2'，則采樣點與其鄰域內點曲率的Hausdorff距離計算公式如下：

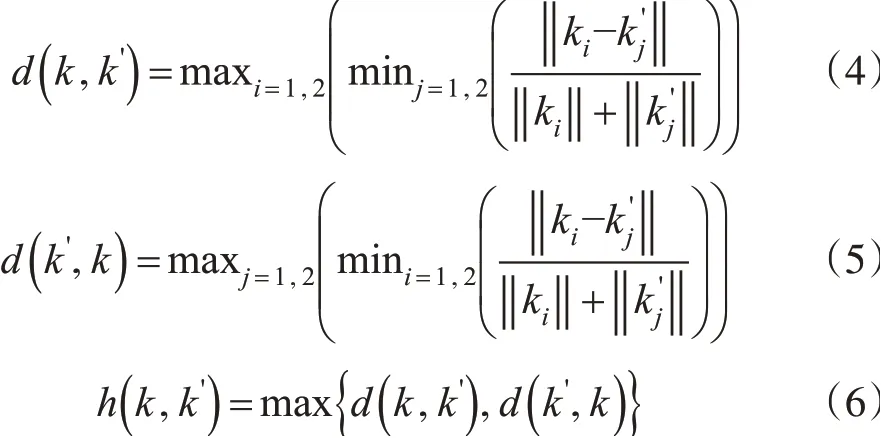
因此，采樣點pi的Hausdorff距離可以表示為：

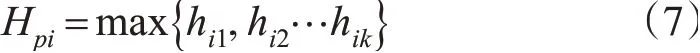
該方法通過設定Hausdorff距離閾值實現特征點云的提取，然后對于非特征區域采用kmean 算法聚類，將每個聚類中心作為非特征區域的特征點與通過Hausdorff距離閾值提取的特征點融合完成精簡。

2 改進的融合kmeans與Hausdorff距離的點云精簡算法

2.1 手肘法

手肘法是一種確定數據聚類最優聚類數的方法[8]，李健[4]等采用平均密度計算kmeans聚類數，并沒有考慮聚類精度，對于聚類結果通常采用SSE作為精度檢驗指標，其計算公式如式（8）所示。而手肘法的核心思想就是使得SSE 最小。對于kmeans 來說，k值取得越大，則樣本的劃分更加精細，每個簇的聚合程度更高，則SSE越小。并且，當k的取值小于真實聚類數時，SSE 會隨著k值的增大迅速下降；當k達到真實聚類數時，SSE 的下降幅度會驟減。隨后繼續增大k值，SEE 會慢慢趨于平緩。SSE 和k值的關系圖與一個手肘相似，而這個肘部對應的k值就是真實聚類數。

式中，Ci為第i個簇；p為Ci中的采樣點；mi為Ci的質心。

以斯坦福大學兔子點云為例，其原始點云數據如圖1所示，共8 171個點。采用手肘法，以100個聚類數作為步距，計算聚類個數在100～8 000 的SSE 值，結果如圖2 所示。圖中隨著k值的不斷增大，SSE 不斷減小，且整個圖形符合手肘法的趨勢。分析圖2 可知，當k小于1 000時，SSE的下降幅度較大；當k大于1 000時，SSE開始緩慢下降，故對于該兔子點云數據的聚類個數可取值為1 000，圖3 為k取1 000 時兔子點云聚類效果圖。

圖1 原始兔子點云

圖2 聚類個數與SSE間關系

圖3 k=1 000 聚類結果

2.2 維數特征

主成分分析法（principal component analysis，PCA）是一種數學降維方法[9]，能夠將原來變量重新組合成一組新的互不相關的幾個綜合變量，從綜合變量中選取部分綜合變量能較完整的反映原來變量的統計信息。對于采樣點P，其鄰域點集為Pi=[xi yi zi]，則可以通過式（8）得到P點的協方差矩陣M。

式中，k為P點鄰域點個數；Pˉ為P點鄰域點集的質心點坐標；M是一個對稱半正定矩陣，故其矩陣的3 個特征值都為非負值，對于點云數據，則這3 個特征值所對應的特征向量為兩兩正交的向量。

對采樣點P鄰域內點集進行主成分分析可以得到3 個特征值λ1、λ2、λ3，其中λ1≥λ2≥λ3，這3 個特征值之間有以下關系：

1）λ1≥λ2≥λ3時，局部區域表現為線型，如圖4a所示。

2）λ1≈λ2≥λ3時，局部區域表現為面型，如圖4b所示。

3）λ1≈λ2≈λ3時，局部區域表現為球形，如圖4c所示。

圖4 特征分析示意圖

依據3個特征值按式（9）定義了維數特征[10]，其中，a1D+a2D+a3D=1。特征維數描述了局部區域點云數據的空間分布特征。

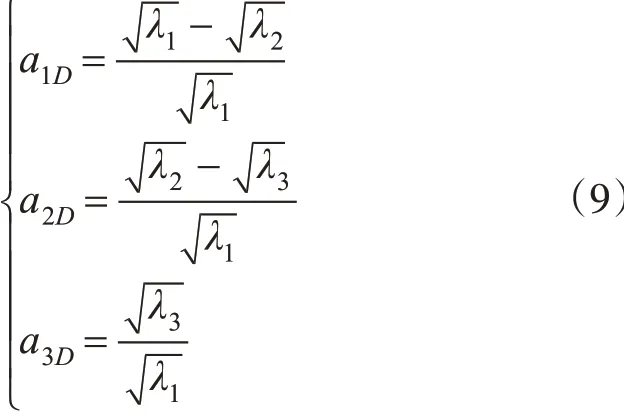
2.3 改進后算法

在李健[4]等提出的融合kmeans 與Hausdorff 距離點云精簡算法的基礎上，先采用維數特征的Hausdorff 距離提取特征點，再對剩余非特征點利用手肘法確定最優聚類數，以每個聚類中心點作為非特征區域內的特征點，保證數據均勻，不造成空洞。改進后的算法首先避免了在平面區域曲率值過小而需要設定閾值的問題，同時在確定聚類數中也保證了聚類精度。

對于某一采樣點pi和其鄰域內某點qj的特征維數分別為a1D、a2D、a3D和則采樣點與其鄰域內點維數特征的Hausdorff距離計算公式如下：

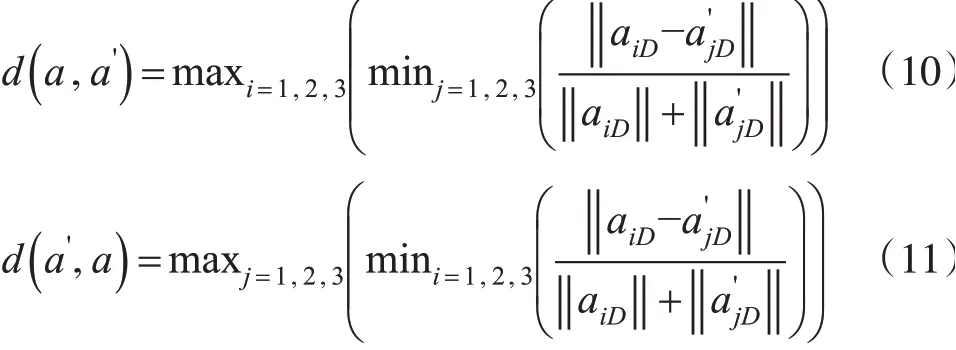
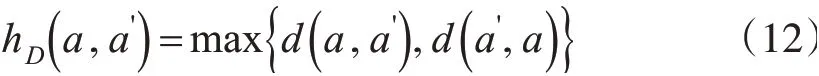
因此，采樣點pi的維數特征Hausdorff 距離可以表示為：

3 實例驗證與分析

采用Rigel VZ-1000掃描儀對某古亭建筑進行高密度多站掃描，依據標靶球粗配準后，再采用最近點迭代算法（iterative closest point，ICP）精配準，然后利用SOR算法去除少量體外孤點，利用拉普拉斯濾波算法平滑表面毛刺點，配準去噪后點云數據如圖5a所示。

本文通過將改進的精簡算法與李健提出的精簡算法、基于曲率的精簡算法、隨機采樣精簡算法和體素下采樣精簡算法的實驗結果進行比較，來評價改進后的方法，5 種精簡方法實驗結果如圖5b、c、d、e、f所示。

圖5 不同精簡方法實驗結果

原始點云個數為726 417個，采用5種精簡方法將古亭點云都精簡至20%左右。基于曲率采用和隨機采樣2 種方法在檐頂剔除了大量數據點，特別是基于曲率的精簡方法造成了數據整體分布不均勻，本文方法、文獻[5]方法和體素下采樣方法都能夠獲得較為均勻的數據。圖6為本文方法和文獻[5]方法提取特征點和非特征區域內特征點的結果圖，其中對于文獻[5]中基于曲率Hausdorff距離提取68 415個特征點，如圖6a所示；采用本文方法中基于維數特征Hausdorff距離提取70 791個特征點，如圖6d所示；依據手肘法確定最優聚類個數約為70 000個，為保證相同精簡率，對于文獻[5]中剩余非特征區域依據剩余非特征點密度提取聚類中心點73 057個點，如圖6b所示；本文方法對于剩余非特征區提取聚類中心7 000 個點，如圖6e 所示；文獻[5]方法和本文方法融合特征點和非特征區域特征點結果如圖6c、f 所示。可以看出雖然提取的特征個數相同，但是本文方法的特征點相較于文獻[5]方法在檐頂的特征點更多。

圖6 2種Hausdorff距離提取特征點及非特征區域特征點圖

為了定量分析5種精簡算法的精簡精度，對精簡后的點云數據建立三角網，通過統計三角形個數和三角形總面積來評定精簡精度[11-12]。統計結果如表1 所示。以原始點云三角形總面積近似為真值，采用其他5 種精簡方法精簡后的點云構建的三角網總面積都小于真值，符合精簡后的數據精度有損失的規律，其中采用本文方法精簡的結果最接近真值，其表面精度損失較少，即精簡精度相對于其他4種方法精簡精度較高。

表1 不同精簡方法的結果比較

4 結 語

本文改進了融合kmeans 聚類和Hausdorff 距離的點云精簡方法，通過對聚類數的確定和Hausdorff距離計算參數加以改進，提出了先通過計算特征維數的Hausdorff距離提取特征點，然后采用手肘法確定剩余非特征點的最優聚類數，將特征點和聚類中心數據融合作為點云精簡結果的技術路線；最后通過實際掃描的古亭建筑的點云數據，分別采用本文方法，文獻[5]方法、基于曲率采樣、隨機采樣和體素下采樣5 種方法進行精簡實驗，結果表明改進后的方法在相同的精簡率下精度更高。