地下水滲流作用下地下洞室塊體穩定性分析

朱杰清

(中國電建集團福建省電力勘測設計院有限公司，福建 福州 350003)

0 引言

地下巖體中結構面的存在會直接降低圍巖的強度[1-3]，巖體被不同尺度、產狀的結構面切割形成的塊體具有一定的隨機性，從塊體開挖揭露到通過計算判斷塊體的穩定性通常需要一定時間，在這段時間內若不及時采取措施，塊體有可能失穩滑落，這給地下洞室工程的開挖過程帶來不可預知的風險[4]。

地下洞室開挖后，圍巖內部的應力場和滲流場發生耦合作用，地下水通過巖體內部的結構面向洞室方向滲流，經力學、物理及化學作用，易發生圍巖失穩等問題[5-8]。因此，在研究地下洞室圍巖穩定性的問題時，考慮地下水滲流作用十分必要。目前，許多學者針對這個問題進行了大量研究，并取得了一些成果。王明等[6]基于有限元數值方法得到裂隙巖體的滲流對地下洞室圍巖穩定產生不利的影響；谷拴成等[7]應用等效分析方法研究滲流作用下錨桿支護巷道的穩定性，得到滲流作用時需要錨桿提供更大的支護力；李鵬飛等[8]討論了滲流作用下海底隧道掌子面圍巖的穩定性問題，發現滲流作用使得開挖面上部地層變形量明顯大于下部。

本文依托某工程實例，利用極限平衡法和離散單元法進行模擬計算，分析洞室開挖過程中有無滲流作用下楔形體的穩定性，并分析兩種方法的優缺點。

1 極限平衡法和離散元法基本原理

1.1 極限平衡法

極限平衡法是根據靜力平衡原理分析不穩定塊體的受力狀態，以滑動面上阻滑力和下滑力間的比值(穩定系數)來評價塊體穩定性。

計算方法如下所示：

(1)

式(1)中，F為穩定系數。

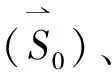
①脫離巖體

(2)

②沿單一結構面滑動

(3)

(4)

式(4)中，αi為結構面i的傾角，βi為結構面i的傾向。

③沿兩條結構面滑動

(5)

不穩定塊體的有效滑動方向按照表1的判據進行確定，滿足其中的哪個判據就是不穩定塊體的滑動方向，如果都不滿足表1中的判據，則塊體處于穩定狀態。

表1 不穩定塊體滑動方向判據及各結構面上的法向力

1.2 離散元法

離散單元法(簡稱DEM)是由Cundall在1971年首次提出，專門用來解決非連續介質問題的數值模擬方法。該方法把節理巖體看成由離散的巖塊和巖塊間的節理面組成，塊體的幾何形狀取決于巖體結構中不連續面的空間位置及其產狀，通過牛頓第二定律來表征塊體的運動過程，并允許巖體的內部可以發生塊體的大位移、旋轉、滑動甚至塊體的分離等運動，借此可以達到比較真實地模擬節理巖體中的非線性大變形特征。

3DEC離散元數值分析軟件主要以離散單元法為基本理論來描述離散介質的力學行為，它將介質離散成為連續性特征(巖塊)和非連續特征(結構面)兩個基本元素的統一集合體，并通過成熟的力學定律來描述這些基本元素的受力變形過程。

2 實例計算

2.1 工程概況

某直墻圓拱型地下洞室開挖時邊墻出現不穩定楔形塊體滑落事件，該楔形體(圖1)是由兩個節理面、一個斷層面共同切割，加上洞室開挖臨空面形成一個不穩定四面體，結構面產狀依次為：80°∠35°，250°∠60°，130°∠81°，楔形塊體體積約8.15m3。斷層處巖體較破碎，結構面由遇水軟化的黏土礦物充填。根據現場反饋，開挖此段時巖體穩定，未有明顯滲水現象，次日打完錨桿孔后，出現明顯滲水現象，且水量較大，當開挖面推進約59m時，楔形塊體發生滑塌。分析認為，地下水是導致楔形塊體發生滑塌的主要原因之一。

圖1 現場圖片

2.2 極限平衡法計算

結構面的參數根據現場情況和《工程巖體分級標準》(GBT50218-2014)確定，計算時取節理面粘聚力為30kPa，內摩擦角為25°，斷層面粘聚力為20kPa，內摩擦角為20°。計算過程如下：

①確定結構面的法向量

②主動力計算

A=W=(γV)·g=(0 0 -211.9)

③確定滑動方向

根據上文滑動方向判據可知楔形塊體沿節理面2即滿足：

因此，此楔形塊體滑動方向為：

④計算阻滑力

N1=N3=0

τ=c+σtanφ=31.7kN/m2

J2=τacosθ=330.4kN

J1=J3=0

⑤計算穩定系數

根據現場施工反饋，巷道開挖至此段時圍巖穩定，巷道順利通過，之后發生明顯滲水現象，且水量較大，當巷道往前推進59m時，此處發生圍巖小面積滑落事件。由此可見，地下水的作用不可忽視。

假定斷層面的水壓為20kPa時，此時：

A=W+U=(-103.9568 87.2353 -233.3894)

楔形塊體滑動方向為：

楔形體的穩定系數為:

當斷層面的水壓為30kPa時，此時：

A=W+U=(-155.9352 130.8529 -244.134)

楔形塊體滑動方向為：

楔形體的穩定系數為:

此時，不穩定楔形體的安全系數小于1 ，塊體將發生滑落。

如表2所示，隨著地下水壓力的增加，不穩定楔形體的穩定系數逐漸降低，圍巖穩定性下降。

表2 不同水壓力下楔形體的穩定系數

利用極限平衡法計算時假定結構面為平面，而實際上巖體中的節理都是隨機分布的，同一組節理由于多種因素的影響，變動性較大，結構面也并不全部是平面，稍有不準確，就會使計算結果有較大的偏差；計算時假定洞室開挖的軸線方向始終保持不變，對于稍微復雜的大型工程來講，顯然是不能完全滿足工程要求的。

2.3 離散元法計算

利用3DEC離散元軟件，針對該滑落事件進行穩定性的模擬計算，建立模型尺寸為50m×30m×50m。另外，考慮斷層破碎帶，斷層出露厚度為4m(沿巷道軸向)，在巷道右邊墻斷層破碎帶處按產狀130°∠81°、80°∠35°、250°∠60°切出一個四面楔形體，如圖2所示。

圖2 洞室塊體算例模型

模型假定巖塊不產生滲流，地下水僅在裂隙中流動，初始地下水壓力場按重力梯度設置。模型的左側、右側、前側和后側邊界設為固定孔隙水壓力，并且服從重力梯度。模型頂面和底面為定水頭邊界，其中頂面設定水壓力為0.185MPa，底面設定水壓力為0.685MPa。

根據勘察資料，該段交通巷道圍巖質量等級Q值范圍在1～10之間，斷層破碎帶Q值為0.04，故本次模擬圍巖取1≤Q<4，斷層處取0.01≤Q<0.1。巖體物理力學參數見表3。

表3 巖體物理力學參數

考慮滲流情況時，設定節理初始隙寬b0=1×10-4m，最大隙寬bmax=1×10-3m，殘余隙寬br=1×10-5m。

2.3.1 應力場分布特征

如圖3、圖4所示，滲流情況下洞室周邊最大主應力和最小主應力比無滲流情況下小，且滲流情況下洞室圍巖局部產生0.185MPa的拉應力，圍巖產生拉破壞。其主要原因是地下水滲流時，水的滲透壓力和拖拽力加劇了裂隙的剪切和拉裂破壞，應力得到釋放而導致。

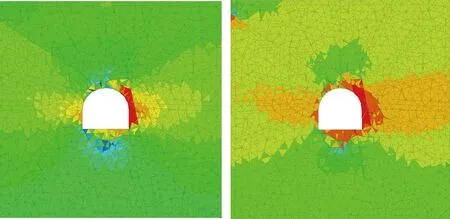
(a)無滲流情況(b)滲流情況

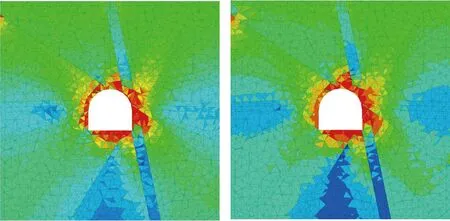
(a)無滲流情況(b)滲流情況

2.3.2 位移場分布特征

如圖5所示，無滲流條件下楔形體區域的最大位移為37.6mm，滲流條件下的最大位移最大值為130.4mm，楔形體整體出現較大的變形。

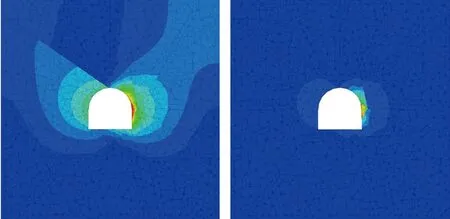
(a)無滲流情況(b)滲流情況

2.3.3 塑性區分布特征

如圖6所示，由于存在斷層，巷道周邊的塑性區范圍都較大，滲流條件下巷道周邊塑性區的范圍和厚度比無滲流情況下更大，塑性區體積增大約1000m3。其主要原因是由于巖體中的地下水使得圍巖強度降低，進而導致圍巖破壞的區域越大。

離散元法的優勢在于其可以較好地實現塊體間的分離、旋轉及塊體垮落等大位移運動的過程，又能計算巖塊內部的變形與應力分布。同時，能夠考慮初始地應力、圍巖變形和非滑面抗剪性能對塊體穩定性的影響，計算更符合實際情況。對大型地下工程，洞室開挖后，圍巖會產生裂隙和發生大規模垮落，在這種條件下利用3DEC軟件計算可使地下工程的模擬解更為合理。

(a)無滲流情況(b)滲流情況

3 結束語

本文利用極限平衡法和離散元法分別計算有無地下水滲流作用時地下洞室不穩定楔形體的穩定性，結果表明，地下水的存在會降低不穩定楔形體的穩定系數。通過對比分析，考慮地下水滲流作用下，楔形體及周邊圍巖的主應力比不考慮滲流情況下小，楔形體及周邊圍巖的位移量和塑性區面積比不考慮滲流情況下大，圍巖的穩定性比無滲流情況下更差。