學生的『深度理解』是怎樣煉成的
——特級教師夏永立《除數是兩位數的除法練習》教學賞析

文 王焱烽

怎樣通過有深度的練習課教學設計，讓學生獲得對課堂學習內容的“深度理解”？受益于長三角四省市骨干教師交流研修項目，筆者在隨安徽省特級教師夏永立老師進行跟崗學習期間，夏老師以他傾心執教的《除數是兩位數的除法練習》一課為例，為我們揭示了學生的“深度理解”是怎樣煉成的奧秘。

一、以“選擇”始，深思運算方法，突破定勢

在一般的教學中，為形成除數是兩位數的除法運算技能，教師往往會在有限的課堂時間里，安排不同題型的、過量的計算題，以期達到“熟能生巧”的目標。然而學生在面對運算內容時——例如面對本節課的計算，相當一部分學生對題中數的特征不管不顧，頭腦中剩下的往往只是“筆算”的強思維定勢，對口算、簡算、估算這些運算方法往往意識不強。教師“由算至熟”的理念，遇上學生“以算代思”的認識，造成了運算枯燥、機械、淺表化學習的現實流弊。因此，夏老師借助課始簡約的練習材料，在引導學生對運算方法的選擇、定勢思維的突破中豐富運算學習的體驗。

【片斷1】看誰做得又對又快！

84÷6=90÷3=

900÷30=153÷22=

210÷30=800÷200=

90÷30=21÷3=

930÷50=210÷3=

1.引導觀察。

師：一定都要列豎式計算嗎？哪些題目不用列豎式計算？請你選擇：哪些只需要口算、哪些需要筆算？

生：153÷22 和930÷50 要列豎式計算。

生：84÷6 也要列豎式計算。

師：二年級時84÷6 需要筆算，現在只需要口算。可以口算的還有哪些？

2.組織整理。

師：哪些口算題目是有關聯的，我們把這些題目寫成一組。

課堂交流后，教師板書成兩組算式：

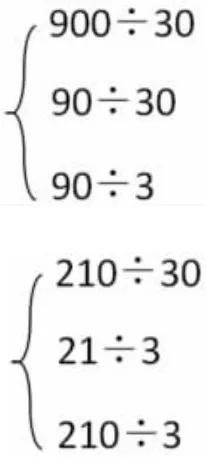
3.課堂交流。

師：哪些算式的商是一樣的，有什么變化的規律？

生：第一組中90÷3 的商等于30，把被除數乘10，除數也乘10，所以900÷30 的商也是30。

生：第二組中210÷30 的商是7，被除數和除數都除以10，所以21÷3 的商也是7。

師：為什么第一組中的90÷30的商不是30，是3 了呢？

生：因為被除數900 除以10，但除數30 沒有除以10，也就是沒有都除以相同的數。

師：讓你做900÷30，你可以想到哪道口算題？

生：9÷3。

師：還可以聯想到哪些題目？

生：900÷300=3。

生：9000÷3000=3。

……

除數是兩位數的除法運算，學生會把列豎式計算這一手段奉為圭臬。為打破學生“只會列豎式筆算”“以算代思”的狹隘認識，夏老師通過請學生選擇“口算”還是“筆算”，補上運算前“觀察”“審題”的理性選擇體驗，請學生進行“整理”和“交流”，加強運算時“尋求簡潔合理的運算途徑”過程性體驗，請學生開展“聯想”和“編題”，積累運算后“回顧”“總結”的反思性經驗。學生對觀察、聯想、運用“商不變性質”等“弱”刺激印象得以增強，“不能只是算”的思維定勢得以突破。學生對運算前、運算時、運算后“需要怎么做”的認識得以豐富。

二、由“問答”入，深究豎式算理，引發思辨

理想的運算教學，是幫助學生在理解算理的基礎上掌握算法。對算理的深刻理解，讓運算擁有了像根一樣能生長的力量。一般而言，教師在新授教學中，十分重視運算算理的理解，會通過畫圖、算式、小棒、計數器等多種方式引導學生理解算理。練習教學則著重以運算技能形成、思維方法感悟、解決簡單實際問題等為主展開。其實，練習課上，教師引導學生借助新授教學“練習”與“作業”中得到的知識經驗，對運算算理進行“再理解”。這樣的做法完全符合認知學習規律，也能收獲“溫故出新”的效果，為算法“再總結”，讓學習“再發生”。本節課從口算學習后轉入對列豎式計算的算理學習中，夏老師獨具特色的生—生“你問我答”，把豎式算理中隱含的“節點”“錯點”“盲點”顯露無遺。學生對“除數是兩位數的除法”算理有了深化理解。

【片斷2】誰能向他們提問？

師：觀察153÷22 的豎式（圖1），商是6，余數是21。誰能向她（生1）提問？

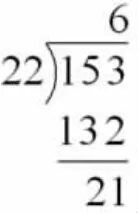
圖1

生：為什么6 要商在個位上？

生1：如果寫在十位上，6 就不代表6 個一。

師：被除數前兩位是15，比除數22 小，所以商是一位數。

生：余數21 代表什么？

生1：21 表示被除數153 減去商乘除數后得到的差。

生：豎式中的132 代表什么？

生1：是22 乘6 得到的。

生：為什么個位上商6 不是商7？

生1：把22 看成20，商7 就是7 個20，但實際上應該是22 乘7 是154，比被除數大。

師：也就是試商時要調商。還有誰要向她提問的？

……

師：觀察930÷50 的豎式（圖2），有誰要向他（生2）提問？

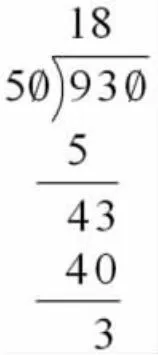
圖2

930÷50=18……30

生：既然商寫在了百位、十位上，為什么不是180，而是18 呢？

生2：如果是180，那么180乘50 的結果要比930 要大。

生：為什么要把被除數和除數末尾的0 同時劃掉？

生2：同時劃去，商還是不變的，能使計算變得簡便。

生：為什么余數寫的是3，橫式上寫的卻是30？

生2：豎式里余數是3，是在被除數的十位上，代表的是3 個十。

……

若非親歷課堂現場，很難相信10 多個充滿思辨味的高質量問題，一個緊接一個，從學生口中問答如流。陳省身指出，數學是自己思考的產物，首先要能夠思考起來，用自己的見解和別人的見解交換，才會有很好的效果。從學生之間“唇槍舌劍”般互問互答的課堂表現看，每一位提問者都將自己對豎式算理的理解，與回答者對算理的深入理解，進行“點對點”的精準交換———這種交換過程中的互相確認，為問答雙方和其他學生構建起向心力極強的思辨場——在這個思辨場中，大家對所問與所答的傾聽、思考、判斷、評價活動，讓算理的深度理解就此真實發生。這一有深度的“生問生答”環節設計，“將數學教學提升到高階思維層面，讓數學思維方式、方法在他們的內心深處扎根、生長，成為學習數學的自覺力量”。

三、借“改數”探，深研試商規律，開闊視野

一般而言，在結束對算理的思辨性交流后，教學會進入到諸如“列豎式計算”“改錯”“問題解決”等形式不一的基礎練習、變式練習等常規習題的“操練”環節，目的是為形成一定的運算技能。夏老師認為，在教學中，教師不能就題論題，而要適當進行拓展，只有找到習題潛在的智力因素，才能發揮最佳的課堂效益。在本節課中，如果僅僅是操練，學生所經歷的學習過程便缺失對數感、抽象能力、運算能力等的培育。《數學課程標準（2022年版）》在“運算能力”這一項核心素養表現性指標的表述是：能夠通過運算促進推理能力的發展。如何借助學生在運算練習中獲得的感性認識，引導學生對大量豎式運算后隱藏其中的試商規律進行理性思考，發展運算推理能力呢？在緊隨其后的練習環節，夏老師另辟蹊徑，將學生的思維帶入對豎式試商過程的分析及其規律總結中——

【片斷3】改除數，口算變筆算。

師：210÷30=7，想一想，把除數改成多少，這道題就需要筆算了？

學生答33、29、31、27、28 的均有。

師：你覺得除數改成多少，只需要一次試商，就能筆算？

板書：改題。

（學生答29、28、27、32、33 都有，也有學生說只有29）

師：請你自己列豎式驗證，是不是一次試商就行了？

生：28、29 都可以，只要一次試商就行。

生：27 也可以的，32、33 都不行。

師：210÷31，一次試商夠嗎？

生：需要兩次試商。

生：32、33。

生：超過30 的都不行。

師：想一想，除數是31 就要試商兩次，那么超過30 的，還要舉其他例子嗎？31 都不符合要求，比30 大的，更需要試商兩次。

師：如果是210÷26，要不要調商？請大家繼續驗證。

板書：猜想——驗證。

生：26 要調商，第一次試商7，太小了，調商為8，這樣第二次的商8 是合適的。

師：有時試商只要一次，有時試商需要兩次，試商小了，要調大，試商大了，要調小。

師：根據剛才的學習，你有沒有找到什么規律，在什么情況下，只要一次試商，什么情況下需要兩次試商？

生：我發現除數靠近7、8、9之類的，只要一次。靠近5、6 的，就要試商兩次。

生：因為靠近7、8、9，可以看成整十數，是把除數看大了。

……

怎樣為常規習題賦能，在開闊學生的學習視野中讓思維走向深刻？學生通過“一次試商”“兩次試商”的列豎式計算里，探索由除數變化引起試商次數變化的規律。更難能可貴的是，課堂上，許多學生一次次自發改除數、列豎式、試商調商，皆為“猜想——驗證”規律。把原本看似乏味的列豎式計算，變成有動力、愿努力、想盡力發現的主動探究活動——學生在愛數學的情感上與做數學的意識上可謂更進一步。這樣獨特的教學設計，也為“雙減”背景下的課堂練習與“數與運算”類作業改進設計與課堂指導，提供了可資借鑒的設計思路。

“練習課的質量取決于什么？在一定題量的基礎上，關鍵看思維的含量，看學生自主學習的積極性。”（華應龍）縱觀整節課，夏老師以簡約的學習材料，簡練的課堂語言，通過有深度的教學設計，讓學生充分經歷了運算方法的理性選擇、運算算理的深度理解、試商規律的深入探索過程。“深度理解”的課堂學習歷程，有效培養了學生良好的運算能力與主動探究習慣，體現了夏老師“比學生‘演練’更重要的是‘習得’，即獲得新的方法和思想，在學習能力上有新的提升”的練習課教學主張。顯然，在培育學生學科核心素養的背景下，以“深度課堂”理念上好上優練習課，夏永立老師這節練習教學的研究課起到了良好的示范作用。